考虑太阳帆板振动的空间绳系拖曳动力学与控制
2021-05-24姜泽华陈敏花
卢 山,姜泽华,刘 禹,陈敏花
(1. 上海航天控制技术研究所,上海 201109;2. 上海市空间智能控制技术重点实验室,上海 201109)
0 引 言
近些年来,空间碎片数量伴随着人类航天活动出现了快速持续的增长。据NASA最新数据显示,截止2019年12月19日已监测到20052个大型在轨运行目标,其中包括5376个有效载荷和14676个火箭箭体,而直径大于1 cm的碎片总数估计在百万量级,主要集中分布于高度在2000 km以下的近地轨道和地球同步轨道[1]。NASA科学家Kessler在1978年就指出,空间碎片之间的碰撞会产生更多的碎片,从而极大地增加潜在的碎片碰撞概率,并由此导致碎片数量呈指数级增长[2]。事实上,2009年2月10日发生的美国铱星33与俄罗斯宇宙号2251的卫星碰撞事件表明,空间碎片的碰撞连锁反应已经被触发了[3]。来自碎片的碰撞可能造成航天器不同程度的损伤和破坏,对人类航天活动的安全开始造成了极大的威胁[4]。相比于中小型空间碎片,大型空间碎片发生撞击的危害性更高,撞击产生的碎片也更多。大型空间碎片主要是指失效航天器,它们由于材料老化、器件失效、辐射损伤等原因而废弃在太空。与其他空间碎片不同的是,失效航天器往往保持着完整的卫星外形,并带有柔性附件如太阳帆板或天线。据统计,目前在轨运行着约2600个失效航天器。由于地球大气对于失效航天器的减缓效果十分有限,因此有必要采取主动方式清理失效航天器[5]。
失效航天器主动清除方式主要有电动力绳索降轨、机械臂抓捕、绳网捕获拖曳、太阳帆增阻和激光照射等[6]。其中,绳网拖曳概念因其重量轻、灵活性高和控制简单等优点,成为近几年最受学者关注的碎片清除技术之一[7]。典型的失效航天器绳网拖曳系统由三部分组成:具备机动能力的拖船航天器,待清除的失效航天器,连接目标和拖船的绳网结构。通过对拖船航天器实施轨道机动,可牵引失效航天器进入坟墓轨道或坠入大气层烧毁。
从绳系拖曳概念提出以来,各国学者对于失效航天器绳系拖曳系统的动力学和控制问题进行了较为广泛的研究[8-12]。文献[13]针对组合体沿系绳方向的振动控制问题提出一种时间最短以及能耗最小的最优控制策略,并进行了地面仿真试验,试验证明张力控制机构对张力指令具有很好的跟踪性能。Cho和McClamroch[14]提出了一种最优变轨技术,作用于拖船航天器上的连续推力以实现在两个圆轨道间的轨道转移。针对小的连续常值推力的化学推进绳系卫星系统,Sun等[15]基于欧拉-拉格朗日方法,采用哑铃构型建立了绳系拖拽系统的模型,将推进作用归一化为绳系卫星系统的推进系数,详尽分析推进系数对绳系卫星系统平衡点的影响,并利用分层滑模的设计方法设计了系绳张力控制律,实现了变轨过程中对面内摆角的抑制。Liu等[16]研究了GEO轨道上绳系拖曳离轨问题,将空间碎片和拖船航天器看作质点,考虑系绳断裂、拖船航天器与空间碎片碰撞和系绳缠绕等风险,着重研究了包含加速、平衡、旋转和返回的四阶段变轨策略。考虑空间碎片转动惯量、初始角速度和系绳长度的影响,Aslanov等[17]研究了通过系绳连接的空间碎片与拖船航天器组合体的动力学问题,结果表明,若拖船航天器推力的方向与系绳方向一致,且系绳保持张紧,那么离轨过程就是安全的。一般来说大气阻力的影响在轨道高度300 km以上可以忽略不计,若空间碎片相比拖船航天器有较大的横截面积,那么在拖船航天器拖曳碎片再入过程中,由于气动力作用空间碎片将快速减速,两者间可能会发生碰撞,在文献[18]中,Aslanov等设计了一种推力控制策略以避免碰撞。由于在网捕和拖曳过程中,碎片的旋转容易导致碎片与系绳发生缠绕的问题,文献[19]提出了一种自适应反演控制方法来保持碎片的姿态稳定。
以上诸研究在建立动力学模型时均未考虑失效航天器带有柔性附件的情况,而在拖曳过程中柔性附件产生的振动会对系统的稳定造成影响,且柔性附件可能断裂并产生更多更小的碎片。本文将对拖曳过程中太阳帆板等柔性附件振动对绳系组合体的拖曳过程的影响进行分析,并通过数值仿真的方式研究常值拉力控制下绳系拖曳系统的响应。
1 绳系拖曳系统动力学建模
绳系拖曳离轨的一般过程为:拖船航天器发射飞网捕获失效航天器后,通过拖船航天器的轨道机动拖曳失效航天器进入坟墓轨道。拖曳过程中由安装在拖船航天器上的系绳收放装置提供抑制失效航天器姿态章动的系绳张力,对于带有自旋的失效航天器,采取在绳结点处安装万向节的方式消除目标自旋导致的系绳扭转对拖曳过程的影响。
对携带柔性帆板的失效航天器进行拖曳移除是比传统刚体航天器的移除更为复杂的任务。帆板和系绳的振动,使得系统很有可能出现不稳定振动,因此对该系统的动力学建模和分析尤为重要。本节采用凯恩方法[20]对携带两个对称柔性帆板的失效航天器绳系拖曳系统进行动力学建模。由于飞网包裹住失效航天器后,将会钩挂在失效航天器本体外侧突出的大型太阳帆板上,因此在建模中将绳网简化为“四绳模型”,即系绳在绳结点处分叉成四根系绳连接在失效航天器两个对称安装的太阳帆板的四个角点上,实现对整个碎片的可靠连接。凯恩方程又称为具有虚功率形式的达朗贝尔原理,由于其兼具牛顿欧拉法和达朗贝尔方法的优点并且适用于非完整约束系统,在多体挠性航天器动力学建模中应用广泛[21]。
1.1 建模思路及坐标系建立
绳系拖曳系统由拖船航天器,失效航天器和系绳三部分组成。其中拖船航天器视为纯刚体,失效航天器视为带有柔性附件的刚体,系绳视为无质量的弹簧阻尼结构,主绳从拖船航天器上释放伸出,在绳结处分叉为四根子绳,分别连接于目标帆板的角点上。连接于拖船一端的系绳称为主绳,连接于碎片一侧的则称为子绳,以下将拖船航天器简称为拖船,失效航天器简称为目标。
为描述整个带有失效航天器的绳系拖曳系统中各部分的相对运动和在惯性空间中的绝对运动,首先定义如下坐标系:
1) 惯性坐标系fe(oexeyeze),原点oe位于地球质心,方向固定在惯性空间中。
2) 轨道坐标系fo(ooxoyozo),原点oo位于绳系拖船系统的质心,zo轴由系统质心指向地心,xo轴在轨道平面内与zo轴垂直并指向卫星速度方向,yo轴与xo,zo轴满足右手定则。上述坐标系的表述可参见图1。

图1 绳系拖曳系统的轨道运动示意图Fig.1 A schematic diagram of the orbital motion of the tethered towing system
3)拖船的本体坐标系fb1(ob1xb1yb1zb1),原点ob1为拖船的质心,三个坐标轴分别沿拖船的惯性轴方向。
4)目标的本体坐标系fb2(ob2xb2yb2zb2),原点ob2为碎片的质心,三个坐标轴分别沿碎片的惯性轴方向。
5)帆板k的本体坐标系fak(oakxakyakzak),oak固定在帆板本体上,oak为帆板与目标本体连接线的中心(帆板厚度忽略不计),yak为帆板长边方向,zak为帆板横向,xak,yak和zak满足右手定则。上述坐标系的表述可参见图2。
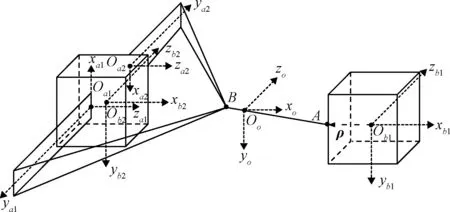
图2 绳系拖曳系统结构示意图Fig.2 A schematic diagram of the tethered towing system
拖船的质量为mb1,转动惯量为[Jx1,Jy1,Jz1], 目标中心体的质量为mb2,转动惯量为[Jx2,Jy2,Jz2]。帆板k的质量为mak,系绳分叉点B的质量为m3。系绳与拖船的连接点A在拖船本体系fb1(ob1xb1yb1zb1)的位置矢量为ρ,系绳与目标的帆板的连接点Bi在目标的帆板k的本体坐标系下的位置矢量为ρBi。拖船的姿态角表示为[φ1,θ1,ψ1], 是拖船本体系相对于轨道系fo的欧拉角,表示在拖船本体系fb1下。目标中心体的姿态角记为[φ2,θ2,ψ2], 是目标本体系相对于轨道系fo的欧拉角,表示在目标本体系fb2下。
1.2 系统的凯恩方程
对携带2个柔性附件的失效航天器的绳系拖曳系统,选取系统的广义坐标为:
(1)
式中:R1,R2和R3分别为oe到ob1,ob2和B的位置矢量在fe下的分量列阵,φb1和φb2分别是拖船和目标的本体系相对于惯性系的绝对转角在fb1和fb2下的分量列阵,qa1和qa2为柔性附件的前l阶模态坐标组成的l×1列阵,与时间有关。选取广义坐标的时间导数作为广义速率,并设置广义速率列阵为:
(2)

(3)
(4)
(5)
(6)
(7)
(8)
式中:上标“~”表示向量的叉乘矩阵,Ae,b1和Ae,b2分别表示拖船本体系和目标本体系到惯性系的转换矩阵,逆矩阵表示为Ab1,e和Ab2,e;Ae,ak表示第k个柔性附件的本体系到惯性系的转换矩阵,逆矩阵表示为Aak,e;Aak,b2表示目标本体系到第k个柔性附件本体系的转换矩阵,逆矩阵为Ab2,ak;Kak和Cak分别为失效航天器上柔性附件k的模态刚度阵和模态阻尼阵;rbak为柔性附件k未变形时Ob2到其安装位置Oak的位置矢量在fb2下的分量阵;QR1,QR2和QR3分别表示拖船,目标和系绳分叉点B所受的广义外力的合力矩阵,表示在惯性系下;Qωb1为拖船合外力对ob1的力矩列阵,表示在拖船本体系下;Qωb1为目标所受合外力对ob2的力矩列阵,表示在目标本体系下;Qak为对应于广义坐标qak的广义外力,表示在柔性附件k的本体系下。
1.3 系统的广义外力
拖船所受合外力在惯性系中的列阵表示为QR1,该合外力由拖船所受重力FG1,绳子的张力FlA,阻尼力FdA,和发动机拉力Ft组成,即:
QR1=FG1+FlA+FdA+Ft
(9)
目标所受合外力在惯性系中的列阵表示为QR2,该合外力由目标中心体和柔性附件所受重力合力FG2,绳子的张力FlBi和阻尼力FdBi组成,即:
(10)
式中:i为子绳的编号,其最大值为4。
绳节点B所受的合外力在惯性系中的列阵表示为QR3,即:
(11)
拖船所受的合外力矩在fb1中的列阵表示为Qωb1,该合外力矩由拖船所受重力梯度力矩MG1和系绳提供的力矩MA组成,即:
Qωb1=MG1+MA
(12)
目标所受的合外力矩在fb1中的列阵表示为Qωb1,该合外力矩由目标中心体和柔性附件所受重力梯度力矩MG2及系绳提供的力矩MBi组成,即:
(13)
对应于广义坐标qak的广义外力在fak中的列阵表示为Qak,它由作用在柔性附件k上的分布力Fqak和系绳与柔性附件的连接点Bi处柔性附件所受广义外力FBi组成,即:
(14)
1.4 系统的动力学方程
将第1.3节中描述的各广义外力代入方程(3)~(8)中,则获得整个带有太阳帆板的失效航天器绳系拖曳系统的完整动力学模型,该模型可表达为如下形式:
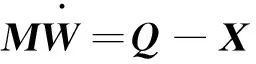
(15)
其中,
(16)
(17)
QT=[QR1,QR2,QR3,Qωb1,Qωb2,Qa1,Qa2]
(18)
(19)
2 稳定性分析
李雅普诺夫第一法的基本思路是通过系统状态方程的解来判别系统的稳定性。对于线性定常系统,只需解出特征方程的根即可作出稳定性判断。对于绳系拖曳系统这类非线性不很严重的系统,则可通过线性化处理,取其一次近似得到线性化方程,然后再根据其特征根来判断系统的稳定性。
由于系统整体运行于中高轨道,重力梯度力矩对拖船和目标姿态的影响相比于系绳张力引起的力矩是小量。因此在平衡状态分析阶段,考虑短时间内拖船和目标的姿态运动时,忽略重力梯度力矩对拖船和目标姿态造成的影响。
绳系拖曳系统中各广义坐标的平衡状态取值为θe1=0,φe1=0,ψe1=0;θe2=0,φe2=0,ψe2=0。在拖船无主动姿态控制时,为保证拖船姿态平衡,主绳与拖船的连接点须位于拖船质心位置,即ρ=0。同时忽略重力梯度力矩的影响,因此在平衡状态时拖船不受力矩的作用,其姿态运动为刚体运动形式,不存在振动状态,在线性化模型中予以省略。
平衡状态附近的系统广义坐标均表示为Γ=Γe+δΓ的形式,其中Γ是动力学系统中广义坐标和其一阶、二阶导数组成的列向量,Γe表示其在平衡位置的取值,δΓ则表征其偏离平衡位置的小量偏差。将以上各广义坐标及其一阶、二阶导数的表达式代入动力学方程(15)中,令l31=R1-R3,l31=R1-R3,δXT=[δl31δl32δφb2δqa1δqa2], 得到线性化的绳系拖曳系统系统动力学方程:
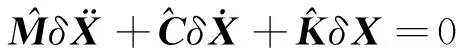
(20)

线性化后的带有失效航天器的绳系拖曳系统的特征方程表示如下:
(21)
其中,λ表示系统的特征根。特征根实部表示系统状态量长期变化趋势,其值为负说明相关系统状态量呈现收敛趋势,系统稳定。特征根的虚部表征系统参数的各阶振荡频率,特征根若为纯虚数则表征等幅振荡运动。根据广义坐标平衡状态取值,计算平衡状态附近的线性化模型,采用特征方程(21)求解系统的特征根,结果如表1所示。

表1 系统的特征根Table 1 The characteristic roots of the system
表1为系统5个状态量[δl31δl32δφb2δqa1δqa2]在空间3个方向的特征值,每个状态量在每个方向上各有1组2个特征根,故共求得15组30个特征根。特征根的实部为负数表示对应物理量衰减振荡趋势,实部为零,即特征根是纯虚数表征了等幅振荡运动。实部为正则说明对应物理量呈发散趋势,系统不稳定。本算例中系统状态量在系统轴向出现特征根为正,主要是由于该四绳分叉对称安装的绳系拖曳系统建模中忽略了各绳的扭转刚度,系绳无法提供沿系统轴向的扭转力矩对失效航天器沿系统轴向的姿态运动进行稳定控制。工程中采取在绳结点处安装万向节的方式消除系统轴向的姿态运动对拖曳过程的影响。
3 基于系绳张力的目标姿态控制
由于系绳尺寸相比于目标和拖船较大,所以可以将目标和拖船的姿态变化对系绳摆动的影响忽略,当拖船和目标相对位置不变时,可以近似认为系绳张力方向为恒定。据此,可以选取一个新的参考系,该参考系的坐标原点位于目标本体的质心上,z轴沿着目标与拖船的连线方向指向拖船,如图3所示。根据前面的假设,该坐标系的z轴指向与系绳张力方向相同。图中θ角为目标质心与绳结点连线和选取的参考系z轴间的夹角。

图3 参考系示意图Fig.3 A schematic diagram of the frame
在图3所示的坐标系中,观察目标在系绳张力作用下的姿态运动,实际上是观察目标相对于系绳方向的姿态运动。其优点为在拖船和目标相对方向基本不变时,可以不考虑系绳空间指向的影响,简化了分析过程。若在此基础上将系绳张力大小固定,则系绳张力对目标的影响可以等效为一个有势力的作用,张力在该参考系中所作的功只与绳结点在该参考系下的初末z轴位置有关。与此同时,在该参考系下张力的势能与目标的转动动能之和所代表的机械能是守恒的,也就是张力所做功会全部转化为目标的转动动能,即:
(22)


1) 当两星连线与目标自旋轴夹角θ≥θmax时,系绳张力为较大张力Tb。
2) 当两星连线与目标自旋轴夹角θ≤θmin时,系绳张力为较小张力Ts。

在工程应用中,常使用一种安装在主动星上的系绳收放装置来输出所需的系绳张力,由该装置实现张力的切换控制。目前该装置输出张力误差约为0.1 N,相比于选取的切换张力较小,可以满足控制要求。同时该装置响应速度较快,可根据姿态章动角的变化在较短时间内完成张力切换控制过程。此外,由于系绳始终保持张力,可能导致两星加速靠近发生碰撞的问题,提出采取系绳收放装置不断收放系绳,配合主动星推力器开机关机加速减速的协同控制来实现两星距离始终保持在一个安全的范围内的目标。
4 仿真校验
考虑仿真对象为绕本体主惯量轴自旋的携带柔性帆板的失效卫星,自旋角速度为5 (°)/s。采用第4节所述常值切换控制律抑制拖曳初始阶段失效卫星的姿态章动,选取切换张力为2 N和4 N,仿真结果如图4~9所示。

图4 失效卫星姿态角变化情况Fig.4 Change of attitude angle of invalid satellite

图5 失效卫星章动角变化情况Fig.5 Change of nutation angle of invalid satellite
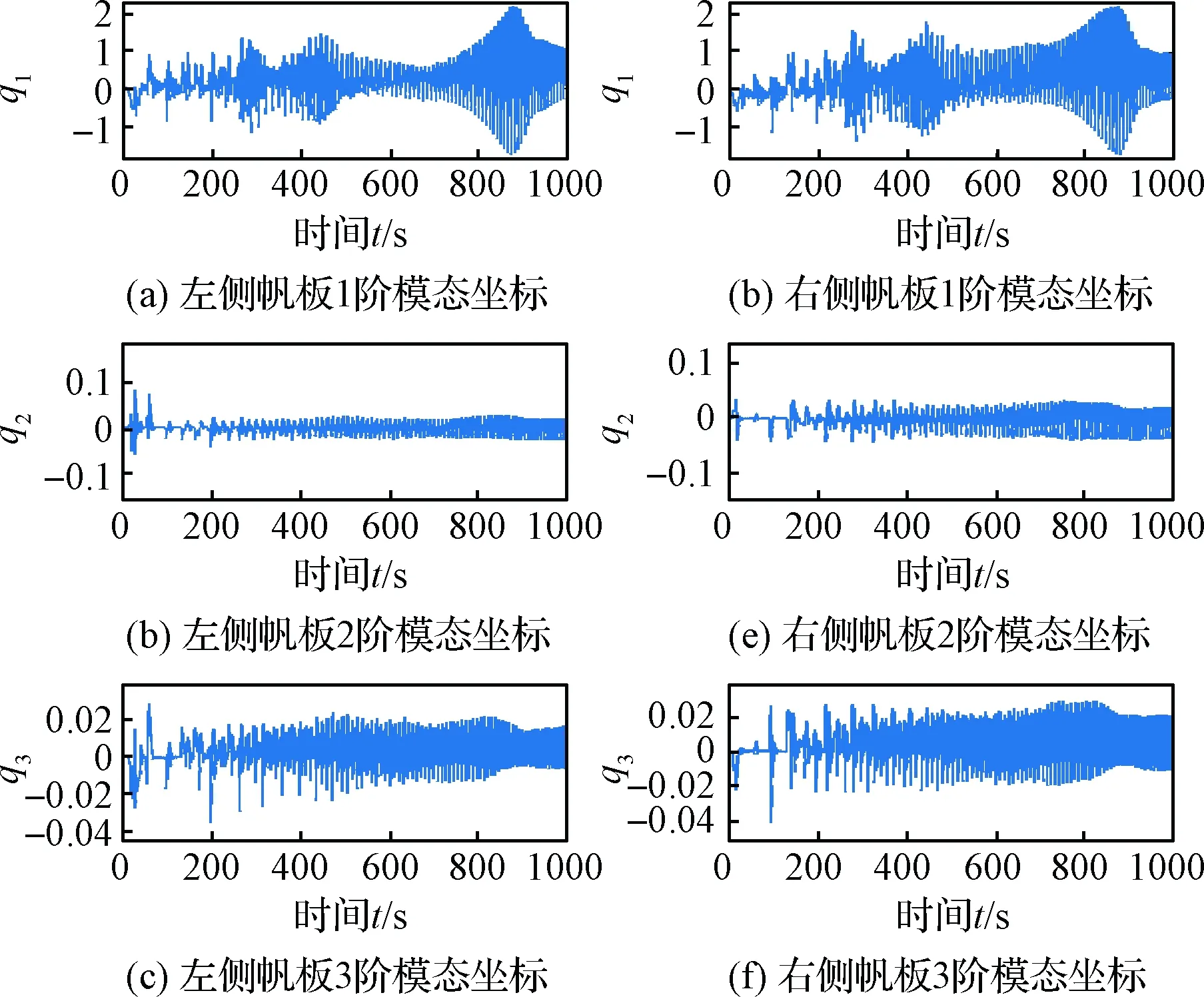
图6 帆板模态坐标变化情况Fig.6 Change of the model coordinates of the panels

图7 主绳张力变化情况Fig.7 Change in tension of main tether
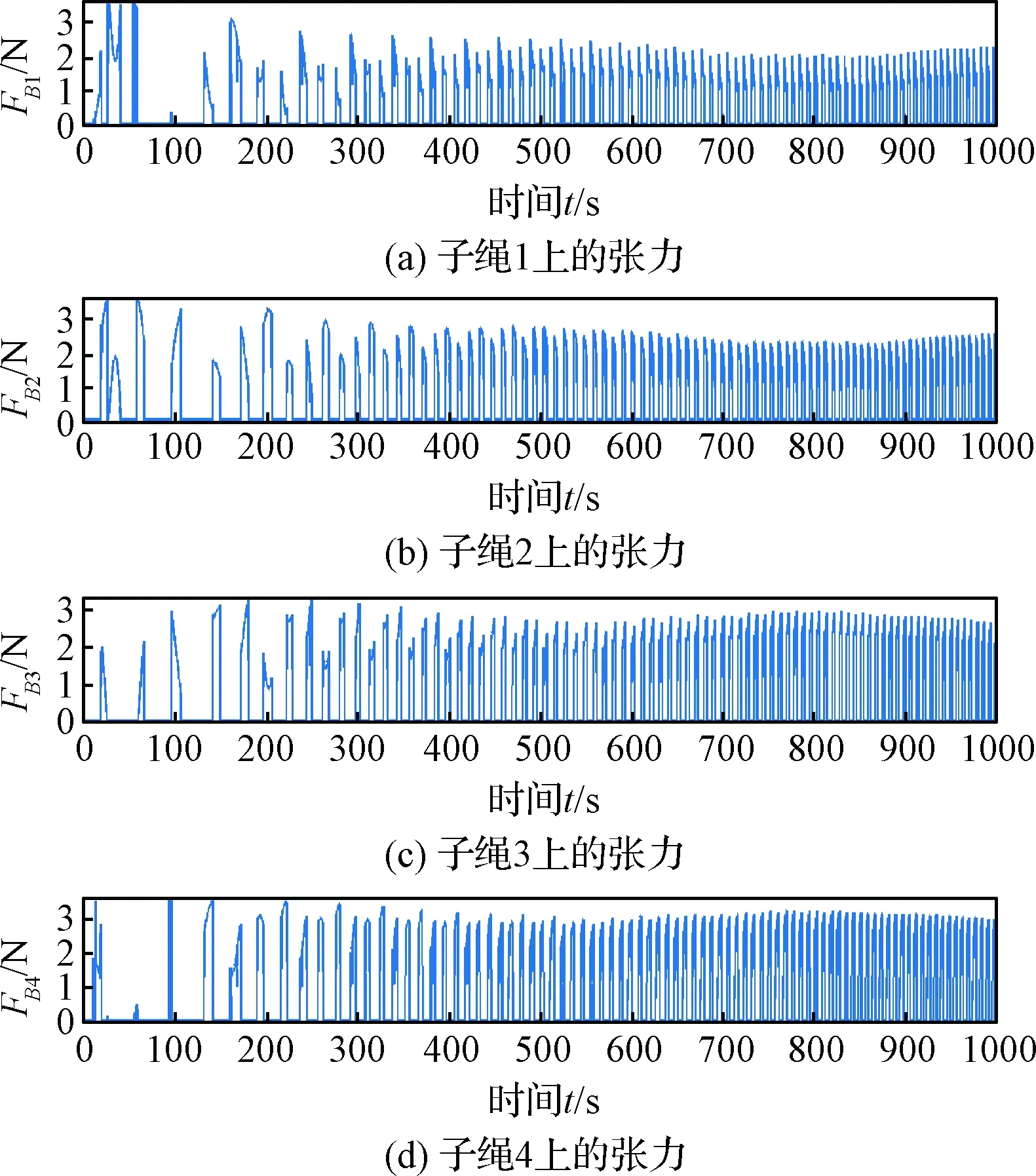
图8 四根子绳张力变化情况Fig.8 Change in tension of four sub-tether

图9 系绳长度变化情况Fig.5 Change of the length of the tether
在常值切换张力控制下,通过系绳收放装置输出主绳张力。由仿真结果可知,由于失效航天器具有绕本体自旋轴5 (°)/s的初始角速度,导致失效航天器在拖曳过程中的俯仰方向和偏航方向出现了大小不同的姿态角,通过切换张力控制,失效卫星的俯仰角和偏航角得到了有效镇定,而失效卫星的自旋角速度由于缺少该方向的控制力矩,一般采用在绳结点处安装万向节的方式消除目标自旋对拖曳过程的影响;在仿真模型中加入目标帆板挠性振动因素后,采用切换张力控制律,失效卫星章动角≤6°,控制目标为将章动角抑制在5°以内,目标帆板的小幅振动未对目标姿态造成明显影响。由于四根子绳绳长固定不可调节,失效卫星的姿态运动导致四根子绳的某几根出现松弛无张力的情况,如图9所示。本文中采用实时观测绳结点位置的方法判断子绳是否松弛,进而通过主绳张力实时解算每根子绳上的张力,如图8所示,使得系统具有真实的动力学特点。帆板的振动情况如图5所示,可以看出,帆板的振动在切换张力的时刻振幅增大,在无切换张力的时刻振幅在帆板阻尼影响下减小。由于不断进行张力切换控制,使得帆板始终存在小幅振动,由失效航天器姿态变化情况可以看出,帆板的小幅振动对绳系拖曳过程无明显影响,但对帆板自身结构的影响需结合帆板的材料、结构特性做进一步分析,考察是否可能发生帆板断裂的情况。
5 结 论
本文针对带有柔性附件的失效航天器的绳系拖曳离轨系统进行了动力学分析和控制方法研究。首先采用凯恩方法建立了完整的绳系拖曳系统轨道姿态动力学模型,该模型充分考虑了拖船航天器的姿态、系绳的质量、目标的姿态和柔性附件的振动;然后将非线性系统线性化后,求解了该线性化系统的特征根,通过李雅普诺夫方法对系统的稳定性进行了分析;之后针对目标可能产生的姿态章动设计了常值张力切换控制律;最后采用数值仿真的方式研究了失效航天器的绳系拖曳离轨过程,分析了帆板受力振动对拖曳过程稳定性的影响,校验了动力学模型的真实性和控制律的有效性,对采用绳系拖曳方式清除携带太阳帆板的失效航天器的空间碎片清除任务提供理论基础。
