基于配网量测数据的静态负荷模型参数辨识

杨坚，周正阳，于杰，沈一鸣，汪子晨，陈新建，洪骋怀

（1.国网台州供电公司，浙江 台州318000；2.国网浙江省电力有限公司，杭州310007；3.浙江大学 电气工程学院，杭州310027）

0 引言

电力系统负荷模型是电力系统分析、规划和控制的基础。随着社会经济水平的迅速提高、能源互联网技术［1］的广泛应用、智能配电网与微网［2］的建设、分布式可再生能源发电［3］的迅猛发展，负荷种类增加，复杂程度上升。相较于传统电力负荷，现代电力负荷的负荷特性已发生了很大变化，因此，有必要采用新原理和新技术，研究提高负荷建模准确度的方法。

文献［4］的静态负荷模型有较强的适用性，不仅能描述静态负荷特性，也能描述稳态下的动态负荷特性。文献［5］—文献［6］对于静态负荷的参数辨识工作着眼于基于短时采样数据的辨识，故只能反映在相应时刻附近的静态负荷特性，难以描述一日之内静态负荷特性的变化、获得日静态负荷模型参数，实现解析负荷中恒阻抗、恒电流、恒定功率（下称ZIP）成分的目的。

当前，我国大部分电网都安装了智能量测终端，实现了对专、公变用户用电信息的全采集，并配有配电网负荷管理系统［7］，对配电网数据进行有效记录和管理。目前，这些积累的大量配电网稳态量测数据已广泛应用于电网不同研究领域［8］，在配网运行可靠性分析［9］、配网短期、中长期负荷预测［10—11］等方面获得了丰硕的成果。

大量稳态数据同样成为近年来负荷特征分析及负荷参数辨识研究的热点。基于大量量测数据，通过聚类手段［12—13］，挖掘用户负荷的共同特性，针对不同负荷特性对负荷进行分类，进而对不同类型负荷建模，间接地提高了负荷模型的准确性。

本文基于配网量测数据，提出一种静态负荷参数的直接辨识方法，通过先聚类、后优化求解，获得了负荷全时段（96个时刻点）的静态电压模型参数，从而掌握各时间点负荷有功、无功功率随电压变化而变化的规律。

1 基于量测数据的静态负荷参数辨识方法

1.1 静态负荷模型

静态负荷模型包含幂函数模型、多项式模型以及幂函数与多项式混合模型等基本结构。由于一般情况下频率变化的幅度很小，可以忽略频率变化对负荷特性的影响，并且鉴于多项式负荷模型物理意义更为明确，即负荷由恒阻抗负荷、恒电流负荷、恒功率负荷等叠加而成，故电力系统仿真分析中静态负荷模型通常以多项式结构描述，即

式中：t为各时刻点；k为不同的负荷编号；分别为负荷有功功率、无功功率的额定值；为额定稳态电压；和分别为有功功率中恒阻抗、恒电流和恒功率负荷的ZIP系数；和分别为无功功率中恒阻抗、恒电流和恒功率负荷的ZIP系数，且有功与无功功率的ZIP系数满足：。

采用上述模型描述日负荷特性时，已知量测数据为各负荷96点实测有功、无功功率以及电压大小，而模型中各个时刻的功率初值及ZIP系数处于动态变化之中。此时，模型中的待求解参数多于方程个数，不能直接求解方程得到各时刻静态负荷的ZIP系数。

为了解决上述问题，本文提出以下假设：经过负荷曲线聚类后，具有类似负荷形态曲线的同一类负荷，在相同时刻的负荷ZIP成分比例相似，即在t时刻，属于同一类负荷的和参数相同。

考虑到稳态节点电压幅值接近于1，并计及上述假设，同类负荷第k条曲线在t时刻的量测功率主要取决于其额定稳态值。由于同类负荷的曲线相似，故可认为同类负荷中负荷曲线k的各点额定稳态功率由基准值与比例系数Pr,k决定，即

在上述假设下，静态负荷模型可描述为

通过优化拟合出该类负荷的96点静态负荷参数，并获得各时刻功率基准值Pt0和各负荷的比例系数Pr,k。

对日负荷量测数据进行预处理，并通过K-means算法对日负荷曲线进行聚类，得到同类负荷曲线，最后再使用优化算法辨识负荷参数，以下对这3个步骤进行详细展开。

1.2 日负荷曲线平滑化

实际量测数据不可避免地受量测误差和噪声的干扰，为了平抑干扰，需要对负荷曲线数据进行预处理。

具体地，对每一个用户的电压、负荷有功功率和无功功率，进行如下的平滑处理：

①对于第1、96个时刻，不处理。

②对于第2、95个时刻，处理如下

③对于第3—94个时刻，处理为

1.3 日负荷曲线聚类

基于1.1节的假设，同类负荷在同一时刻的ZIP系数可认为相同。因此，可采用聚类的方法，将专公变负荷进行分类。由于K-means算法是数据聚类的经典流行方法，该方法广泛应用与负荷的聚类分析［14—15］，故本文选择K-means算法进行负荷曲线聚类，具体步骤如下：①随机选择K个数据点作为初始聚类中心；②逐一计算N个数据点到K个聚类中心的欧氏距离，并将该数据点划入与其距离最小的聚类中心所在的类别；③划分完N个数据点后，分别计算K个类中数据点的平均值，作为这K个类新的聚类中心；④重复步骤2、3，直到K类的聚类中心都不再发生变化。

本文采用经典分类适确性（davies-bouldin index，DBI）指标确定最佳聚类数目。DBI值越小，类内距离越小，类间距离越大，分类效果越显著。DBI定义为

式中：K为聚类数目；ci、cj分别为第i类、第j类的聚类中心；分别为第i类、第j类中的数据点到相应类的聚类中心ci、cj的平均距离。

为了评价不同初始聚类中心对应的聚类结果，本文采用经典的误差平方和（sum of squared error，SSE）指标ISSE。首先设置聚类次数，再根据每次聚类结果计算相应的ISSE值，最终选择ISSE最小时的聚类结果。ISSE的计算公式为

式中：Ni为第i类中的数据点数量；nij为第i类中的第j个数据点。

根据上述2个指标，通过多次聚类即可取得负荷的最佳聚类结果。

1.4 多项式模型参数辨识方法

以上对专公变量测数据进行了数据预处理，并通过K-means聚类算法对负荷进行了分类，记此时某类负荷的负荷模型为

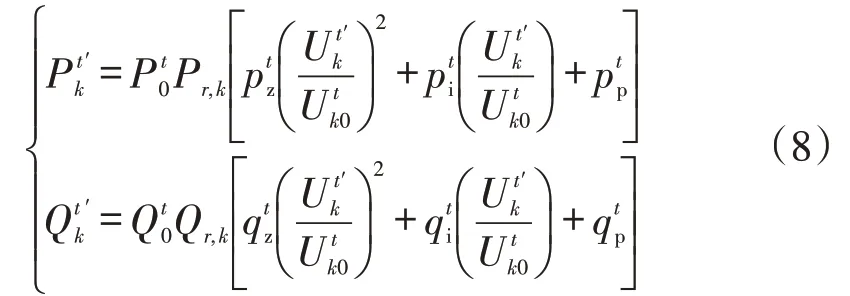
式中：t为各时刻点；k为该类负荷中各负荷曲线编号；和分别为平滑后的各点有功、无功和电压值。

基于1.1节的假设，可对同一类的日负荷曲线的参数进行统一辨识。待辨识的N个数据最佳参数值应使得同类负荷各时刻点的负荷功率计算值的误差平方和最小，故以此为参数辨识优化模型的目标函数。具体地，静态有功模型参数辨识优化模型的目标函数为与相应量测值

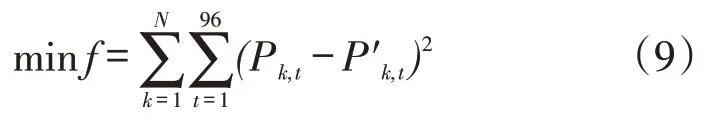
约束条件为

静态无功模型参数的辨识与有功的相似，其辨识优化模型也与式（9）和式（10）类似，此处不再赘述。

对上述优化模型，由其结果可得到该类多项式模型的参数。综上，基于配网量测数据的日静态负荷模型参数辨识的流程图如图1所示。

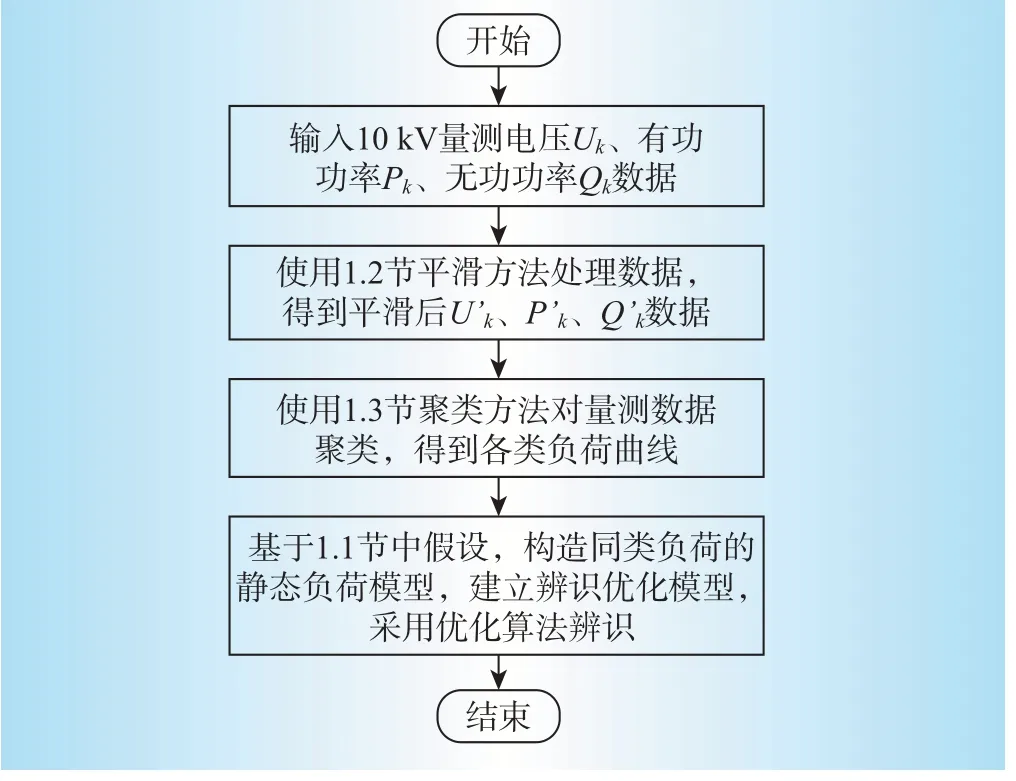
图1 静态负荷参数辨识流程Fig.1 Static load parameter identification process

2 算例分析

2.1 算例说明

以有功负荷的ZIP系数为例，分析上述参数辨识方法。

首先将专、公变有功功率量测数据聚类，得到工业、民用等几类典型负荷曲线，取某类负荷曲线对应的电压量测曲线Uk，将其作为构造算例使用的电压值。

取某类负荷的聚类中心曲线作为构造有功曲线的额定稳态值P0的基准值，如图2所示。第一类为典型的工商业负荷曲线，第二类则是民用负荷曲线。构造曲线的额定稳态值比例Pr,k取为负荷量测功率Pk在基准值曲线上的投影。

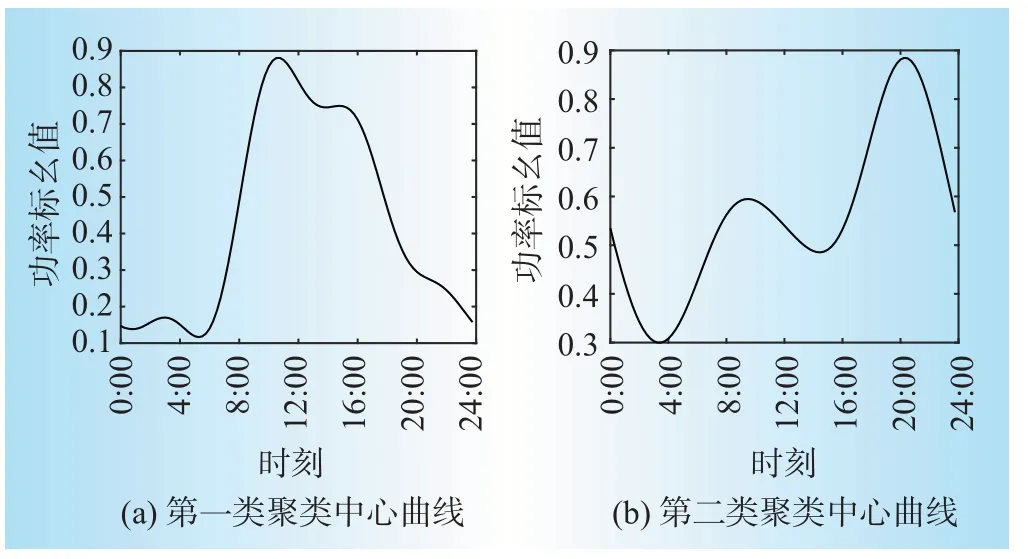
图2 聚类中心曲线Fig.2 Cluster center curves

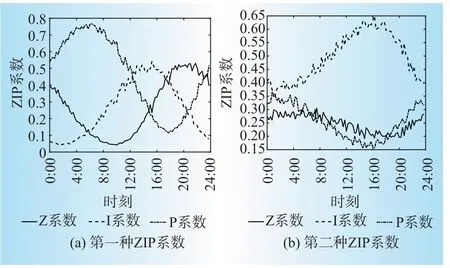
图3 构造有功ZIP系数Fig.3 Constructed ZIP parameters of active power

对以上2类不同电压，构造2种不同的有功ZIP系数，作为辨识结果的参考，如下图3所示。2种ZIP系数分别描述了2类负荷有功功率的时变静态电压特性，在各时间点上的Z、I、P系数不同，其中，第一种的Z、I和P系数在不同时间点上取得最大值和最小值，第二种的I系数较高，Z、P系数较低。所构造的2种算例的目的是能较全面地测试所提算法对较高和较低Z、I、P系数的辨识效果。

结合构造的ZIP数据、实测电压数据以及构造的额定稳态有功功率，通过静态负荷数学模型方程，得到2组相似的96点功率曲线，以此作为2个静态负荷参数辨识算例的输入功率数据，2类负荷特性曲线分别对应2类电力系统典型负荷。

2.2 静态负荷有功系数辨识

基于2.1节的2个算例有功和电压数据，采用本文所提方法辨识对应的静态有功负荷ZIP系数，并与2.1节中已知的2种ZIP系数做对比，结果如图4所示。由图可见，2个算例辨识出的ZIP系数与实际ZIP系数基本一致，验证了96点静态负荷系数辨识结果的正确性，直观地说明了所提辨识算法具有可行性，且具有较高的准确度。

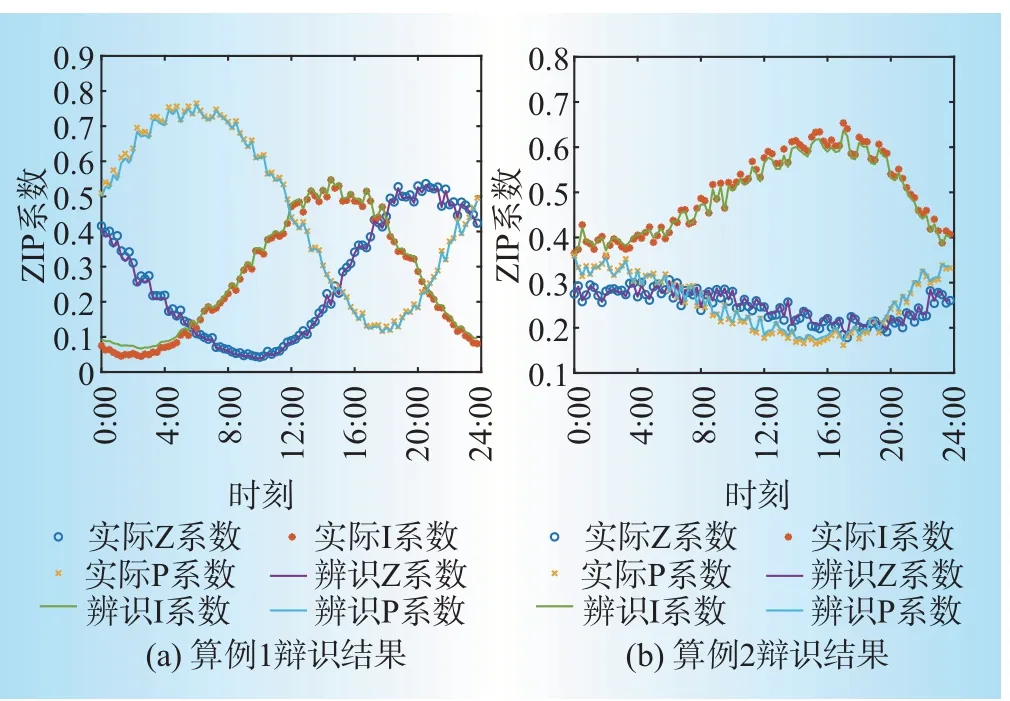
图4 辨识结果Fig.4 Identification results

为了进一步评估辨识结果的准确度，定义辨识系数与实际系数的误差平方和ISSE、各ZIP系数的平均相对误差εˉ以及最大相对误差εmax等3个指标如下

式中：pz,t、pi,t和pp,t分别为实际第t点恒阻抗、恒电流和恒功率负荷的有功功率系数；p′z,t、pi,t和pp,t分别为辨识得到的第t点恒阻抗、恒电流和恒功率负荷的有功功率系数负荷系数；εˉz和εz,max分别为Z系数的平均、最大相对误差，I和P的计算与其相同。

算例1误差平方和为0.28%，算例2误差平方和为0.648%，因此，从整体情况看，辨识结果与实际值的拟合程度高。表1给出了本节辨识结果的相对误差。平均误差及最大误差说明ZIP 3种系数各自的辨识效果较好。

表1 系数辨识结果分析Table 1 Analysis of parameter identification results

图5显示了两算例中，各时刻I系数与相对误差的关系。由图5可见，算例1的最大相对误差出现在I系数最小时。为了避免在I系数较小时辨识结果相对误差较大，从而影响对辨识准确度的判断，在算例2中设置I系数大于Z、P系数，但I系数平均相对误差和最大相对误差依旧大于Z、P系数。因此，可认为I系数的辨识难度大于Z、P系数。

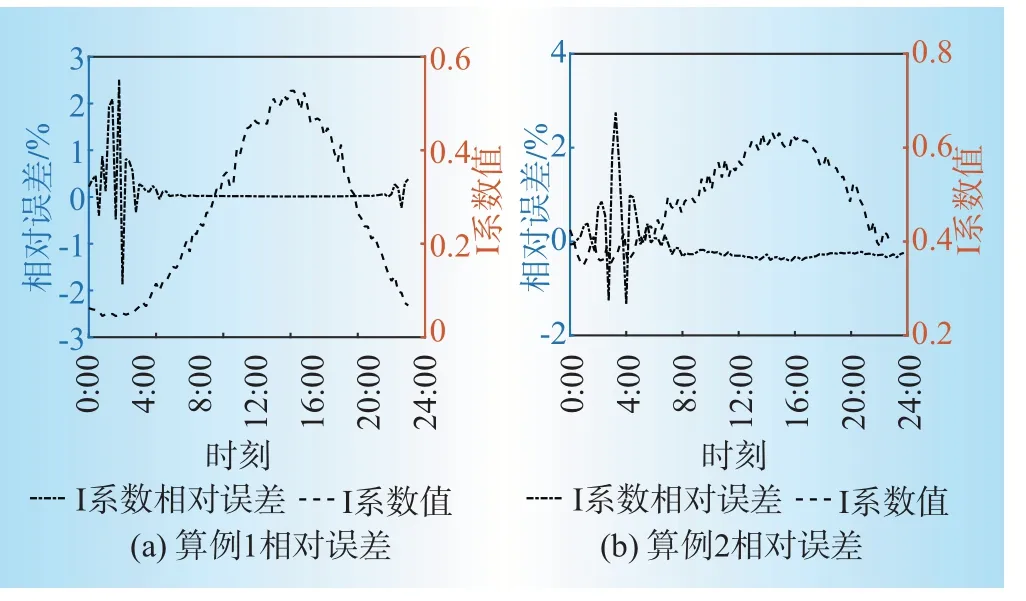
图5 恒电流系数相对误差与实际值的关系Fig.5 Relationship between relative error and actual value of constant current parameter

2.3 辨识算法的鲁棒性

在所提负荷参数辨识方法中，假设了同类负荷在同一时刻具有相同的静态ZIP系数，但显然在实际情况下，各专、公变下的负荷模型ZIP系数难以完全相同。

为此，假设2类负荷的基准ZIP系数如2.1节所述，各负荷实际ZIP系数与基准的偏差满足以0为期望、σ为方差的正态分布。然后，应用本文所提算法，辨识基准ZIP系数。

图6显示了以算例1为基础，当σ等于0.01时的辨识结果。这时，辨识系数的误差平方和等于0.1，辨识所得ZIP系数与基准值基本一致，但I系数已在0:00—4:00时段出现了较大误差，最大误差为0.042 6。

图7进一步显示了σ增加至0.02时的辨识结果。这时，辨识误差平方和约0.5，辨识所得ZIP系数的变化趋势与基准值符合，但在16:00—24:00时段出现较大误差，最大误差仍对应于恒电流系数，其为0.135 2。

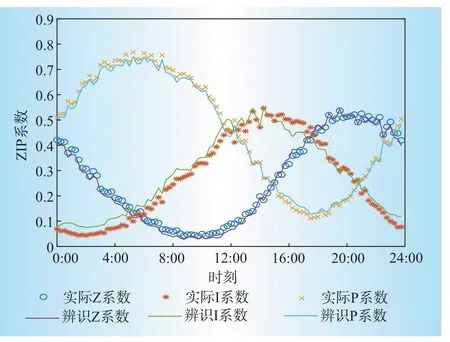
图6 辨识结果（σ=0.01）Fig.6 Identification results（σ=0.01）

图7 辨识结果（σ=0.02）Fig.7 Identification results（σ=0.02）

进一步，连续改变σ，两算例辨识误差平方和的变化趋势如图8所示。由图8可见，2类曲线的辨识误差随着σ增大而增大，辨识结果与实际基准值之间的误差平方和逐渐增大，表示辨识结果与基准之间误差逐渐增加。但从图6、图7可见，虽然辨识结果出现误差，但辨识结果依然可以反应负荷ZIP成分的时变规律。

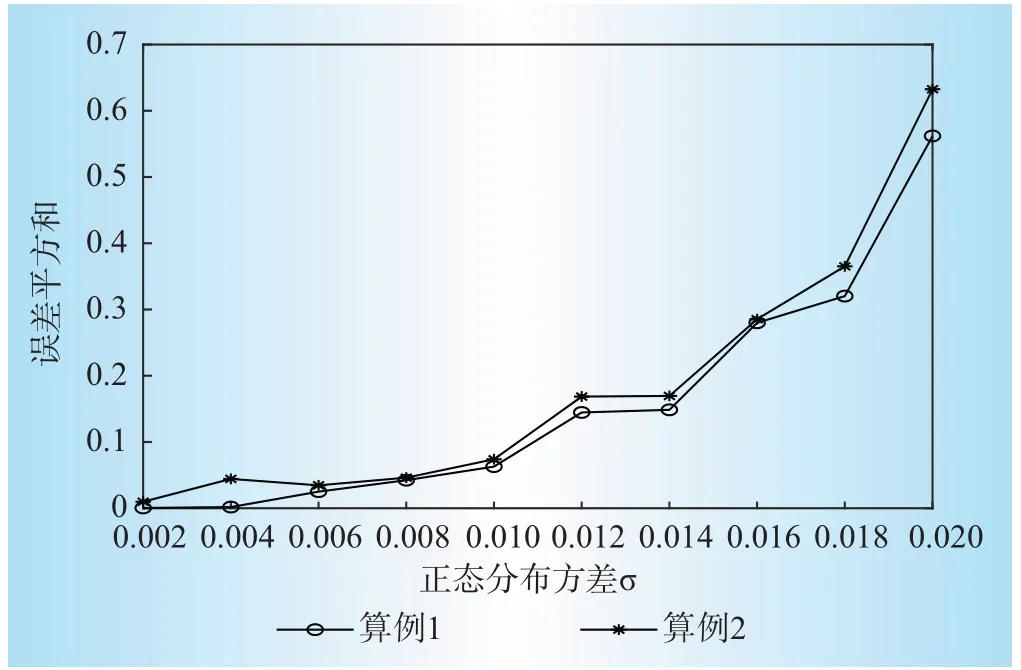
图8 辨识误差与方差的关系Fig.8 Relationship between identification error and variance

2.4 相邻点变化大小对辨识结果的影响

实际上，负荷具有时变性的特点，在量测的15 min时间间隔内也可能发生负荷ZIP成分的较大突变，需要考虑相邻点负荷成分变化大小对辨识结果的影响。

考虑一种极端的变化方式，即在96点中任意2个相邻点之间的负荷ZIP成分都发生突变，且最大突变值相同。当在2.1节算例基础上，相邻时刻最大变化为0.2时，对应的辨识结果如下图9所示，此时负荷ZIP系数有较大变化，辨识结果与实际ZIP系数基本一致，辨识效果较好。

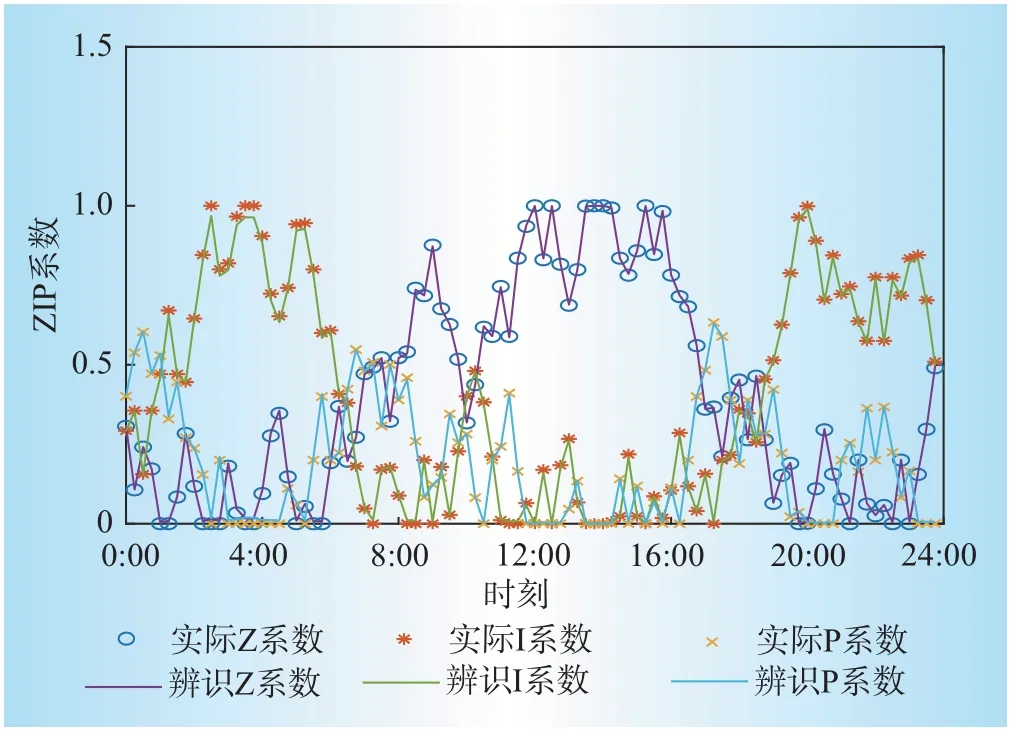
图9 最大变化0.2时辨识结果Fig.9 Identification results when maximum variation is 0.2

逐步增大相邻点的ZIP系数变化，计算辨识结果与实际值的误差，结果如图10所示。随着各相邻点之间负荷成分变化大小的增加，辨识系数的误差平方和增大，而当ZIP系数最大变化值为0.5时，辨识结果的误差平方和为0.02，整体上看误差并不显著。考虑负荷在15 min中变化、即其ZIP系数变化不会过于极端，故可认为所提辨识算法能适应ZIP系数较快变化下的辨识问题。

图10 变化值与辨识误差关系Fig.10 Relationship between the variation and identification error

3 结束语

针对静态负荷模型参数辨识问题，基于配网量测装置采集的负荷节点电压、有功和无功负荷功率稳态量测数据，提出了一种基于数学优化的静态负荷参数辨识方法。理论分析表明，该方法可以辨识静态负荷模型的有功、无功负荷ZIP系数，实现解析负荷成分的目的；算例分析表明，该方法具有较好的准确性，可以准确辨识静态负荷模型ZIP系数。