住宅小区充电站电动汽车有序充电方法

2021-05-23李敬航杨德玲赖伟坚林泽宏张世斌李捷管维灵

电力需求侧管理 2021年3期

李敬航，杨德玲，赖伟坚，林泽宏，张世斌，李捷，管维灵

（1.广东电网有限责任公司东莞供电局，广东东莞523000；2.苏州华天国科电力科技有限公司，江苏苏州215000）

0 引言

电力作为国家发展的基础保障，其需求随着新能源的开发和电力政策改革的深化发生了深刻的变化。电动汽车（electric vehicle，EV）作为配电网中渗透率较高的一种新型可调负荷，受到了人们越来越多的关注。

EV的可调特性主要体现在其电池的充放电过程，将入网EV的充电时间由用电高峰期转移至低峰期，即可实现EV的有序充电，对于电网运行成本的降低以及负荷的“削峰填谷”具有一定的作用。但EV的负荷特性具有较大的时空不确定性，如何对充满随机性的EV进行有序充电的优化，成为了目前电力行业亟待解决的工作难题。目前已有众多文献对EV的有序充电进行了研究。文献［1］建立了EV充电与清洁能源协同的时空模型并提出有序充电策略，但不能满足充满不确定性的实际工程应用。文献［2］基于电网在线运行状态监测系统进行数据的采集，采用竞争深度Q网络结构，对EV充电进行优化控制。文献［3］建立EV有序充电的多目标模型，并提出一种基于改进鸡群算法的有序充电策略。文献［4］利用EV作为分布式储能时所具有的灵活性和可调节性，引入EV群管理机构，提高对EV充放电管理的便捷性。

利用先进的数据挖掘技术对EV的充放电进行优化，文献［5］对数据进行挖掘，并采用K-means聚类对数据进一步处理，对EV有序充电具有指导意义。文献［6］基于数据挖掘技术和K-means聚类算法，提出了EV用户细分方法和价值评价方法，为运维和策略制定提供有效依据。文献［7］利用K-means聚类方法，通过对车主行为和充电时间分析，总结了EV用户的行为特征。

因此，本文结合时下电力系统特点，基于先进数据挖掘技术首先建立起EV的数学模型，以北京市某住宅小区的EV出行历史数据为例，利用模糊C均值聚类算法对车主的行驶行为、入网EV的初始电池荷电状态进行分析。把握EV负荷特性，基于马尔科夫链的思想建立由精炼后的多条典型EV负荷模式转移概率矩阵组成的模型，对EV的随机动态变化过程进行描述，并应用多种群遗传算法求解住宅小区内EV的有序充电问题。

1 电动汽车模型建立

当EV随机接入系统后，若EV充电站能将一定区域内的EV统一管理，当EV接入充电桩后获得该车的数据，即荷电状态SOC，期望离开时间tleave，结合所有站内EV的数据对每台EV充电功率进行分配，进行有序的充电调度。在满足用户的需求前提下，将一部分充电负荷转移至用电低峰期，即可实现EV的有序充电。

假设EV于tin接入电网便以最大功率直接进行充电，充满所需时间tdismin，若车主设定的离开时间tleave>tin+tdismin则视该EV为可调EV，可对该EV的充电时间进行调整，从而实现有序充电。单台EV的模型表示为

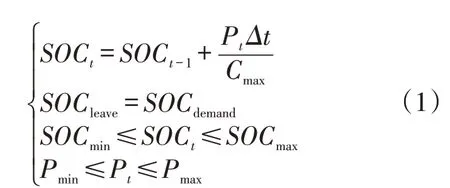
式中：SOCt为电池t时段的荷电状态；Cmax为电池容量；SOCmin、SOCmax分别为荷电状态的最小值、最大值；SOCleave、SOCdemand分别为EV离开电网时荷电状态及用户的需求值；Pt为t时段的充电功率；Pmin、Pmax分别为充电功率的最小值、最大值。

2 EV负荷特性分类方法

对EV负荷特性进行分类，一般使用聚类分析法，对EV车主行驶行为与充电特性根据一定的准则划分，使得划分到同一类型中的用户最大程度地具有相似或接近的负荷特性，并且不同类型的负荷特性具有较大的差异性和区别显著的特征。

模糊C均值聚类算法对EV特性数据进行聚类，可以得到相对更为科学、合理的划分结果。首先随机选取若干EV负荷特性数据的样本作为初始聚类中心，并赋予所有样本对各个聚类中心数值一定的隶属度。该算法的目标函数J为所有数据点到各个聚类中心的距离与隶属度的加权总和，然后迭代上述过程，反复修正聚类中心，其修正过程如式（3）所示，即

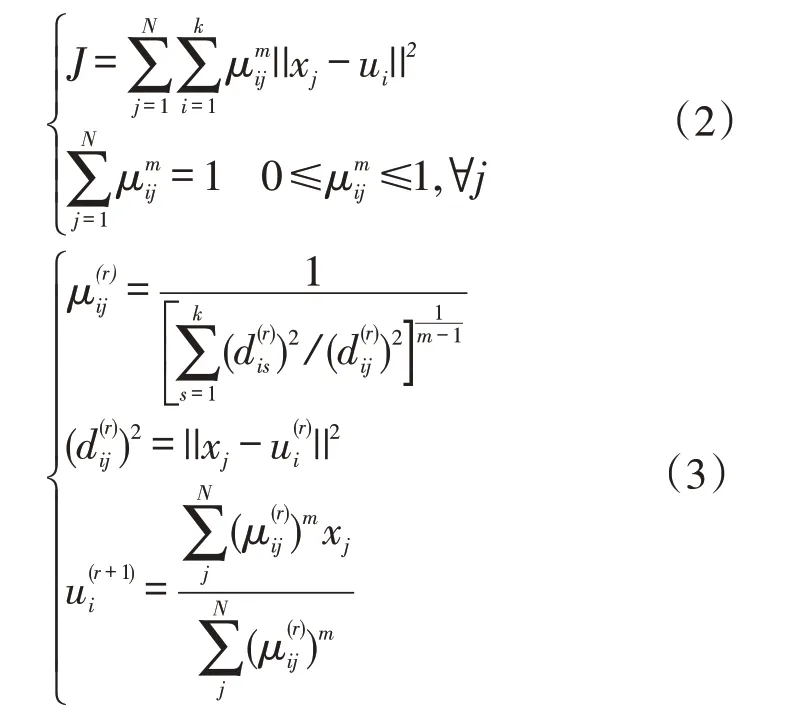
式中：N为EV负荷的数据样本数量；k为聚类数目；xj为第j个EV负荷的样本；ui为第i类EV数据样本的聚类中心；为ui的第r次迭代；为第j个样本属于第i类簇的隶属度；r为算法当前迭代次数；为第r次迭代第j个样本属于第i类簇的隶属度；m为模糊系数，通常取m=2；为第j个EV数据样本在第r次迭代后，计算得到的与第i类EV数据样本的聚类中心的距离。

算法过程描述如下：

（1）确定聚类数目k，从EV样本数据集中随机选取k个样本，并将其作为初始EV特性类别的聚类中心；

（2）完成每个EV特性类别的聚类中心的初始化后，根据式（2）和式（3）计算距离和隶属度；

（3）计算第i个EV特性类别的聚类中心；

（4）设定阈值ε，反复更新J(r+1)，若有J(r+1)-J(r)<ε，则终止迭代过程。

以北京市某住宅区的EV出行数据为样本，随机选取500台电动汽车进行分析，利用上述方法进行聚类，得到其充电开始时间、充电持续时间、初始荷电状态的三维聚类结果如图1。得到2个聚类中心分别为（8.75，2.2，0.5），（17.2，2.2，0.5），且上午的充电开始时间服从正态分布，下午的充电开始时间服从柯西分布；充电持续时间和初始荷电状态都服从正态分布。

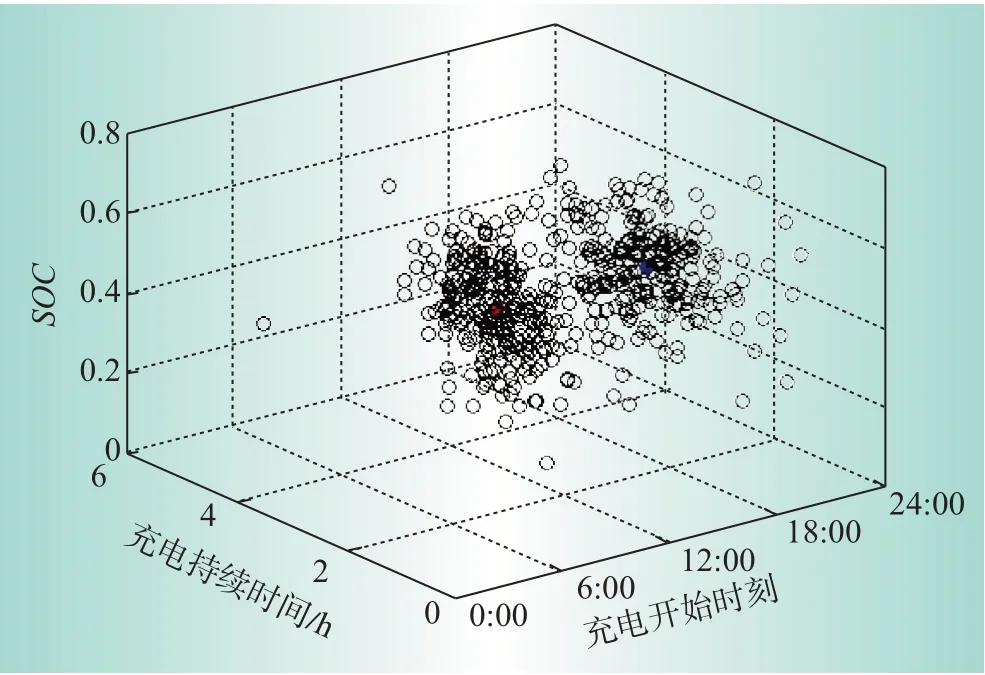
图1 模糊C均值算法聚类结果Fig.1 Clustering results of fuzzy C-means algorithm

3 基于马尔科夫链的电动汽车模式转移模型

在描述随机过程中，马尔科夫链（Markov chain，MC）是一种十分常见的工具。

同一EV在不同日的EV充电曲线可以看作不同模式下的EV充电负荷在动态变化，当日的EV充电模式仅与前一天的EV充电模式有关，与之前的EV充电模式无关。因此将EV的充电负荷变化过程近似于马尔科夫链，建立由精炼后的多条典型EV充电曲线和EV负荷模式的转移概率矩阵组成的模型，对EV随机动态变化过程进行描述。

模糊C均值聚类算法能够有效地将形状相近或距离紧密的EV充电负荷曲线划分成一类，进而形成若干类差异性较大的EV充电负荷类别，以此作为EV充电负荷模式划分的依据。

对每台EV以每天15 min的间隔采样一次，其功率采样点序列即为EV日充电负荷曲线，即

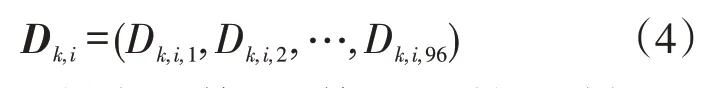
式中：Dk,i,j为EV样本xk第i天第j个采样时刻的功率值，j取1，2，…，96。

EV日充电负荷曲线样本进行标幺化处理，即

式中：Dk,i_Max为EV日充电负荷曲线样本的最大值。

对标幺化后的每台EV的Nk条标幺化充电负荷曲线进行模式划分，采用模糊C均值聚类算法进行聚类分析，ck为聚类数目，则聚类目标函数为

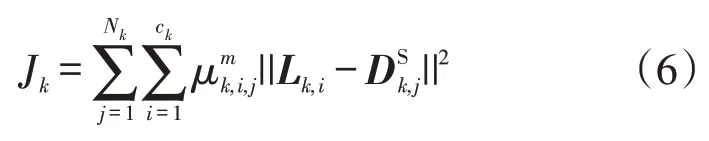
并由此设定用户xk被分类为第i个模糊类时的EV充电负荷模式为Mk,i，并以EV充电负荷聚类中心曲线Lk,i对EV充电负荷模式Mk,i进行表征。

完成对EV充电负荷的模式划分后，根据对历史EV日充电负荷曲线的划分结果，在认为EV充电负荷模式转移过程为齐次马尔科夫链的假设基础上，对xk的EV充电负荷模式转移过程进行具体分析。

用户xk充电模式Mk,r到Mk,l的一步转移概率为

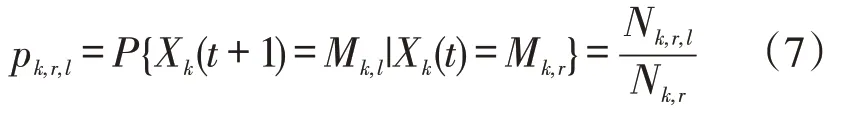
式中：Xk(t)为用户xk第t天所处的充电负荷模式；Nk,r,l为用户xk从充电模式Mk,r转移到Mk,l的频数；Nk,r为xk处于充电模式Mk,r的天数。

用户xk处于充电模式Mk,r的概率为

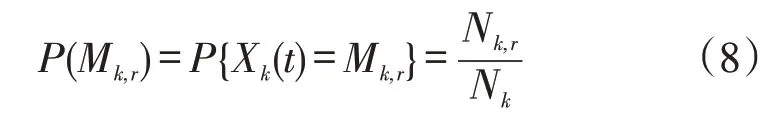
用户xk从充电模式Mk,r一步转出的概率为

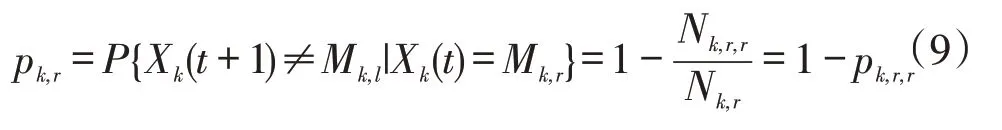
式中：Nk,r,r为用户xk从充电模式Mk,r仍转移到充电模式Mk,r的频数；pk,r,r为xk从处于充电模式Mk,r仍转移到充电模式Mk,r的一步转移概率。

4 EV有序充电求解

4.1 目标函数

将住宅小区内的运行成本最低作为目标函数，即

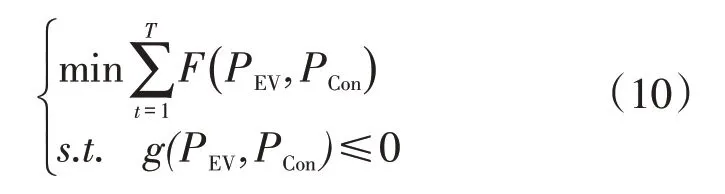
式中：PEV、PCon分别为EV和常规负荷的功率；F(PEV,PCon)为与PEV、PCon相关的运行成本；g(PEV,PCon)为相关约束条件，包括EV的充电功率约束和常规负荷约束、变压器容量约束等。

4.2 多种群遗传算法

针对EV的有序充电优化问题，采用多种群遗传算法（multiple population GA，MPGA）进行求解，MPGA针对标准遗传算法的早熟现象进行了改进。EV有序充电优化中，决策方案数目随着接入EV数目的增多而呈指数型增长，使用性能良好的MPGA算法能够在有限的算力和时间内通过种群的进化过程完成寻优，得到令人满意的结果。

设置交叉重组概率在［0.7，0.9］内随机产生，变异概率在［0.001，0.05］内随机产生，最优个体最少保持代数MAXGEN取值为10~15。

5 算例分析

5.1 基本参数

本文采用某居民住宅小区进行算例仿真，该小区除EV之外的常规负荷如图2所示，小区的常规负荷峰值可达3 500 kW，最低负荷为2 345 kW；假设该小区共有500辆电动汽车，小区充电站内有100台充电桩，充电桩的额定充电功率为10 kW；优化时间为24 h，以每15 min为一个断面，从早上8:00到次日早上8:00共96个时段。在matlab2018a的环境下进行编程，用MPGA进行求解。

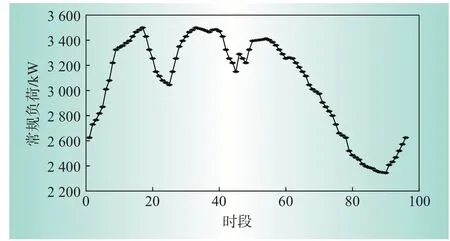
图2 常规负荷图Fig.2 The diagram of conventional load

5.2 算例分析

5.2.1 有序充电和无序充电的结果对比

图3和表1为无序充电和有序充电的优化结果对比。可以看出，所提出的有序充电优化方法对于改善系统运行情况有一定的积极作用。无序充电时大量的EV充电时间集中在中午和晚上2个高峰，与常规负荷叠加，产生“峰上加峰”的现象，影响变压器的安全运行。采用本文方法后，绝大部分充电负荷被转移到谷时段。运行成本从8.52万元降低到了7.45万元，降低了12%以上；最大峰谷差从1 587.2 kW降低到1 039.1 kW，降低了34%以上。

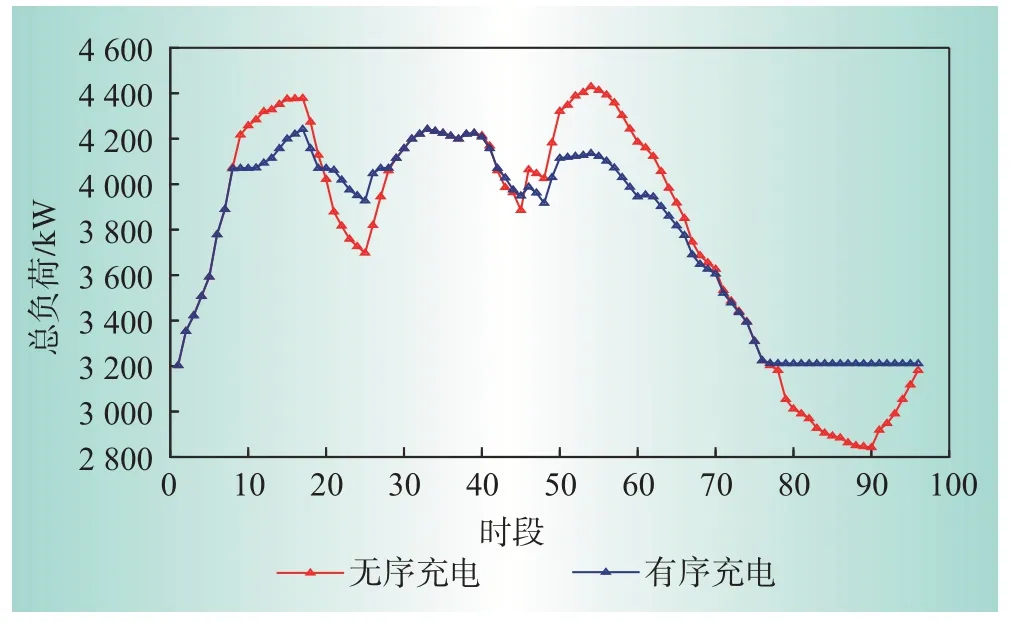
图3 总负荷曲线对比图Fig.3 Comparison of total load curves

表1 无序充电和有序充电结果对比Table 1 The comparison result of orderly charging and disorderly charging

5.2.2 不同EV渗透率下的结果对比

图4给出了该小区采用本文的方法进行有序充电、在不同EV渗透率下的总负荷曲线对比图。可以看出随着EV渗透率的增大，充电站能对更多的充电负荷进行调控，更多EV的充电负荷都由用电高峰期转移到了用电低谷期，对于降低运行成本和“削峰填谷”的作用越明显。

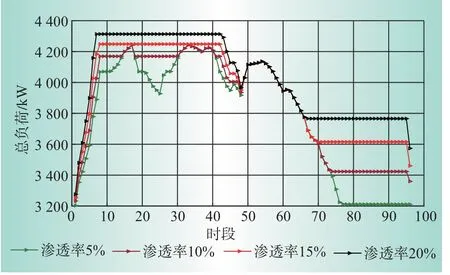
图4 不同EV渗透率下的负荷曲线对比Fig.4 Comparison of load curves under different EV permeability

为进一步挖掘住宅小区充电站有序充电方法对充电设施配电容量规划的影响，定义充电负荷同时率为

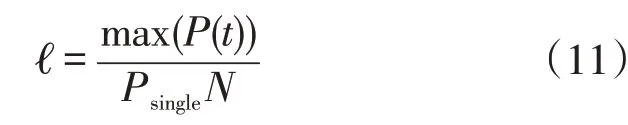
式中：P(t)为t时刻EV的充电总负荷；Psingle为单台EV充电功率；N为EV数量。

则住宅小区充电站EV充电负荷规划计算模型为［8］

式中：S为充电站EV充电负荷规划容量；η为充电效率。

表2为不同EV渗透率下的S对比。通过有序充电的指导，可降低充电站的配电容量规划值，且渗透率越高，效果越明显，对于充电站的配变容量配置具有一定的指导意义。

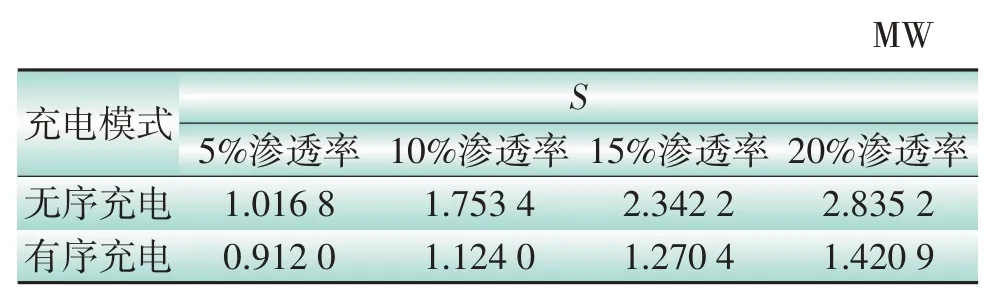
表2 不同EV渗透率下的S对比Table 2 Comparison of S at different EV penetration rates

5.2.3 算法对比

利用充电站负荷的预测误差σ作为本文方法的一个评价指标，并与其他方法进行对比，即

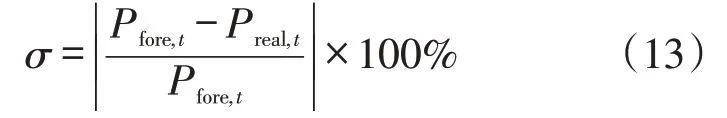
式中：Pfore,t、Preal,t分别为t时刻的预测负荷和真实负荷。

分别设置3种方案进行优化仿真，①利用本文方法模拟EV行为，用遗传算法［9］进行求解；②利用文献［10］的方法，即用蒙特卡洛算法模拟EV行为，用MPGA算法进行求解；③利用本文方法模拟EV行为，用MPGA算法进行求解。结果如表3所示。

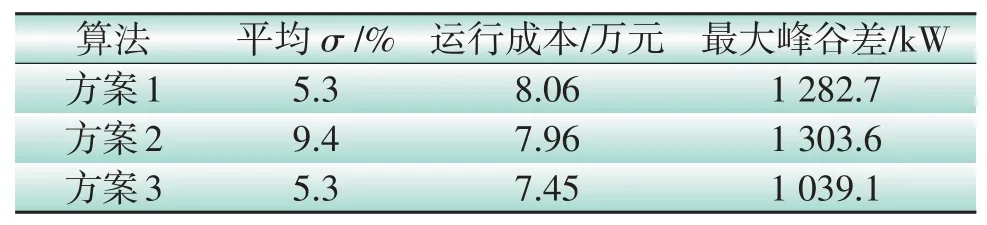
表3 不同算法优化结果对比Table 3 Optimization results comparison of different algorithm

可以看出，采用遗传算法求解，亦能寻到合适的解，降低运行成本和峰谷差，但容易陷入局部最优解；利用蒙特卡洛法模拟EV的行为，大部分时刻的σ值都维持在较高水平；而利用模糊C均值聚类对EV负荷的特性进行提取和分类，并基于马尔科夫链描述EV负荷的随机变化过程，能使模型更接近实际场景，并采用MPGA进行求解，能最大程度地降低运行成本与峰谷差。