电机中ABC到dq0坐标变换的梳理与辨析

付兴贺，陈 锐

（东南大学 电气工程学院，南京210096）

0 引 言

近百年来，坐标变换方法已广泛应用于电气工程的各个领域，解决三相（甚至多相）交流系统中数学模型表征、多变量解耦及不对称分量分析等难题［1⁃2］。随着智能电网的提出，高品质电机系统的迫切需求，以及高效电能变换的发展，交流电气系统的结构日渐复杂，坐标变换方法已成为系统设计、建模和分析的重要手段，因此深入理解和正确使用坐标变换方法非常必要。

Clarke变换和Park变换是两种典型的坐标变换方法，主要用于电机系统建模分析及驱动控制［3⁃4］、电力系统微电网分析［5⁃6］和电力电子逆变器建模［7⁃8］等方面。从数学角度出发，Clarke变换和Park变换实现了机电或电气系统中物理量在不同坐标系下的表征。目前，广大工程技术人员及专家学者已基本了解Clarke变换和Park变换，能够尝试应用Clarke变换和Park变换，分析交流系统的动态性能。但是，也出现了没能抓住坐标变换的本质问题、对坐标变换方法使用不当的情况，导致教学和科研工作偏离主题、得出错误结果。文献［9］对坐标系的定义有误，并且采用坐标变换的假设条件表述不清；文献［10⁃17］将Park变换定义为从两相静止到两相旋转的坐标变换，理解有失偏颇；文献［16］混淆了等功率和等幅值变换矩阵；文献［10，15，17］未给出d，q坐标轴的定义，并且混淆了d，q轴的基本概念。文献［18］虽然点明了坐标变换误用的问题，但此类现象仍然没有得到足够重视。因此，回溯Clarke变换和Park变换的发展历程，深究Clarke变换和Park变换的本质内涵，对于教学和科研工作具有重要意义和价值。

部分学者试图从数学角度出发，重新审视Clarke变化和Park变换的推导过程，明确两种变换的数学意义。文献［18］在综合矢量基础上利用三角函数关系对ABC／αβ0变换进行了数学意义的推导，说明了限制条件；文献［19⁃20］在基于空间旋转坐标的基础上开展了几何分析工作，分析过程相对复杂；在三相交流系统的基础上，文献［21］提出了四相到任意相交流系统Park变换矩阵推演方式；文献［22］利用求电感矩阵特征值的方法，解得ABC／dq0变换矩阵，该方法具有一定的普适性。总体而言，上述工作更多的意义在于数学或几何证明，缺乏物理指导意义，同时也没有指出坐标变换间的相互关系，没有指明应用过程的注意事项。在上述工作基础上，本文旨在继续加深和完善对Clarke和Park变换的认识，指出两种变换应用中出现的问题及应对措施。

首先，本文给出了Clarke变换和Park变换的初始定义，揭示了两种变换的初衷和目的。然后，理论推演了电机分析中常用的三相静止坐标系、两相静止坐标系及两相旋转坐标系之间的变换，分析了几种变换矩阵之间的联系与差异。接着，指出了应用中存在的混淆坐标定义、误解坐标变换及使用不当等问题。最后，以永磁同步电机调速系统为例，开展分析和示教工作，验证不同的变换矩阵及其误用对系统性能的影响。

虽然本文不属于技术或方法创新，但通过对坐标变换开展深入细致的梳理与辨析，有助于工程技术人员熟悉坐标变换的发展历程，理解理论基础，掌握使用方法。此外，对高等学校教师及学生而言，本文关于坐标变换的历史探究、相关定义澄清及误用纠正等方面的尝试，也将为课堂教学、理论学习和实践指导等提供借鉴和帮助。

1 Clarke变换与Park变换的初始定义

1.1 Clarke变换

1918年，Fortescue提出了用于分析不对称三相系统的对称分量法，即将不对称的三相分量分解为正序、负序和零序分量。三相的正序、负序分量相序相反，零序分量幅值、相位均相同。1937年左右，Clarke提出了αβ0分量法以改进对称分量法，简化了电力系统中不对称问题的分析。1951年，Clarke指出采用αβ0坐标系可以简化电机中部分公式的推导过程［1］。因此，她将原来用于电力系统分析的αβ0分量法推广到同步电机分析中，建立了瞬时相量ABC和αβ0分量、αβ0分量和dq0分量之间的变换关系。随着坐标变换在电机领域中的广泛应用，考虑到Clarke的理论贡献，ABC／αβ0变换逐渐被称为了Clarke变换。

1.2 Park变换

1899年，Blondel针对凸极同步电机的结构特点提出了双反应理论，用两个相对简单的交、直轴电枢反应描述复杂难解的电枢反应。即将电枢基波磁动势Fa分解为作用在直轴上的直轴电枢反应磁动势Fd和作用在交轴上的交轴电枢反应磁动势Fq［23］。1929年，Park在双反应理论的基础上提出了分析同步电机的一般化方法：将磁链、电流、电压等三相物理量等效成随转子同步旋转的直轴分量与交轴分量，消除了变量之间的耦合。根据同步电机方程及ABC与dq0坐标系之间的对应关系，Park推导出由空间静止的ABC坐标系变换到空间旋转的dq0标系的变换式，即Park变换。在分析中，一般均假设三相对称，故0轴略去。因此，Park变换本质上是ABC／dq0的坐标变换方式。

2 电机分析中的坐标变换

2.1 坐标变换的目的

在直流电机中，励磁绕组轴线方向为主磁通方向，该方向定义为直轴（d轴），电枢绕组产生的电枢磁动势的轴线方向则被定义为交轴（q轴）。电枢绕组通过位于几何中性线上的电刷与电源连接，因此，电枢磁动势的轴线被电刷限定在q轴。d轴与q轴相差90°电角度，d轴磁场与q轴磁场正交，这是直流电机数学模型及其控制系统比较简单的根本原因。

交流电机是一个多变量、非线性、强耦合的系统，各物理量（电压u、电流i、磁通Φ、电磁转矩Te等）相互关联，存在较强的耦合。例如，电磁转矩正比于主磁通Φ和电流i，而Φ和i是随时间变化的函数。因此，电磁转矩的表达式中将出现两个变量的乘积项，电机的数学模型复杂。采用坐标变换的目的就是将交流电机的物理模型等效为直流电机。

在理想条件下，当空间上三相互差120°的交流电机定子绕组中通以相位互差120°、频率为ω的三相正弦交流电时，在空间上产生一个角速度为ω的旋转磁场。同理，在空间上相互垂直的两相绕组（α，β）中通入相位互差90°、频率为ω的两相平衡交流电流，也能建立同样的角速度为ω的旋转磁场。在两个相互垂直的静止绕组d和q中分别通入直流电流产生的合成磁动势也是静止的。如果让两个绕组以一定速度旋转，则原来静止的合成磁动势变为旋转磁动势。通过控制直流电流大小和旋转速度，可保证该旋转磁动势与交流电流形成的旋转磁动势等效，即该套直流绕组与前述的交流绕组等效。从静止侧看，d和q绕组是与三相或两相交流绕组等效的旋转直流绕组；从旋转侧（d和q绕组）看，它们是相互垂直的静止直流绕组［24］。

为了表达不同绕组之间的关系，坐标变换方法应运而生，即利用不同的坐标系用数学语言表达绕组间的等效关系。从数学角度出发，上述过程分作两步执行更好理解：将三相静止交流绕组等效为两相静止交流绕组，再等效为两相旋转直流绕组，即从ABC坐标系变换到αβ0坐标系再变换到dq0坐标系。经过上述坐标变换，交流电机具有了直流电机的特点，交流电机的数学模型大为简化。

2.2 三相静止到两相静止坐标变换

在电机分析中，常用的Clarke变换与最初的αβ0分量法在物理意义上不尽相同，但在数学意义上相似。在两相静止坐标系中，坐标轴可以定义为x，y或者m，n。但是，该变换由Clarke提出，并由αβ0分量法推广而来，故坐标轴的定义保持不变，仍采用α，β变量描述。三相静止坐标系和两相静止坐标系间的关系如图1所示。

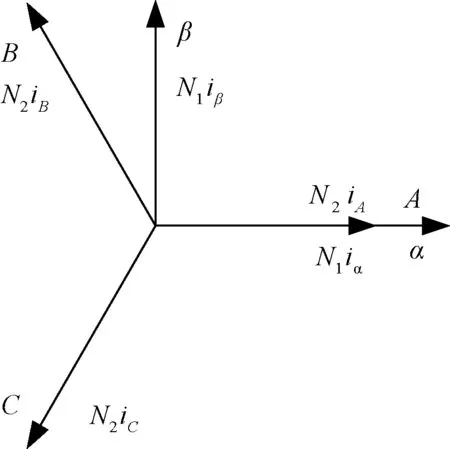
图1 ABC／αβ0坐标变换示意图

根据变换前后物理量之间的关系，Clarke变换包括等幅值变换和等功率变换。

2.2.1 等幅值变换

电机矢量控制中常用的是等幅值变换。根据变换前后旋转磁场等效的原则，等幅值变换需维持综合矢量（电流、电压等）的幅值不变。

假设复平面上任意矢量x可以用ABC坐标系（α轴为复平面实轴，且与xa方向重合；β轴为复平面虚轴）下互差120°的分量xa，xb，xc表示。定义：

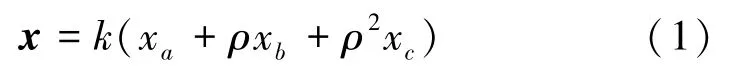
根据式（1）将x写成复平面表达式，即：

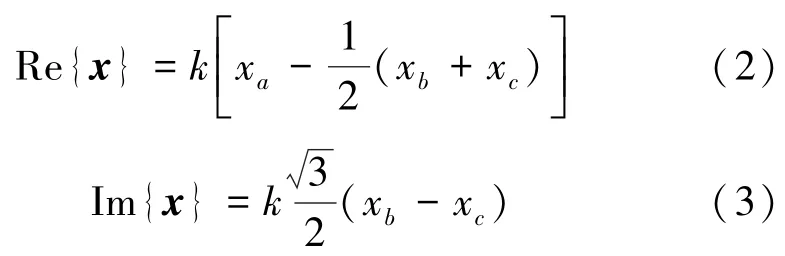
为分析方便，引入变量x0，定义：

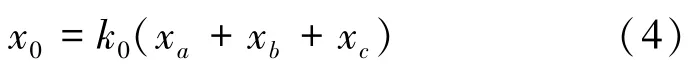
由式（4）可得：

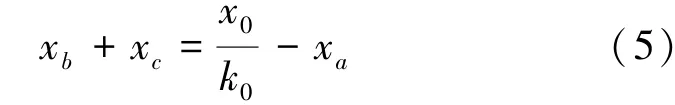
将式（5）代入到式（2）中可得：

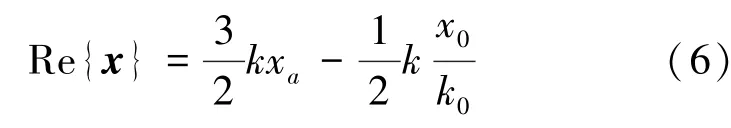
等幅值变换时，规定：

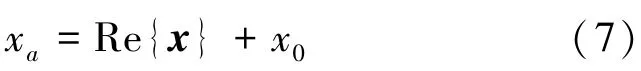
将式（7）代入到式（6）可得：

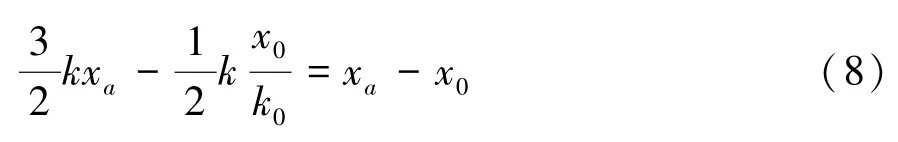
根据待定系数法，由式（8）可解得：

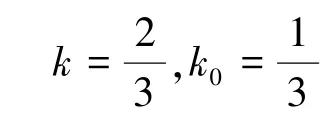
将解得的k，k0值代入式（2）、式（3）可得等幅值的变换形式：

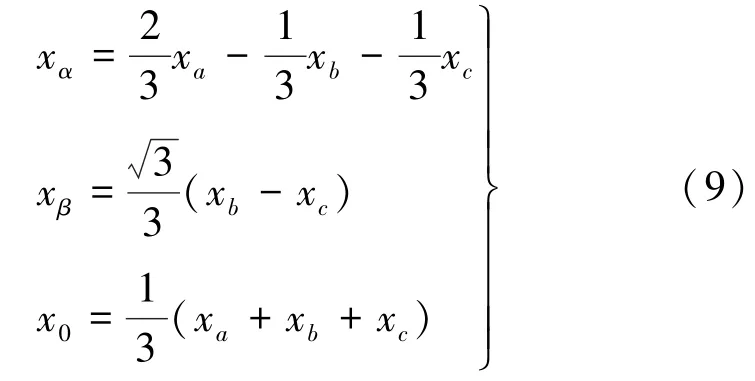
将式（9）写为矩阵形式：

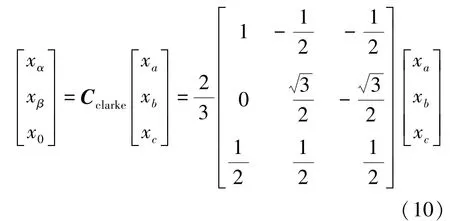
式中：Cclarke为等幅值的Clarke变换矩阵。

2.2.2 等功率变换

区别于等幅值变换，在使用等功率变换矩阵时需注意保持变换前后系统的功率不变［25］。

如图1所示，结合上述原则，有：

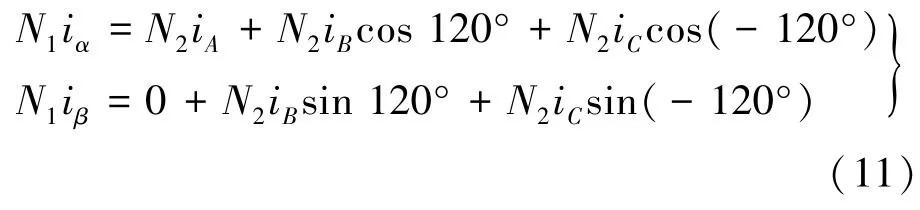
式中：iα和iβ表示αβ坐标系下的两相电流；iA，iB和iC表示ABC坐标系下的三相电流；N1和N2分别表示两相和三相绕组的有效匝数。

式（11）经整理后，用矩阵表示：

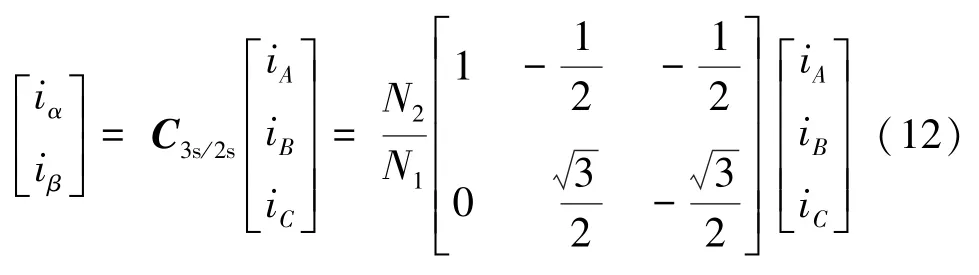
变换矩阵C3s／2s不是方阵，不能求逆，需引入一个独立于iα，iβ的新变量i0，称为零轴。零轴同时正交于α轴和β轴，构成三维空间的αβ0坐标系。

定义：

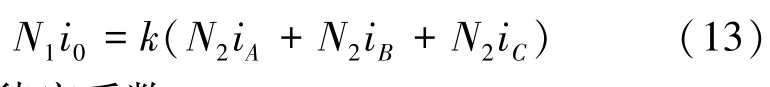
式中：k为待定系数。

引入新的变量后，式（12）可改写：

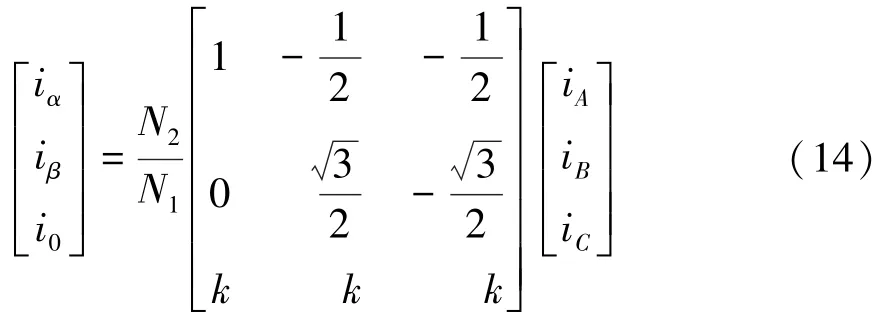
将两相静止坐标系下的电压u和电流i变换到三相静止坐标系下的电压u′和电流i′，因此有：

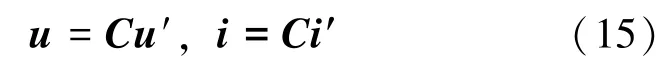
为实现可逆变换，C－1为矩阵C的逆矩阵，所以：

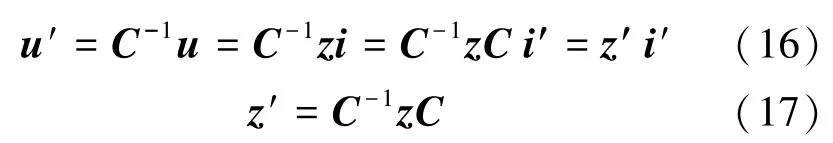
式中：z，z′为不同坐标系下的阻抗矩阵；u，u′，i，i′为不同坐标系下电压和电流的行向量和列向量。

为满足功率不变原则，在一个坐标系下的电功率应等于另一坐标系下的电功率，即：

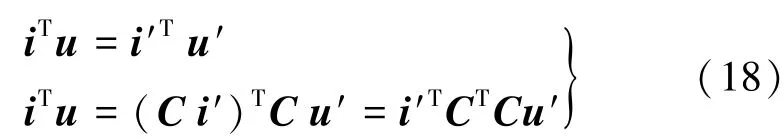
式中：CT为C的转置矩阵；iT为i的转置矩阵；i′T为i′的转置矩阵。

为使式（18）成立，必须有

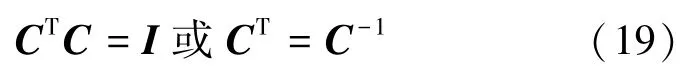
式中：I为单位矩阵。

因此，根据式（19），在功率不变原则的基础上，变换矩阵C应该是一个正交矩阵。

定义矩阵C及其转置矩阵CT：

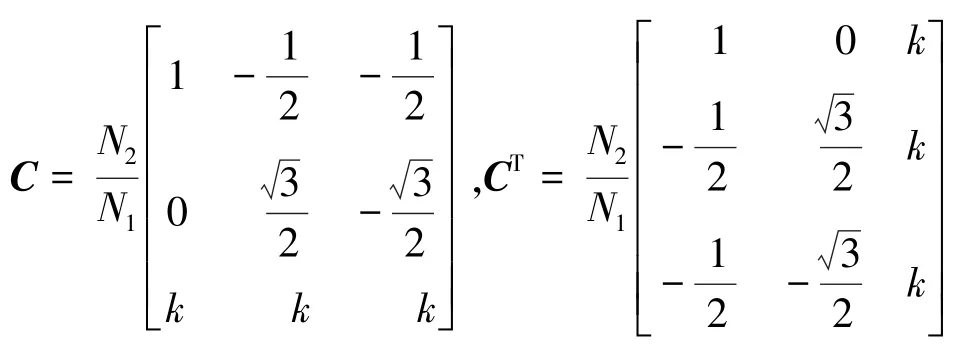
将C及CT代入式（19），则有：

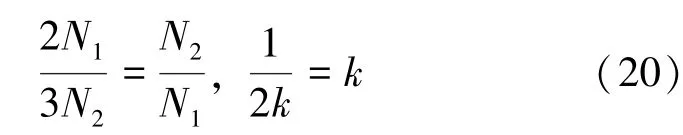
根据式（20），可分别求得：

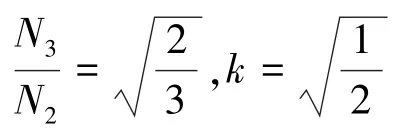
根据解得的值可求得C和C－1：

“我国的天主教、基督教一方面是宗教问题，另一方面，在长时期中又被帝国主义利用为对我国进行文化侵略的工具，其中一部分组织又被帝国主义利用为进行间谍活动的机关。这两个宗教在我国都办有教堂、学校、医院及其他文化事业及救济事业机关，都受外国津贴，都有大量外国传教士占据领导地位。”⑧针对这一情况，河南展开了一系列全面清理帝国主义在宗教领域的影响的工作。

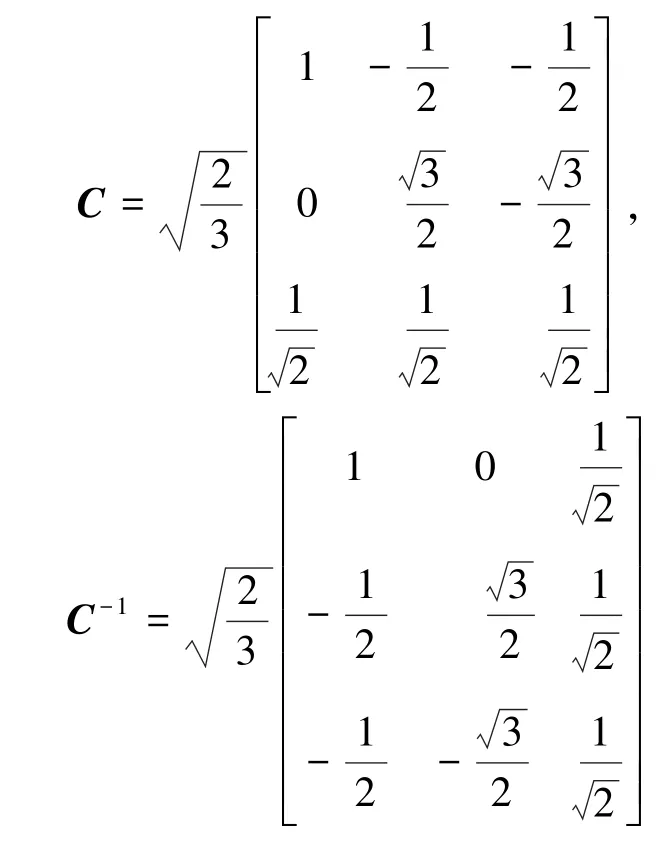
因此，等功率的变换式：

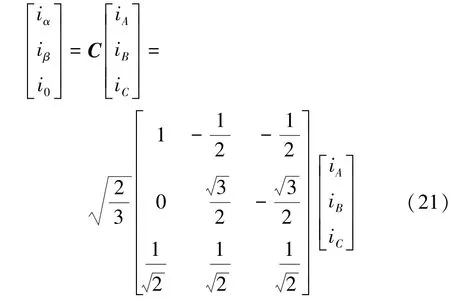
等功率的逆变换式：

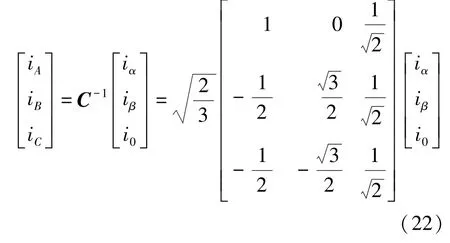
上述三相静止坐标系到两相静止坐标系的变换与Clarke当初为了进行不对称分析而采用的αβ0分量法的性质不同，目的不同。但是，Clarke变换与αβ0分量法具有相似性，都实现了三相物理量到两相物理量的转换，因此人们将上述过程称之为Clarke变换。笔者认为电机分析中的Clarke变换是一种广义的变换，与最原始的αβ0分量法在本意上存在一定区别。

2.3 两相静止到两相旋转坐标变换

在Clarke变换所定义的αβ0坐标系中，一般规定α轴超前β轴90°，且α轴与A相绕组轴线方向重合。但对于Park变换，不同文献给出了不同的dq0坐标系的定义。目前，主要有三种不同的dq0轴定义方式，具体如图2所示。图2（a）中，d轴超前q轴90°，规定d轴与A轴间的夹角为α；图2（b）中，q轴超前d轴90°，规定d轴超前于A轴的夹角为α；图2（c）中，q轴超前d轴90°，规定d轴滞后于A轴的夹角为θ。

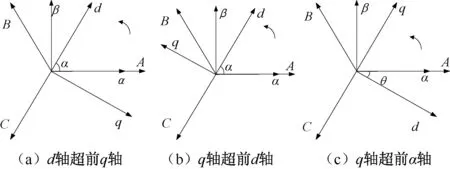
图2 不同dq0轴定义的坐标系统示意图

不同的坐标轴定义，从ABC到dq0坐标系的变换矩阵不同，即对应上述三种情况的变换矩阵不同。下面对图2（a）进行详细分析。为便于理解，由静止的αβ0坐标系变到dq0旋转坐标系的变换称为2s／2r变换。

由图2（a）可得：

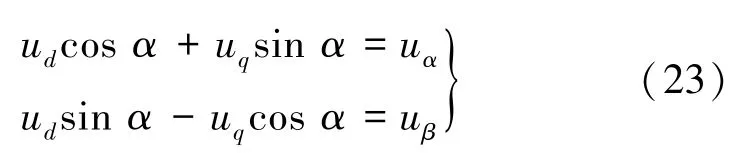
将式（23）改写为矩阵形式：

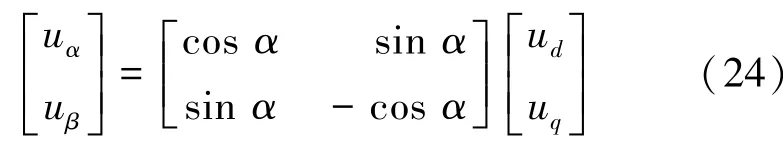
对式（23）进行变换可得：

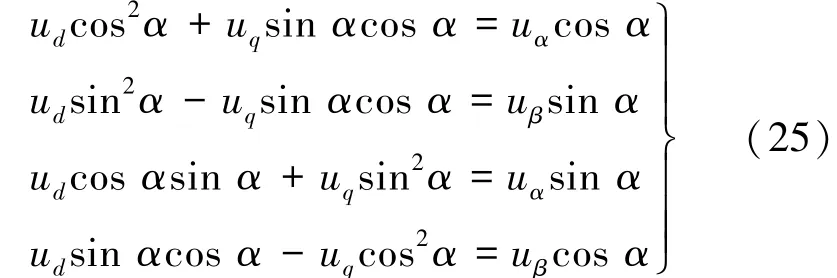
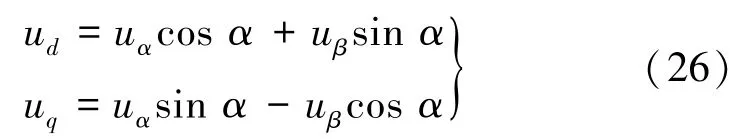
将式（26）改写为矩阵形式：

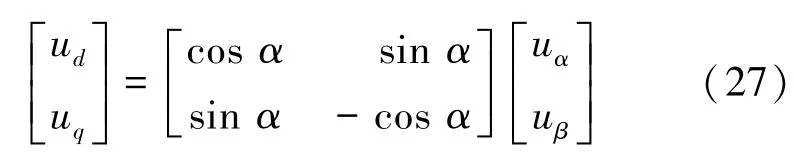
将式（27）与Clarke等幅值变换矩阵相乘，可得ABC／dq0变换的等幅值变换矩阵T3s／2r：

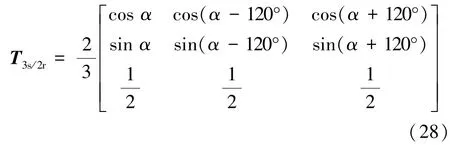
将式（27）与Clarke等功率变换矩阵相乘，可得ABC／dq0变换的等功率变换矩阵T3s／2r：

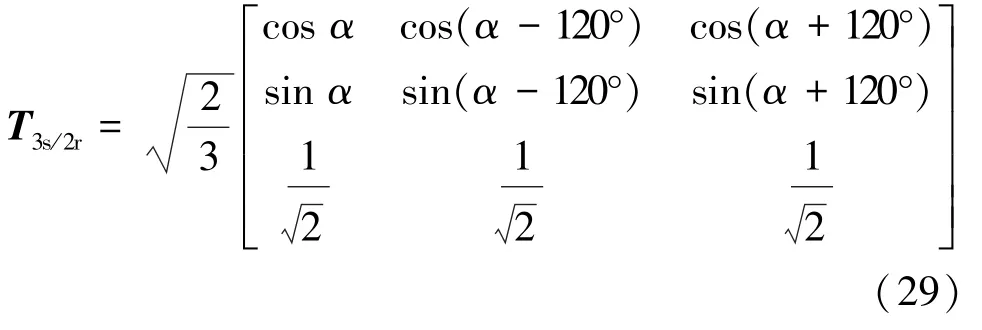
式（28）和式（29）分别为等幅值和等功率的ABC／dq0变换矩阵。

与图2（a）相比，图2（b）和图2（c）中对dq轴的定义不同，所对应的2s／2r变换矩阵也不同，因此最终的ABC／dq0变换矩阵有所差别。

对于图2（b），对应的2s／2r变换矩阵：

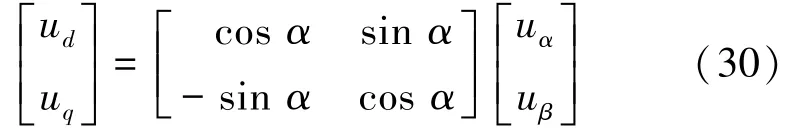
将式（30）与Clarke等幅值变换矩阵相乘，可得ABC／dq0变换的等幅值变换矩阵T3s／2r：

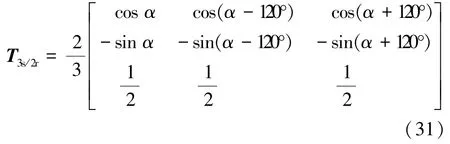
对于图2（c），对应的2s／2r变换矩阵：

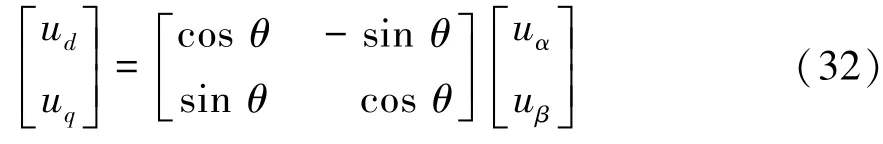
将式（32）与Clarke等幅值变换矩阵相乘，可得ABC／dq0变换的等幅值变换矩阵T3s／2r：

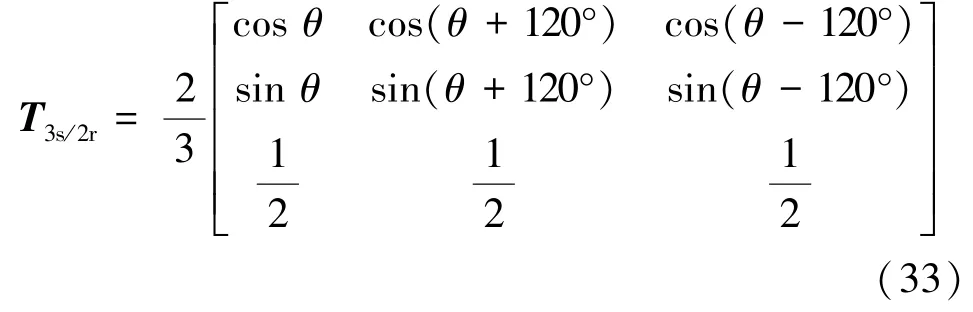
在等功率变换时，图2（b）和图2（c）的情况读者可以自行推导，本文不再赘述。

上述两相静止坐标系到两相旋转坐标系的变换与当初Park为了分析凸极电机电枢反应而采用的dq0坐标变换的最终目的相同。但是，原始的Park变换是指从ABC到dq0的坐标变换，而目前大部分文献所指的Park变换专指从αβ0到dq0的坐标变换。由此，笔者认为目前的Park变换是一种“狭义”的Park变换，仅是原始Park变换的一部分。

3 坐标变换的误用及混淆

3.1 误用实例

由于文献编辑工作失误、排版印刷错误、参考引用过程漏洞等原因，部分文献、资料及书籍在介绍、使用Clarke变换和Park变换时出现偏差，致使三相对称交流量到两相直流量的变换失败，最终误导工程技术人员、延缓工程项目开发以及延误科研项目攻关。

文献［26］中（1.2.1 Clarke变换与仿真）提到：

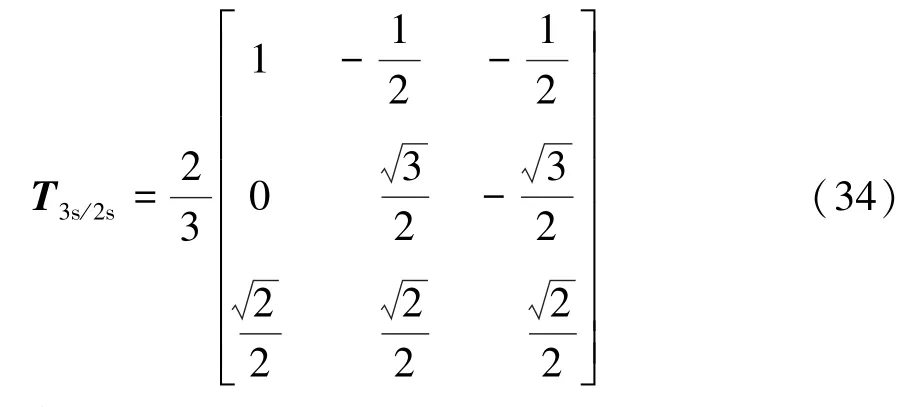
与式（10）和式（21）相比，式（34）表示的Clarke变换矩阵既不是等幅值变换，也不是等功率变换。

该书中后文（1.2.2 Park变换与仿真建模）提到：

根据式（35），我们推断式（34）应是等幅值的Clarke变换。因此，根据本文前面给出的定义，式（34）最后一行系数应为另外，文献［16］也存在该问题。

当建立被控对象在dq0坐标系下的数学模型时，文献［9］在进行坐标变换时没有给出相应的假设（前提）条件，对αβ坐标轴的定义有误，并且混淆了等功率和等幅值的变换，推导过程不连贯。文献［10］未给出dq坐标轴的定义。文献［13］将id作为iq进行控制，混淆了dq轴的基本概念。文献［17］描述的dq坐标系与dq轴的实际定义不相符。上述情况出现较多，本文不再赘述。

3.2 定义混淆

目前，不同文献对Park变换的定义存在一定分歧。诸多电机及其控制的相关文献、书籍等将Clarke变换定义为ABC／αβ0变换，将Park变换定义为αβ0／dq0变换［8⁃16，26］。但是，文献［27］中将Park变换定义为ABC／dq0变换，具体变换矩阵：

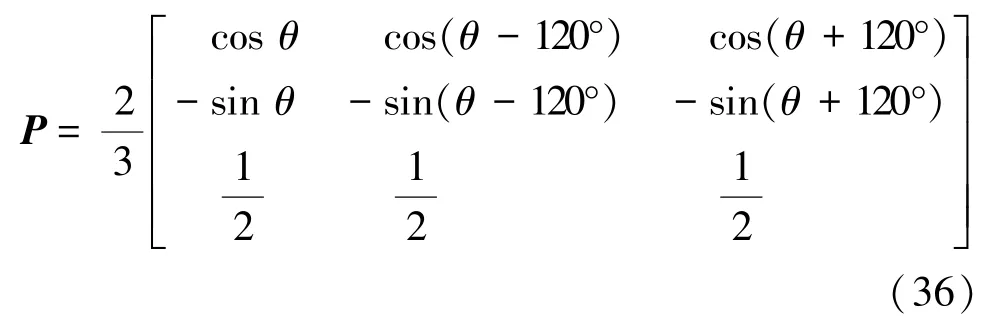
同样的，文献［17］也提到：“交流电机理论所研究的内容主要是处于相对运动状态的电路行为问题，由于电机中布置有许多在磁路上耦合又处于相对运动中的电路，分析工作显得十分复杂，甚至难以进行。1929年，Park针对凸极同步电机转子不对称的特点，提出了著名的Park方程。这是一个将实际存在的三相静止电路中的电压、电流等变量变换到与之等效的旋转dq轴参考坐标系内相应量的坐标变换公式。”

回顾Park于1929年发表的文章，该文章在双反应理论基础上推导出ABC／dq0变换，并未经过αβ0坐标系统的转换，式（37）是最初Park提出的变换方程。

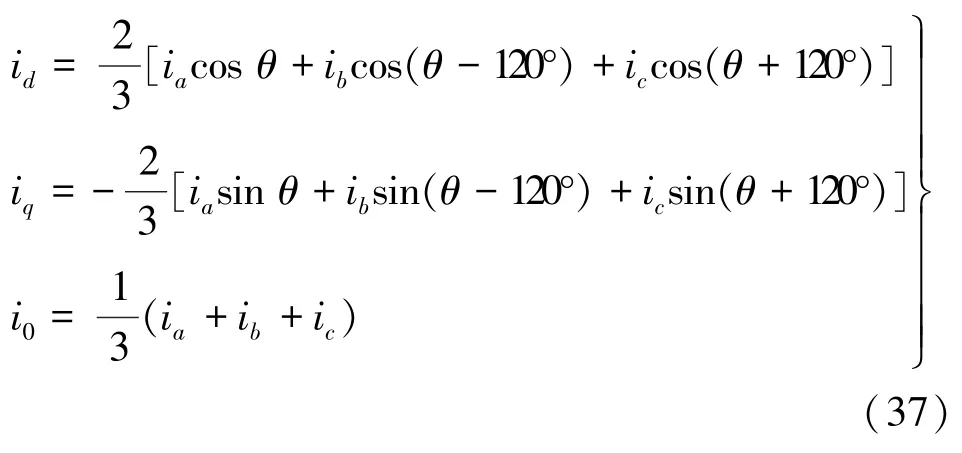
值得注意的是，Clarke首次提出αβ0坐标系大约是在20世纪30年代末期，因此，无论是从时间上来看，还是从推导原理与过程上来看，Park变换所指的应当是ABC／dq0变换，与αβ0并没有直接关系。若将αβ0坐标系作为Park变换（3s／2r）的中间环节，即我们所熟知的3s／2s／2 r变换，可使抽象的坐标变换更容易理解，在一定程度上简化推导过程。虽然这种经αβ0坐标系过渡的坐标变换推导方法已在教学和科研中广泛采用，但原则上Park变换本质是由ABC三相静止坐标系变换到dq0旋转坐标系这一点不可混淆，且有必要澄清。在教学与科研过程中，部分文献忽略了Park变换与Clarke变换的历史演变过程，混淆了两种坐标变换间的先后关系，导致目前Park变换定义混乱。

虽然，目前所应用的Clarke变换和Park变换与它们的原始定义存在偏差，但为了避免引起混乱，便于阅读和理解，本文在后续讨论中暂且采用Clarke变换和Park变换分别描述ABC／αβ0变换和αβ0／dq0变换。

4 仿真分析及验证

4.1 基本坐标变换的仿真分析

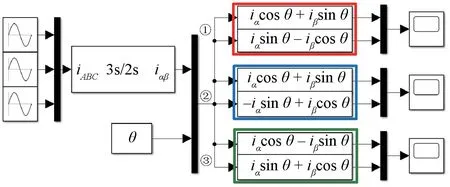
图3 坐标变换仿真模型

图3为在Simulink软件中搭建的等幅值Clarke变换和不同dq0坐标系下的Park变换仿真模型，用于对比坐标变换的不同结果。

仿真模型的输入信号为三相对称的幅值均为1的正弦电流信号，频率为50 Hz。图3中，3s／2s模块即为等幅值的Clarke变换，①、②、③三个模块分别对应图2（a）、图2（b）、图2（c）中三种不同dq0坐标系下的2s／2r变换。

Clarke变换的结果如图4所示。α轴分量超前于β轴90°，且变换前后变量的幅值相等，均为1。

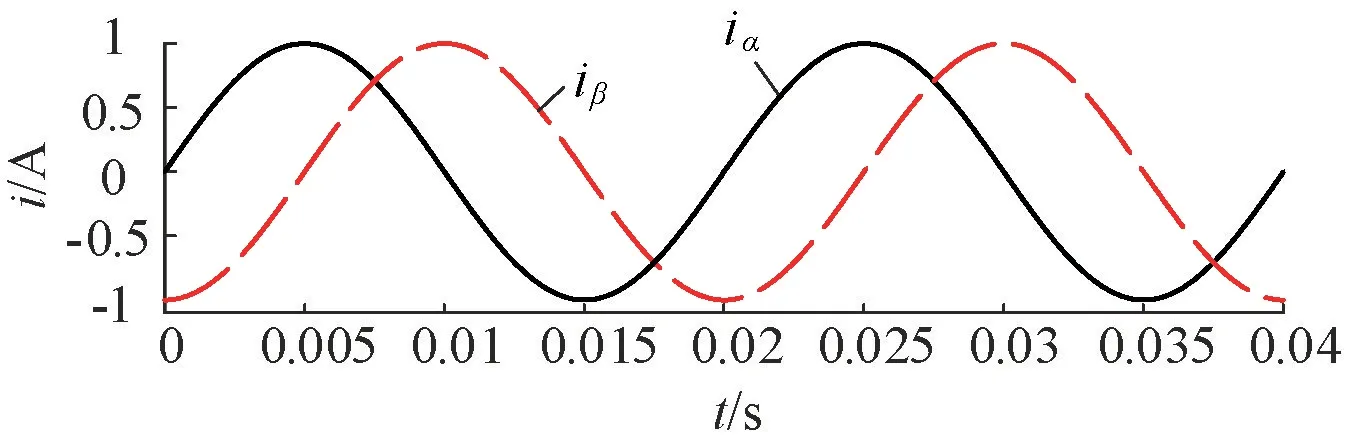
图4 Clarke变换仿真结果

图2（a），图2（b）和图2（c）三种坐标系下Park变换的结果分别如图5（a），图5（b）和图5（c）所示。

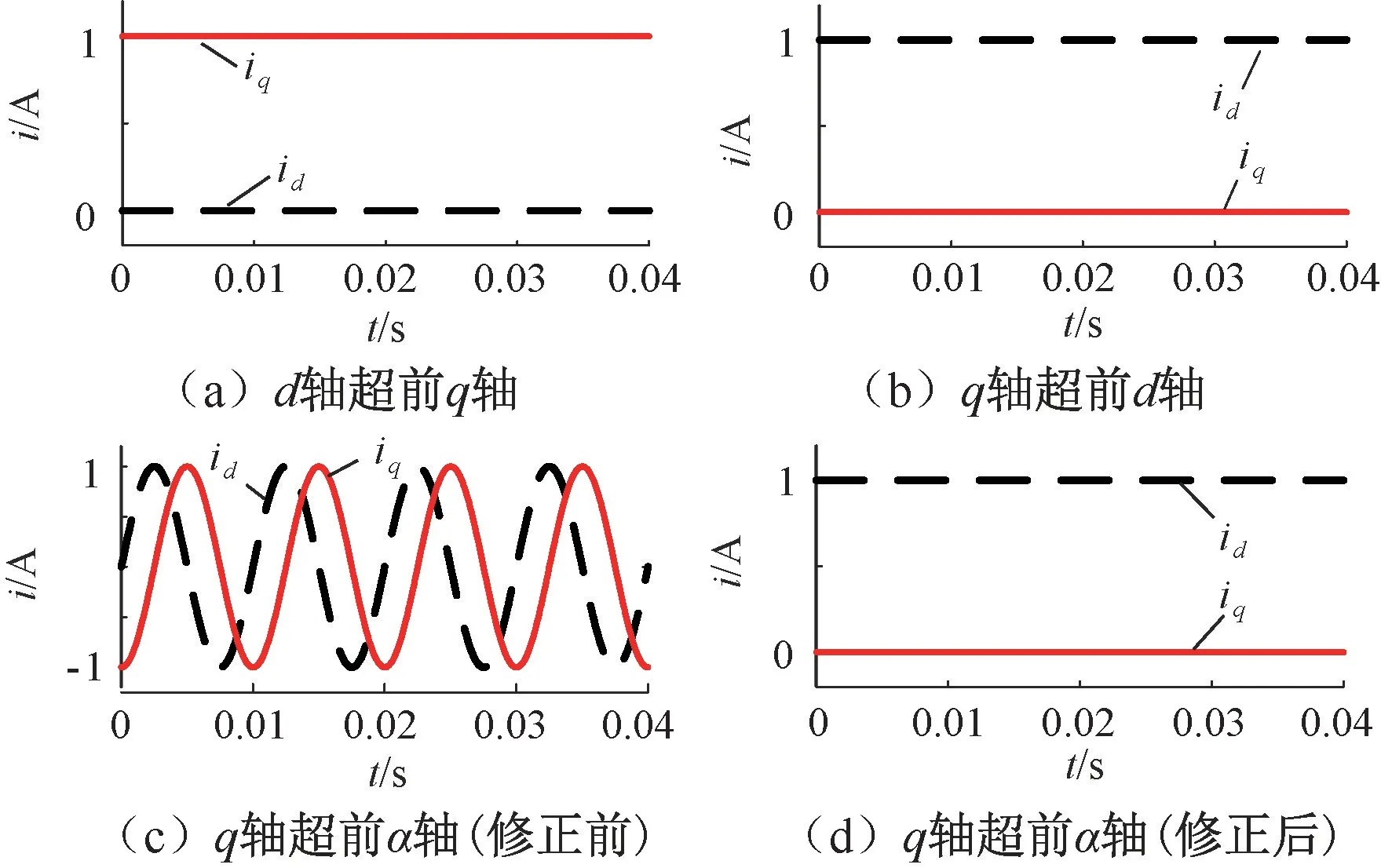
图5 Park变换仿真结果

由于坐标轴定义不同，在图5（a）和图5（b）中变换后的dq轴分量颠倒，或体现为dq轴超前和滞后的变化。在图5（c）中，Park变换未能将三相对称的正弦量变换为两相直流量，分析图2（c）的dq0坐标系，其定义的角度θ为d轴滞后于α轴的角度，相较于图2（b）所定义的角度α，两者之间关系满足θ＝－α。由于仿真模型中采用的角度为α，因此修改仿真模型，将α乘以－1以符合对θ的定义，结果如图5（d）所示。

上述仿真分析揭示了不同dq0坐标系定义对应的坐标变换结果差别，给出了输出错误的具体形式。相关科研人员可以借鉴该结果，指导各自的仿真分析工作。

4.2 错误使用变换矩阵的影响

MATLAB／Simulink软件库中含有封装好的坐标变换模块，该模块默认的坐标系定义与图2（b）一致。建立电机数学模型时，若采用图2（b）的dq0坐标系，则仿真时可直接调用坐标变换模块。但是，若所建立的数学模型与仿真模型采用的坐标系不一致，则无法得到预期的结果。例如，若建立电机数学模型时选用图2（c）的dq0坐标系，而仿真时直接调用Simulink库中的坐标变换模块，会导致错误出现。此时所得dq轴分量不是直流量，无法达到预期效果，系统不稳定。

以永磁同步电动机调速控制系统为例，采用id＝0的控制策略开展仿真分析。将三相电流变换为旋转的两相直流量，分别对id和iq进行控制。

1）采用图2（b）的q轴超前d轴（常用）坐标系，即Simulink中坐标变换模块默认的定义，仿真结果如图6所示。永磁同步电动机能够正常运行，在准确跟踪给定转速的同时，若负载突变，转速仍可以维持稳定且波动较小，控制性能较好。

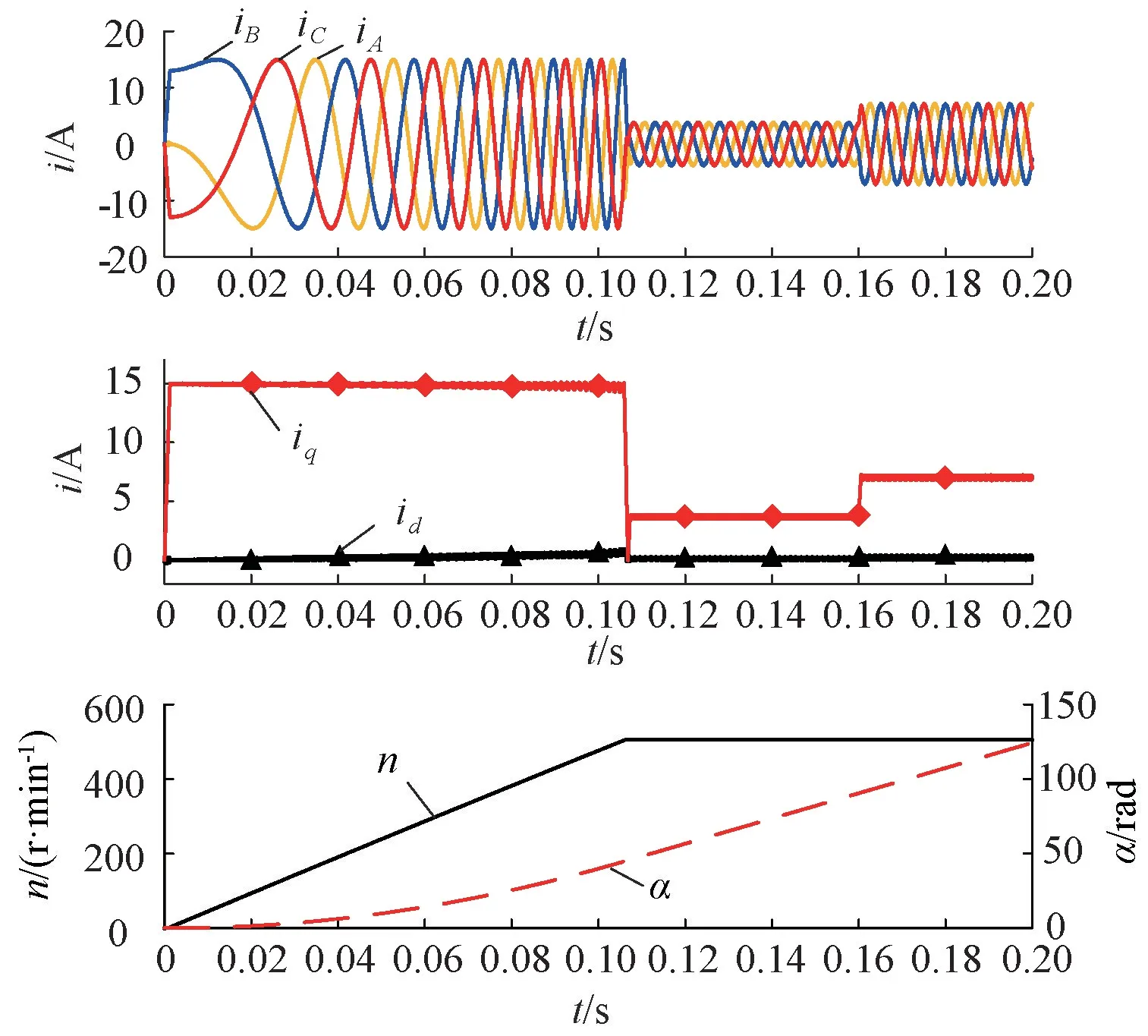
图6 Park变换中q轴超前d轴时的仿真结果

2）采用图2（a）中的d轴超前q轴的坐标系，仿真结果如图7所示。假设建立的数学模型与仿真模型采用的坐标系不一致，即Park变换矩阵不同，此时若不对仿真模型加以调试、改动，整个系统不能按照预期的控制效果正常运行。经分析，该坐标系与前述q轴超前d轴坐标系的区别在于两者q轴的方向相反（相差180°）。因此，在模型中将q轴电流乘以－1再进行控制，电机可以稳定运行且控制性能较好。具体仿真结果如图7所示，与图6所示类似，此处不再赘述。

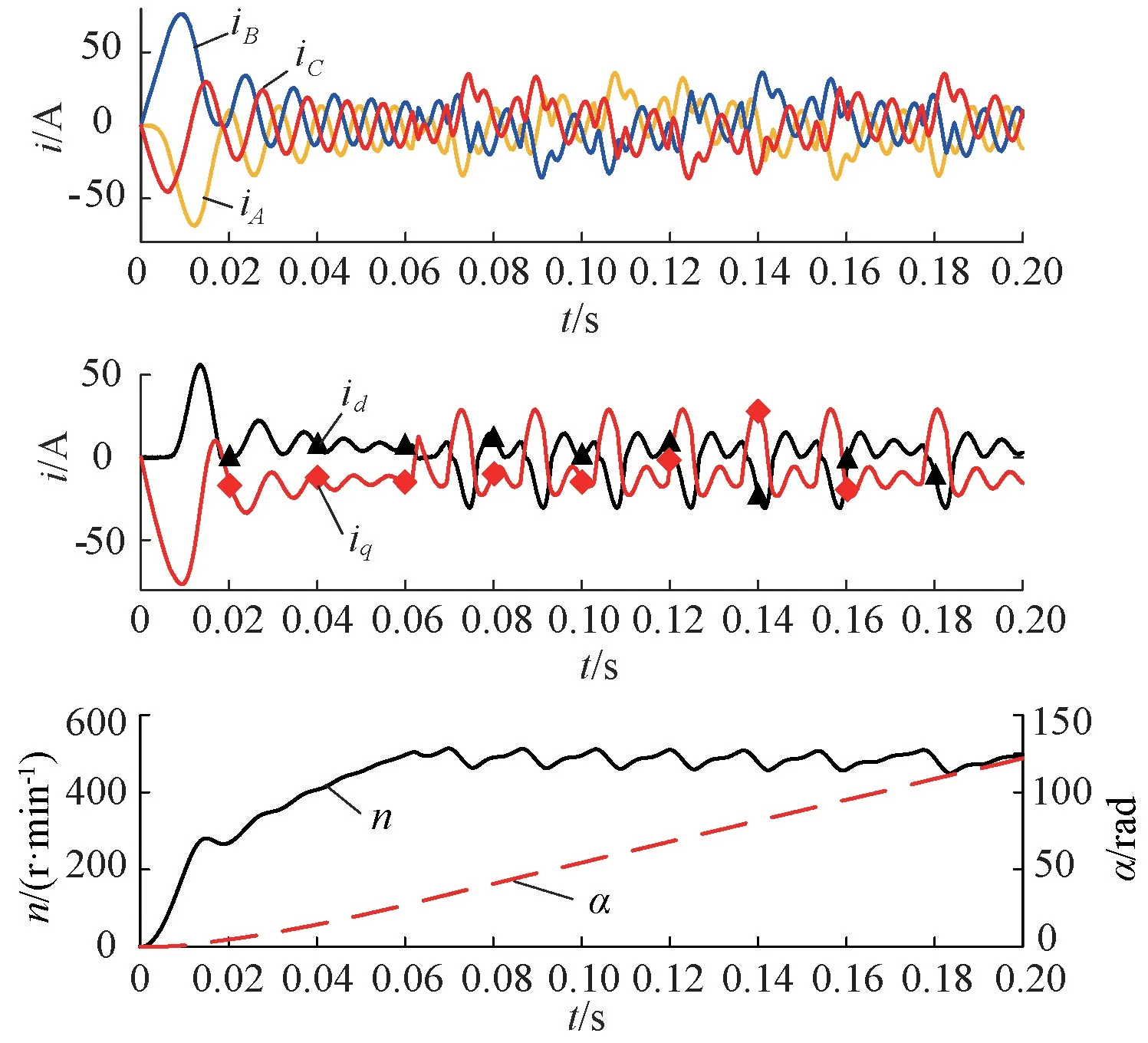
图7 Park变换中d轴超前q轴时的仿真结果

3）采用图2（c）中的q轴超前d轴的坐标系，对角度的定义与图2（b）不同，仿真结果如图8所示。

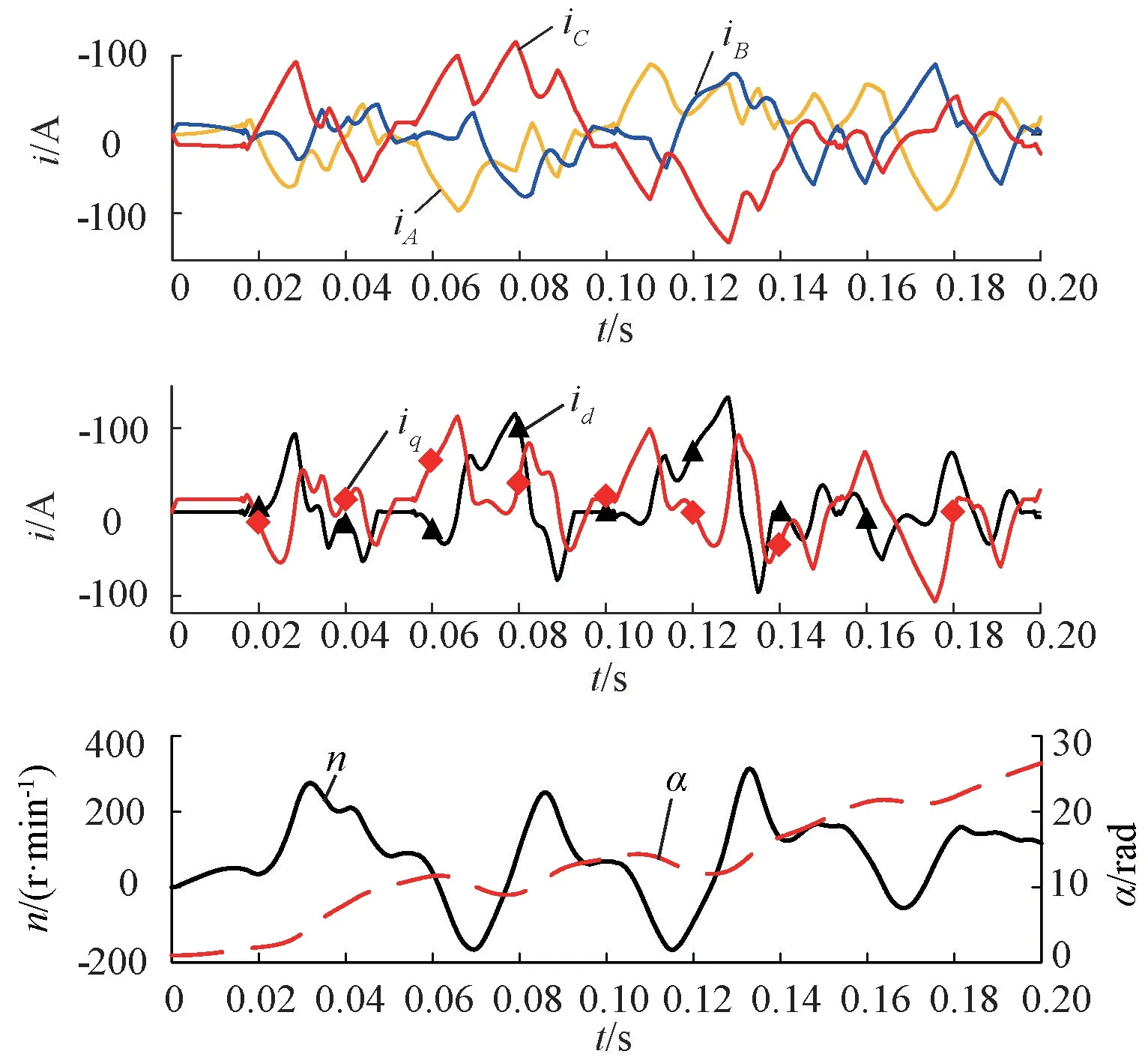
图8 Park变换中q轴超前α轴时的仿真结果

若不对模型进行调试，此时系统不稳定，无法按照预期正常运行。根据前述分析，该坐标系定义的角度θ为d轴与α轴之间的夹角，与仿真模型实际采用的角度α之间满足θ＝－α。因此，修改模型中对应的电角度，将其乘以－1再进行变换，电机正常运行。

对比上述三种情况可以发现，当dq轴的选取与模型中坐标变换矩阵不一致时，整个控制系统出现紊乱，无法达到预期的调速效果，甚至系统无法正常运行。

4.3 总结与分析

根据理论与仿真分析结果，使用Clarke变换与Park变换时需注意：

1）采用坐标变换时，需假设三相绕组空间相差120°，且绕组内的各物理量幅值相等，相位互差120°，若实际不满足上述假设条件，变换后的参数无法解耦；

2）选定等幅值或等功率变换后，应保证数学建模和仿真分析采用的变换矩阵一致，不可随意更改；

3）区分αβ轴和dq轴的超前滞后关系，不应混淆：αβ0坐标系为静止坐标系，对αβ分量的超前滞后判断应参考各自的时间相位；dq0坐标系为旋转坐标系，对dq分量的超前滞后判断应参考各自的空间位置；

4）旋转角α（或θ）定义为d轴与α轴的夹角，仿真分析与数学建模所采用的角度应保持一致。

目前Park变换中初始定义的q轴超前d轴的坐标系已被广泛使用，并且Simulink中默认的坐标变换模块也采用了该定义，仿真时直接调用该模块或简单调试后基本可以保证系统正常运行。在实际仿真过程中，遇到上述系统不稳定的情况并不常见。但脱离仿真软件，独立建立电机数学模型时，部分学者、学生及工程技术人员并不注意坐标系的定义和采用坐标变换的前提条件等问题，直接套用变换矩阵。实际上，数学建模采用的坐标系与仿真建模采用的坐标系可能不一致，故人为地将数学建模与仿真建模割裂开，这也是目前高度依赖仿真软件而忽视理论分析的体现。此外，若实际上应用坐标变换的条件并不满足而仍采用坐标变换进行分析，那么所得结论也是不可靠的。出现上述情况后，虽然仿真系统经过调试能够正常运行，但对坐标变换定义不清晰、理解不深刻、用法不恰当等问题没有明显体现出来，因此造成无法真正掌握、灵活运用Clarke变换与Park变换等问题。

5 结 语

本文梳理了Clarke变换和Park变换的发展历程，分析了对坐标变换定义混淆和由于阐述不严谨导致的变换矩阵误用等问题，通过永磁同步电动机调速系统仿真展示了变换矩阵的误用后果。通过本文不同角度的分析，希望学生、学者和工程技术人员加深对坐标变换的理解，激发对基本理论的探索，树立严谨求实的态度，合理、准确地应用坐标变换方法。