电梯补偿链动态悬挂特性分析

傅武军

（三菱电机上海机电电梯有限公司 技术开发中心，上海201109）

0 引言

曳引乘客电梯作为高层建筑中垂直运输工具，在现代社会中的应用越来越广泛。乘客电梯是一个复杂的机电系统，由成千上万个零部件组成，这些零部件集中安装在电梯的井道中。运动部件之间的相对位置决定了所需要的安装空间，在对部件运动范围进行确认的基础上，对部件的位置进行合理的安排，否则会出现运动部件干涉的情况。

电梯补偿链一头悬挂在轿厢上，另一头悬挂在对重上，随着电梯上下运行而运动[1]，主要用来平衡电梯曳引钢丝绳的质量（如图1）。研究补偿链的动态悬挂特性有助于厘清电梯运行过程中补偿链和电梯井道中其它部件的位置关系，对于合理设置井道部件有重要指导意义。文献[2]、[3] 采用悬链线的方法对补偿链的悬挂曲线进行了分析，但是该分析方法只适用于静态曲线，没有考虑电梯运行过程中加速度对补偿链的影响，而且在实际运行的曳引乘客电梯中，由于加速度的影响会导致补偿链产生较大幅度的晃动。本文考虑求解带加速度的曳引电梯补偿链运动状态；尝试将补偿链离散为微段，对每一个微段链条建立动态补偿链的平衡方程，通过数值解法[4]对补偿链的动态位置进行求解和分析；然后对悬链线法和数值法的求解结果进行了比较，最后分析了加速度对补偿链动态特性的影响。

1 建立模型

假设以补偿链的悬挂最低点为（0，C），以此为基准建立补偿链的坐标系，轿厢侧和对重侧对应的补偿链悬挂点坐标分别 为（x1，y1）和（x2，y2）。忽略变形和振动等其它因素的影响，取图1中的任一段补偿链微段ds进行受力分析（如图2）。图2中：T为补偿链张力，N；ρ为补偿链密度，kg/m；g为重力加速 度，m/s2；θ为 补 偿 链和水平线的夹角，rad；a为补偿链运行加速度，m/s2；dT、dθ、ds 分 别 为补偿链张力、角度及长度的变化微量。

根据图2的补偿链微段受力图可建立该单元的动态受力平衡方程：

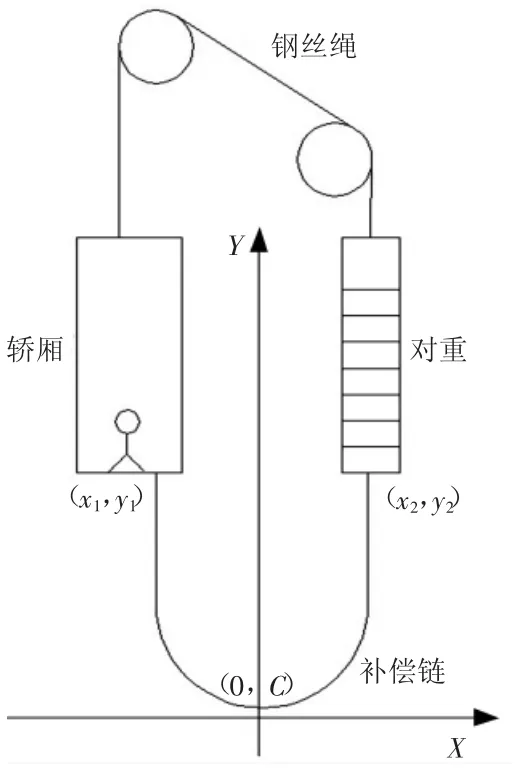
图1 电梯补偿链悬挂图

（T+dT）cos（dθ）=T+ρ·ds·g·sin θ-ρ·ds·a;

（T+dT）sin（dθ）=ρ·ds·g·cos θ。

忽略2阶无穷小微量后，上述方程可以简化为：

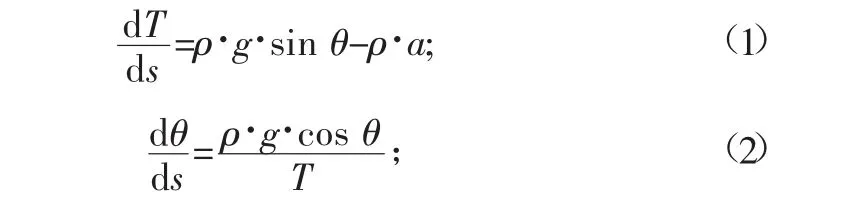
图2 补偿链微段受力图

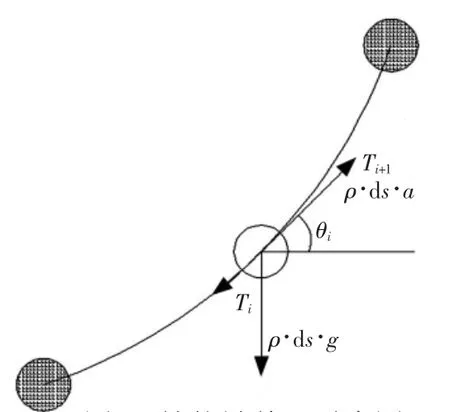
图3 补偿链单元受力图

其中：dx和dy分别为ds在X轴和Y轴方向的分量。

式（1）和式（2）就是求解的控制方程，而通过式（3）和式（4）两个方程就可以求出补偿链的任一点的位置。

2 数值法

2.1 差分格式

对于具体的电梯补偿链来讲，下述条件可设为已知条件：左右悬挂吊点y方向的位置y1和y2、补偿链总长L、补偿链密度ρ、补偿链运行加速度a、左右悬挂吊点的水平距离Lx。现将整个补偿链离散为长度为Δs（即ds）弧段，则总段数N=L/Δs。补偿链的单元受力图如图3所示，这样式（1）～式（4）可以转化为下列差分方程：

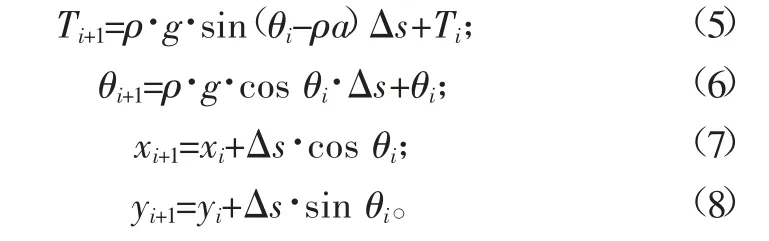
2.2 计算步骤

利用式（5）～式（8）的差分方程，可以采用如下步骤进行补偿位置的计算：

Step1:从最低点（0，C）开始计算。假设此处链条张力初值为T0，C值初始取C0，补偿链和水平线的夹角θ为0 rad。

Step2:按照上述迭代方程（5）～（8）先对右侧的补偿链特性进行计算，

Step3:判断y值是否到达右侧顶点y2：如果y≠y2，则继续进行迭代运算。如果y=y2，则计算x2值，同时保存右侧链条长度L2。

Step4:用右侧相同的T0值和C0值，按照相同的方法对左侧的补偿链进行迭代计算，并判断y值是否已经到达左侧顶点y1。如果y=y1，则同样可以得到x1值，并计算左侧链条长度L1。

Step5:判断（x2-x1）是否达到规定悬挂点距离Lx，如果（x2-x1）≠Lx则修改T0值，并回到STEP1继续进行计算。如果（x2-x1）=Lx则继续下一步。

Step6:判断L1+L2是否等于总弧长L。如果L1+L2≠L，则改变C0值。返回Step1继续进行迭代。如果L1+L2=L则迭代结束。

如此不断地迭代，最终可以获得整条补偿链每一个微段的位置。通过上述数值求解方法就可以得到有加速度的补偿链各单元的具体位置，从而得到整个补偿链的悬挂特性。在迭代过程中取适当的T0和C0值有助于减少迭代运算的时间。

3 实列分析

某曳引乘客电梯采用一根补偿链，该补偿链密度为2.98 kg/m，补偿链悬挂吊点的水平距离为0.35 m，电梯下行加速度为0.5 m/s2，补偿链条总长40.5 m。在顶层、中间层和底层时补偿链悬挂高度如表1所示。

表1 补偿链位置

3.1 数值法和悬链线法比较

图4是分别用悬链线法[3]和数值法求解在加速度a=0 m/s2时的补偿链动态位置曲线图。从图4可以得知，数值法和悬链线法的补偿链悬垂曲线基本一致，在相同高度情况下最大水平距离差异为2 mm左右；因此数值法已经基本能够满足工程上应用的需求。

图4 悬链线法和数值法比较

3.2 补偿链动特性研究

数值法求解的补偿链悬垂曲线如图5所示，其中虚线是a=0 m/s2的补偿链静悬垂曲线，实线是加速度a=0.5 m/s2下行时补偿链的悬垂曲线。由该图可知，补偿链在轿厢加速下行过程中，会偏离静态的悬挂位置，向对重侧偏离。和静态位置相比，带加速度的补偿链最大的偏移距离达到了17 mm左右。由于对称性，当轿厢加速上行时，和静态位置相比，补偿链会向轿厢侧偏离。

图5 补偿链动静态悬垂曲线

4 结语

本文对加速情况下的电梯补偿链的求解方法进行了探讨，对曳引电梯的补偿链进行了离散，并建立了基于差分方程的数值求解方法。在此基础上，对分别用悬链线法和数值法求解得到的静态补偿链位置并进行了分析，得到的表明，数值解法结果和悬链线法结果基本一致。利用数值法求解出有加速度情况下的补偿链悬垂曲线，相对于静态悬垂曲线，有加速度的补偿链会向轿厢或对重侧偏离。因此在设计补偿链周围部件时，需要根据补偿链的动态特性进行设计，防止相关的井道部件和补偿链发生钩挂，防止电梯发生事故。