协作机器人的运动学误差模型及标定算法

任彤，骆敏舟,，张佳丽

(1. 河海大学 机电工程学院，江苏 常州 213022；2. 江苏集萃智能制造技术研究所有限公司，江苏 南京 211800)

0 引言

随着机器人技术的提高与发展，智能机器人辅助、扩展及代替人类智能变成现代机器人技术发展的研究热点。相较传统工业机器人独立的工作方式，人机协作领域的广泛应用使协作机器人成为研发的前沿方向，而机器人的运行精度是描述其工作性能的重要指标之一。为了解决协作机器人重复定位精度优于绝对定位精度的共性问题，提高机器人绝对定位精度成为十分紧迫的任务。

绝对定位精度是指机器人运行到指定路点时目标位姿与期望位姿的精度偏差。针对人机协作的复杂应用场景，机器人运行轨迹不能简单地通过示教方式实现，而是基于其他路径规划辅助工具，生成机器人运行过程中的工作位姿和轨迹，通过与机器人控制器的通信，控制实际运行姿态。除了在线规划场景外，为实现对复杂路径或重复路径应用场景的高效作业，机器人通常采用离线编程方式完成相关任务的路径规划，生成可执行代码程序导入控制机。上述作业的顺利实现均要求机器人有高的绝对定位精度，若无法控制绝对定位精度，在作业过程中则无法实现预先设定的位姿轨迹，在人机协作要求较高的作业环境下，易引发事故。

为提高机器人绝对定位精度，一般采用误差预防法和参数标定法两种方式[2]。误差预防法是指通过提高机器人的加工、装配和控制精度，以控制实际参数与理论运动学参数间的误差量来保证机器人定位精度。除了上述影响因素外，在机器人长时间运行过程中，机械结构发生的磨损与环境影响等原因[2]，各关节运动参数误差传递到末端将严重影响末端运动精度。因此常用参数标定法辨识机器人实际运动学参数[3-5]，通过修正控制器中几何参数的方式提高绝对定位精度。

1 运动学模型建立

首先分析机器人的模型结构与几何参量，在1951年由DENAVIT J 和HARTENBERG R S[6]提出一种命名为D-H参数法的标准空间连杆机构的坐标构建方式，并在机器人领域中广泛应用。各连杆间的位姿关系可通过杆长a、偏置d、杆扭转角α和关节转角θ四个参数确定，通过这四个参数描述杆件的自身集几何参数和与相邻连杆的空间关系[7]。基于D-H参数法，即可确定机器人相邻各连杆间的变换矩阵，建立运动学模型。

(1)

根据机器人设计的相应臂长和零位构型，分别如图1(a)和图1(b)，按照D-H建立关节坐标系，获得机器人D-H参数，如表1所示。

图1 机器人实际臂长与D-H零位构型

表1 D-H 参数表

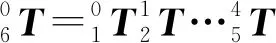
(2)

式中：n为法线矢量；o为方向矢量；a为接近矢量；n、o、a为相互垂直的正交单位矢量。向量p为机械臂末端连杆相对基坐标系的三维位置。

根据上述运动学正向模型与机械臂D-H参数，代入式(2)，可求解机械臂末端的空间位置：

(3)

式中：si和ci分别为sinθi和cosθi的简写形式，i=1，…，6。下文中sinθi和cosθi均以该形式简写，其中正逆解细则可参考文献[8]。

在机器人参数标定过程中，机器人末端位姿的测量值主要用于机械臂几何参数的辨识，同时由于机器人末端位置向量p可反映所需辨识参数ai、αi、di和θi的误差，因此在辨识过程中仅测量末端空间位置，不考虑末端姿态。

2 机器人参数标定

机器人参数标定可分为关节级标定、运动学参数标定和动力学参数标定三个部分[8]。第一部分关节级标定指确定机器人实际关节转动角度与理论转动角度关系，该级精度可通过分析关节理论运行位置与位置传感器信号间的正确关系，测量实际运行中的偏差量获得；第二部分为机器人运动学参数的标定，运动学参数误差包括机器人机构D-H精度，零位标定误差等各连杆间的几何参数误差；第三部分为机器人动力学标定，针对机器人动力学模型误差、各连杆的负载和惯性参数、关节模组柔性机构误差、机构间隙摩擦等各参量进行标定辨识。

考虑各误差参数的可辨识性与误差对绝对定位精度的影响程度，本文在建立误差模型时忽略影响相对较小的因素，同时由于所辨识机器人数学模型为运动学模型，因此主要对第二级机器人运动学参数进行矫正。

根据D-H参数的运动学模型，机械臂末端位置精度依赖于各连杆关节处运动学参数ai、αi、di和θi，而在扭转角αi与机器人整体构型相关不加入误差模型建立，因此基于正解模型，相邻连杆间的位姿微小偏差可被Δai、Δdi和Δθi描述。运动学模型建立的基础上，利用微分运动的思想，求解相邻连杆间的误差矩阵，通过齐次矩阵的连乘计算末端的运动学误差模型。

2.1 相邻连杆间位姿误差

已知相邻连杆齐次转换矩阵如式(1)所示，误差项可表达为：

(3)

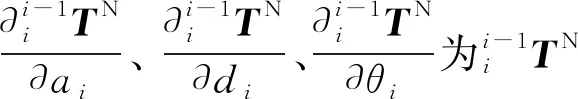
根据全微分定理可得：

(4)

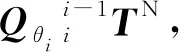
(5)

将式(4)和式(5)代回式(3)中，可得：

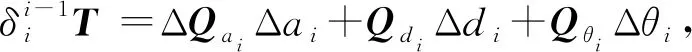
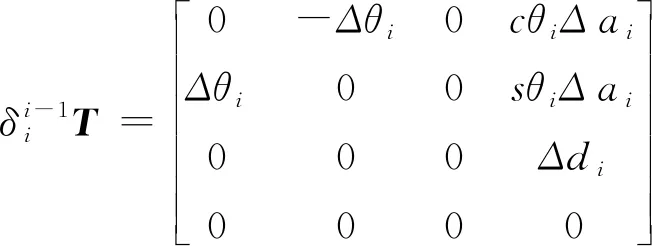
(6)

2.2 微分运动

由于几何参数的误差，末端实际位置与理论位置存在误差，该误差可通过微分运动学描述。微分运动[9]分为微分平移Trans(dx，dy，dz)与微分旋转Rot(k，dθ)两部分，将微分旋转部分分解为绕原坐标系x、y、z轴分别旋转δx、δy、δz，且由于偏转角度为一较小值，因此sinδx=δx，cosδx=1。误差项可由微分旋转矩阵表示为：

TR=TN+dT=Trans(dx,dy,dz)Rot(x,δx)Rot(y,δy)Rot(z,δz)TN

定义ΔT=Trans(dx, dy, dz) Rot(k, dθ)-I4,得

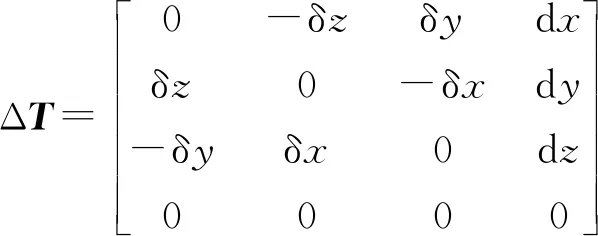
(7)

微分变化ΔT由平移矢量dp和旋转矢量δk组成，同时将式(6)代入可得：

(8)

(9)

(10)

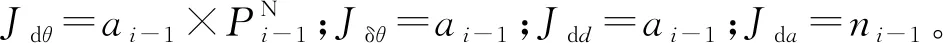
2.3 运动学误差模型

建立精准完善的误差模型是机器人几何参数辨识的重要前提。搭建的机器人标定平台如图2所示。

图2 机器人标定平台

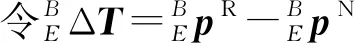
(11)

其中Δa1、Δa4～Δa6、Δd2、Δd3为无需辨识参数，另其系数项为0。

3 实验

运动学参数辨识是将机器人末端位姿误差作为输入量，通过误差模型进行参数的曲线拟合。典型的测量方法包括伸缩式球杆仪[10]、光学跟踪法[11]、激光跟踪仪[12]、平面约束法[13]等多种。本实验为测量末端误差，将机器人安装在有孔的硬板上，安装位置和基座坐标方向与标定板零位重合，实现无外部传感的标定方式，根据所设计的标定板(图3)，可进行两种方式的校准：

1)根据标定板各个位置点信息，将机器人移到正确位置，使工具末端与标定板槽口对齐，假设底面平行且完全重合，以此确定工具末端中心在世界坐标下的绝对位置。

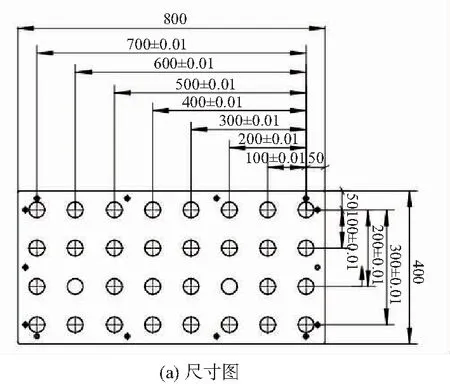
图3 标定板尺寸与实物图

2)安装如图2所示的机器人末端尖端，移动机器人令工具末端尖端与标定板上所安装的尖端完全重合，由于所安装尖端尺寸与工具末端尺寸已知，即可获得工具末端中心在世界坐标下的绝对位置。以上两种校正方式均要求较高精度，在进行曲线拟合前，需注意生成的统计数据，以免影响校准精度。

本实验采用第二种校准方式，控制机械臂在不同的姿态下触碰标定板上的尖端，通过尖端完全重合来保证工具末端位置不变，姿态变化不影响计算精度，记录20组数据，记录各组所对应的机械臂各关节编码器值。

将这20组点依次进行运动学正解，获得在初始化参数下各点对应的末端理论位置值。得到的末端执行器在相对世界坐标系下的实际位置与目标位置的误差如图4所示。

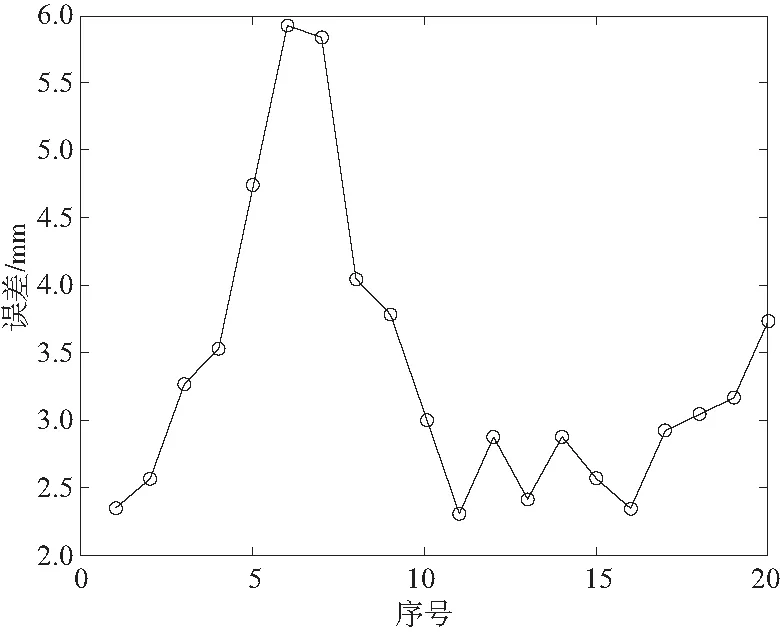
图4 标定前各组数据误差

补偿前机器人工作末端的绝对定位误差平均误差为3.365 mm，其中最大值误差为5.923 mm。根据实际误差将其系数矩阵行奇异值分解，利用最小二乘法对机器人几何参数误差进行辨识，根据式(11)求解运动参数误差值，结果如表2所示。

表2 修正后D-H 参数表

机器人误差补偿的主要方式分为两种，针对控制器开放的机器人通过修改控制器中底层模型运动学参数的方式实现，针对不开放控制器的机器人可通过外部补偿方式，将辨识后的真实参数写入，根据新的运动学模型通过正运动学重新计算优化后的机器人末端位置参数，与实际位置进行比较，结果见图5。

图5 标定后各组数据误差

补偿后工作末端的绝对定位误差平均为1.689 mm，其中最大值为3.512 mm。通过图4与图5对比可得，经过对机器人几何参数的补偿，其绝对定位精度得到了明显的提高，但在数据处理时可发现第6、第7两组数据误差较大，影响参数辨识。因此在数据处理时将这两组数据忽略，重新计算可得表3、图6数据。

表3 数据处理后标定D-H 参数表

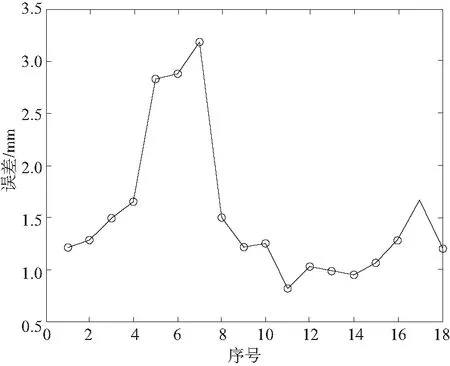
图6 数据处理后各组数据误差

经过数据剔除后，工作末端的绝对定位误差平均误差达到1.528 mm，其中最大值为3.182 mm，由此可得本运动学参数标定方法受输入数据精度影响，并非所有的校准都是好的校准，在标定时应注意生成的统计信息。若输入数据误差太大，机器人标定后的绝对定位精度可能会变得不准确。

4 结语

本文主要研究了六自由度协作机器人的运动学参数标定方法及过程，分析绝对定位精度误差来源，建立机器人微分方程，提出基于机器人工具末端的运动学误差模型建立方法，利用标定板获取机器人工具末端位置信息误差，采用最小二乘法求解误差方程。结果表明该补偿方式可提高绝对定位精度，由补偿前的3.365 mm降为补偿后的1.528 mm。