基于新型负载转矩脉动观测器的滑模控制

张志锋，栾 鹏

(沈阳工业大学 电气工程学院，沈阳 110870)

0 引 言

在伺服系统中，对永磁同步电机的控制精度要求较高[1]，在恒负载或负载变化较小的永磁同步电机调速系统中，采用PI调节器的双闭环矢量控制策略，可满足转矩脉动小、控制精度高的要求[2-3]。但若伺服系统运行在负载变化较大及外部扰动属于不匹配扰动的工况下时，传统方法无法达到理想控制效果。相对于常规的PI控制方法，滑模变结构控制对系统参数摄动、外界扰动及数学描述不准确具有较好的鲁棒性，算法简单，易于工程实现[3-4]。但由于切换开关的时间延迟和状态检测的误差之类的因素，系统存在高频抖动现象，这种高频抖动直接影响到伺服驱动系统高精度控制要求。因此，通过削弱高频抖动来降低转矩脉动是实际应用中必须解决的问题，也是当下滑模控制研究的重点[5]。

目前，削弱高频抖动的方法主要有边界法、趋近律法、滤波法、扰动观测器法及与其它控制论结合的方法。文献[6]采用一种可变边界层准滑模策略，即系统状态先到达较大的边界层，当误差减小至一定值时，切换至小边界层，削弱抖振。但对大边界层和小边界层的设计依据及方法并未给出。当边界层选择过小，系统会因达不到设计边界，导致整体脉动偏大，甚至失稳；当边界层选择过大，系统静态误差变大，降低了系统的鲁棒性。文献[7]提出了一种基于条件积分器的永磁同步电机位置和速度跟踪滑模控制(以下简称SMC)设计，利用条件积分作用(在边界层内)的连续SMC来实现永磁同步电机速度环的渐近误差调节，可部分削弱高频抖动。但积分作用对高频抖动的抑制有限，且此种方法只对恒定负载或瞬态负载转矩变化不大的伺服系统高频抖动有一定的削弱作用。文献[8]提到了一种基于新趋近律的转速控制器，能在一定程度上削弱抖动。但此种方法增加了系统控制的复杂性，且对不匹配的外界干扰所引起的转矩脉动仍无法削弱。而直接采用滤波法滤除高频脉动时，滤波器时间常数的存在会产生较大的相位延迟。文献[9]提出周期扰动观测器对伺服系统重复运动中的周期扰动进行补偿，此种方法能保证系统渐进稳定，同时削弱部分高频抖动，但只对周期性扰动下的转矩脉动有抑制效果。文献[10-11]都利用转矩观测器结合前馈补偿的方法，对高频抖动进行抑制，但伺服系统运行在变负载工况时，并未提到前馈补偿的补偿量如何形成。文献[12]把转动惯量在线辨识加入到滑模观测器中，实现对负载变化下转矩量的补偿，由此提高伺服电机控制精度。但此处转动惯量的辨识以自适应算法理论作为基础，计算量大；而滑模观测器的鲁棒性较强，但观测精度不高，引入转动惯量在线辨识会间接影响系统的稳定性。文献[13]提出新型离散比例-积分滑模，复合速度控制形式与最小阶扰动估计器形成二自由度来削弱高频抖动。但是对于此复合控制形式，需要重新设计超平面，设计复杂。

目前，对SMC下高频抖动的研究已经取得了一定成果。其中，在因外界不匹配干扰引起转矩脉动的研究中，多采用基于扰动观测器的前馈补偿方式来抑制转矩脉动。大多数学者针对恒负载系统，从不同角度设计了各类扰动观测器，并对其进行了深入研究。也有部分学者考虑到不匹配扰动对变负载系统的影响，在变负载系统中，利用负载变化会映射到转动惯量变化的特点，通过以不同算法为核心的转动惯量辨识方法，求得负载转动惯量，将其值加入到扰动观测器中，实现对不匹配扰动下转矩脉动的抑制。总体来说，当前扰动观测器的设计与研究，理论性较强，不易在工程上实现。

本文针对SMC策略下存在周期性转矩脉动的特点，提出一种新型转矩脉动观测器。首先，对转矩观测值进行降噪滤波，通过三点取样法得到较稳定的负载转矩，再将观测值与稳定值做差，即可从转矩观测值中剥离出所需转矩脉动量，以此形成前馈补偿所需的补偿量，最后进行前馈补偿。此种方法既可对恒负载系统进行前馈补偿，也可对变负载系统进行前馈补偿，且不依赖转动惯量的辨识，避免辨识算法涉及到的冗杂计算，大幅减小计算量，易于工程实现，设计简单，对SMC策略的转矩脉动有着较好的抑制效果。

1 SMC原理及控制特点

1.1 SMC理论依据

永磁同步电机控制方式采用按转子磁链定向的矢量控制。含积分环节的SMC以传统SMC作为理论基础，对SMC原理及数学模型不再赘述，仅对滑模控制器的表达式进行简述。在采用指数趋近律的SMC下，令id=0，定义滑模面函数：

s=cx1+x2

定义永磁同步电机状态变量：

式中：ωref为电机给定角速度；ω为机械角速度。

可得q轴参考电流表达式：

式中：p为极对数；φf为永磁体磁链；J为转动惯量；dτ为积分算子。

从q轴参考电流表达式可以看出，由于控制器包含积分项，一方面可以削弱抖动，另一方面，也可以消除系统稳态误差，提高系统的控制品质。

1.2 SMC转矩波形及其特点分析

无论在何种扰动下，系统采用SMC策略，开关函数的存在使状态变量在-ε和ε上来回切换，反映到转矩量则为周期性转矩脉动波形，图1为SMC转矩脉动波形示意图。

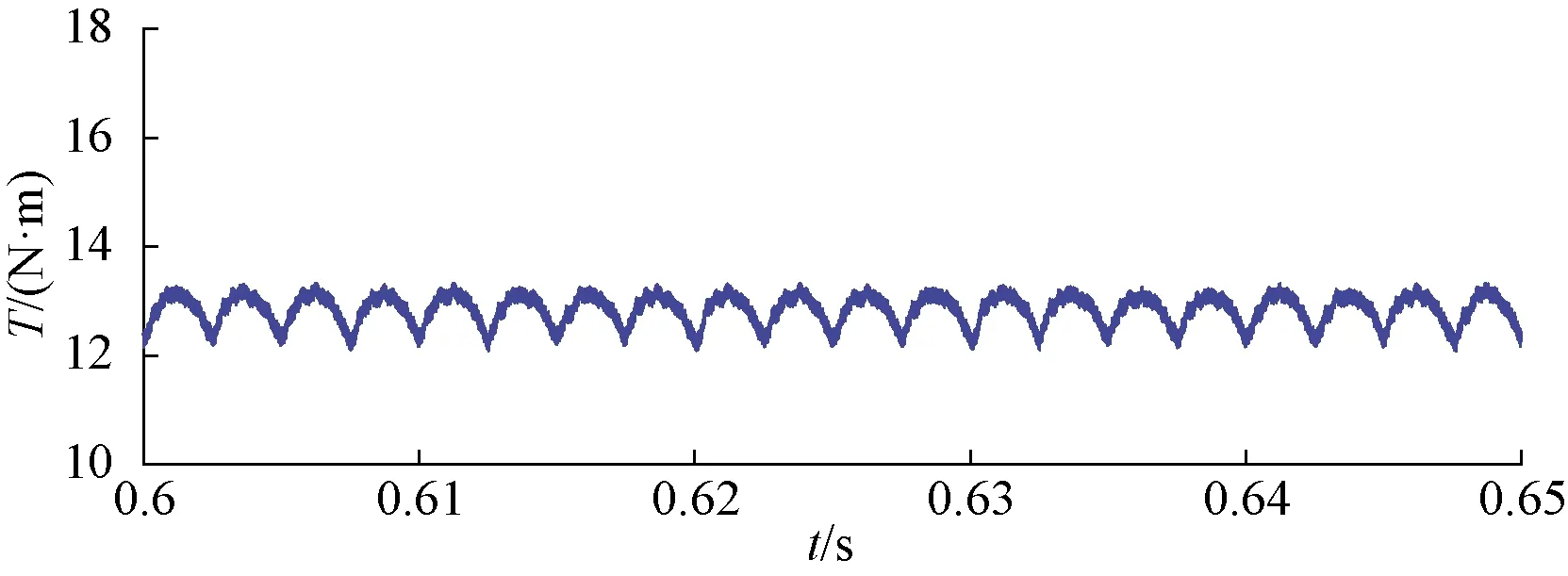
图1 SMC的转矩脉动波形示意图

从控制角度而言，SMC采用开关函数，结合SMC原理可知，在系统稳定的情况下，调节SMC参数不会对脉动波形及其脉动周期产生影响，转矩量的脉动周期较为固定。

2 负载转矩观测器的构建

2.1 转矩观测器的理论依据

以表贴式永磁同步电机作为研究对象，采用id=0的控制策略，其转矩方程：

永磁同步电机的运动方程：

式中：ω为机械角速度；p为极对数；φf为永磁体磁链；Te为电磁转矩；TL为负载转矩；J为转动惯量。

电机内部参数φf、p、J皆为定值，结合永磁同步电机转矩方程和运动方程，可利用电流值iq和机械角速度ω构成对负载转矩的观测。

2.2 负载转矩观测器模型的构建

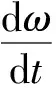
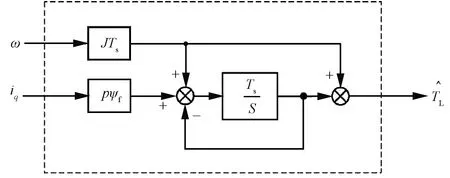
图2 含滤波环节的负载观测器结构框图

高频噪声的频率较高，使时间常数较小的低通滤波器设计得以实现。因此，在对伺服系统高频段噪声滤波处理中，低通滤波器的时间延迟对整体系统的影响较小。

3 负载转矩脉动量的提取

上节转矩观测器可实现对负载转矩的观测，然而，前馈补偿量是以负载转矩脉动量为基础形成的。利用滤波器提取转矩量时，为满足转矩量稳定性要求，其时间常数设定会很大，形成较大的补偿延迟，会对整体系统的稳定性产生影响。

鉴此，提出利用采样取值法直接得到采样点，进而利用采样点配合小时间常数滤波器得到稳定转矩量，通过仿真尝试，发现利用三点取样法，在2倍的基频周期内，等时间采样3次，可得到波动较小的转矩值。

利用三点取样法得到的采样值并不一定为转矩均值，因此，可设定修订系数Ka对其矫正。又因计算后形成离散点，可利用保持器将其变为连续量。而不确定扰动引起的转矩突变会映射到保持器，造成保持器输出结果的突变，因此，加入时间常数较小的低通滤波器，即可得到连续的较低脉动输出均值。为平衡反馈通道中低通滤波器的小幅延迟效果，在前馈通道中加入一个同等时间的惯性环节，即配合滤波环节。而对脉动补偿量参数Kb(Kb<0)的设定，既可使脉动量转为脉动补偿量，也可对补偿量进行调整。新型扰动观测器的输出会因转矩的瞬变过程，导致脉动补偿量的值出现暂态过高现象，因此，在扰动观测器输出前，加入限幅环节，在负载突变时，限制系统因渐进稳定而出现的输出脉动量过大，也有利于改善整体伺服系统稳定性。数据离散点及配合小时间常数滤波器输出波形可见仿真验证。转矩脉动量提取结构框图如图3所示。

图3 转矩脉动量提取结构框图

4 仿真验证

对提出的新型扰动观测器前馈控制算法进行仿真验证。转速环采用SMC，电流环采用PI调节器，优化方式采用前馈补偿策略来抑制转矩脉动。整体系统控制框图如图4所示。

图4 系统控制框图

利用三点采样法得到离散数据点，零阶保持器将离散点变为连续图象，再采用低通滤波器进行平滑处理，得到已削弱脉动量的负载转矩均值。转矩采样及提取图如图5所示。

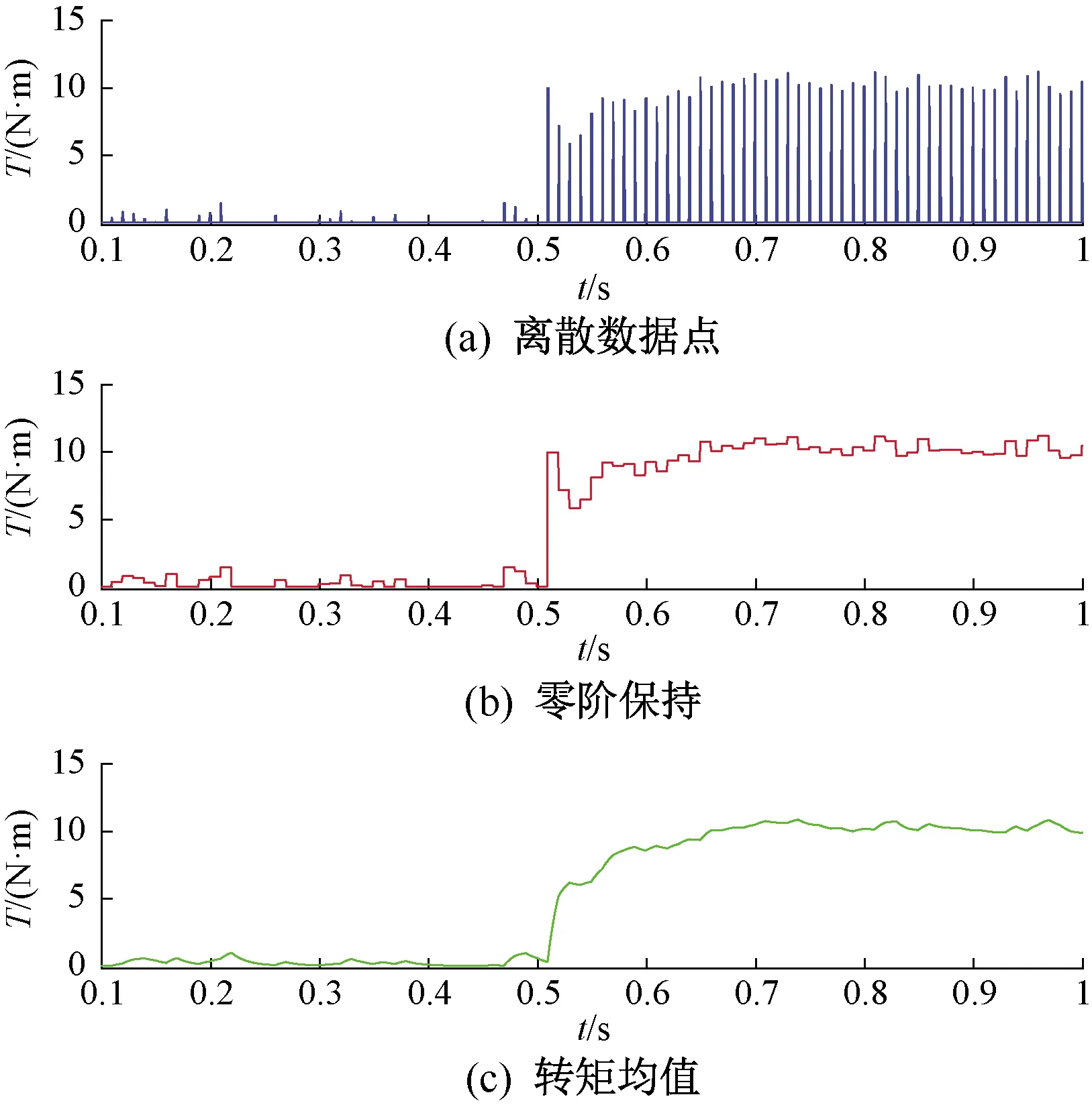
图5 稳定转矩采样提取图

为突出负载转矩脉动量观测器的优势，将其与改进趋近律的SMC进行比较。改进趋近律以指数趋近律为基础，将开关函数改进为反正切函数，此趋近律可抑制转矩小幅脉动。图6为传统SMC、改进趋近律SMC及基于转矩脉动量前馈补偿的伺服系统转速波形对比图。可以看出，补偿策略的转速较为稳定。从起动到空载过程中，转速略有超调，但在0.1 s内迅速恢复。图7为转矩瞬态变化下三种策略的系统转速局部波形对比图。在负载突变的暂态过程中，转速略有降低，但在0.15 s内迅速恢复，响应速度快。

图6 转速对比图

图7 转速局部图

图8为采用转矩脉动观测器前馈控制下伺服系统三相电流波形图。从空载起动到加载运行，整体电流波形为较理想的正弦波，在0.5 s时刻转矩突变时，三相电流波形未出现失真，并在0.15 s内迅速恢复至带载运行所需幅值。

图8 转矩脉动量补偿的三相电流

图9为传统SMC、改进趋近律SMC及基于转矩脉动量前馈补偿的伺服系统电磁转矩对比图。可以看出，无论是在空载情况下还是在带载情况下，基于转矩脉动量前馈补偿伺服系统的转矩脉动都得到了明显抑制。图10为三者的电磁转矩局部对比图。在负载突变的暂态过程中，并与改进趋近律的SMC比较来看，本文优化控制方案在外部不匹配扰动引起负载突变的工况下，电磁转矩的脉动幅度有明显减小，并且伺服系统可在0.1 s迅速进入带负载系统的稳态中，满足伺服系统响应速度快、稳态精度高的要求。将带载转矩波形放大得到图11。当负载为10 N·m时，改进趋近律的SMC转矩脉动范围为10.44～11.35 N·m，脉动量补偿的系统转矩脉动范围为10.46～11.25 N·m，转矩脉动幅度削弱了13.2%，当空载时，改进趋近律的SMC的转矩脉动范围为5.40～6.29 N·m，脉动量补偿的系统转矩脉动范围为5.47～6.27 N·m，转矩脉动幅度削弱了10.1%，验证了基于改进观测器的前馈补偿有较好的转矩脉动抑制效果。

图9 转矩对比图

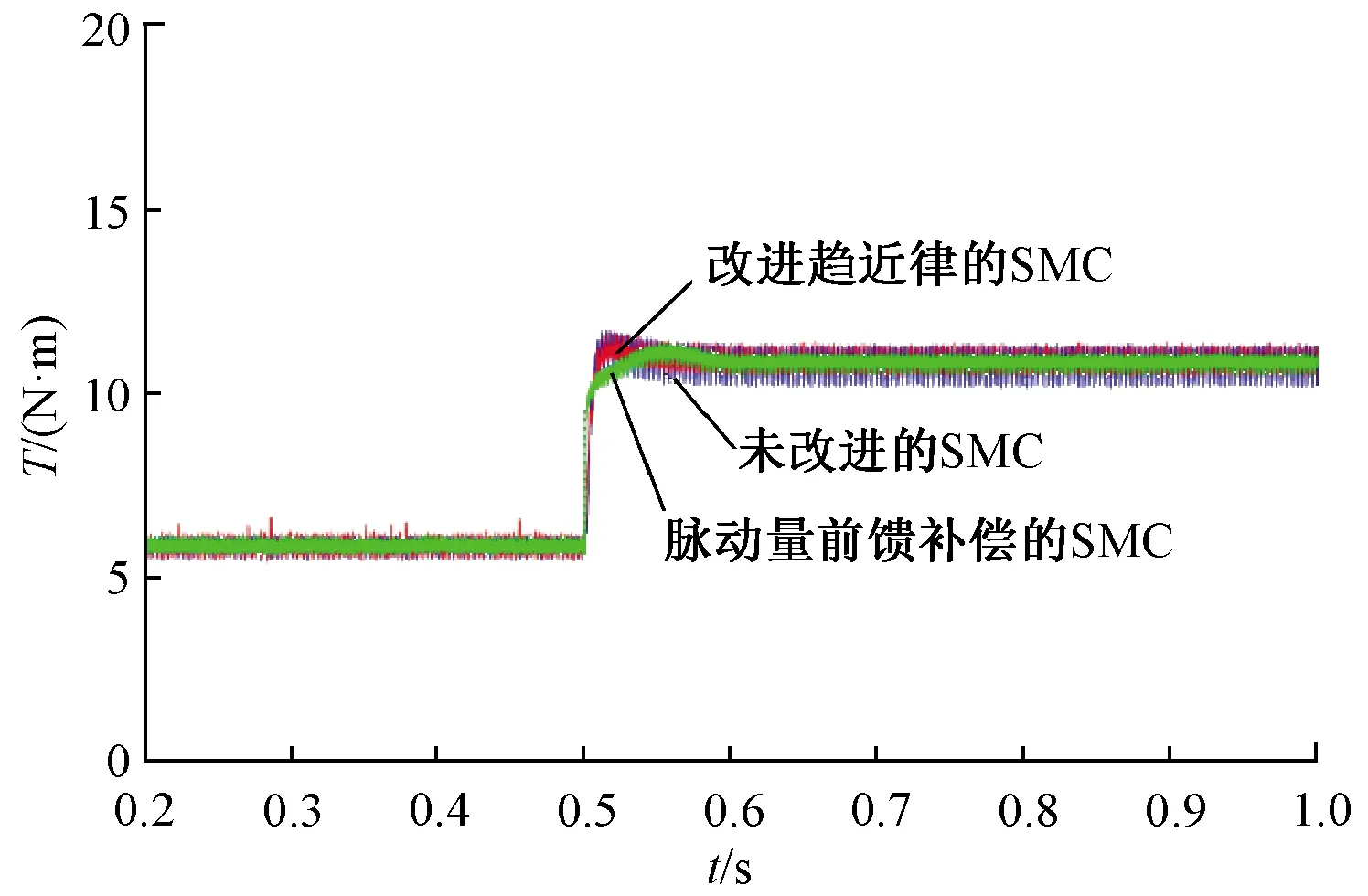
图10 转矩局部图

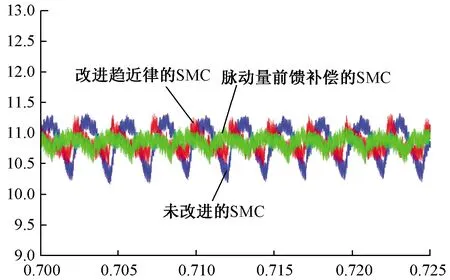
图11 三者转矩局部放大图

5 结 语

SMC下负载转矩具有周期性脉动的特点，针对此特点，提出三点采样法；同时，摒弃了依赖各种冗杂算法的转动惯量辨识法来识别负载转矩变化情况，从负载观测值中分离提取转矩脉动量的角度出发，设计了新型转矩脉动观测器；利用修正系数可将脉动量转为补偿量，也可调控补偿量的多少，进而对负载转矩脉动进行前馈补偿。仿真结果表明，本文的基于新型负载转矩脉动观测器的SMC，对负载转矩脉动有较好的抑制效果，且易于工程实现，证明了利用新型转矩脉动量观测器抑制转矩脉动的方法具有一定的可行性。与此同时，三点取样法为补偿周期性转矩脉动及其他量脉动提供了新思路。