用于酵母细胞电阻抗检测的集成微电极阵列微流控芯片的有限元仿真研究*
2021-05-21钊耿杨烨朱
张 钊耿杨烨朱 真
(东南大学电子科学与工程学院,江苏南京 210096)
近年来,随着多学科交叉的深入发展及微纳加工技术的进步,微流控技术在生命科学、医学检测领域得到广泛应用[1-3]。由于微流控芯片具有小型化的特点,特征尺寸与细胞尺度相近、成本低、结构设计灵活且易于与其他检测分析手段集成,因此被广泛用于单细胞分析[4-6]。酿酒酵母(Saccharomyces cerevisiae),也称为出芽酵母,作为一种重要的模式生物,在现代生物学研究中具有重要意义。而微流控芯片则为酵母单细胞分析提供了便捷又精准的研究平台。
目前,微流控芯片中酵母细胞的监测方法主要是光学显微成像技术[7-9]。通过高分辨显微镜能够获得出芽酵母单细胞的形态、尺寸、生长速率、子细胞剪切等信息。利用荧光蛋白标记亚细胞结构(液泡、细胞核、线粒体等),还能获得酵母细胞内部结构的动态变化[9]。然而,高分辨率时序显微成像技术的通常需要荧光标记,对细胞的正常生理过程存在一定的影响;此外,大批量的图像处理耗时耗力[10]。
相比于显微成像技术,电阻抗谱(Electrical impedance spectroscopy,EIS)具有非侵入性、无需荧光标记、快速检测、多参数读取等特点[11-13]。电阻抗谱检测功能可通过微电极集成在微流控芯片中,通过检测单细胞的介电特性表征细胞尺寸、生长状态等。例如,Haandbaek 等[14]在微流控芯片中集成微电极,并根据电阻抗信号对流经微流体通道的酵母细胞的出芽状态进行区分。Zhu 等[15]提出一种可以捕获酵母单细胞的微流控芯片,并通过电阻抗对单个出芽酵母的生长及运动进行监测、区分。然而,现有的研究成果还无法实现对出芽酵母的高通量、长时间的EIS 监测。因此,用于出芽酵母长时间培养、原位时序电阻抗监测的高通量微流控芯片尚待研究。
本研究提出一种集成高通量酵母单细胞捕获结构及微电极阵列的微流控芯片,建立微流控芯片及酵母细胞的三维有限元模型,分析模型内电流分布情况以及不同行列间距下邻近细胞对于待测细胞EIS 信号的影响。考虑到阵列集成度及检测灵敏度的需求,根据仿真分析结果探索微电极阵列的最优行列间距,对基于电阻抗谱的微流控酵母检测芯片的设计优化具有重要意义。
1 原理和方法
1.1 微流控芯片的结构及工作原理
如图1(a)所示,微流控芯片由玻璃衬底、铬-金微电极阵列、氮化硅绝缘层、SU-8 光刻胶捕获-剪切结构等组成。微电极阵列是酵母细胞EIS 检测的核心结构。如图1(b)、图1(b)所示,微电极阵列由列电极(红色部分)和行电极(蓝色部分)交叉排列而成,SU-8 捕获-剪切结构则分布于每个行列电极交叉处。所有行列电极宽度均为10 μm。列电极与行电极表面有一层氮化硅绝缘层,在捕获-剪切结构上下游分别形成长为15 μm,宽为8 μm 的圆角矩形开孔,用于对出芽酵母的电阻抗检测。氮化硅绝缘层能够有效避免微电极阵列间的电流串扰,提高电阻抗检测的灵敏度。每个捕获-剪切结构以及与之对应的绝缘层开孔处的微电极对即为一个酵母细胞的捕获检测单元。相邻捕获检测单元的列间距设为Δx、行间距设为Δy。如图1(b)、图1(c)所示,捕获-剪切结构由2 根对称的SU-8 微柱组成,微柱高为8.3 μm,2 根微柱的下游开孔宽度为3 μm,与上下游氮化硅开孔距离均为6 μm。图1(c)为捕获检测单元沿AA′的截面示意图,行列电极的厚度均为0.2 μm,氮化硅层的总厚度为1 μm。具体地,列电极位于玻璃衬底表面,行电极位于厚度为0.5 μm 的第一层氮化硅上表面。

图1 微流控芯片几何结构图
如图1(b)所示,出芽酵母细胞以出芽方式进行增殖。母细胞被流体动力固定在捕获-剪切结构中,子细胞在下游开孔外出芽生长,并最终被流体剪切去除。SU-8 捕获-剪切结构、被捕获的出芽酵母细胞以及周围的培养液构成一个等效电路系统,酵母细胞的生长以及子细胞的剪切均会改变系统的电阻抗。通过捕获检测单元上下游的微电极对可以实现对系统电阻抗的检测,其原理是对上游激励电极施加幅值固定的交流电压并记录下游响应电极的电流响应,基于欧姆定律计算出系统的电阻抗[16]。幅值、频率一定的激励信号记为,响应电流记为,则该系统的复阻抗为:
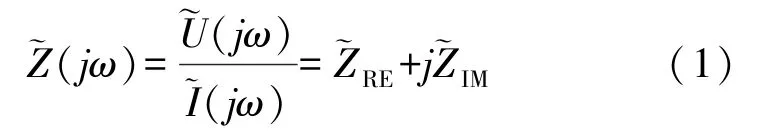
对捕获检测单元中的出芽酵母进行电阻抗检测时,施加激励信号至与之对应的列电极,并检测相应行电极的响应电流信号。按照行列寻址的方式选择不同的行列电极组合,能够实现阵列中所有出芽酵母的电阻抗检测。根据式(1),在激励信号不变的情况下,响应电流的变化能够反映系统复阻抗的变化,进而揭示待测出芽酵母的相关信息,如细胞的尺寸变化、子细胞的剪切等。
1.2 细胞等效模型
出芽酵母细胞具有细胞质、细胞膜、内层细胞壁、外层细胞壁等多层结构,相应结构的几何及材料参数如表1 所示。

表1 出芽酵母细胞多层结构的几何及材料参数[17]
材料的复介电常数和介电常数、电导率的关系如下:

由于用于电阻抗检测的微电极厚度为0.2 μm,远大于细胞膜的厚度(8 nm),直接使用4 层结构的出芽酵母细胞建模时模型中不同结构的尺寸相差过大,会造成网格剖分困难并生成低质单元。基于麦克斯韦混合场理论的均质等效模型被广泛用于模拟多层结构球形细胞的介电性质[18]。应用麦克斯韦混合场理论可将具有细胞膜和细胞质的两层细胞模型等效为一个均质球,其复介电常数为:
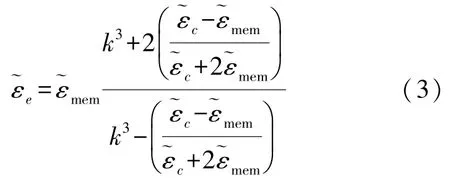
如图2 所示,根据式(3),由内而外逐层进行3次等效,将多层出芽酵母细胞简化成具有等效复介电常数的均质球模型,并根据式(2)计算出等效细胞模型的相对介电常数和电导率,作为有限元模型中细胞的材料参数。

图2 出芽酵母细胞多层结构的均质等效
1.3 有限元模型
考虑到本研究中电极阵列的排布具有周期性以及良好的对称性,根据图1 所示的微流控芯片结构,以2×2、3×3 2 组捕获检测阵列为代表,在COMSOL Multiphysics 软件中建立对应的三维模型进行有限元仿真研究。模型中捕获检测单元的列间距、行间距分别设为全局参数Δx、Δy,便于进行行列间距的参数化扫描。模型中其他结构尺寸参照1.1 节设置。
前期研究结果表明,1 MHz 频率下的电阻抗幅值信号能够较好地反映细胞几何尺寸的变化[19]。因此,我们利用1.2 节的等效模型理论计算1 MHz频率下母细胞和子细胞的等效材料参数,即相对介电常数与电导率。有限元模型中其他各结构的材料参数如表2 所示。
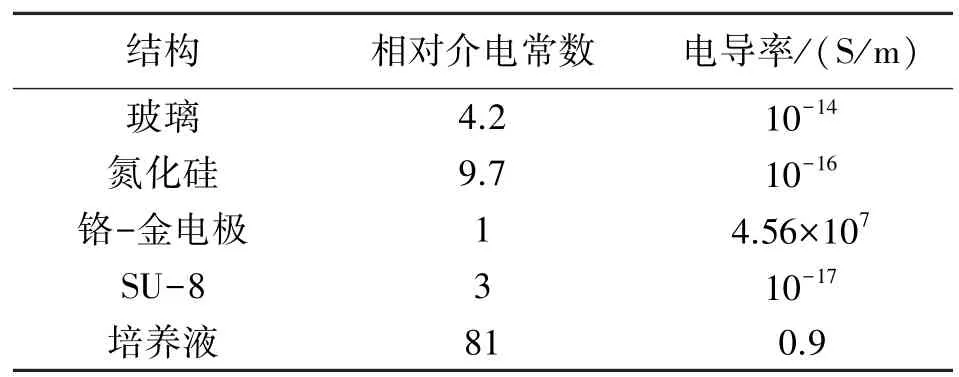
表2 仿真模型结构的材料参数
应用AC/DC 模块的电流物理场对有限元模型进行仿真。仿真模型基于欧姆定律求解电流守恒方程:
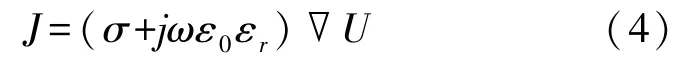
式中:σ为电导率,ε0、εr分别为真空介电常数、相对介电常数,∇U是电势差。
模型的外部边界条件设为电绝缘,内部不同域的交界面设置为电流连续条件,所有域的电势初始值设为0 V。列电极从左到右依次记为S1、S2、S3电极,行电极从上至下依次记为R1、R2、R3电极。仿真中,待测捕获检测单元对应的列电极为激励电极,设置其终端电压为幅值1 V,频率1 MHz 的交流电压;对应的行电极为响应电极。非检测电极设置为初始值为0 V 的悬浮电位或接地。基于电流守恒方程对模型进行有限元求解,并通过全局计算得出待测出芽酵母细胞对应的响应电流。
1.4 仿真计算
本研究中,以待测母细胞的子细胞剪切造成的响应电流相对变化量作为判断电阻抗检测灵敏度优劣的指标。非检测电极不同的设置对待测细胞的检测灵敏度有较大影响,因此需要分别对其设置成悬浮电位和接地进行仿真计算,从而指导后续研究。待测细胞对应的响应电流会受到其邻近捕获检测单元中细胞的影响,其中以是否存在邻近细胞的影响最为显著。因此,在芯片设计时,需选择合适的行列间距以确保邻近细胞的存在与否对待测响应电流的影响远小于目标检测单元中酵母子细胞剪切产生的信号变化,进而通过测得的EIS 信号准确反映子细胞的剪切事件。
为方便表示,将第x行第y列被捕获的出芽酵母细胞记为Cxy。对出芽酵母细胞Cxy进行EIS 检测时,设置Sx为激励电极,Ry为响应电极。进行有限元仿真求解后,计算Ry的响应电流幅值Iy。为便于分析,对仿真结果数据作以下处理:定义待测出芽酵母Cxy被捕获与未被捕获时响应电流幅值Iy的比值为相对幅值Ar。待测出芽酵母细胞的子细胞剪切以及邻近细胞的有无使得相对幅值Ar产生的变化量的绝对值记为ΔAr。
首先仿真分析非检测电极设置悬浮和接地的C11子细胞剪切的检测灵敏度。在阵列大小为2×2的模型中,所有捕获检测单元设有母细胞,设置S1电极为激励电极,R1电极为响应电极。分别将非检测电极设置成悬浮和接地,对行间距和列间距为50 μm、75 μm、100 μm、125 μm、150 μm、175 μm、200 μm、225 μm、250 μm、275 μm、300 μm 的全部组合进行参数化扫描求解。基于每一个参数化解计算ΔAr,分别绘制其关于行列间距的三维柱状图,并对比分析。此外,绘制培养液中电流密度模的体箭头图,分析响应电流I1的组成及分布情况。基于每一个参数化解,绘制响应电流I1关于行列间距的三维柱状图,分析行列间距变化对I1的影响。
进一步研究不同行列间距组合中,单个邻近细胞存在与否造成的ΔAr,并将其与C11子细胞剪切造成的ΔAr作对比,确定较小的行列间距使邻近细胞存在与否造成的ΔAr相对于C11子细胞剪切造成的ΔAr达到最低。在阵列大小为3×3 的模型中,被捕获的母细胞C11为目标细胞,设置S1电极为激励电极,R1电极为响应电极。对行间距和列间距为50 μm、75 μm、100 μm、125 μm、150 μm、175 μm、200 μm、225 μm、250 μm、275 μm、300 μm 的全部组合进行参数化扫描求解,分别研究母细胞C12、C13、C21、C31、C22存在与否以及C11子细胞剪切对响应电流I1的影响。基于每一个参数化解计算ΔAr,分别绘制ΔAr关于行列间距的三维柱状图进行比较。
2 仿真结果与讨论
2.1 非检测电极设置悬浮和接地的EIS 检测灵敏度比较
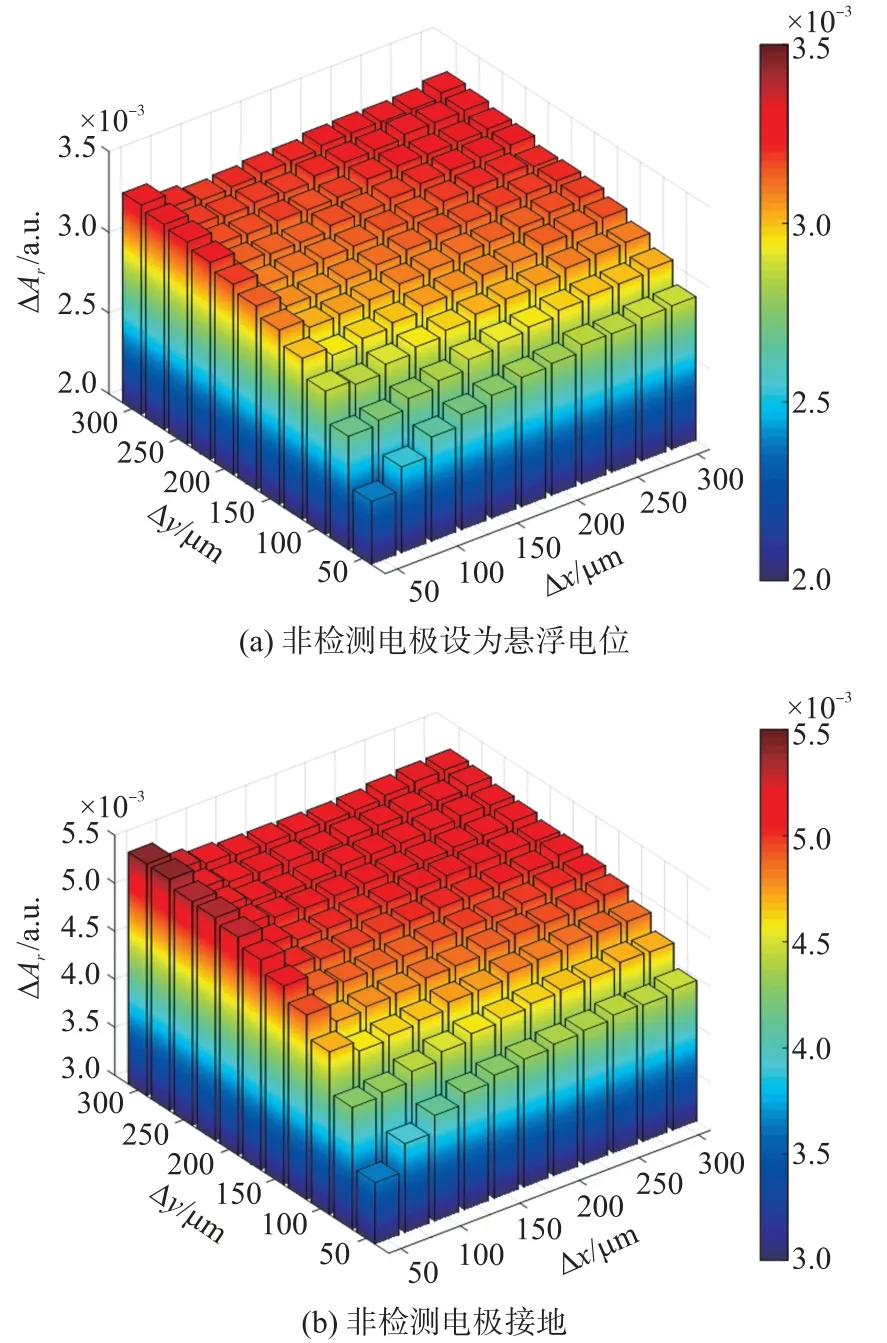
图3 非检测电极的不同设置对C11子细胞剪切的影响
如图3(a)、图3(b)所示,非检测电极设置成悬浮和接地时,C11子细胞剪切造成的ΔAr随行列间距变化的趋势相似,整体上随着行列间距增大而逐渐增大。非检测电极接地时,C11子细胞剪切产生的ΔAr更大,其EIS 检测灵敏度更高。因此,后续的仿真实验中非检测电极均设置为接地。
2.2 响应电流的组成及分布
如图4(a)、图4(b)所示,响应电极R1记录的响应电流I1由4 部分构成,依次记为Ia、Ib、Ic、Id。其中,只有部分Ia流经C11所在的捕获检测单元,因此只有Ia反映母细胞C11的几何尺寸信息。响应电流I1中Ia所占的比重越大,对于母细胞C11的检测灵敏度越高。Ib流经C12所在的捕获检测单元,因此C12细胞存在与否主要影响Ib,进而对响应电流I1造成影响。C12细胞的存在使其所在捕获检测单元处的电阻抗提高,Ib减小,因此响应电流I1减小。C21细胞存在时其所在捕获检测单元处的电阻抗提高,造成Ic、Id增大,因此响应电流I1增大。

图4 响应电流的分布及组成
如图5 所示,总体上,响应电流I1随着行列间距的增大而减小。在行列间距为200 μm~300 μm时,响应电流I1几乎不随行列间距的变化而变化。这是由于此时行列间距已经足够大,Ib、Ic、Id较小,响应电流I1主要由Ia组成,此时对酵母细胞C11的EIS 检测灵敏度较高。

图5 响应电流的幅值变化图
2.3 邻近细胞对响应电流的影响
非检测电极设为接地,仿真研究不同行列间距组合中单个邻近细胞存在与否以及待测子细胞剪切造成的ΔAr。图6(a)~图6(e)分别反映了待测细胞C11的邻近细胞C12、C13、C21、C31、C22存在时响应电流相对幅值ΔAr随行列间距的变化。如图6(a)、图6(b)所示,总体上来看,随着列间距的增大,C12细胞的存在造成了ΔAr显著减小。由于C12细胞主要影响Ib,当行列间距均在100 μm 以下时,Ib在I1中所占比重较小,Ib的变化并未引起响应电流的显著变化,因此ΔAr较小。随着行间距的增大,Ic、Id逐渐减小,响应电流中Ib所占比重逐渐增大,因此ΔAr逐渐增大。C13细胞的存在引起ΔAr的变化相对于C12细胞的存在小一个数量级,因此其影响可以忽略。如图6(c)、图6(d)所示,随着行间距的增大,C21细胞的存在引起ΔAr显著减小。这是由于C21主要影响Ic、Id,随着行间距的增大,Ic、Id逐渐减小,因此ΔAr也逐渐越小。C31细胞的存在引起ΔAr的变化相对于C21细胞的存在小一个数量级,因此其影响也可忽略。如图6(e)所示,C22细胞的存在引起ΔAr的变化比C12、C21细胞的存在小1 到2 个数量级,其影响忽略。待测细胞C11的子细胞剪切引起ΔAr的变化如图6(f)所示。总体上,随着行列间距的增大,C11子细胞剪切的检测灵敏度逐渐增大。
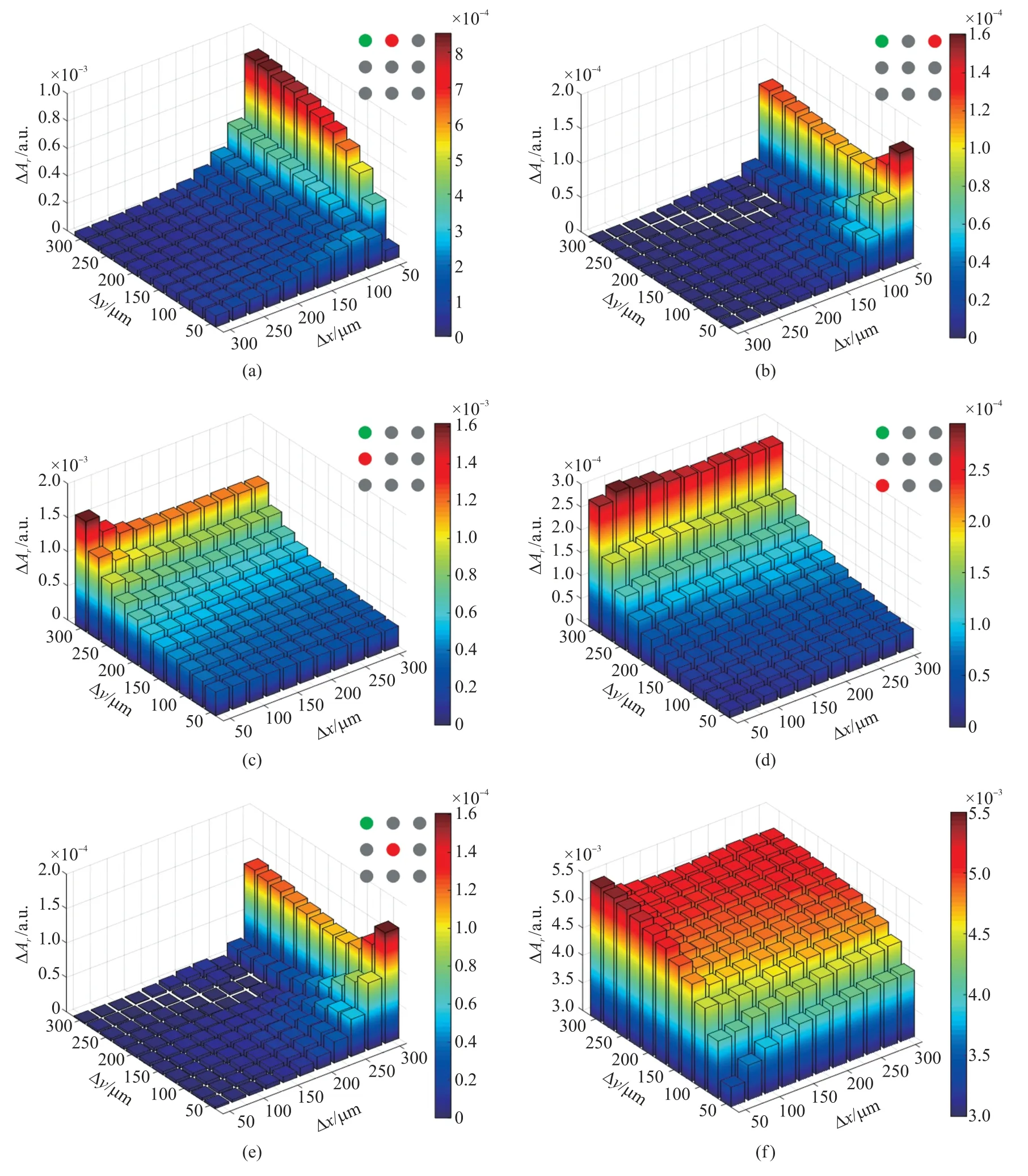
图6 邻近细胞的存在及待测细胞子细胞剪切对待测响应电流的影响
由以上分析可知,与待测细胞同行或同列的邻近细胞对响应电流的影响随着列间距或行间距的增加而显著下降,并且最邻近的细胞对响应电流的影响要远大于较远处的细胞。与待测细胞不同行不同列的细胞对响应电流的影响可忽略。因此在确定合适的行列间距时只考虑C12、C21细胞的存在对ΔAr的影响,分别将其与C11的子细胞剪切造成的ΔAr比较。行列间距越大,邻近细胞对于响应电流的影响越小,目标细胞的检测灵敏度越高。然而捕获检测单元的行列间距过大会降低酵母单细胞的捕获效率以及芯片的集成度。因此,综合考虑检测灵敏度以及芯片集成度,选择列间距为100 μm、行间距为125 μm 作为捕获检测阵列的设计参数。此行列间距下,C12、C21细胞存在与否以及C11子细胞剪切造成的ΔAr分别为1.78×10-4、6.85×10-4、4.66×10-3。与C11子细胞剪切造成的EIS 信号变化(4.66×10-3)相比,邻近细胞对于响应电流相对幅值的影响在其15%以下,因此预期可实现对待测出芽酵母子细胞剪切事件的准确检测。
3 总结
在本研究中,我们提出了可用于出芽酵母细胞电阻抗检测的集成微电极阵列微流控芯片的设计结构,并建立了三维有限元模型,重点研究了微电极阵列的行列间距对细胞电阻抗检测灵敏度的影响。通过有限元模型仿真计算中对捕获检测单元的行列间距进行了参数化扫描,分析了微电极阵列中待测响应电流的分布及组成,并研究了邻近细胞对于待测响应电流的影响,确定了有效检测待测出芽酵母子细胞剪切所需的最小行列间距组合。所提出的集成微电极阵列微流控芯片有望用于基于电阻抗谱技术的高通量酵母单细胞复制衰老及寿命检测,建立的有限元模型及仿真分析结果为微流控芯片的设计及优化改进提供了重要参考。
