1990~2013 年我国省域人口死亡率估计及变动趋势研究①

唐爽 刘乐平 李凤伟

（天津财经大学 统计学院，天津 300222）

1 研究背景

由于经济发展水平、自然地理环境和人文风俗习惯等因素不同，各国（地区）人口死亡水平存在差异，国家（地区）层面上对此问题的讨论由来已久[1-4]，考虑到我国地域辽阔、民族众多，省域分年龄人口死亡率的演变差异同样值得研究。

目前，数据质量最高的省域人口死亡数据，可通过人口普查资料获得，而我国至今仅有六次人口普查，且前两次普查并未注意收集死亡人口信息，因此省域死亡数据时序较短且跨度较大，若采取简单平均的方法估计区间内死亡水平，则默认了人口预期寿命②本文表述若无特殊说明，预期寿命特指新生儿预期寿命。均匀增长的假设，该假设是否合理？真实状况究竟如何？这都需要通过比较严谨的估计测算予以回答。另外，人口死亡数据应用范围不仅局限于人口学，该数据匮乏也会使相关非人口理论在省域层面的研究受到限制[5-6]。

对省域人口死亡状况的讨论并不少见，相关研究按使用数据类型可大致分为两类：一是针对某一次普查资料的单独研究，二是结合几次普查资料的分析。早在1988 年，郝虹生等人利用我国第三次人口普查（简称“三普”）资料，通过模型生命表法对原始数据进行调整修正，对分省死亡率进行了较为系统的分析[7]。路磊等人利用“四普”资料，设法解决时期选择和死亡人口分布的难题，给出1990 年我国分省简略生命表[8]。Congdon 提出一种Bayesian 随机效应模型，利用“五普”分省死亡数据，分析了我国人口死亡状况的空间聚集性和省域差异[9]，杨贵军和刘帅则使用上述模型对“六普”数据分析并与Congdon 的研究进行比较[10]。针对“六普”数据，舒星宇等人利用生命表法和模型生命表法分别计算省域人口预期寿命，发现原始数据往往会高估预期寿命[11]；杨明旭和鲁蓓则利用我国五岁以下儿童死亡率，对省域死亡率修正后计算不同岁组预期寿命并进行分析[12]。结合几次普查资料进行研究，既可考察人口死亡水平的大致变动趋势，又可相互检验不同批次普查资料的数据质量。任强等人认为对不同时点的死亡数据采用统一方法进行调整、修正十分必要，他们结合“三普”、“四普”和“五普”资料，通过假设两次普查间死亡水平具有线性变化，利用内外插补法研究了人口死亡水平的区域差异[13]。刘会敏等人同样利用上述三次普查资料，使用空间统计分析技术，按死亡水平变化趋势，对各省分类后进行讨论[14]。黄荣清基于“四普”和“五普”资料，阐明死亡人口漏报的社会原因，并计算两次普查中死亡人口的漏报程度[15]。王金营则利用“四普”、“五普”和“六普”资料，采用队列留存法和模型生命表法，对这三次普查资料的死亡漏报情况深入讨论，并对死亡率和预期寿命进行重新估计[16]。

虽然我国省域数据相对匮乏，但自1995 年来，全国水平和市镇乡人口死亡数据可从《中国人口和就业统计年鉴》上轻易获取，因此人口死亡率的动态演变在该层面的讨论相对广泛[17-18]，省域层面的研究相对不足，其主要原因之一就是数据不易获取。

本文的工作，即利用Clark 提出的SVD-Comp 模型[19]，通过结合多源相关数据，在统一方法下，同时完成对省域死亡数据的估计补全与数据修正，并进一步分析省域人口死亡规律，希望对相关学术研究和政策制定有所裨益。本文工作还可以从另外两个角度进行归纳：一是死亡数据质量评估与测算，二是死亡率模型的研究与应用。

死亡数据质量评估与测算。拥有可靠数据是进行相关研究的基础，由于死亡数据不易获取和计算，即使是权威数据平台之一的人类死亡率数据库（HMD）③https://www.mortality.org/，其数据质量也会受到质疑[20]。我国数据质量最高的死亡数据即通过人口普查获得，但普查数据却仍含瞒报、漏报等情况[21-24]，个别年龄段数据具有特殊价值，吸引许多学者进行专门测算与修正[25-28]。不同方法对已有数据的估计与修正，有助于理解数据背后的真实状况。

死亡率模型的研究与应用。分年龄死亡率预测有两类代表性方法，一类是模型生命表方法[1][29]，一类是随机死亡率模型[30-31]。两类方法目的相同，但思路和使用情景却不相同，模型生命表法需要有大量已观察到的不同人口死亡数据，从而可对死亡模式进行归纳，这样即使目标人口仅拥有较少信息，仍可通过选择合适的死亡模式进而预测得到分年龄死亡数据；随机死亡率模型则需要目标人口拥有连续时序的分年龄死亡数据，此时不需要依赖其他数据即可完成预测。两类方法各有优势，针对任意一种方法的研究与应用都浩如烟海，本文重点不在此故不赘述，SVD-Comp模型可看作是两类方法的结合，这种做法并不少见，如联合国人口展望项目（WPP）预测死亡率使用的方法[32]，黄匡时则将随机死亡率模型应用于扩展模型生命表[33]。

2 研究方法

本文以Lee-Carter 模型[30]和Log-Quad 模型[29]为例，简介随机死亡率模型和模型生命表法预测死亡率的工作原理，说明SVD-Comp 模型方法[19]如何插补死亡率数据，介绍Kannisto 模型如何修正高龄人口死亡率，并给出所用预期寿命的计算方法。

2.1 Lee-Carter 模型与 Log-Quad 模型

Lee-Carter 模型，作为最早和经典的随机死亡率模型，其形式十分简洁：

其中变量x和t分别表示年龄和时间，m(x,t)为中心死亡率④本文表述若无特殊说明，死亡率特指中心死亡率。，α(x)描述特定年龄人口的平均死亡率水平，k(t)描述分年龄人口死亡率水平，b(x)则描述了特定年龄人口死亡率对k(t)变化的敏感程度。

需要注意的是，该模型等式右边全为待估参数，为解决模型识别问题，通常需要对待估参数施加约束，以得到唯一解：

该模型参数求解方法并不唯一，常见解法包括奇异值分解（SVD）法、最小二乘法和极大似然法等。选择合适方法完成参数求解后，再对参数k(t) 建立合适的时间序列模型进行外推预测，将预测年份tf对应的k(tf) 返带入公式（1），即可得到该年分年龄死亡率预测结果。

Log-Quad 模型，由于随机死亡率模型的使用需要目标人群具有一定连续长度的死亡数据，而大部分发展中国家（地区）的死亡率数据搜集工作往往开始较晚，甚至无法获取分年龄死亡数据，此时仅拥有一些基础的生命指标如：五岁以下儿童死亡率（sq0）、成人死亡率（45q15）、新生儿预期寿命（e0）等，因此Log-Quad 模型具有如下形式：

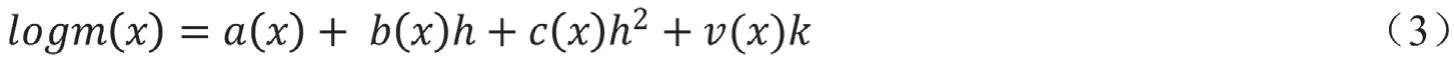
其中x 为年龄，m(x) 为中心死亡率，h为可观测生命指标的对数（如，log(sq0），α(x)、b(x)和c(x)为与年龄有关的二次模型系数，v(x) 是特定年龄的校正因子，k是其系数。

该模型需要已知一定量生命表信息，用于m(x)和h的二次模型拟合，求出参数a(x)、b(x)和c(x)，而v(x)k其实为（logm(x)-α(x)-b(x)h-c(x)h2）SVD 分解后的第一主成分。模型参数完成校准之后，只要给出h 和k，则可计算对应的分年龄死亡率。

两类模型从形式上看都属于广义线性模型，而随机死亡率模型特点是降维处理，其只需目标人群死亡数据；模型生命表类似回归模型，它尝试寻找相关数据与分年龄死亡数据之间关系，故需有一定量多种人群的真实生命表和相关数据信息作为基础。

2.2 SVD-Comp 模型

SVD-Comp 模型使用方法如下：

记Q为A×L的矩阵，矩阵Q由L列相关且同性别人口的分年龄死亡率（对数）合并形成，A是分年龄死亡率岁组的组数，利用SVD 方法对其分解可得：

其中s是由奇异值si从大到小排列形成的对角矩阵，U是左奇异向量ui按列合并形成的矩阵，v是右奇异向量vi按列合并形成的矩阵，ρ为奇异值个数。由于SVD 分解性质，矩阵Q常可用前c个奇异值进行近似。

通过进一步推导，矩阵Q的第l 列向量qt可表示为：

其中vli表示右奇异向量vi中第l个数值，列向量ql即为一组分年龄死亡率数据，当保持si和ui不变时，通过vli数值变动即可得到不同的分年龄死亡率。

将vli与可观测生命指标hl进行拟合建模，hl为分年龄死亡率ql对应的同期数据：

选择合适的fi(·)函数形式完成参数化后，只需将生命指标h带入公式（6），得，与h对应的同期分年龄死亡率即可通过公式（5）获得：

本文后续实证，考虑到所用数据特征和建模效果，参考Clark 的研究方法[19]，公式（6）中的fi(·)函数采用如下形式：

同时发现取前两个奇异值即可完成较好的建模效果，即c=2，iε{1,2}。

2.3 Kannisto 模型扩展高龄人口死亡率

对于我国高龄人口死亡率，由于人口暴露数较少，且瞒报、漏报等情况时有发生，因此本文利用Kannisto 模型对高龄人口死亡率进行扩展修正[12][27]。

有三种常见的死亡指标：中心死亡率mx，死亡概率qx和死亡力ux；三者之间存在联系，也可互相转换，高龄人口中常用死亡力ux建模，Kannisto 模型形式如下：

本文用60—85 岁死亡力ux数据拟合模型，求出参数α和β后，即可完成85 岁以上人口死亡力扩展。三种死亡指标通过以下两式可以转换：

其中，公式（10）是简化sacher 估计；公式（11）参数wx描述了死亡人口的分布情况，本文取wx=0.5，即假设全年龄段上死亡人口在单位时间内是均匀分布的，n表示年龄组距。

2.4 预期寿命计算方法

本文后续由插补所得全年龄死亡率（中心死亡率），根据生命表方法计算新生儿预期寿命e0，其中涉及如下指标：mx中心死亡率，qx队列死亡概率，lx幸存人口数，dx死亡人口数，Lx平均生存人年数，Tx平均生存总人年数，ex平均预期寿命。根据本文估计所得mx，再通过公式（12）至公式（17），依次计算各指标，最终可得到预期寿命：

其中n表示年龄组距，通常一岁一组的情况下（n=1），计算的生命表叫完全生命表，本文所用为简略生命表，其中0 岁组，年龄组据为n=1；1-4 岁组，年龄组据为n=4；其余岁组，年龄组距n=5。

值得说明的是，0 岁组中心死亡率和0 岁组死亡概率（婴儿死亡率）对预期寿命的计算影响较大，且两者通过公式（12）转化时，wx=0.5 的假设不再适用，参考杜本峰和张寓的研究设定[36]，此时令w0=0.3。

3 数据来源及说明

本文所用数据，主要由三部分构成：1990、2000 和2010 年我国人口普查资料⑤http://www.stats.gov.cn/tjsj/pcsj/，人类死亡率数据库（HMD）以及国家卫生健康委员会的妇幼卫生监控（MCHS）⑥http://www.mchscn.org/数据。

人口普查资料。该数据是获取我国省域人口死亡状况的重要来源。1990 年分省死亡率数据本文采用路磊等修正后数据[8]，而2000 和2010 年死亡率数据均由相应普查资料中表6-1（省、自治区、直辖市分性别、年龄的死亡人口）和表1-7（省、自治区、直辖市分性别、年龄的人口）两张表计算所得。其中1990 年最高年龄分组为85+岁组，而2000 和2010 年最高年龄分组为100+岁组。

图1 中国大陆与中国台湾和日本人口死亡模式的对比

HMD 数据库。该库是被广泛使用的死亡率数据库之一，由于在使用SVD-Comp 模型时，仅依赖我国大陆数据无法完成建模，因此使用我国台湾地区（1970~2014 年）和日本（1947~2017 年）的中心死亡率mx 和五岁以下儿童死亡率5q0⑦用于辅助建模。我国大陆、我国台湾与日本的人口死亡模式具有相似性，见图1，且HMD 数据质量较高，利用该数据与我国大陆数据共同建模，在完成数据插补的同时，也能对我国分省数据进行修正。

MCHS 数据。由于五岁以下儿童死亡率5q0与分年龄死亡率密切相关，故本文选用5q0作为生命指标h用于插补省域死亡率数据。MCHS 系统一直跟踪记录我国省域5q0数据，但并未直接公开，Wang 等人利用MCHS 数据估计出1990~2013 年我国省域五岁以下儿童死亡率5q0，并将研究成果通过卫生指标与评估研究所（IHME）⑧https://vizhub.healthdata.org/subnational/china对外公开[25]，此数据也被杨明旭和鲁蓓用于修正“六普”资料中低龄儿童死亡率[12]。

本文使用分年龄数据的年龄分组为五岁一组，考虑到普查数据中我国高龄人口（85 岁以上）死亡率波动性较大，与中国台湾和日本存在明显差异，该部分数据质量仍存在争议，故本文实证SVD-Comp 模型中矩阵Q，仅使用0-85 岁死亡数据联合建模（即，最后一个年龄分组为80-84 岁分组）。预测得到1990~2013 年连续分省数据后，再利用Kannisto 模型对高龄人口死亡率进行扩展，将年龄分组补全至100+岁组。

4 实证结果与分析

4.1 模型拟合效果分析

模型的拟合情况。将分年龄死亡率的模型值与实际普查数值做比较，可以直观看出本文所用方法对数据的拟合效果。其中，SVD-Comp 模型估计85 岁以下的人口死亡率，Kannisto 模型估计85 岁至100+岁的死亡率。

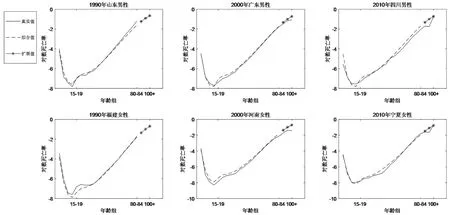
图2 死亡率原始值与模型拟合值和高龄扩展值的对比

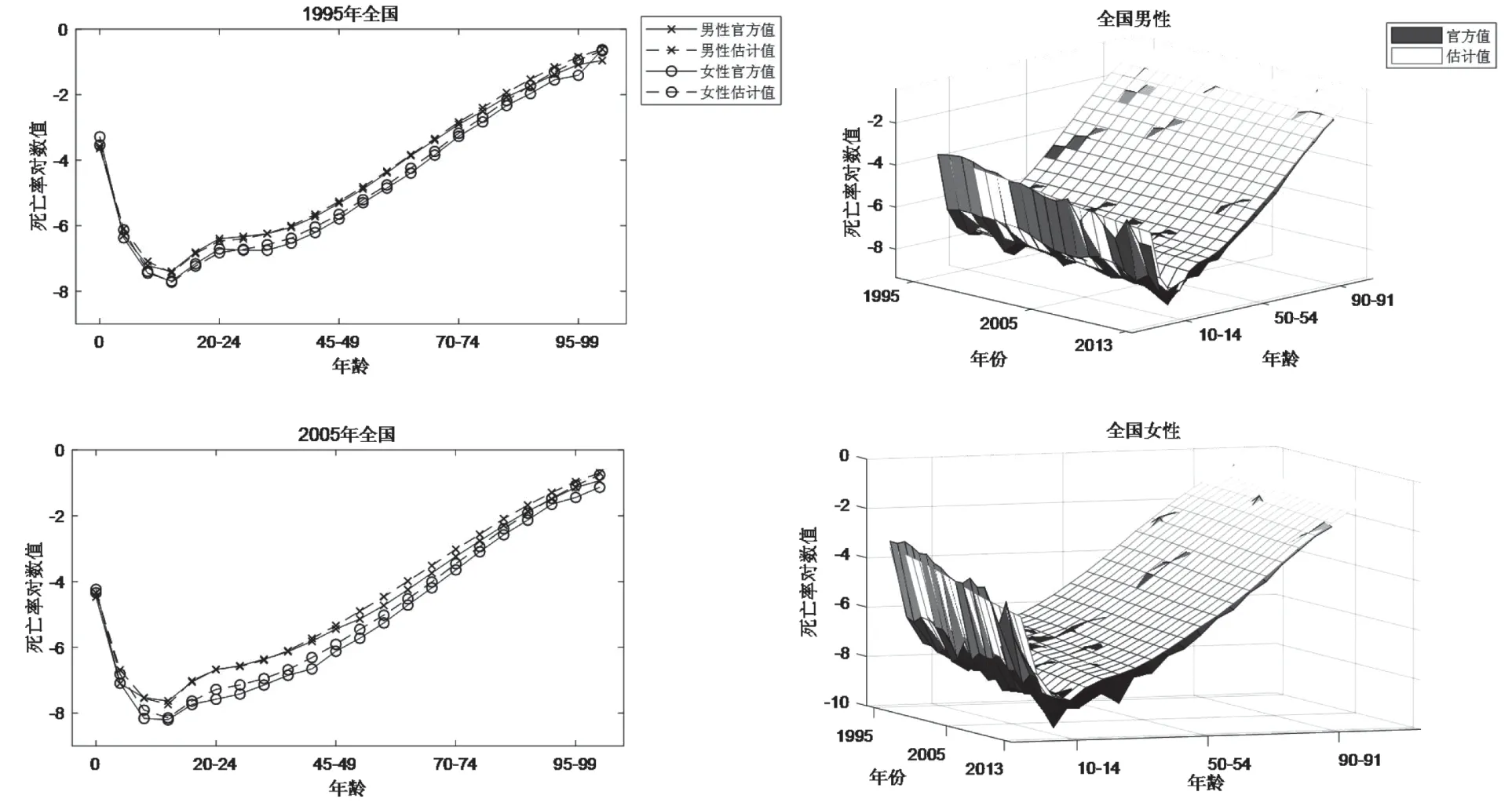
图3 1995~2013 年全国水平人口死亡率

对于85 岁以下人口死亡率，SVD-Comp 模型具有不错的拟合效果，模型值符合真实值的变化趋势（见图2），此外该方法引入我国台湾地区和日本人口的高质量死亡数据，借鉴此数据信息，可看作是对我国实际数据的修正平滑。

对于85 岁以上人口死亡率，真实值往往存在死亡率 “下陷”的情况，一个可能的原因是在我国高龄人口中存在明显的“劣淘优存”现象，长寿老人是经过“自然选择”后身体素质较高的人口，因此死亡率会降低，但这个现象在其他国家（地区）的高龄人口中并不常见，也不像我国数据如此明显，况且高龄人口的数据质量一直存在争议，利用Kannisto 模型的扩展数值保留了死亡率随年龄增长的变化趋势，更符合HMD 数据库中各国（地区）高龄死亡变动模式，模型结果与原始值的偏差也在可接受范围内。

4.2 模型插补效果分析

从《中国人口和就业统计年鉴》⑨http://data.cnki.net/yearbook/Single/N2019030259或WPP2019⑩https://population.un.org/wpp/获取全国水平的人口死亡率和预期寿命数据，同估计值进行比较，用于检验本文所用模型的数据插补能力。

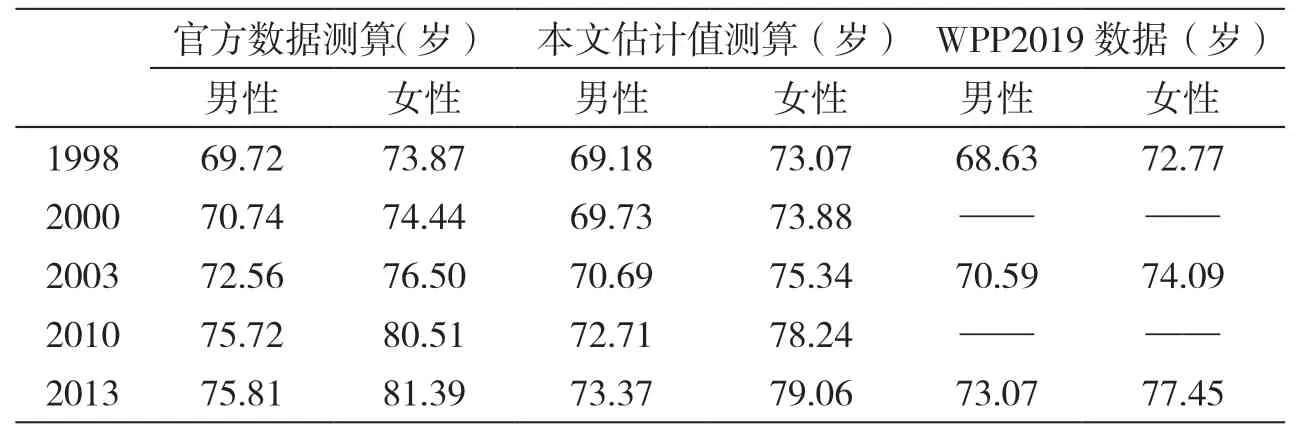
表1 全国新生儿预期寿命

全国水平死亡率数值的比较。本文估计值和官方值之间差异较小，同时官方数据包含的不规则变动较多，而估计值的变化相对平滑（见图3）。另外，模型估计值总是略高于官方值，这与各年龄段死亡人口均存在漏报的现象保持一致，模型具有一定数据修正作用。

图4 我国省域新生儿预期寿命测算结果

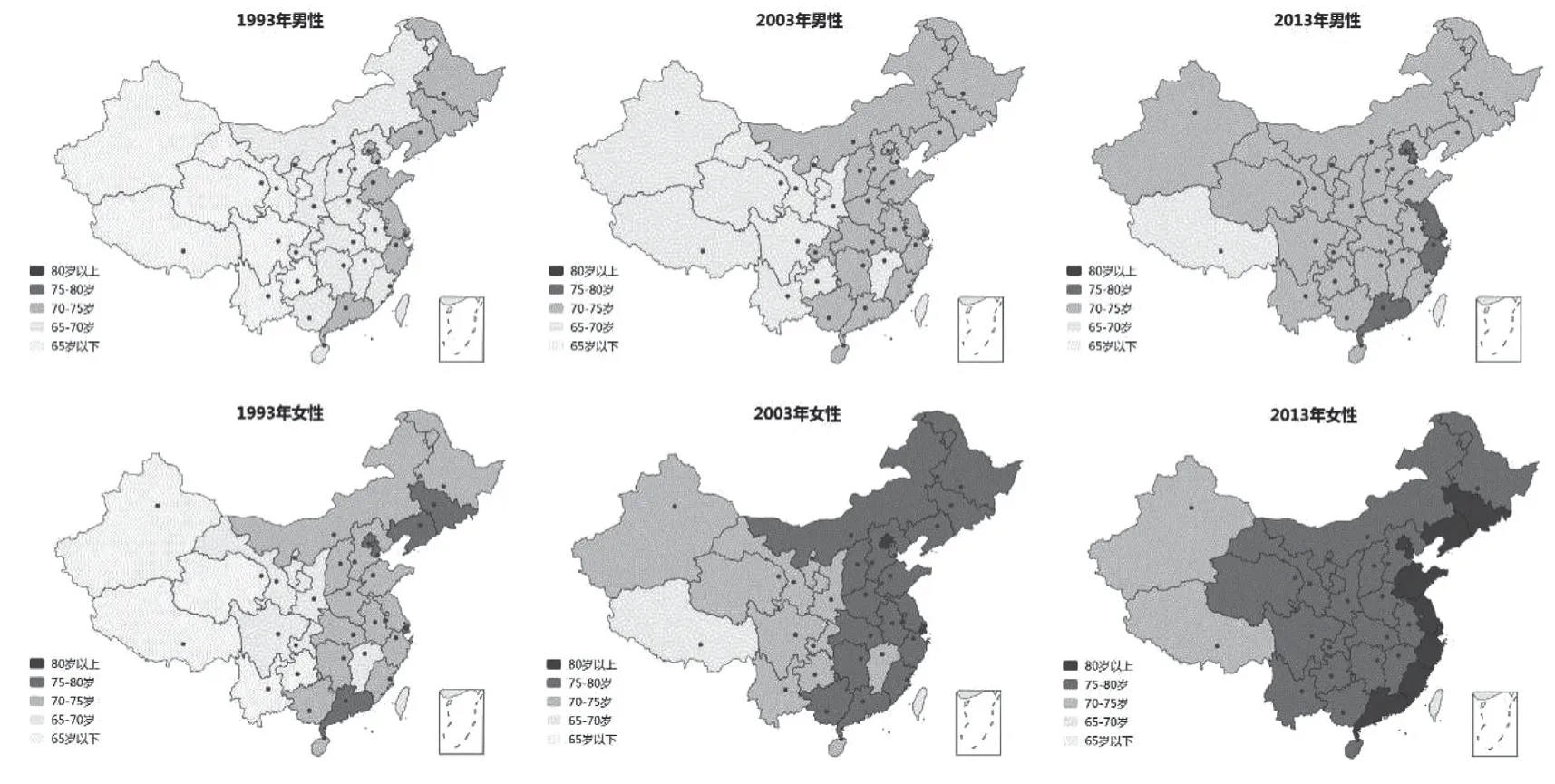
图5 1990~2013 年我国各省市分性别人口预期寿命

全国水平预期寿命的比较。依据《中国人口和就业统计年鉴》公布的与本文估计的全国水平人口死亡率（见表1），分别计算预期寿命水平，并在WPP2019 中找到对应数据 ( WPP2019 数据为五年一期，因此1998、2003 和2013 年数据分别为1995~2000 年、2000~2005 年和2010~2015 年的区间数据，同时造成WPP2019 数据在2000 年和2010 年两个普查年份缺失)，将三种来源数据进行对比。整体来看，根据官方数值测算的预期寿命水平最高，而WPP2019 的数据最低，而本文计算结果介于两者之间，说明本文所用方法比较合理，结果具有可信性。

省域水平预期寿命的比较。再从省域层面来看，将本文测算的分省新生儿预期寿命（e0），与《2018中国人口和就业统计年鉴》公布结果（表1-10）进行比较，见图4。可以看出本文测算的分省e0，在各地区排序上和官方结果基本保持一致，但本文测算结果各地区的整体波动性更小，在连续年份上的变动更加合理，关于省域e0动态变化的分析将在后面详细讨论。总之，无论从分年龄死亡率还是预期寿命的角度看，模型拟合和预测都有不错的效果。

5 我国省域人口预期寿命的动态演变

本文估计结果表明，不同年龄人口死亡率均有所改善，但改善水平却不相同，总体来看，研究期内我国婴幼儿死亡改善较为明显，而高龄人口死亡改善相对缓慢。1990~2013 年期间，以男性为例，0 岁组死亡率下降最多的前三个地区为四川、云南和贵州，分别下降了87.3%、83.7%和83.6%，其中全国水平为下降77.4%；50-54 岁组死亡率下降最多的前三个地区为西藏、四川和贵州，分别下降39.3%、38.6%和38.0%，其中全国水平为下降19.2%；而100+ 岁组下降最多的前三个地区为四川、山西和云南，分别下降22.1%、19.5%和19.4%，全国水平为下降17.5%，全年龄段整体来看，西南地区死亡改善最多。

从新生儿预期寿命水平分析，见图5 和表2，可以看出在研究期内，东部地区预期寿命要明显高于西部，女性预期寿命显著高于男性。结合图4，以本文测算结果为准，1990 年男、女性预期寿命最高的前三个地区均为北京、上海和天津，对应男性预期寿命分别为72.44 岁、72.05 岁和 71.93 岁，女性分别为77.88 岁、77.35岁和77.17 岁，全国对应水平为男性67.18 岁、女性为70.27 岁。2013 年时，男女性预期寿命前三高地区均为北京、江苏和广东，对应男性水平为77.27 岁、76.17 岁和75.85 岁，女性为82.78 岁、81.88 岁和81.60 岁，全国对应水平为男性73.37 岁、女性79.06 岁。

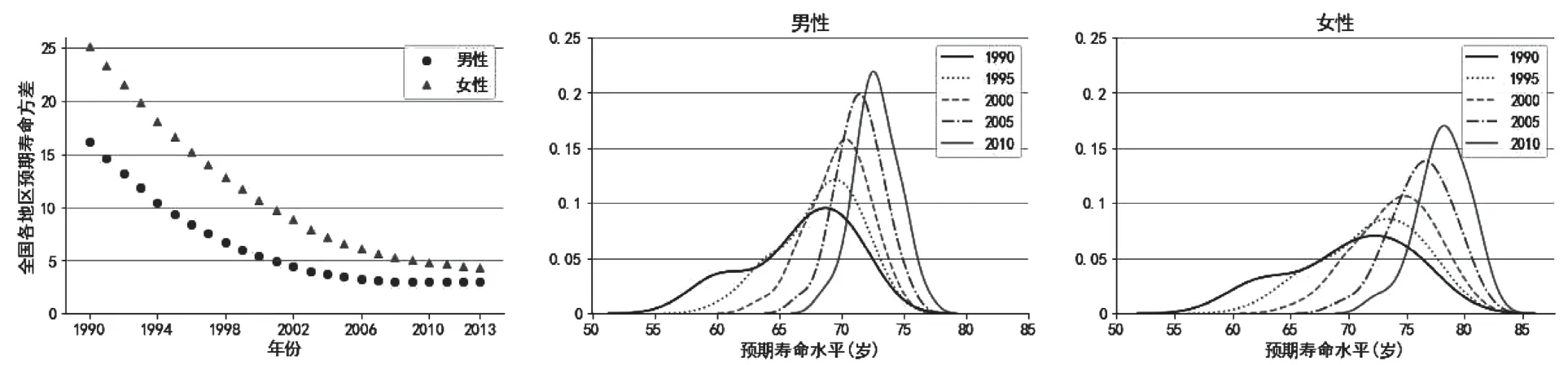
图6 我国人口死亡水平的区域差异演变

表3 1990~2013 年全国各地区人口预期寿命增速（岁/ 年）

从预期寿命提升水平看，研究期内，男性预期寿命提升最快的前三个地区分别为四川、贵州和西藏，分别提升12.3 岁、11.93 岁和11.34 岁，全国水平为提升6.19 岁；女性前三地区为四川、贵州和云南，分别提升15.77 岁、15.01 岁和14.44 岁，全国水平为8.79 岁。

总之，区域上看，东部沿海地区人口死亡率要低于西部地区，但西部地区死亡改善幅度要高于东部地区；性别上看，女性生存状况优于男性，且研究期内死亡改善状况也优于男性。

5.1 预期寿命的区域差异演变及原因分析

下面两节将对人口死亡水平的区域、性别差异演变作更详细的讨论。见图6 最左图，研究期内，我国大陆31 个省市自治区间的预期寿命差距都在减小，具体来看，1990~2003 年这一时期省域间差异缩小较快，而2003~2013 年省域差异缩小缓慢，并有趋于稳定的态势。以男性为例，1990 年时全国男性预期寿命水平第五名和倒数第五名分别是广东和四川，二者相差10.1 岁，到2003 年第五名和倒数第五名分别是广东和甘肃，二者相差4.29 岁，而2013 年时第五名和倒数第五名是天津和贵州，两者仍相差3.57 岁。由于研究期内各区域预期寿命水平均在提高，但省域间差异却在减小，这就说明预期寿命处于低水平的死亡改善较快，而位于高水平的预期寿命增长则相对缓慢。图6 中间、最右图展示了全国各地区人口预期寿命水平的分布状况，随时间发展，分布整体逐渐右移，表明全国总体预期寿命不断提升；分布的形态从较为“扁平”变为“瘦高”，表明各地区间差异不断缩小。同时，不同性别的区域差异也有不同，男性的区域差异要小于女性，这与图6 最左图的显示结果保持一致。

从预期寿命增加速度的角度，可更加清晰理解区域差异的演变过程。令g(e0(t)) 表示预期寿命增速，见公式（18），计算研究期内各省域的g(e0(t))：

将全国分为华北（京、津、冀、晋）、东北（蒙、辽、吉、黑）、华东（沪、苏、浙、皖、闽、赣、鲁）、华中（豫、鄂、湘）、华南（粤、桂、琼）、西南（川、贵、云、渝、藏）、西北（陕、甘、青、宁、新）七大地区，计算各大区每年预期寿命平均增速（见表3）。2003 年之前，各大区增速存在明显不同，西南和西北地区增速最快，华北地区最慢。2003 年之后，各大区增速都在下降，至2013 年时已有趋同态势，而一旦各地区增速相同，则在未来一段时期区域间的差异将保持稳定，该结论也与之前的分析保持一致。

5.2 预期寿命的性别差异演变及原因分析

性别间死亡水平差异的演变同样值得考究，计算研究期内各地区男女预期寿命差距，并绘制如图7 左图，可以看出，随预期寿命水平增长，不同性别间差异先缓慢增长，随后快速增长，当差异水平扩大至5.8 岁后，差异又会缩小，当在差距最大时男性预期寿命水平为75 岁，女性为80 岁。以女性预期寿命水平为准，性别间差异演变可大致划分为三个阶段：预期寿命水平63 岁以下时，男女间差异不大，不同性别的死亡改善程度相仿；在63~80 岁水平之间，性别间差异会快速扩大，此时女性死亡改善优于男性；而在80 岁以上水平，女性死亡改善要弱于男性，两者间差异又会缩小。总之，全国各地区都遵循上述规律演变，只是所处的阶段并不相同。

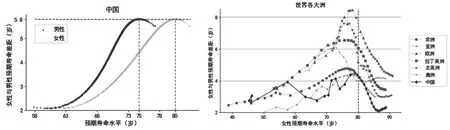
图7 我国人口死亡水平的性别差异演变

图8 预期寿命水平与其增速间的关系

本文从WPP2019 数据库整理世界各大洲和中国的不同性别人口预期寿命数据，绘制如图7 右图，从世界范围来看，性别间差距都具有先增大后减小的变化规律，只是差距最大值和对应的预期寿命水平不同。有意思的是，WPP2019 的中国数据规律性较差，但在各大洲层面的规律却又与本文得到的结论相似，同时，在中国女性预期寿命达到80 岁时，性别间差距最大，随后逐渐变小，这一点也与本文结论保持一致。

要详细了解人口死亡改善过程中区域与性别差异形成的原因，则需知道我国人口预期寿命的增长路径，将1990~2013 年我国各地区g(e0(t))随e0(t) 增长的变化绘制如图8 散点图。可以看出，不论性别，随预期寿命水平增加，其增速具有“先增加在减小后平稳”的变化规律，这说明预期寿命的改善程度在不同阶段是完全不同的，以女性预期寿命水平为例，预期寿命增速可化为三个阶段，如图8 右图，而我国地域辽阔，不同区域、不同性别人口预期寿命水平各不相同，按此变化规律增长，就会产生不同的差异变化。值得注意的是，当男性e0达到72 岁，女性达到78 岁时，e0增速，即g(e0(t))，将低于0.2 岁/ 年，此时预期寿命的增长将较为缓慢且较为稳定。

本文只对散点做平滑处理，若要量化差异，可先求出g(e0(t))的显示方程，再根据不同地区初始e0水平，结合公式（18），得到预期寿命增长路径后，就可预测预期寿命水平，完成量化区域、性别差异的目标，具体参见Raftery 等人的研究[34]。

6 总结和展望

死亡率是衡量一个国家（地区）人口整体健康状况的重要指标，能直观反映人口生活质量，也是判断社会经济、科学和文化水平的重要依据。对于我国这样一个地域广阔、民族众多，卫生资源与医疗服务等方面发展仍不均衡的国家，省域人口死亡状况必然存在差异。我国省域人口分年龄死亡率，仅可通过人口普查资料获得，数据有限且不连续，这阻碍了相关研究和分析的深层讨论。鉴于此，本文通过近三次人口普查资料，结合与我国大陆人口死亡模式相近的中国台湾和日本数据，使用SVD-Comp 模型，通过我国分省五岁以下儿童死亡数率，预测1990~2013 年我国省域分性别分年龄人口死亡率，并用Kannisto 模型对85 岁以上人口死亡率进行修正，本文得出的主要结论有：

整体来看，1990~2013 年期间我国各地区人口死亡均得到大幅改善。1990 年全国男性预期寿命67.18 岁，女性70.27 岁。2013 年全国男性预期寿命达到73.37 岁，女性为79.06 岁。研究期内人口预期寿命的增长并不均匀，1990~2003 年我国人口死亡改善幅度较大，2003 年之后则相对缓慢，原因是男性预期寿命达到72 岁、女性达到78 岁后，寿命增长幅度下滑至0.2 岁/年，且该增速趋于稳定。

年龄上，全年龄段人口死亡率均有下降，但各年龄改善状况却大不相同，其中0 岁组人口死亡率下降最快，而高龄人口（85 岁以上）死亡率改善相对较弱。区域上，研究期内各地区人口预期寿命水平差异不断缩小，其中西南地区人口寿命增长幅度最大，而在经济发达地区，如北京、上海等地增速相对较慢，全国预期寿命水平的空间特征一直为“东高西低”，随着各地区预期寿命增速逐渐趋同，未来省域间差异将会保持稳定。性别上，女性寿命要高于男性，且研究期内女性死亡改善程度也持续优于男性，各地区男女寿命差异均在拉大，且预期寿命水平越低的地区，性别间差距增长越快，但不同性别预期寿命最大差值为5.8 岁，达到此差值后，性别间差异逐渐缩小。

最后值得讨论的是，本文研究区间为1990~2013 年，但存在进一步预测未来年份数据的三个思路：首先是采用经济指标代替生命指标，本文采用5q0的数据长度即为1990~2013 年，若此数据更长，则可预测相应年份死亡率，而经济指标（如，人均国内生产总值）的统计历史更久，省域数据充裕，且经济水平也与死亡水平存在联系，故可作此尝试。其次是利用本文研究结果，由于已有连续24 年分省数据，使得利用随机死亡率模型及其变种模型进行预测成为可能[35]。最后是估计公式（18）的显示方程，求得预期寿命增长路径，再结合模型生命表方法，即可得到对应的分年龄死亡数据。