基于BREACH模型的某水库土坝溃坝分析研究
2021-05-21刘凤茹赵昱豪詹达美
刘凤茹,赵昱豪,詹达美
(1.深圳市广汇源环境水务有限公司,广东 深圳 518001;2.河海大学水利水电学院,江苏 南京 210098)
近年来,不少地区雨洪频发,给一些水库大坝带来严峻的考验。尤其是土坝,更易造成溃坝,将会产生严重的失事后果。因此,大坝溃坝问题是当前大坝安全的重要研究问题之一。大坝溃决方式主要有瞬时整体溃决、瞬时局部溃决和逐步溃决等形式[1-4],瞬时整体溃决、瞬时局部溃决是指坝体整体或局部突然倒塌或消失。而逐步溃决是指由于水流作用,不断对坝体某薄弱部位进行冲刷,形成溃口,溃口逐渐扩展,最后导致坝体破坏的溃决方式。重力坝和拱坝的溃决方式主要为瞬时整体溃决和瞬时局部溃决,而土石坝的溃决方式一般为逐步溃决。按照逐步溃决的成因来分,逐步溃决可分为漫顶溃决和管涌溃决[5-6]。
目前,大坝溃决机理研究的模型已取得一系列成果,DMBRK模型[7]、MIKE 11 DB模型[8]、BEED模型[9]、BREACH模型[10-11]都可用来对大坝溃决进行计算分析。本文采用BREACH模型对某土坝溃坝过程中的溃口流量、上下游水位和溃口宽度等参数进行分析研究。
1 溃坝分析模型与溃坝模式
1.1 BREACH溃坝分析模型
BREACH模型是由美国气象局基于土坝溃坝过程线[12]而构建的一个用于计算逐步溃决类问题的数学模型。该模型将水力学、土力学、坝体几何尺寸、坝体材料属性等融合于一体构建[13],能够描述逐步溃坝过程中泄流水位过程曲线、溃口流量过程曲线、溃口宽度变化过程曲线、累计泄水流量过程曲线等。
BREACH模型可模拟土坝的破坏,可用于均质土坝或可能含有“内外”2种材料属性相差较大的分区坝(如心墙坝)。BREACH模型也可计算滑坡、堆渣等非人工因素形成的天然堆积体的溃决。溃决方式包括漫顶失事和管涌失事。漫顶失事时,假定从局部薄弱点开始溃决,并随着水流冲刷溃口逐渐扩大,溃口底宽根据最大水力效力计算,其边坡稳定根据土力学原理计算,冲刷由泥沙输移方程计算。
BREACH模型采用水量平衡关系模拟库水位的变化,即:
(1)
式中t——时间;zs——库水位;As——库面面积;Qi——入库流量;Qb——溃口流量;Qsp——溢洪道出流量;Qsl——闸门出流量。
1.2 溃坝模式
1.2.1漫顶溃坝
漫顶导致溃坝的水流侵蚀[14-15],若大坝下游面无草覆盖,存在一条矩形溪流,溪流对坡面侵蚀的作用使坝体形成一定宽度的河渠,河渠中的水流流量用宽顶堰流量公式计算,即:
Qb=3B0(H-Hc)1.5
(2)
式中Qb——河渠中的流量;B0——初始矩形形状河渠的瞬时宽度;H——坝前水位高程;Hc——溃口底部高程。
若大坝下游表面有草覆盖,漫顶水流速率采用曼宁公式计算。若下游坡面无草被覆盖层,溪流内部的侵蚀持续发展,沿着下游坡面的水流速率计算见式(3)、(4):
q=3(H-Hc)1.5
(3)
(4)
式中q——单宽漫顶流量;H-Hc——超过堰顶部的静态水头;n′=aqb——草被均匀覆盖河渠后的曼宁系数;y——溃口河渠中水流深度;ZD——大坝下游坡比;a、b——网格曲线系数,BREACH模型建立后自动生成;v=q/y——下游坡面水流速率。
漫顶溃决,一般假设初始溃口为较小的矩形,溃口宽度计算式为:
B0=Bry
(5)
式中,Br为基于最合适河渠水力有效作用的一个因子,对于漫顶破坏,参数Br值为2,对于管涌破坏,参数Br值为1.0。
考虑陡峭河渠条件下,溃口坝料输移计算公式为:
(6)
式中Qs——坝料冲蚀率;d30、d90——含量占总重量30%、90%的颗粒粒径;P——湿周;n——曼宁系数;S——溃口河渠边坡坡比;Ω——与土体材料性质相关的阈值。
溃口处两边土体倾斜临界高度函数表达见式(7):
(7)

不同类型坝体的漫顶溃决概化见图1—3。
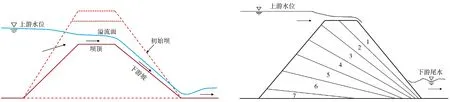
图1 非黏性土坝及松散土坝漫顶溃决概化示意

图2 黏性土坝及碾压土坝漫顶溃决概化示意
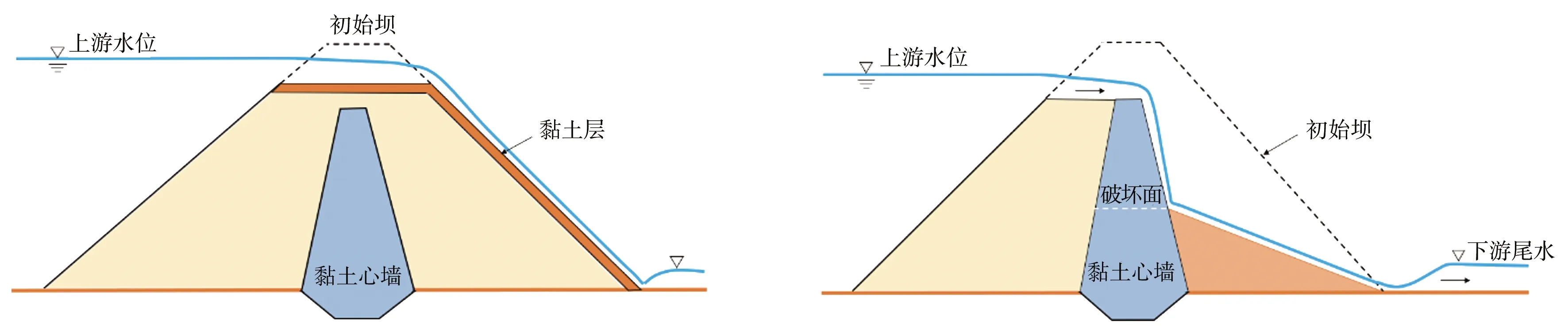
图3 黏土心墙坝漫顶溃决概化示意
由图1—3可知,非黏性土坝或松散土坝发生漫顶溃决,坝体土体由下游逐层向上游溃决(即图1坝体1区向7区逐层溃决);黏性土坝或碾压土坝发生漫顶溃决,坝体的顶部和下游表层土体发生阶梯式溃决,但相对于非黏性土坝,黏性土坝不易发生溃决。因此,黏土心墙坝发生漫顶,顶部和下游坝体的非黏性土坝体发生溃决,黏土心墙及上游的坝体不易发生溃决。
1.2.2管涌溃坝
管涌溃坝时,应保证水库水位大于坝体发生管涌后矩形河渠的中心线高程,管涌通道顶部和底部受到垂直向侵蚀[16],溃口宽度计算同式(5),通过管涌通道的流量为:
Qb=A[2g(H-Hp)/(1+fL/D)]0.5
(8)
式中Qb——通过管涌通道的流量;A——溃口横断面面积;g——重力加速度;Hp——中心线高程;H-Hp——溃口静态水头;L——管涌通道长度;D——管涌通道直径或宽度;f——摩擦因数。
水流从孔口出流控制转变成堰流控制是当管道顶部高程(Hpu)向上垂直发生侵蚀时出现这种转变关系,需要满足以下不等式:
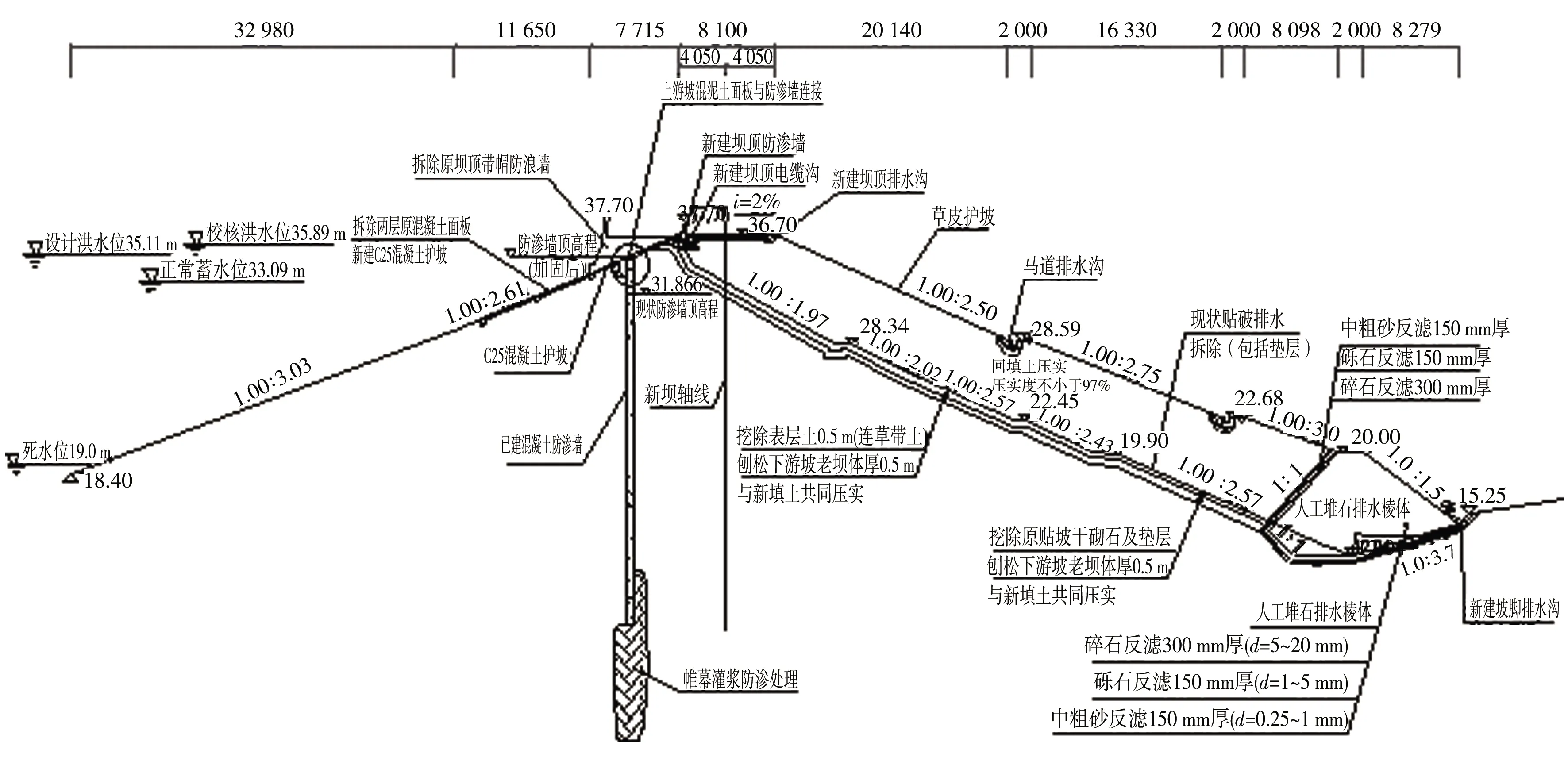
H (9) 管涌溃决概化见图4。 图4 管涌溃决概化示意 某水库建于1957年10月,1958年基本建成并投入运行。此后,水库大坝、输水涵曾多次进行除险及安全加固,其中1966—1968年对水库进行扩建,库容从1 050万m3增加至2 050万m3,同时增设溢洪道;最近一次除险加固于2013年5月竣工验收,除险加固的大坝典型断面见图5(图中大坝尺寸单位为mm)。根据2013年除险加固成果,水库总库容2 913.5万m3,属于中型水库,水库工程等别为Ⅲ等。设计防洪标准为100年一遇(P=1%),设计洪水位为35.11 m;校核防洪标准为1 000年一遇(P=0.1%),校核水位为35.89 m。 图5 大坝典型断面 水库初始水位33.086 m,入库流量为不同的水位组合,考虑洪水突发和地震突发2种事件类型,管涌溃坝和漫顶溃坝2类模式,共设置5种计算方案。其中,地震突发事件方案采用多年平均径流量0.70 m3/s。各方案设置见表1。 表1 计算方案 由现场实测资料、物理实验测得的坝体材料物理力学指标以及经验取值,溃坝分析模型计算参数见表2—5。 表2 土坝及坝下河段参数 表3 防渗墙及溢洪道参数 表4 坝体填土材料参数 表5 溃口及侵蚀参数 通过计算,可以得到溃口流量、上、下游水位、溃口过水面积、溃口宽度、水库下泄水量随时间的变化关系。考虑到一些方案计算成果的相似性,限于篇幅,本节仅给出方案1、4、5的计算结果,见图6—8(图中t=0时刻对应设计洪水过程的t=0时刻)。5个方案的溃坝分析特征数据的统计见表6。 a)溃口流量及上、下游水位 a)溃口流量及上、下游水位 a)溃口流量及上、下游水位 表6 溃坝洪水计算结果统计 根据方案1—3的计算结果和表6分析可知,管涌溃坝模式下,洪水量级越大,最大溃决流量越大、最终溃口平均宽度越大、累积下泄水量越大。这是由于洪水量级大,水量多,增大洪水对坝坡的水压力,并作用在溃口处,使得溃口宽度增大,进而使得溃口流量以及累计下泄流量增大。但是不同量级的洪水,土坝溃口发展历时均在2.5 h左右,说明洪水量级对土坝溃口发展历时影响较小。 根据方案3、4的计算结果和表6分析可知,相同洪水量级条件下,漫顶溃坝最大溃决流量达到6 739 m3/s,明显大于管涌溃坝。同样,漫顶溃坝最终溃口平均宽度达到80.10 m,亦大于管涌溃坝。但是,2种溃坝模式下的累计下泄流量相同,均为3 632 m3/s。漫顶溃坝模式下,洪水漫过坝顶下泄,土坝浸泡在水中,使得土体强度降低,溃口土体更容易被冲刷,导致最终溃口平均宽度较大,通过溃口的流量较大。由图7可以看出,漫顶溃坝的溃口流量形状更为窄瘦、变化趋势更为陡峭,主要由于2种溃坝模式溃口发展历史相同,为2.5 h,而漫顶溃坝的最大溃口流量较大(6 739 m3/s),管涌溃坝的最大溃口流量(5 834 m3/s)小导致。 地震突发条件下(方案5),水库初始水位为正常蓄水位33.086 m,入库流量过程为多年平均径流量0.70 m3/s,水库主坝地震液化使得结构失效,管涌导致溃坝,此时溢洪道无泄洪。水量较小,相比其他方案,最大溃口流量最小,为4 525 m3/s,最终溃口平均宽度也最小,为66.32 m,累积下泄水量也最小,为2 160 m3/s。可见,在5个对比计算方案中,地震方案(方案5)最为安全。 由表6可知,在水量守恒方面,水库初始水位33.086 m对应库容为2 134万m3,100年一遇、1 000年一遇、2 000年一遇洪水过程的洪量分别为894万、1 357万、1 498万m3。不同方案的累积下泄水量与初始库容及入库洪量之和一致,溃坝分析计算结果具有较好的水量守恒性,进一步验证了模型计算结果的合理性。 采用BREACH模型对某水库进行了溃坝分析,经计算分析,主要结论如下。 a)在管涌溃坝模式下,洪水量级越大,最大溃决流量越大、最终溃口平均宽度越大、累积下泄水量越大;洪水量级和溃坝模式对土坝溃口发展历时影响不大,均在2.5 h左右;相同洪水量级条件下,漫顶溃坝的最大溃决流量、最终溃口平均宽度比管涌溃坝模式较大。 b)在不同方案对比中,地震突发情况的溃坝相对安全性更大,管涌溃坝模式比漫顶溃坝模式更为安全,洪水量级小的溃坝模式更为安全。 c)不同方案的累积下泄水量与初始库容及入库洪量之和相等,表明洪水过程具有较好的水量守恒性,进一步验证了模型计算结果的合理性。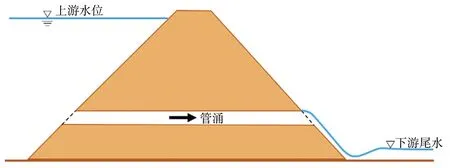
2 水库土坝溃坝实例分析
2.1 工程概况
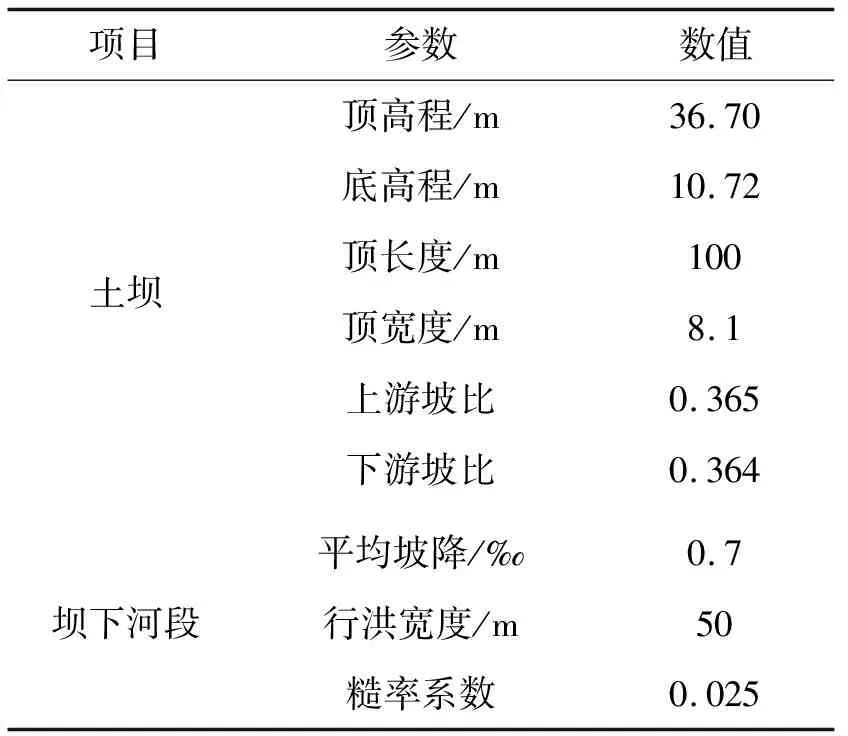
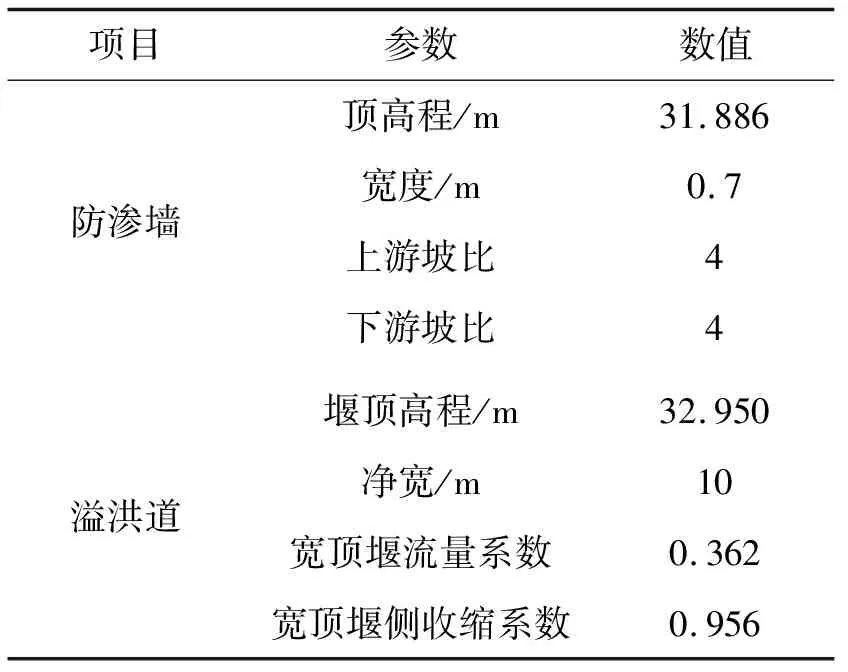
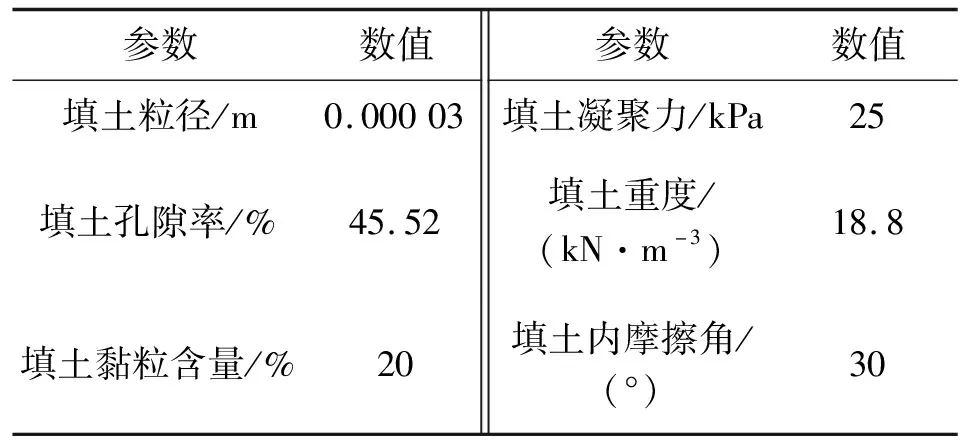
2.2 计算方案及模型参数


2.3 结果与分析
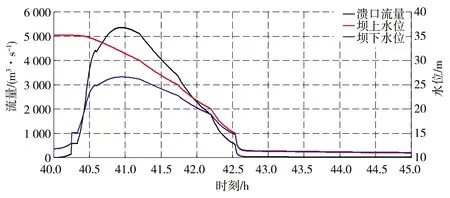

3 结论
