下穿寺庙隧道爆破振动影响的数值模拟与分析
2021-05-21刘彦涛
刘彦涛
(1.中国铁建大桥工程局集团有限公司,天津 300300;2.陕西省岩土与地下空间工程重点实验室,西安建筑科技大学,陕西 西安 710055)
钻爆法施工具有操作简单、适应性强和施工成本低等特性,是目前隧道和地下工程建设的主要方法[1].然而,在邻近建(构)筑物隧道采用钻爆法施工时,可能会对建(构)筑物产生不利影响,造成建(构)筑物结构破裂或倒塌[2].因此,通过研究隧道爆破应力波的传播规律,并推断拟定爆破设计方案执行过程对邻近建(构)筑物的影响,及时有针对性的修正爆破设计,对保证下穿段隧道施工安全和效率具有重要现实意义[3].国内外专家学者已对此课题进行了深入研究并取得较大进展.卢文波等[4,5]根据圣维南原理及应力波衰减特点,提出了在同段位多个炮孔同时起爆条件下的隧道爆破荷载的等效有限元模拟方法;宋战平等[6]根据应力弹性波静力等效的原则,提出了考虑微差效应影响的爆破振动等效荷载确定方法;陈庆等[7]结合实际工程及爆破设计参数取值特点,提出了隧道爆破应力波的衰减公式,并在邻近既有建筑隧道爆破控制设计中取得了良好的效果;高文学[8]研究了浅埋隧道的爆破振动影响因素,得出隧道的几何尺寸、隧道埋深和围岩条件以及隧道开挖方式等对其有重大影响,而掏槽眼爆破则是爆破振动影响控制的关键;王明年等[9]基于对爆破振动质点峰值振速和岩体爆破损伤的定量分析,给出了依托工程地下厂房爆破开挖时工程高边墙围岩的损伤范围;Fakhimi A等[10]通过研究气体和炮孔的相互作用提出了一种岩石爆破模拟的数值模型.
鉴于新大力寺段隧道下穿既有建筑物爆破施工特点,本文首先根据萨道夫经验公式对下穿段地震波衰减规律进行回归分析,指导下穿段单段药量及控制爆破方案的设计.其次,通过数值模拟方法对拟定方案振动控制效果进行模拟分析,确定下穿段方案的合理性及适用性.最后,由现场振动监测和数值模拟结果的对比分析,验证实施方案的控制爆破效果及数值模拟方案振速预测评价的可行性,为同类爆破控制段爆破方案设计提供参考.
1 依托工程概况
1.1 工程概况
新建商合杭高速铁路是连接商丘、合肥与杭州的高速铁路.其控制性工程新大力寺隧道全长3 354 m,最大埋深约236 m,位于巢湖市经济开发区[11],隧道路线如图1所示.新大力寺隧道与合福铁路并行通过,位于合福铁路左侧(东北侧),线间距65~105 m不等。其中下穿大力寺段(DK448+440~DK448+510)围岩等级为Ⅳ级,采用三台阶法钻爆施工,上台阶每循环进尺为1.2 m.

图1 新大力寺隧道路线图
1.2 下穿寺庙段爆破方案设计
为减小新大力寺隧道爆破施工对大力寺及运营合福铁路影响,下穿寺庙段爆破参数需结合《爆破安全规程》对古建筑及运营线的振动安全控制阈值进行设计,所设立建(构)筑物安全质点振速为2.0 cm/s[12].由现场振动监测数据指导该段初始爆破设计方案的制定,设计过程如下.
(1)单段最大爆破装药量确定
根据实测信号结合萨道夫斯基经验公式反映施工现场爆破应力波衰减规律[13,14],科学指导隧道近距离下穿建筑物的爆破施工,为爆破设计方案最大段药量和掏槽方式的选取提供依据,公式如下.
V=K(Q1/3/R)a
(1)
式中:V是质点振动速度,cm/s;Q是最大段装药量,kg;R是爆心距,m;K和α分别为与现场地质条件有关的系数.
运用Matlab软件对式(1)进行回归分析[15],回归曲线如图2所示.根据回归分析结果,由萨氏经验公式变换可得爆破振动安全允许装药量公式为

图2 爆破数据最小二乘法回归曲线图
Q=R3(V/250)3/2
(2)
由以上分析最终确定上中下三台阶对应最大段药量.上台阶最大段药量为2.88 kg,主要用于掏槽爆破增加岩体的碎涨空间,提高掘进爆破扩槽效果.中、下台阶因存在上台阶掏槽爆破后提供的临空面,其最大段药量主要设置于底眼,达到翻渣的目的,设计药量分别为11.03 kg和19.9 kg.以上数据经地震波衰减公式检验,所得结果满足隧道施工要求,符合下穿古建筑物的振速标准.
(2)钻孔和装药量设计
为了保证隧道既有古建筑物所受振动影响在安全范围之内,本工程采用了高精度多段位雷管,并结合周边建筑物特点严格控制最大段装药量.在掏槽形式上采用楔形掏槽,在拱处设置减震孔,增强地震波能量的耗散,降低地震效应对周边古建筑及运营线的影响.在周边孔的布置中采用间隔装药的布置形式,减少周边孔爆破对围岩的损伤程度.上台阶炮孔布置示意图如图3所示,上断面I和II分区爆破开挖参数表,分别见表1和表2.

图3 上台阶Ⅰ、Ⅱ分区炮孔布置图

表1 上断面Ⅰ分区的爆破参数表
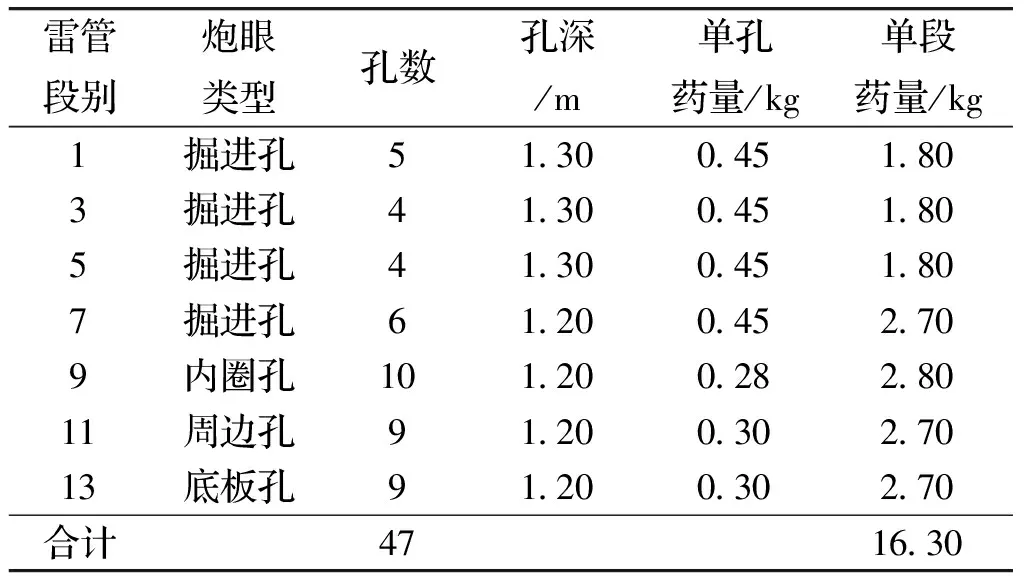
表2 上断面Ⅱ分区的爆破参数表
2 爆破施工影响分析
2.1 分析模型及模型参数
为减少试爆次数,保证爆破设计方案的振动危害控制效果,采用数值模拟方法对新大力寺隧道DK448+440~DK448+510爆破控制段爆破设计方案进行爆破振动效果分析.所建模型根据大力寺段实际工况做适当简化,地质模型简化为120 m×70 m×71.5 m地质体,地表与隧道拱顶间的距离取31.7 m.模型土层简化为地表、强风化灰岩、弱风化灰岩三层,如表3所示.有限元数值模拟模型和隧道断面尺寸,如图4和5所示.

图4 爆破振动影响数值模型
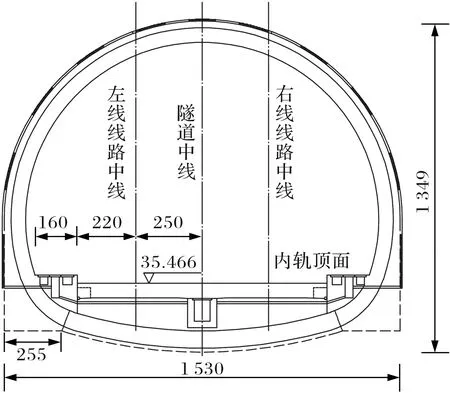
图5 新大力寺隧道的断面示意图

表3 数值计算模型参数表
2.2 爆破荷载的计算
目前对隧道爆破模拟,普遍为针对某一段位进行模拟分析,与当前隧道常采用微差爆破技术进行爆破不符[16-17].因此,传统模拟分析方法未能考虑微差延时的减震效应,使得模拟结果偏大.为更好的模拟现场爆破地震效应的影响,采用文献[6]中考虑微差效应的“群孔荷载模型”来反映爆破振动效应.其中各炮孔起爆应力的相互影响,可根据力等效原理将应力波按一定比例均布于弹性边界,此时隧道轮廓线的等效弹性边界上考虑叠加效应掏槽孔的等效时程爆破荷载为
(3)
式中:n为群孔起爆时该段位掏槽孔总数;r为破碎区半径;掏槽段荷载等效时,l为等效弹性边界周长.
由于非掏槽孔是在掏槽孔爆破后再次爆破,所以具有临空面[18],因此,本段也选用三角形荷载曲线来模拟非掏槽孔段的爆破荷载,得到在等效弹性边界的时程荷载,为
(4)
式中:n是计算区域段位起爆时的炮孔数量;r是炮孔的破碎区的半径;l是计算段位的炮孔中心连线总长.
升压和作用时间的计算采用文献[6]中经验公式,爆破荷载的升压时间为
(5)
爆破荷载的作用时间为
(6)
式中:R是距炮孔中心的距离;rb是爆破炮孔的半径(r=R/rb);μ是隧道围岩的泊松比;K是岩石体积压缩模量;Q是爆破时对应段位上炮孔的装药量.
式(6)减去(5)即为卸荷时间。结合设计爆破参数确定Ⅰ和Ⅱ分区爆破等效荷载及作用时间如表4所示.

表4 上断面Ⅰ和Ⅱ分区的爆破等效荷载和作用时间
2.3 爆破振动影响模拟结果及分析
本次计算模型采用线性时程的求解类型,即对模型结构物进行微分方程的逐步求解,通过分析,取分析时长T=2.20 s,即为作用总时间与传播时间之和,输出结果间隔0.001 s,因此会产生时程步骤计算结果2 200个.超过2.2 s后,爆破地震效应对建筑物的影响可以忽略.因建筑物监测点距爆心距离较小,爆破过程受地震效应影响较大,模拟分析应重点讨论模拟周边建筑物最危险点的影响,为爆破设计优化提供参考.
(1)隧道爆破对周围岩体位移情况
由图6和图7各分区位移累计量云图可知,Ⅰ分区爆破过程自由面较少,掏槽需克服夹制阻力较大,而Ⅱ分区爆破时已存在Ⅰ分区制造自由面,所需最大段药量相对I分区有所减少,累计位移量Ⅱ分区也相对减小.且I分区最大位移主要集中在隧道中线处,最大累计位移量为1.96 cm,Ⅱ分区最大位移主要集中在中台阶上边缘处,最大累计位移量为1.38 cm.
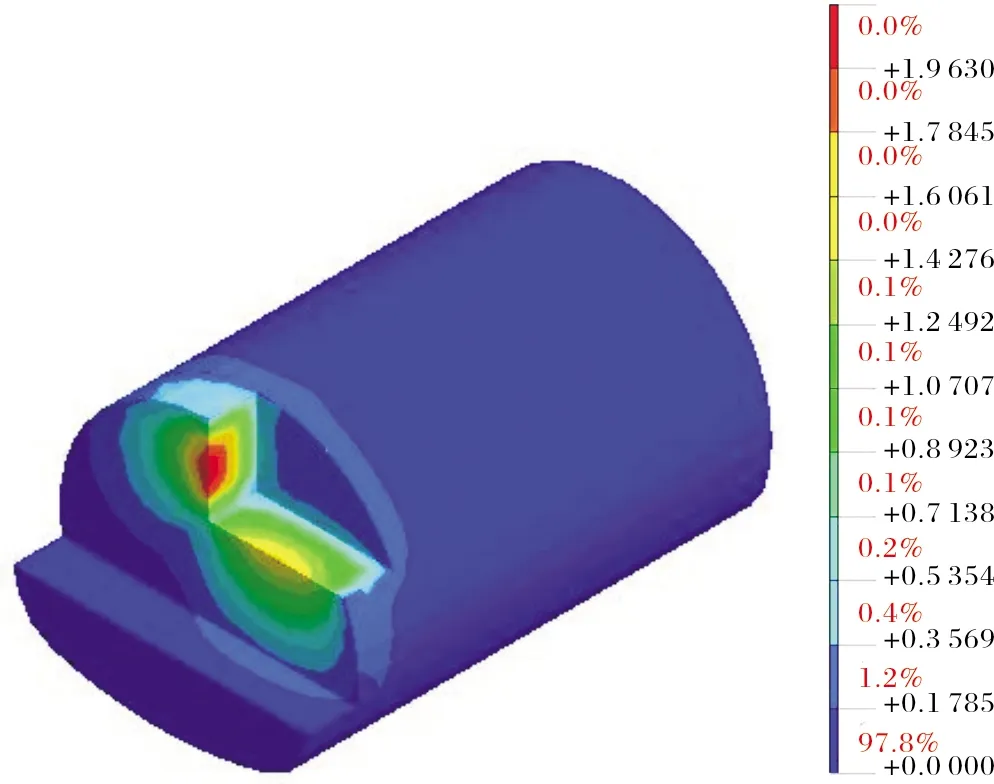
图6 上断面分区Ⅰ爆破时的位移云图(单位:cm)

图7 上断面分区Ⅱ爆破时的位移云图(单位:cm)
(2)隧道爆破对既有建筑影响的分析
由Ⅰ分区爆破测点水平和竖向速度时程曲线可知(见图8),Ⅰ分区第1段掏槽爆破引发振速峰值大于其他段位,主要是由于掏槽爆破较其他段位无更多补偿空间,不利于岩石破碎,产生地震效应较其他段位更为明显;爆破等效荷载作用引起的测点水平振速和随时间的衰减程度均小于竖直方向,但水平方向的振动持续的时间大于竖直方向.
由图8和9对两个分区速度时程曲线进行对比分析,可以发现Ⅱ分区相对于Ⅰ分区的水平向振速与竖直向振速均有所减少,水平速度峰值与竖向速度峰值分别减小了6%和21%.这是因为Ⅱ分区隧道爆破具有Ⅰ分区所提供碎涨空间,提高了应力波的反射拉伸作用和破岩效率,进而使得二者的爆破荷载产生差异,Ⅱ分区相对于I分区爆破荷载有所减少.
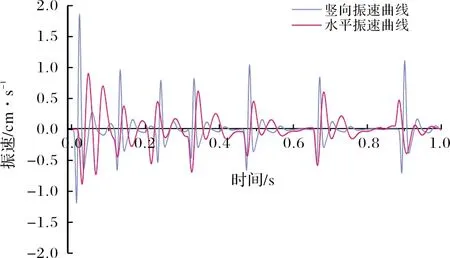
图8 上断面分区Ⅰ爆破时测点的速度时程曲线(单位:cm/s)

图9 上断面分区Ⅱ爆破时测点的速度时程曲线(单位:cm/s)
通过以上分析可知,拟定爆破方案对邻近古建筑的振动影响较小,在规范要求安全界限以内。Ⅰ分区爆破开挖时,掏槽部分需克服围岩的夹制阻力所造成的地震效应较大,但模拟测点振速峰值(1.86 cm/s)小于安全界限值(2.0 cm/s).相对于Ⅰ分区爆破开挖,Ⅱ分区的爆破所引起的振速更小,其中最大振速减小幅度更为明显。因此,结合爆破控制区周边建筑物布置特点及数值模拟结果,拟定设计方案可以满足既有建筑物的振速控制要求.
3 现场测试
3.1 监测方案
在下穿既有建筑物隧道爆破施工过程中,爆破监测可对下循环爆破方案设计提供重要指导.通过爆破监测能有效减小或避免地震效应对既有建筑物的影响,保证爆破控制段施工安全.因此,采用中科院成都研究所研发的TC-4850增强型爆破测振仪.该测振仪有三个通道,可以同时采集3个不同方向的振速、频率和持续时间.爆破振动监测点布置见图10.
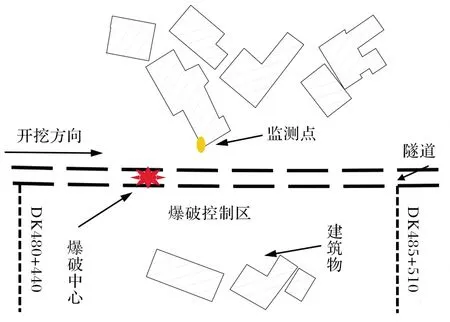
图10 爆破振动监测点布置图
3.2 模拟及监测结果分析
为验证下穿隧道爆破振动数值模拟的准确性,对爆破控制段建筑物监测和模拟测点的竖向速度时程曲线进行提取,并进行对比分析,见图11.
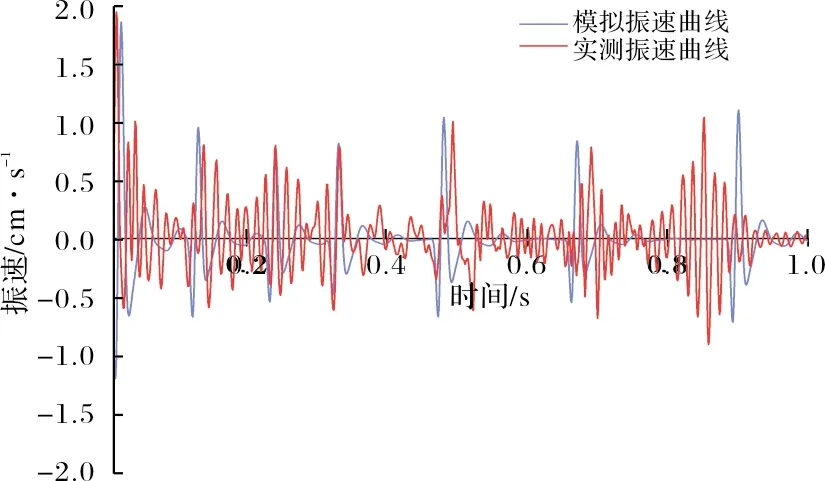
图11 Ⅰ分区模拟与实测竖向振速对比分析
通过对比分析可以看出,实测和模拟测点振速峰值及衰减规律具有很好的一致性.考虑工程地质的复杂性和数值模拟理想化等因素,两者在允许范围内存在一定的偏差是合理的.此外,由于数值模拟中忽略了岩体不均匀性和节理断层等的影响,而实际隧道围岩内存在节理裂隙及软弱夹层,导致应力波在传播过程中出现反射和折射现象,抵消和损失部分能量,使得模拟振动持时大于实际持时.采用爆破设计方案所引起测点振速峰值为1.95 cm/s满足规范设定安全振速控制要求;由Ⅰ、Ⅱ分区的水平和竖向速度时程曲线可知,竖向振速峰值最大,水平振速峰值相对较小,与现有研究对地震波传播规律相符.
4 结论
通过对新大力寺隧道下穿既有寺庙段爆破控制段监测和模拟分析,得出以下结论:
(1)根据现场实测数据进行回归分析所得系数更加符合施工段地震波衰减规律,能够有效的指导爆破方案最大段药量的设计;基于监测数据的反分析,实时优化爆破设计方案,科学指导隧道邻近既有建(构)筑物隧道的爆破施工.
(2)由新大力寺隧道下穿寺庙爆破振动影响数值模拟结果和监测结果分析可知,选定新大力寺隧道分区爆破方案,邻近寺庙监测点峰值振动速度1.95 cm/s,满足规范要求振动速度允许值;邻近建筑物隧道爆破引起的既有建筑物地震效应主要取决于掏槽爆破,掏槽方式的选择及掏槽段药量的设置是控制爆破的关键;通过数值方法对拟定方案进行分析,能够保证下穿既有建筑隧道施工更为高效和安全.
(3)在数值模拟隧道爆破开挖中,需考虑微差爆破对结果造成的影响.采用爆破荷载等效方法模拟结果表明,考虑微差效应的等效荷载引起的振动时程曲线与实测振动变化规律相一致,曲线的波峰、波谷出现的数量、时间与实测情况基本一致,对爆破设计优化具有重要指导意义.
