一种月球表面飞跃转移轨迹设计方法
2021-05-21王浩帆张洪华王泽国关轶峰
王浩帆,张洪华,王泽国,关轶峰
北京控制工程研究所,北京 100190
20世纪70年代以来,巡视器一直是行星表面无人探测的主要工具[1]。然而,这种探测方式存在固有的缺点:着陆作业时,需要一个着陆器将巡视器部署到行星表面。这既增加了任务飞行器的总质量,也增加了到达地面后巡视器与着陆器分离的复杂性。从功能的角度来看,传统的巡视器可以探测的地形类型是有限的,适合在相对平坦的地面上活动,但却不能爬上陡峭的悬崖,不能越过裂缝,也不能从地面的危险中逃生。如果目标是探索更危险、更多样的行星、卫星和小行星,目前的巡视器技术可能会限制实现任务的能力。
飞跃器是一种在星体表面上跳跃飞行的交通工具,与现有的巡视器相比具有显著的优势[2]。飞跃器可以快速移动至待探测区域,并能克服地形障碍,如巨石和火山口。因此,飞跃器作为一种可以为行星探索提供重要用途的技术,在未来具有重大的发展潜力。2007年,南加州大学的信息科学研究所和航天与空间技术部门开发了月球进入与接近的地面研究平台(lunar entry and approach platform for research on ground, LEAPFROG),将其作为月球着陆技术的开发和测试相关挑战的解决方案[3]。2009年,为了发展一种可以在月球表面着陆,穿越指定距离,并将数据发回地球的飞行器,谷歌举办了X-Prize竞赛。麻省理工学院的下一个巨大飞跃团队(next giant leap, NGL)将飞跃器作为主要研究项目,并开发了陆地人造月球与简化重力模拟器(terrestrial artificial lunar and reduced gravity simulator, TALARIS)试验台[4],用来研究飞跃器的制导、导航与控制算法。文献[5]中设计了一种新型高原地形飞跃器(highland terrain hopper, HOPTER),该飞跃器结构简单,机动性强,成本低廉,可以编队组网飞行对复杂地形进行探测。文献[6]中设计了一种基于气囊的飞跃器,具有鲁棒性好、成本低等优势。
标准轨迹设计是实施制导和控制的重要指标,要求能够预定着陆场景,同时满足多种约束条件,从而提高任务的安全性和可靠性。从产生标准轨迹的计算复杂性和实时应用考虑,将标准轨迹生成可以划分为离线轨迹优化和在线轨迹优化两种。采用离线生成轨迹作为标准轨迹,是在任务之前进行计算,然后将数据存储到星载计算机上,对计算成本要求较低,更多是考虑如何在多约束的复杂条件下寻找到最优解。离线轨迹优化的本质是解决复杂约束下的最优控制问题。间接法和直接法是最常用的两类方法[7]。间接法是利用极大值原理将最优控制问题转化成两点或者多点边值问题,需要引入协态变量,但是协态变量没有明确的物理意义,算法对协态变量的初值猜测很敏感。直接法是将变量参数化,将连续动力学方程转化为一系列代数方程,原最优控制问题就变成了非线性规划问题,然后通过已有的数值算法求得最优轨迹。直接法相对间接法应用更为广泛,而且有很多不同类型的直接法。伪谱法是一种求解非线性规划问题很有效的直接法[8],通过使用非均匀网格,以及计算可行解时需要的较少的节点,从而得到更平滑的解。文献[9]针对临近空间滑翔式高超声速的特点,采用高斯伪谱法对固定翼飞行器和折叠翼飞行器进行了轨迹优化,提出了一种综合目标与约束的轨迹优化思想。但是伪谱法由于需要对控制变量参数化, 无法保证全局最优性,而且计算成本高,应用受到了一定的限制[10]。近年来,全局智能优化算法的发展为解决轨迹优化问题提供了一种新的直接方法。文献[11]针对升力式火星探测器进入火星大气段,采用遗传算法对进入轨道进行优化设计,提出不同的推力发动机制动方案。文献[12]提出一种基于随机森林的模型对月球着陆过程轨迹重规划技术,利用离线训练好的模型根据航天器状态在线计算其控制量,降低了航天器位置速度误差。但是,由于智能方法目前仍缺乏完善的理论证明,可靠性较低,限制了其实际应用。
另一种近年来发展迅速的直接法是凸优化方法,对于一个优化问题而言,得到全局最优解的条件取决于系统的凸性而不是线性,极大扩展了使用优化方法求解的问题[13]。在此条件下,问题可以实时解决,而且如果问题是可行的,计算出的解就是全局最优解。文献[14]中将火星动力下降问题转化为求解二阶锥问题(second order cone problem, SOCP),通过内点法使问题在多项式时间内得到求解,从而使在线轨迹优化成为可能。随后采用凸优化方法求解飞行器最优轨迹的研究逐渐增多。文献[15]中提出了一种连续凸化技术,解决了动力下降段中存在气动阻力和非凸约束的问题。文献[16]中考虑了导航及障碍检测敏感器视场约束及制动发动机推力大小,研究了凸优化方法处理含有复杂约束的着陆轨迹优化问题。文献[17]针对传统内点法求解效率不高的问题,提出了一种机载使用的实时算法。文献[18]中,美国国家航空航天局(national aeronautics and space administration, NASA)基于凸优化理论开发了大转向燃料最优制导(guidance for fuel-optimal large diverts, G-FOLD)软件,并在Xombie火箭上验证了其有效性。文献[19]中考虑了小天体的不规则地形和弱引力场,提出了一种基于凸优化方法的小天体飞跃的制导算法,将飞跃器在初始段和着陆段受到的约束均考虑为二阶锥约束,具有较高的鲁棒性和精度。这些方法可以适用于飞跃器单个阶段的最优燃料轨迹规划,但不能解决全任务阶段的轨迹规划问题。这是由于这些研究都是在整个运动过程中约束相同的条件下进行的,而在实际工程中,飞跃器在起飞时受发动机指向限制且不能与周围环境相撞,因此需要垂直上升。上升到一定高度后发动机转向开始飞跃。到达目标点时,为了保证飞跃器安全稳定地着陆,加入了垂直下降约束。这三个阶段受到不同的高度和推力约束,因此需要对凸优化方法进行扩展。
本文针对飞跃器转移过程中存在垂直起飞、飞跃、垂直下降阶段约束不同的问题,从凸优化求解算法出发,通过假设上升和着陆时间相同,简化了分析模型,然后利用黄金分割法搜索最优燃耗对应的上升、着陆时间以及飞跃全程的时间,在整个凸优化框架内对不同的阶段采用不同的推力和位置约束,采用内点法得到了最优燃耗解,并通过两个仿真算例校验了算法的合理性和有效性。
1 飞跃过程建模
飞跃过程是指飞跃器从起始点以静止状态垂直起飞,利用变推力发动机到达目标点上方,然后垂直着陆至目标点。
1.1 坐标系建立
忽略月球表面曲率影响,建立如图1所示的月球表面飞跃坐标系O-XYZ,原点O为目标着陆点,OX轴指向从着陆点到月球质心的反方向,OY轴指向初始飞跃点,OZ轴由右手法则确定。
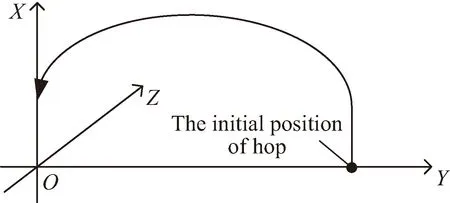
图1 飞跃坐标系Fig.1 Hop trajectory frame
1.2 动力学方程建模
行星飞跃主要有两种方式——巡航式和弹道式,飞跃方式如图2所示。由于受到姿态要求和推力指向要求,弹道式飞跃在飞跃器上升到一定高度后,增加推力进行弹道式飞跃,达到一定的高度和速度后减小发动机推力或关闭发动机。当飞跃器即将接近目标时进行减速制动,飞跃器到达目标上空一定高度时下降,实现定点软着陆。通常还需要满足半矩形约束,即除了上升段和着陆段外,飞行轨迹不能与虚线相交。这种方式只需要发动机在发射段和着陆段提供推力,可以节省燃料。
巡航式飞跃是指飞跃器先上升到一定高度,然后水平向目标移动,运动过程中,垂直方向上必须始终由发动机施加与月球重力加速度相等的控制加速度,水平方向上采用先加速,然后滑行,最后减速的方式接近目标点。由于发动机在整个飞行过程中都是开机状态,因此预计飞行燃耗会更高[20]。
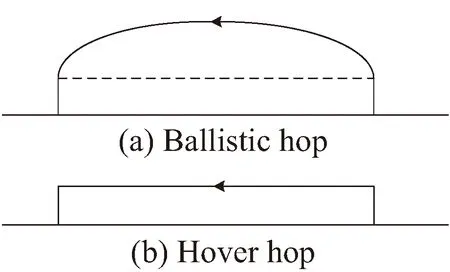
图2 两种类型的飞跃轨迹Fig.2 Two types of hop trajectories
不考虑月球自转的影响,并且将月球加速度视为常量处理,飞跃器的动力学方程为:
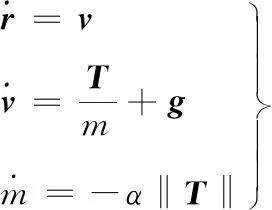
(1)
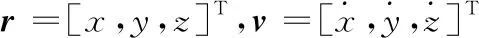
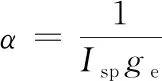
(2)
式中:Isp为发动机比冲;ge为地球表面加速度大小。
1.3 优化问题建模
对于深空探测任务,燃耗是重要的性能指标,节约燃料越多,越有利于有效载荷的增加和成本的节约。同时,燃耗少也能节省整个飞行器的质量,更加有效地进行探测任务,因此把燃料消耗最少即燃料最优作为着陆轨迹优化目标的研究可以为着陆之后的探测任务提供更好的基础。
以燃料最优为目标的模型可以描述如下:
(1)性能指标
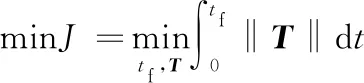
(3)
式中:tf表示到达目标点的时间;J为燃料最优的性能指标。
(2)约束条件
对于弹道式飞跃器来说,首先由月面飞行到一定高度,然后进行弹道式飞跃,飞跃至目标点上方一定距离后,缓慢到达预定着陆点,状态约束条件如下:
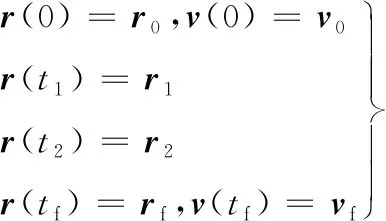
(4)
式中:r0,r1,r2,rf,v0和vf∈R3为常值。
此外,因为初始上升段和末端着陆段要求是垂直上升和下降的,因此这两个阶段的推力方向约束为:
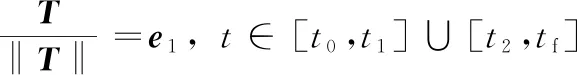
(5)
式中:e1=[1,0,0]T表示OX方向的单位列向量。
考虑一定的工程实际,由于推进系统的能力有限,飞跃器的控制推力幅值约束为:
0≤Tmin≤‖T‖≤Tmax
(6)
式中:Tmin和Tmax分别为推进系统的最小推力幅值和最大推力幅值。
飞跃过程中,为了保证飞跃器不与障碍碰撞,需要加入高度约束,即:
rx(t)≥hd,t∈[t1,t2]
(7)
式中:rx为r在OX方向的分量;hd为根据任务轨迹附近月球表面的起伏程度所确定的高度。
2 飞跃转移过程的凸优化方法
2.1 控制约束的凸化处理
由以上分析,燃料最优飞跃模型是求在满足式(4)到式(7)的约束条件和式(1)的运动方程下使得式(3)的性能指标最小的最优控制变量和最优状态变量。由于式(6)描述的约束条件中含有幅值下界从而成为一个非凸约束问题,直接求解可能会陷入局部最优,所以需要将非凸约束问题进行一定的转化后再求解。由文献[14]可知,可以通过引入松弛变量Γ而将式(6)转化为如下的凸约束:
推力方向约束为
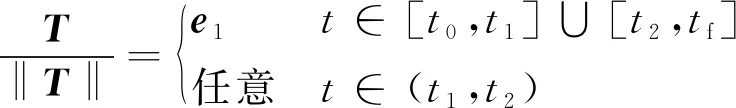
(8)
约束(8)导致无法利用传统的凸优化算法进行计算,因为在飞跃的过程中,不同阶段约束不同,对于这种情况,可以采取两种处理方式——分段凸优化和全程凸优化。分段凸优化指将飞跃过程分为上升段、飞跃段、下降段,每个阶段分别进行计算,但是这种方式需要给定上升段和飞跃段末端速度约束,否则无法得到全局最优解。而如果采用全程凸优化,一个关键的难点是无法确定推力约束的切换时间点。因此,本文考虑采用线搜索的方法得到推力切换点。
2.2 推力切换点的计算
对于一般工程情况,上升段和下降段的时间远小于飞跃时间,不妨先假设上升段和下降段的时间相同,通过下述方法来确定飞行时间的上界和下界。
考虑如果用最短的时间上升,即采用最大推力上升,所需时间为:
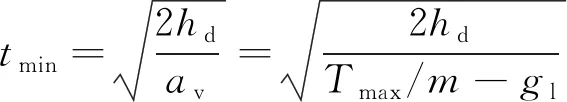
(9)
式中:av为飞跃器的垂向加速度大小;gl的定义见式(1);hd的定义见式(7)。式(9)在计算过程中未考虑质量变化,由于采用最大推力时,飞跃器质量变化较大,因此实际上升时间更少。
对于时间上界的计算,如果按照最小推力计算,即:
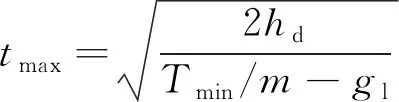
(10)
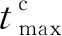
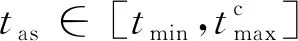
(11)
2.3 变量等效与离散化
为了方便采用数值算法来求解,考虑如下的变量等效:
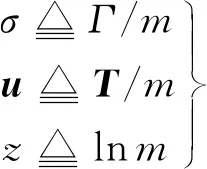
(12)
式中:σ为松弛变量的等效变量;u为等效推力矢量;z为等效质量。
将式(12)代入式(1),则动力学方程式(1)的第二、三个等式变为:
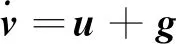
(13)

(14)
从式(14)可以推出:
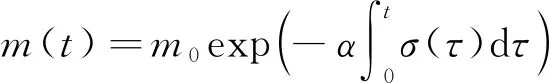
(15)
式中:m0是飞跃器的初始质量。
因为α>0,则燃耗最小性能指标函数等价于:

(16)
用等效变量表示的控制约束如下:
‖u(t)‖≤σ(t),∀t∈[0,tf]
(17)
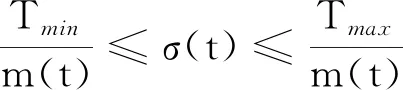
(18)
将式(12)代入式(14)和(18)得:
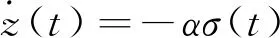
(19)
Tmine-z(t)≤σ(t)≤Tmaxe-z(t),∀t∈[0,tf]
(20)
不等式(20)的第一部分定义了可行解的凸区域,但是第二部分不是。因此考虑采用二阶锥和线性近似来处理这些不等式约束。将第一部分用二阶锥来近似(通过用e-z(t)泰勒展开的前三项来近似):
Tmine-z0(t){1-[z(t)-z0(t)]+
式中:z0(t)=ln(m0-αTmaxt)。
式(20)的第二部分用线性近似(通过用e-z(t)泰勒展开的前两项来近似):
σ(t)≤Tmaxe-z0(t){1-[z(t)-z0(t)]}
(21)
从而得到式(20)的二阶锥和线性近似:
将整个着陆过程的时间[0,tf]均匀分为N-1段,每段间隔为Δt,则对应的时间节点为
tk=kΔt,k=0,…N
式中:k表示离散时间序列的第k个时间节点,终端时间为第N个时间节点,即tf=NΔt。
然后将各离散时间节点的控制量u和σ通过M个基函数来表示,即:
式中,φj表示第j个离散点的控制量基函数,pj为待优化的常系数列向量。
本文选取分段常值基函数,且取M=N,则最优控制问题转化为参数优化问题:
则动力学方程(1)可以表示为:
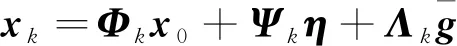
(22)
式中:
式中:
式中:Ac和Bc为连续系统状态转移矩阵和控制输入矩阵;A和B为对应的离散系统状态转移矩阵和控制输入矩阵。
定义如下常值矩阵:
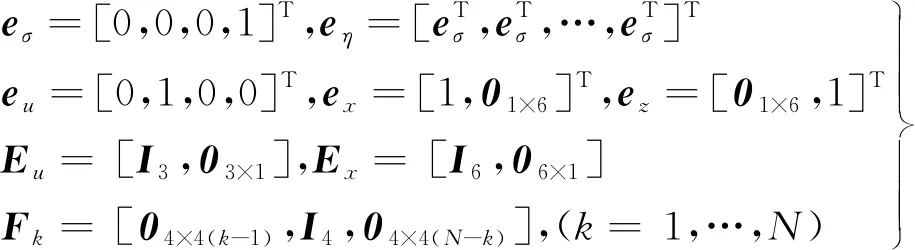
(23)
定义垂直上升段与飞跃段的切换点为k1,飞跃段与垂直下降段的切换点为k2,满足:
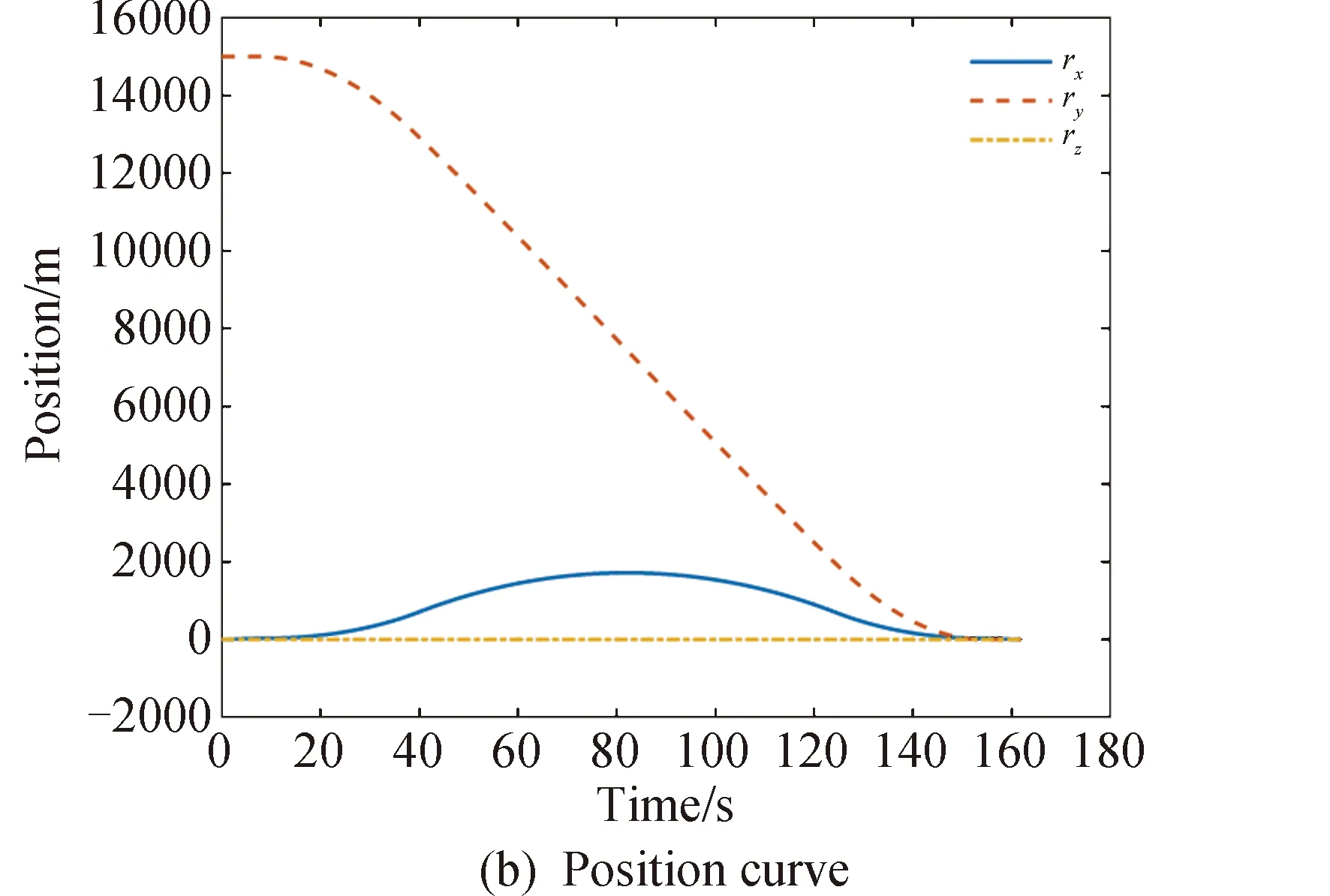
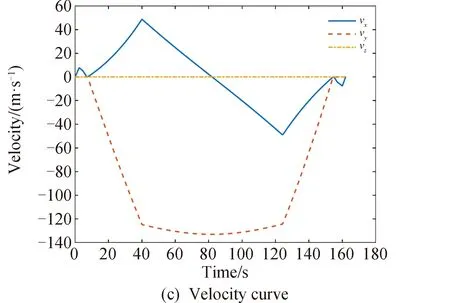
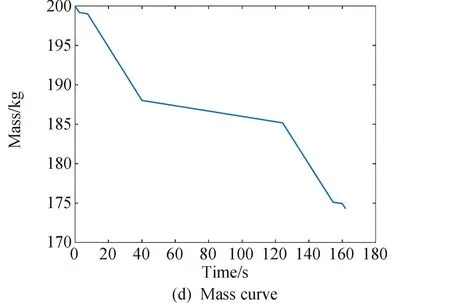
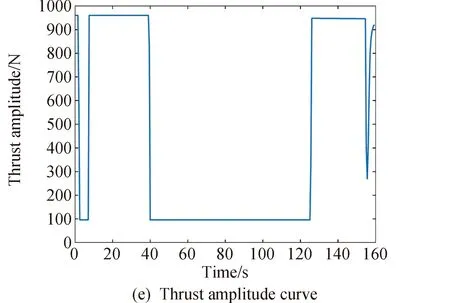
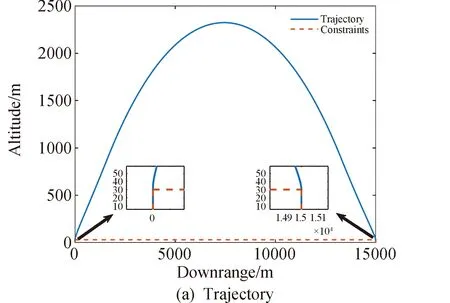
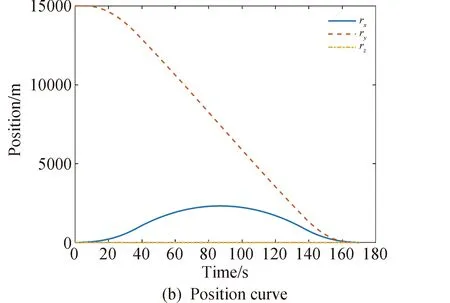
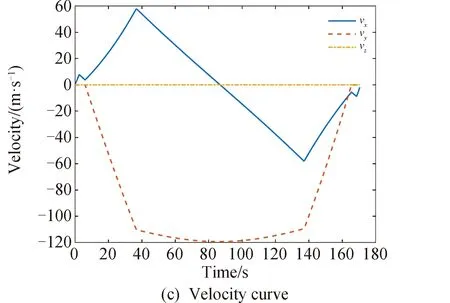
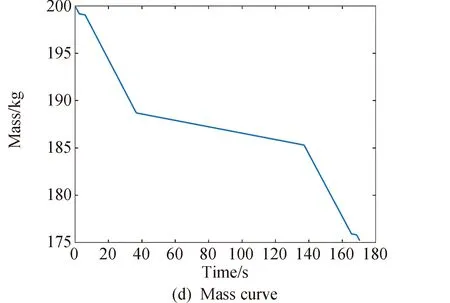
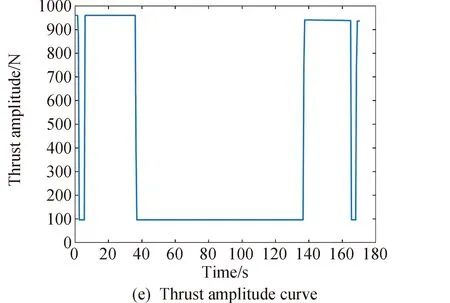
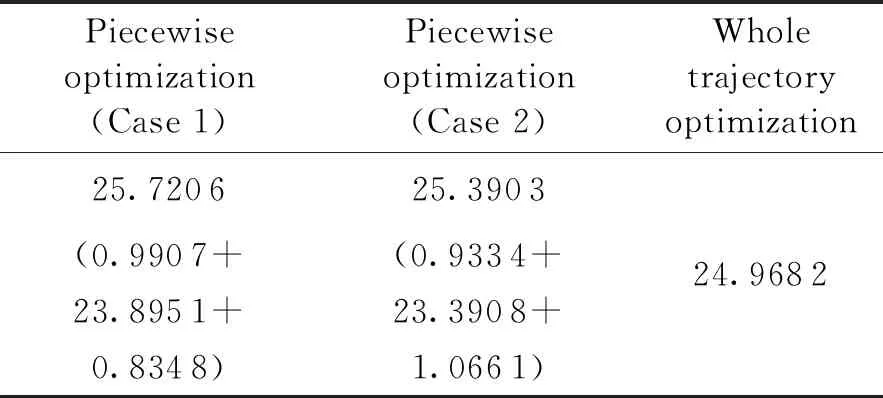
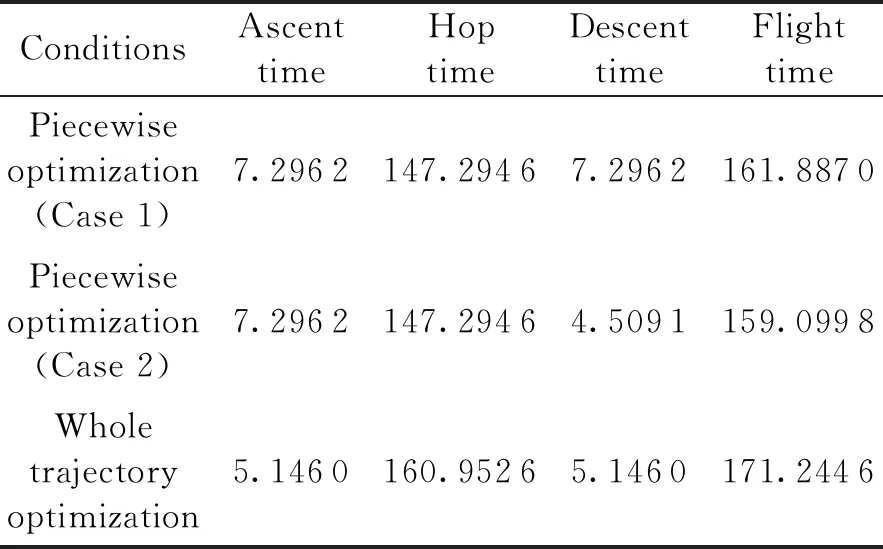
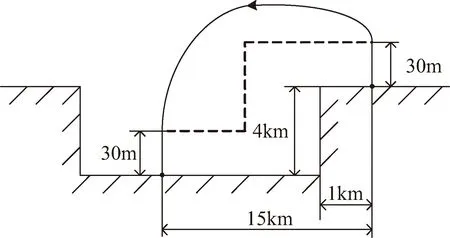
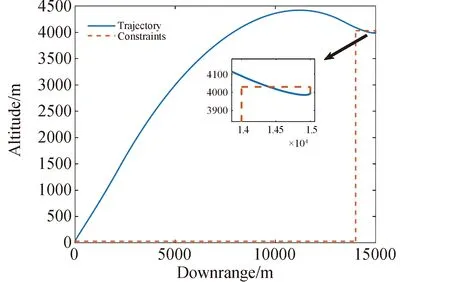
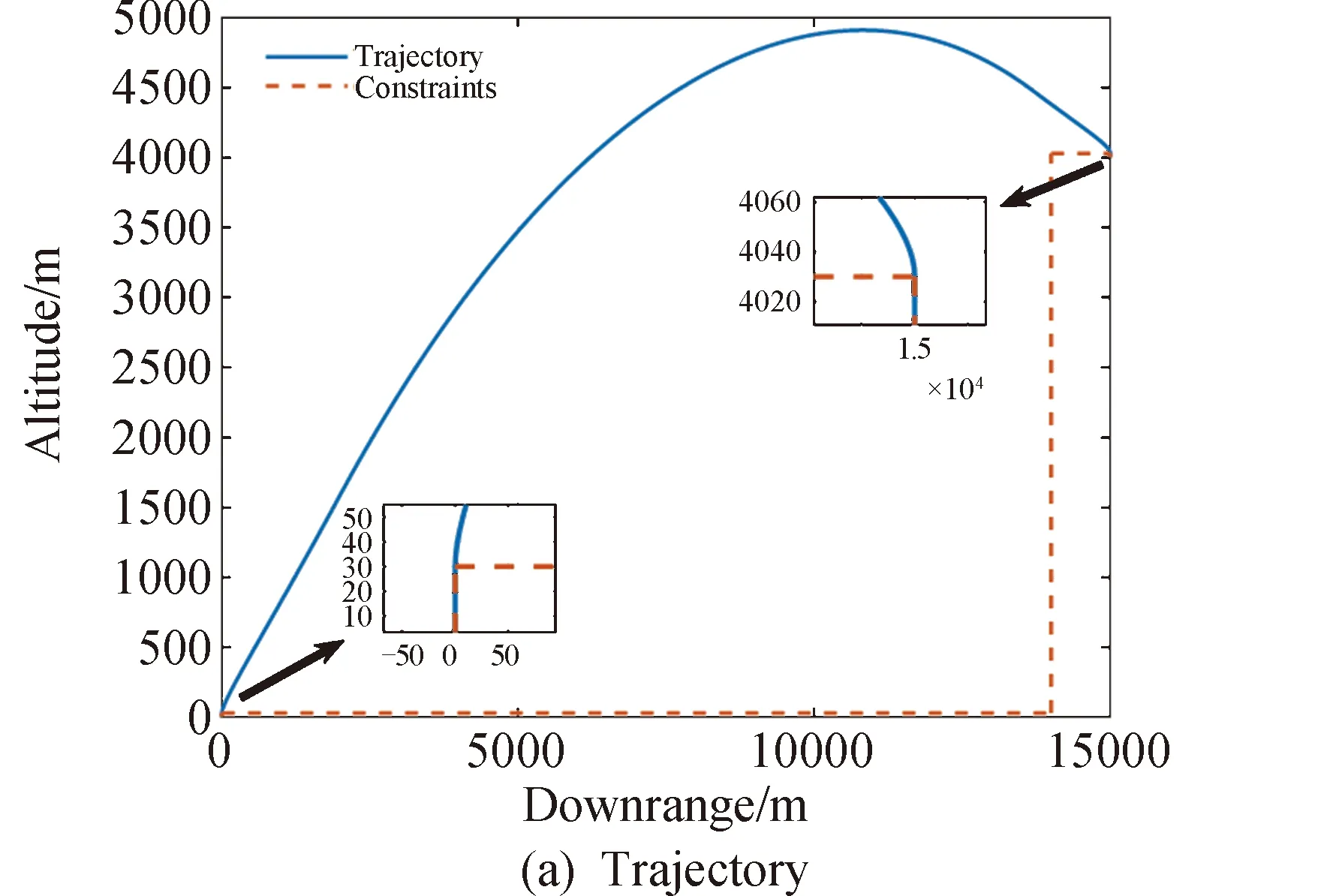
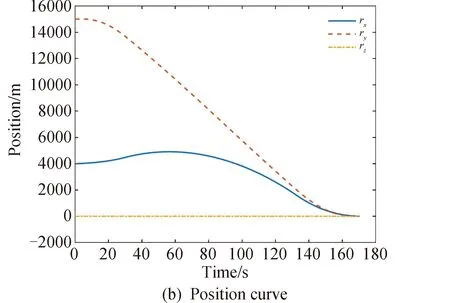
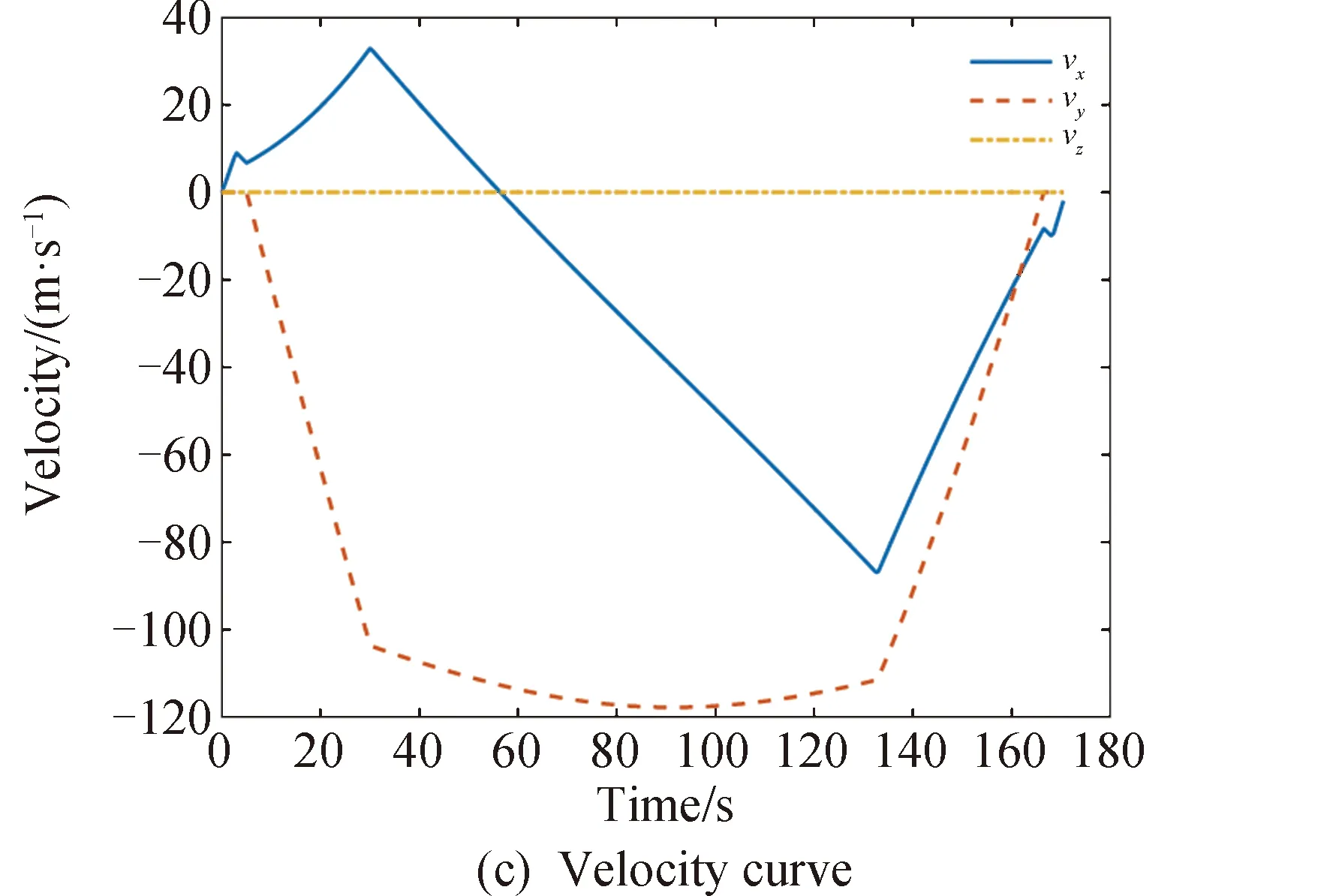
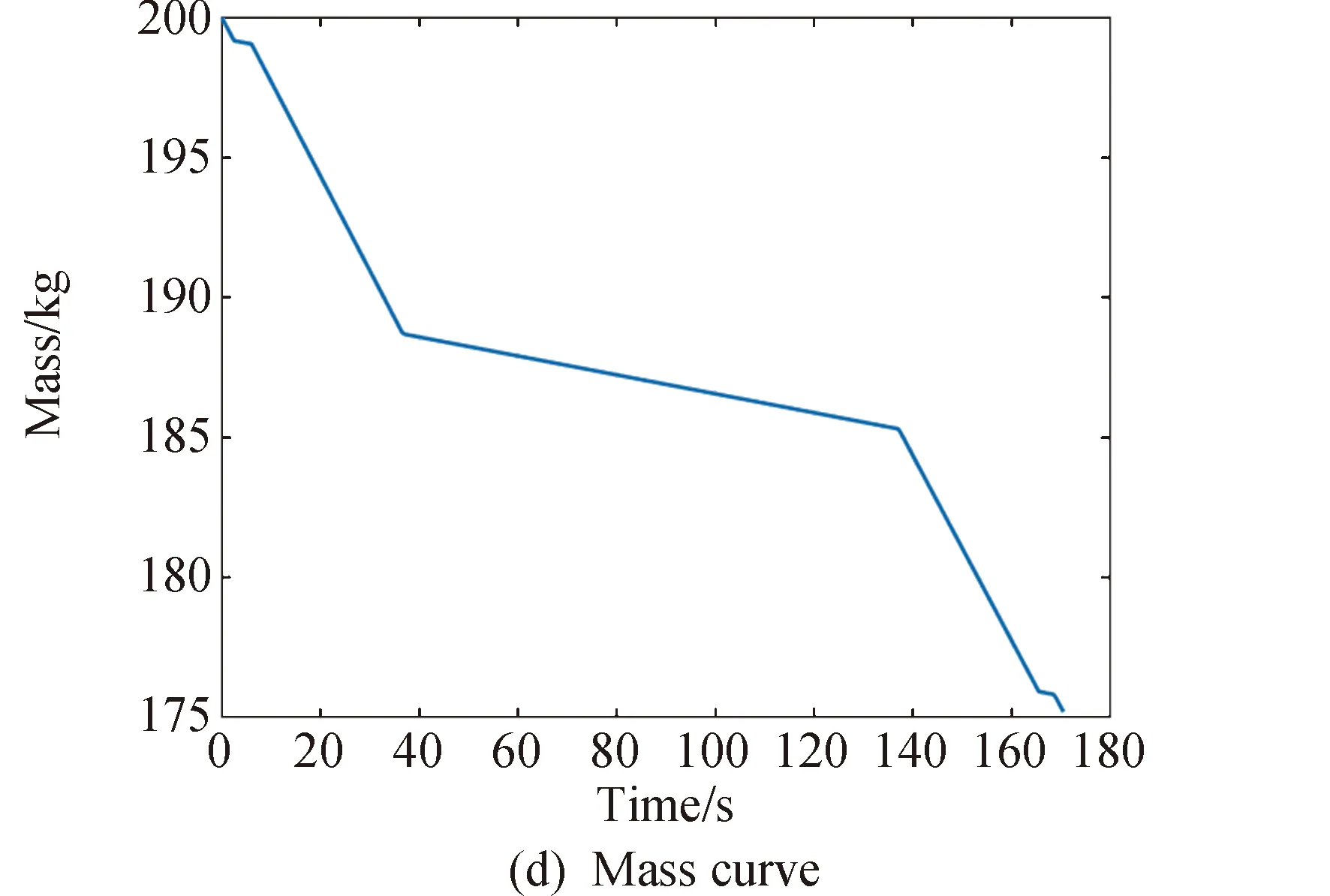
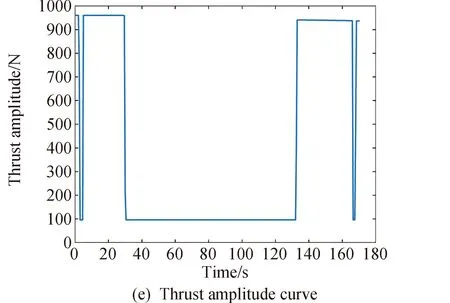
1≤k1 则飞跃轨迹燃耗最优问题最终转化为如下问题。 (1)性能指标 (24) (2)约束条件 (25) (26) (27) (28) (29) 对于任意给定的N,式(24)~(29)定义了一个有限维二阶锥问题,通过使用现有的SOCP算法,可以非常有效地求解,并保证收敛到全局最优解。需要注意到N也是一个解参数,对应运动时间上界tf,且满足0 (30) 式中:mwet为飞跃器总质量;mfuel为燃料质量;α定义见式(2)。 式中:δ为需要调节的参数。 则参数N满足 Nmin≤N≤Nmax 式中: 式中:int为向下取整函数。 为了便于全程凸优化,还需对垂直起飞和着陆段进行约束。利用式(26)对式(25)进行近似处理,首先将2.2节计算出的tas换算为离散时间点k1,在此时间节点前,满足: (31) 在k1点以后的飞跃段,施加如下约束: (32) 垂直下降阶段约束与垂直上升段约束相同: (33) 最终即可把飞跃问题转化为求解SOCP问题,具体的算法步骤见式(34)至式(39),算法流程图见图3。本文算法通过固定上升、下降时间,将分段凸优化问题转化为全程凸优化问题进行求解,因此得到的结果优于分段优化的结果。 (34) 令i=0,转步骤2。 (35) (36) (37) (38) (39) 图3 算法流程Fig.3 Algorithm flowchart 对于已建立的SOCP问题,采用MATLAB求解二阶锥规划问题的工具包YALMIP[22]并借助SDPT3[23]解算器来求解,仿真条件见表1。考虑平地飞跃与向坑内飞跃两种情况进行仿真。 表1 仿真条件 由于本文坐标系OY轴指向起始点,且初始和终端速度都为0,因此任何3维飞跃问题都可以转化到2维平面。若不采用本文的坐标系定义方法,对于3维空间,只需对OZ轴方向进行与OY轴同样的约束,即将式(23)中eu向量改为[0,1,1,0]T,并适当增加飞行时间上界即可。 考虑如图4所示工况,其中虚线为半矩形约束,飞行轨迹不能落在该区域内。为进行燃耗的比较,考虑了分段凸优化和全程凸优化两种情况。 图4 月球飞跃轨迹Fig.4 Hop trajectory on the Moon (1)分段凸优化 将运动轨迹分为三段,分别进行凸优化求解燃料最优轨迹。起始点位置为r0=[0,15000,0]T,速度为v0=0,上升段为从月面垂直起飞到30 m高处悬停。飞跃段的初始位置为r1=[30,15 000,0]T,初始速度为v1=0,飞跃过程保持高度大于30 m,横向移动15 km,即末端位置为r2=[30,0,0]T,末端速度为v2=0。着陆段为从高度30 m垂直着陆到月面,即rf=0,vf=0。仿真结果如图5所示,其中虚线为30 m高度半矩形约束。 从图5可以看出,飞行轨迹满足半矩形约束;飞跃器先加速到一定速度后,发动机关机进行滑行,直到接近目标点后重新开机制动;由推力曲线可以看出,推力幅值在每个阶段都呈最大-最小-最大的趋势。 图5 平地飞跃分段凸优化的第一种情况Fig.5 The first case of piecewise convex optimization of flat hop 续图5 Fig.5 Continued 第二种情况考虑了放宽飞跃段的末端速度约束,假设飞跃段末端飞跃器的质量仍为200 kg,如果采用最大推力着陆,容许速度为: (40) 式中:vh为高度方向的容许速度;Tmax为最大推力;假设质量m恒定,因此加速度a恒定。 由式(40),并考虑一定的工程余量,设置飞跃段末端垂向下降速率小于10 m/s,并将上升段末端速度v1设为自由,仿真结果如图6所示。 图6 平地飞跃分段凸优化的第二种情况Fig.6 The second case of piecewise convex optimization of flat hop (2)全程凸优化 采用本文所提出的算法进行仿真,结果如图7所示。表2列出了三种仿真条件下的燃料消耗,可以看出,放宽垂直上升段和飞跃段的末端约束可以减少燃料消耗,但总的来说,分段凸优化的燃料消耗始终高于全程凸优化的方法,这主要是因为全程凸优化是综合考虑了所有约束,而分段凸优化只能保证在每个阶段的燃耗是最优的。 图7 平地飞跃全程凸优化仿真结果Fig.7 Full trajectory convex optimization simulation of flat hop 表2 平地飞跃不同条件下的燃料消耗 表3列出了三种仿真条件下的飞行时间。 表3 平地飞跃不同条件下的飞行时间 可以看出两种分段凸优化的总飞行时间相差不大,而全程凸优化方法在飞跃段的飞行时间多于分段凸优化方法,这是因为更低的燃耗意味着用了更多时间的最小推力,因此增加了飞行时间。此外,注意到搜索得到的最优时间并不在给定搜索范围的边界处,因此在计算垂直上升、下降段时间的搜索边界时,不考虑质量变化是合理的。 为进一步校验算法的有效性,考虑如图8所示工况,虚线为半多边形约束,除垂直上升段和着陆段外,飞行轨迹不能与该半多边形相交。 图8 向坑内飞跃轨迹Fig.8 Hopping into the pit 首先直接用之前的算法进行仿真,得到如图9所示结果。可以注意到在初始段违反了约束,因此要对约束条件进行修改。而由前面的仿真可知,飞跃器横向运行1 km的时间为30 s,因此在全程凸优化框架内,对离散化后的前60个节点,增加约束使其高度大于4 030 m,仿真结果如图10所示。可以看出,运动轨迹满足约束,最优燃耗为25.069 2 kg,总飞跃时间171.244 6 s。由此工况可知,对本文算法的拓展应用只需根据实际情况修改式(31)~(33)参数即可。 图9 坑内飞跃运动轨迹Fig.9 Trajectory of hopping into the pit 图10 坑内飞跃仿真结果Fig.10 Simulation of hopping into the pit 续图10 Fig.10 Continued 本文研究了飞跃器转移过程中的燃料最优轨迹设计问题,通过对凸优化方法进行扩展,求解燃料最优问题从而得到最优轨迹。 1)算法通过假设垂直上升和下降段时间相同,利用黄金分割法搜索得到了上升、飞跃和下降段的时间,能将原问题中的非凸约束转化为凸约束。 2)算法能在满足约束的情况下实现精确飞跃转移。对于平地飞跃情况,相同仿真参数下其燃耗为24.968 2 kg,优于两种不同速度约束条件下分段凸优化的结果。 3)坑内飞跃的仿真结果表明,对于不同的工况,只需根据实际情况修改算法中的期望高度值,利用本文思想重新分段,便可得到燃耗最优轨迹。 由于考虑到计算效率的问题,本文算法近似了实际的上升、着陆段的飞行时间,因此,在不提升计算复杂性的情况下,精确考虑不同阶段飞行时间的燃料最优解将是下一步的研究方向。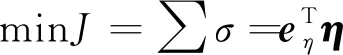
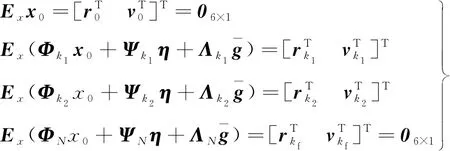
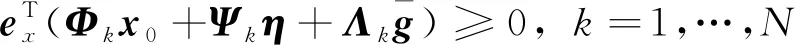
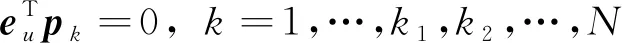
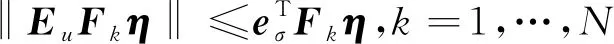
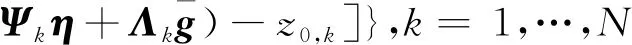
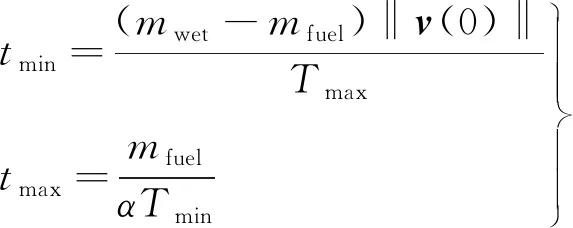
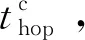
2.4 飞跃全程的凸优化算法
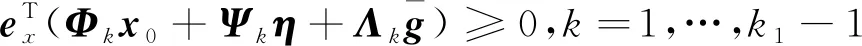
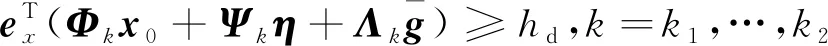
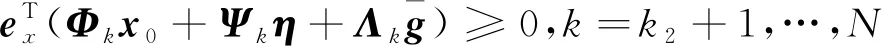



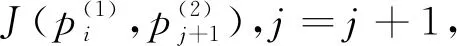


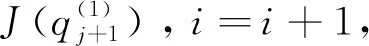
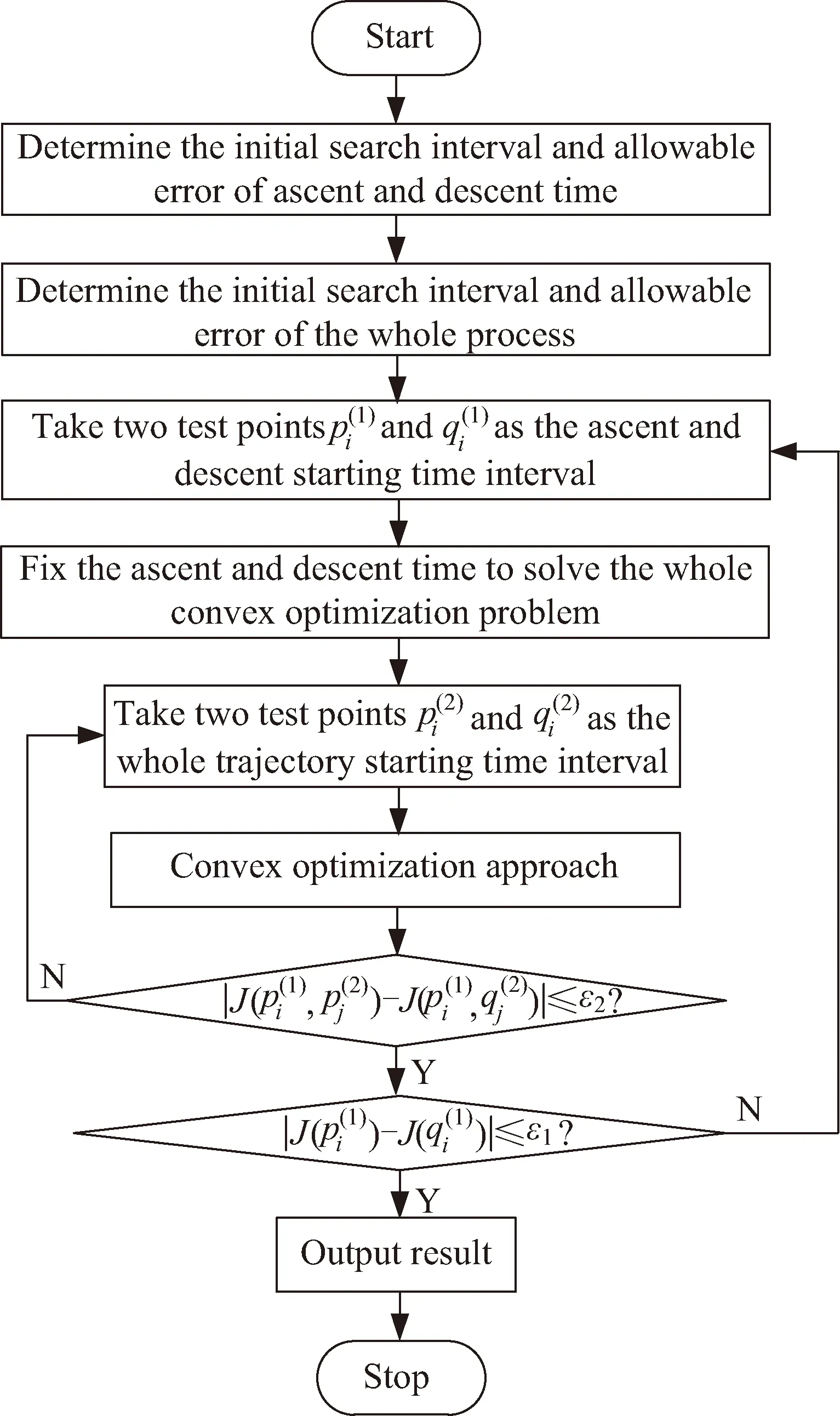
3 仿真校验

3.1 平地飞跃
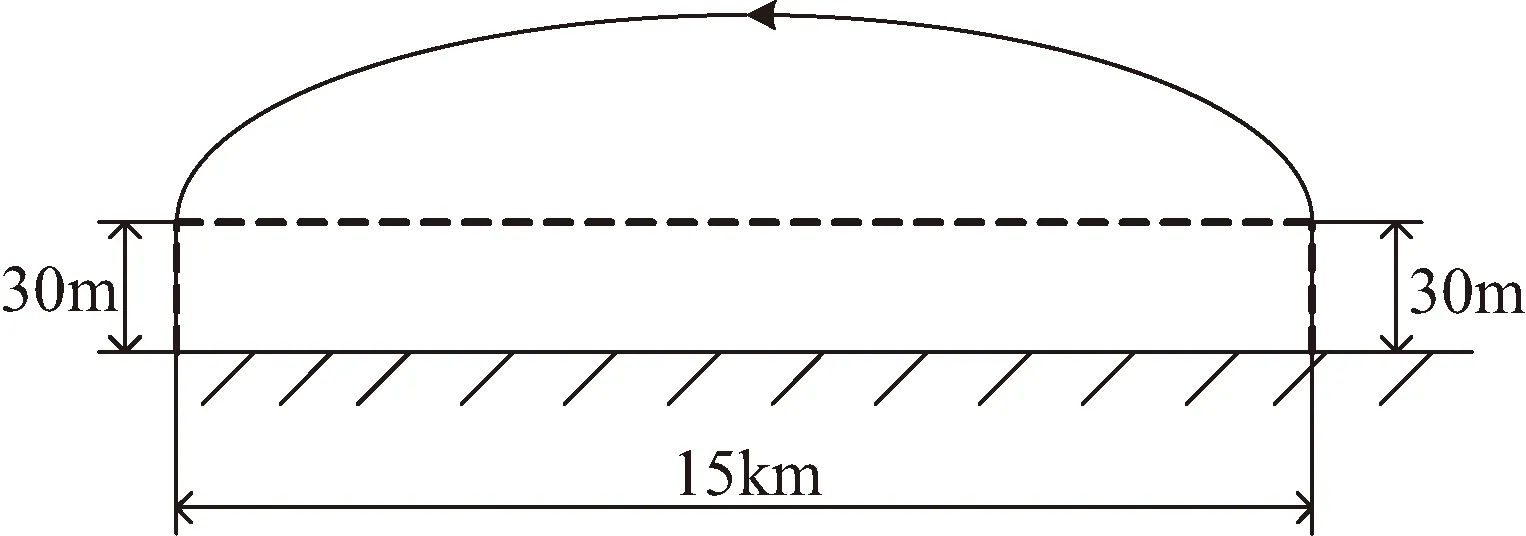
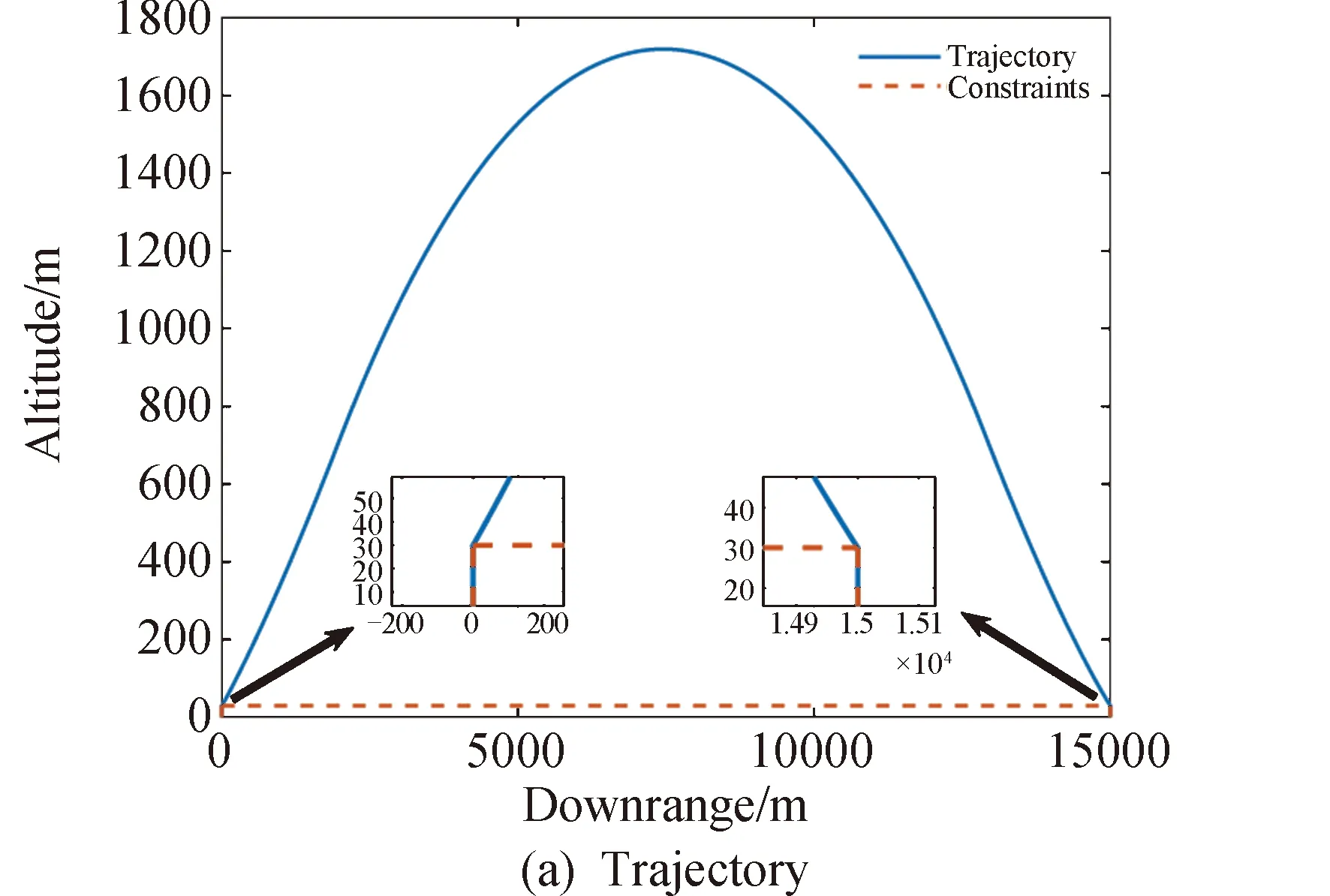

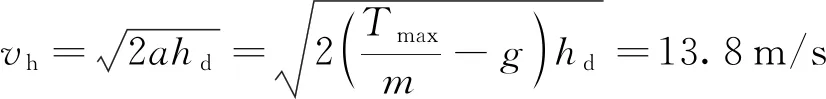
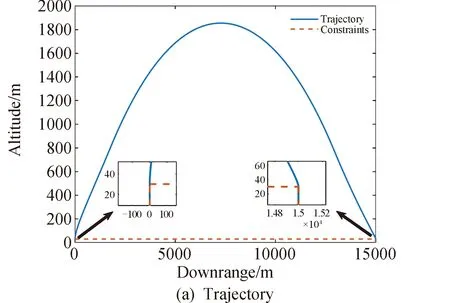
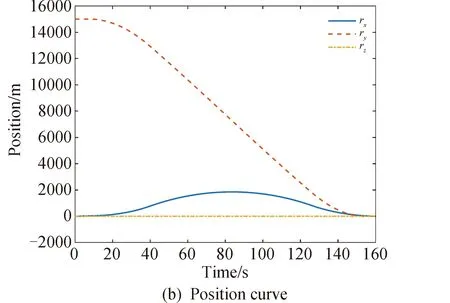
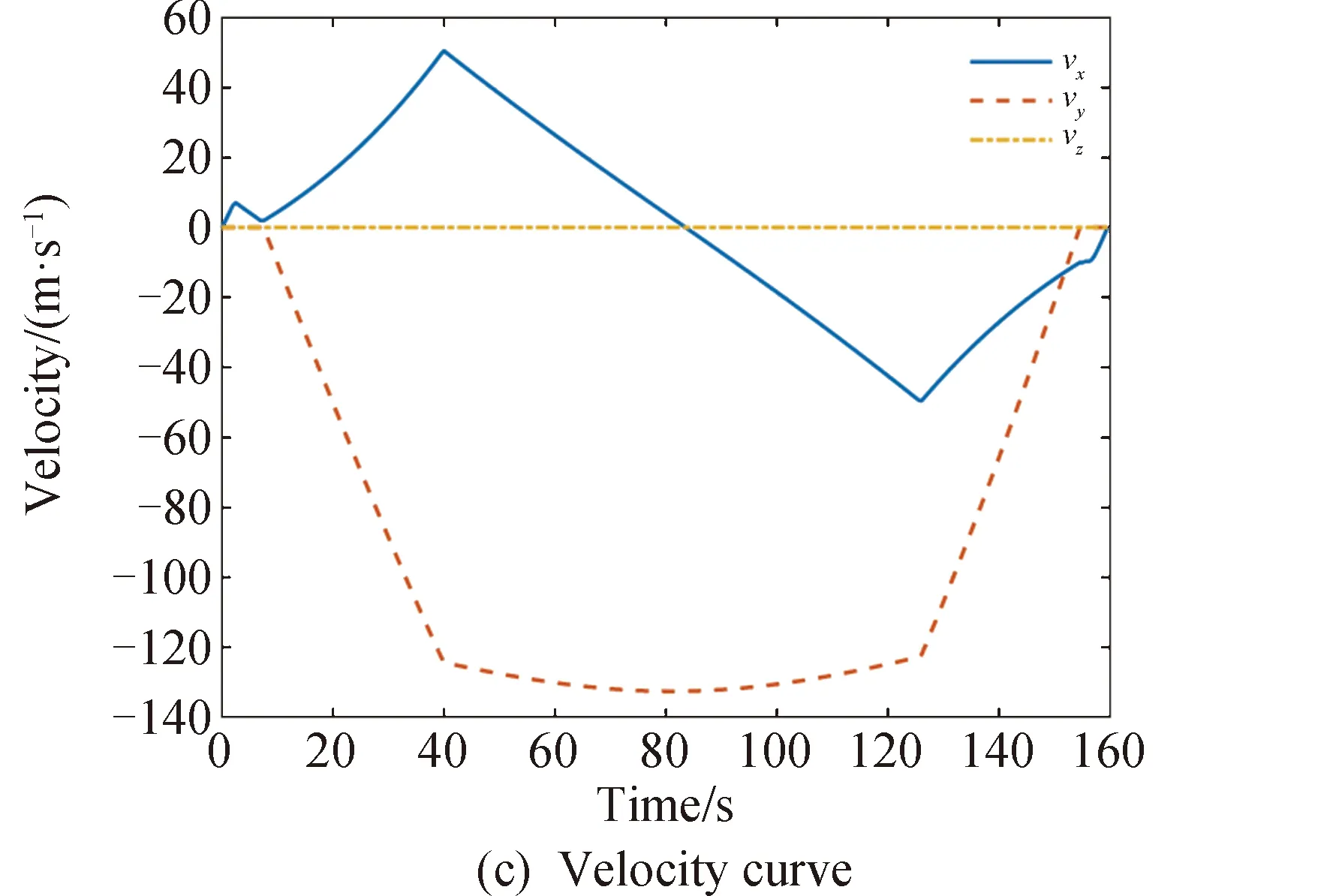
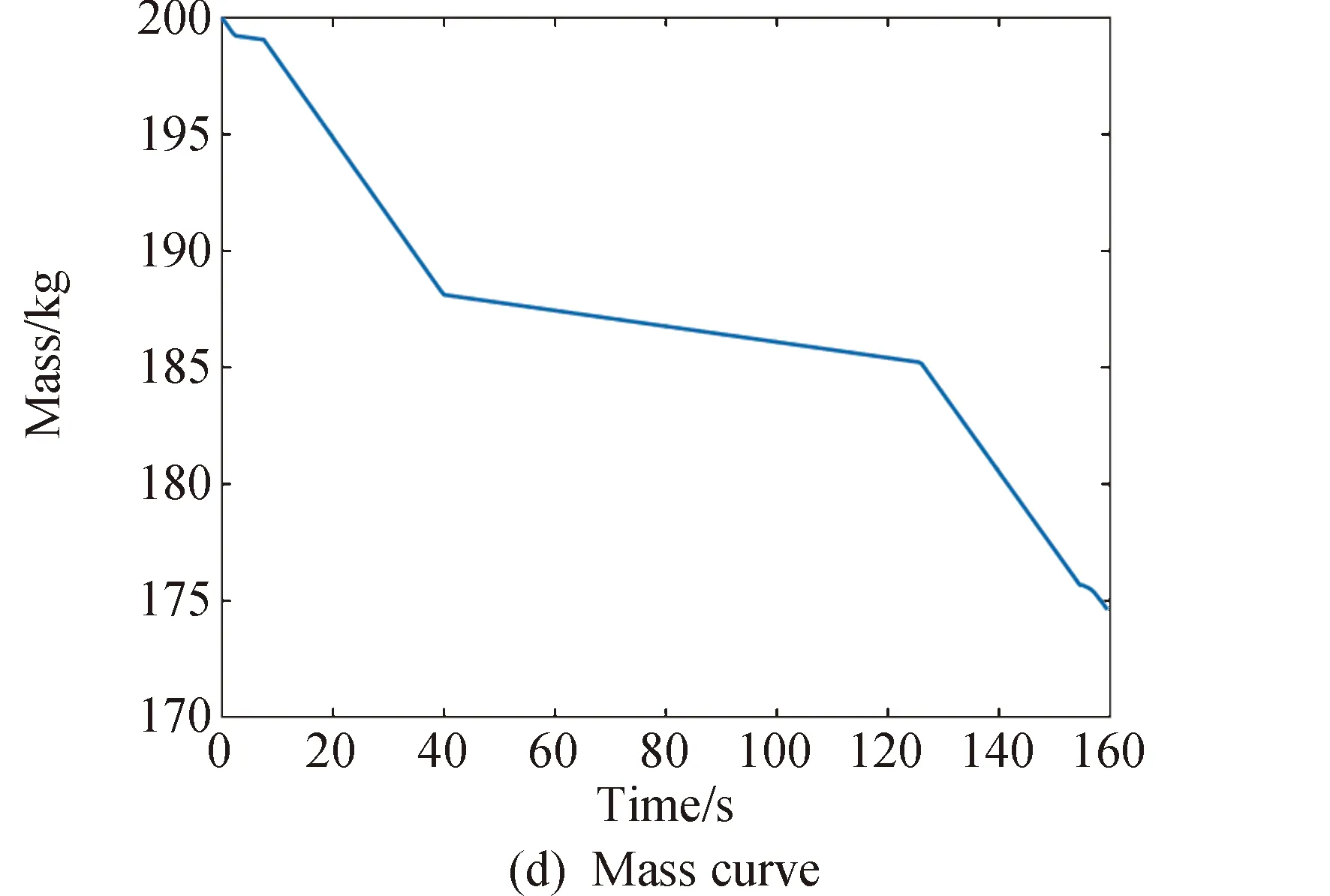
3.2 坑内飞跃
4 结束语
