基于Neyman-Pearson准则的空间目标轨道机动检测方法
2021-05-21王庆瑞邹江威吴文振陈健
王庆瑞,邹江威,吴文振,陈健
国防科技大学 自动目标识别重点实验室,长沙 410073
随着世界各国对太空探索的逐步深入,航天任务日益频繁,空间目标种类与数量不断增加,太空环境变得愈加复杂[1-2],快速且准确的轨道机动检测成为保障空间目标运行安全的重要需求[3-4]。
国内外学者从不同角度对空间目标机动检测进行了研究。Kelecy等[5]利用最小二乘法与卡尔曼滤波法研究了脉冲小推力作用下的机动检测,并分析比较了两种方法的性能,但缺少可操作的检测流程。Lubey等[6]利用最优控制估计方法,通过计算控制距离度量实现脉冲推力与连续推力作用下的机动检测,其计算过程中的动态不确定性参数需要手动调整。国内董云峰等[7]率先提出利用小波分析工具实现轨道机动检测,根据小波系数曲线随小波分析尺度的变化趋势判定是否存在轨道机动。张振军等[8]通过比较小波分解后信号的相关系数阈值来判断轨道机动。苏建敏等[9]通过将小波分解后信号的平均值与给定阈值进行对比,检测目标卫星轨道机动。上述利用小波分析工具检测轨道机动,对于如何获取合适的判断阈值,缺乏定量的推导与分析,实用性尚有欠缺。崔红正等[10]利用观测值残差比对不同推力下的机动进行了研究,对工程应用有较好的参考价值。
针对脉冲小推力下的轨道机动检测问题,本文提出了一种基于Neyman-Pearson (NP)[11-12]概率判决模型的检测方法。该方法能够根据某段测量数据的概率密度函数与设定的虚警概率,自适应地生成判决门限,实现卫星变轨的有效检测。采用滑窗策略,该方法能够对整段测量数据实现持续性检测,得到变轨发生的大致时间。文中首先介绍了变轨检测的原理,然后给出了相应的变轨检测步骤,最后通过不同机动幅度下目标卫星变轨检测的仿真实验,验证了该方法的有效性。
1 特征量建模
利用星载平台对目标卫星进行观测的场景如图 1所示,伴飞卫星与目标卫星相隔一定距离,同方向飞行,利用伴飞卫星上搭载的激光测距雷达[13]测量与目标卫星的相对距离,记为r0。
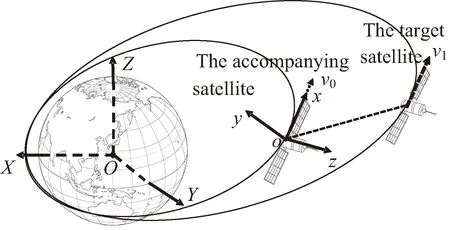
图1 激光雷达测距示意图Fig.1 Schematic diagram of lidar ranging
考虑到实际中星载激光雷达存在一定的测量误差,测量得到的目标卫星相对距离为:
r=r0+w
(1)
式中:w为随机测量误差,设w满足高斯同分布,标准差为σ。目前工程上使用的星载激光雷达测距精度已经达到毫米量级[14],但考虑到实际中跟踪误差等不利因素的影响,本文设定测量噪声的标准差为σ=0.05 m。
对相对距离r进行差分处理得到距离变化率V为:

(2)
当目标卫星未发生轨道机动时,相对距离在一定时间内是连续变化的,距离变化率V趋近平滑。当目标卫星发生轨道机动时,由于目标卫星受到脉冲推力作用,其速度发生突变[10],即目标卫星相对伴飞卫星的距离变化率发生突变,此时距离变化率具有阶跃信号特征[8],因此可以将距离变化率作为特征量用于变轨检测。
2 机动检测方法原理
目标卫星轨道机动的检测问题可抽象为对信号V的阶跃突变检测问题。但由于测量噪声的存在,使得信号V的阶跃特征被淹没在噪声中,无法直接检测出来。本节以NP检验模型为基础,构建机动检测方法,检测包含测量噪声的信号V是否发生阶跃突变。
2.1 NP检验模型
NP准则可用于检验某信号序列是否发生整体性偏移。设该信号序列为x,序列中各信号的概率密度分布函数已知,不妨设他们满足等方差的正态分布。基于NP准则对序列x构造假设性检验如下:
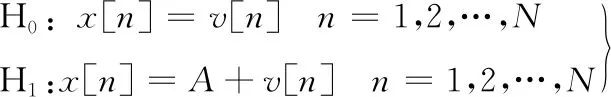
(3)
式中:H0是零假设;H1是备选假设;幅度A表示序列的整体偏移,为未知常数;序列v服从期望为μ[n](n=1,2,…,N)、等方差σ2的独立正态分布。序列x在H1、H0条件下的概率密度函数分别记为p(x;A,H1)与p(x;H0)。定义似然比:
(4)
似然比描述了对于序列x,H1的可能性与H0的可能性的比值。如果
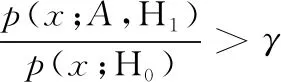
(5)
那么检测器判决为H1,其中γ为门限。将式(4)代入式(5),两边取对数得:
假定A>0,化简得:
将上式乘以系数1/N,得到序列x的均值,记为检验统计量T(x):

(6)
记

(7)
其中γ′为新门限,得到:

(8)
式(7)说明了序列偏移量A与门限γ′的定量关系,但由于A为未知常数,无法通过式(7)解算出γ′。从另外一个方面,可以根据T(x)的概率密度函数,结合虚警概率PFA约束求解门限γ′。由于序列x为等方差的独立正态分布,其均值T(x)也服从正态分布,T(x)的期望与方差分别为:
根据T(x)的正态分布特征,得到虚警概率PFA、检测概率PD和门限γ′的关系为:


(9)

(10)
根据式(9),在虚警概率约束下求解门限γ′:
(11)
当T(x)>γ′,判决为H1,此时为正确检测;判决为H0,此时为虚警。将式(11)代入式(10)可得:

(12)
式中:Q为右尾函数,单调递减;Q-1为其逆函数,单调递增。上式表明,对于给定的PFA,检测性能随着NA2/σ2单调递增,这里将NA2/σ2定义为阶跃能量噪声比,用来描述阶跃能量和信号方差的大小关系。
同理,当A<0时,给定虚警概率下的检测门限和检测概率分别为:
(13)
PD=Pr {T(x)<γ″;H1}
(14)
值得注意的是,式(11)与式(13)的第一项互为相反数,第二项相同。这是因为T(x)服从正态分布,其概率密度函数是左右对称的,对称中心为T(x)的期望。因此A>0与A<0时的检测问题是等效的,两种情况下的检测概率表达式相同。
2.2 卫星轨道机动检测方法
依据上文的NP模型,采用距离变化率序列{V(n),n=1,2...,S}对卫星的脉冲小推力轨道机动进行检测。从整段数据序列中抽取一段作为待检测数据,将待检测的某段数据分为前后两段,假定前半段数据中目标卫星未发生变轨,作为参考窗口;后半段数据中目标卫星可能发生了变轨,作为检测窗口。通过对参考窗口数据进行多项式拟合、外推,然后与检测窗口轨道数据特征进行对比,实现目标卫星轨道机动检测。
首先在序列V(n)确定位置相邻的参考窗口和检测窗口,长度分别为M和N,它们的关系设定为:
参考窗口:R(n)=V(n),n=n0,n0+1,n0+2,n0+3, …,n0+M-1。
检测窗口:D(n)=V(n),n=n0+M,n0+M+1,n0+M+2, …,n0+M+N-1。
设参考窗口中目标卫星未发生变轨,根据距离变化率平滑变化这一先验信息,估计数据的测量方差。利用最小二乘法对R(n)进行多项式曲线拟合得到距离变化率期望的估计值r(n),r(n)和R(n)之间的差值为测量误差。在独立同分布的高斯白噪声模型下,测量误差的方差估计值为:
若检测窗口中目标卫星未发生变轨,则检测窗口中的数据和参考窗口中的数据具有相同的变化趋势,两部分的期望值满足相同的多项式曲线参数。因此将参考窗口内的多项式曲线进行外推,得到检测窗口中数据检验统计量的估计值为:

(15)


(16)
设定虚警概率为PFA,根据(11)、(13)得到A>0与A<0两种情况下的变轨判决门限分别为:

(17)

(18)
检测窗口内检验统计量的实际值为:

(19)
将T(D)和变轨判决门限进行对比,若

则认为目标在检测窗口内已经发生了变轨。
上述讨论的是针对固定参考窗口R(n)和检测窗口D(n)的变轨检测问题。将参考窗口和检测窗口的位置在序列观测数据V(n)上进行滑动,可实现对目标卫星变轨的连续检测,检测流程如图 2所示。

图2 检测流程Fig.2 Flow chart of detection
3 卫星轨道机动检测仿真
3.1 构造检测信号
本文采用STK软件仿真卫星运行轨道[15-17],并获取目标卫星和伴飞卫星之间的相对距离,伴飞卫星与目标卫星的初始轨道参数设置如表 1所示,其中a,e,i,Ω,ω,f为经典轨道六要素的半长轴、偏心率、倾角、升交点赤经、近地点俯角和真近点角[18-19]。仿真卫星轨道运行时间为300 s,激光测距雷达每隔0.1 s采集一次相对距离数据。

表1 卫星初始轨道参数
当目标卫星运行到200 s时,在目标卫星运行速度方向施加脉冲小推力,使该方向速度增量为I=0.3 m/s。目标卫星和伴飞卫星之间的相对距离如图 3所示。可见伴飞卫星逐渐靠近目标卫星,相对距离近似为线性减小;但由于卫星变轨的幅度较小,不能从相对距离曲线中观察出目标卫星是否发生轨道机动。

图3 相对距离示意Fig.3 Diagram of relative distance
对相对距离量进行差分处理,得到目标卫星相对伴飞卫星的距离变化率如图4所示。可见当目标卫星发生变轨时,距离变化率有一个明显的阶跃突变特征。对比相对距离量,目标卫星轨道机动特征在距离变化率序列中的表现更加明显,因此将后者作为特征量用于轨道机动检测是合理的。
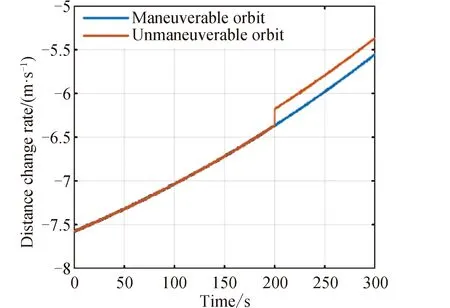
图4 相对距离变化率示意Fig.4 Diagram of relative distance change rate
包含测量噪声的距离变化率,如图5、图6所示。从图中可知,由于测量噪声的存在,使得距离变化率的阶跃突变特征被淹没在噪声中,无法直观地判断目标卫星是否发生轨道机动。
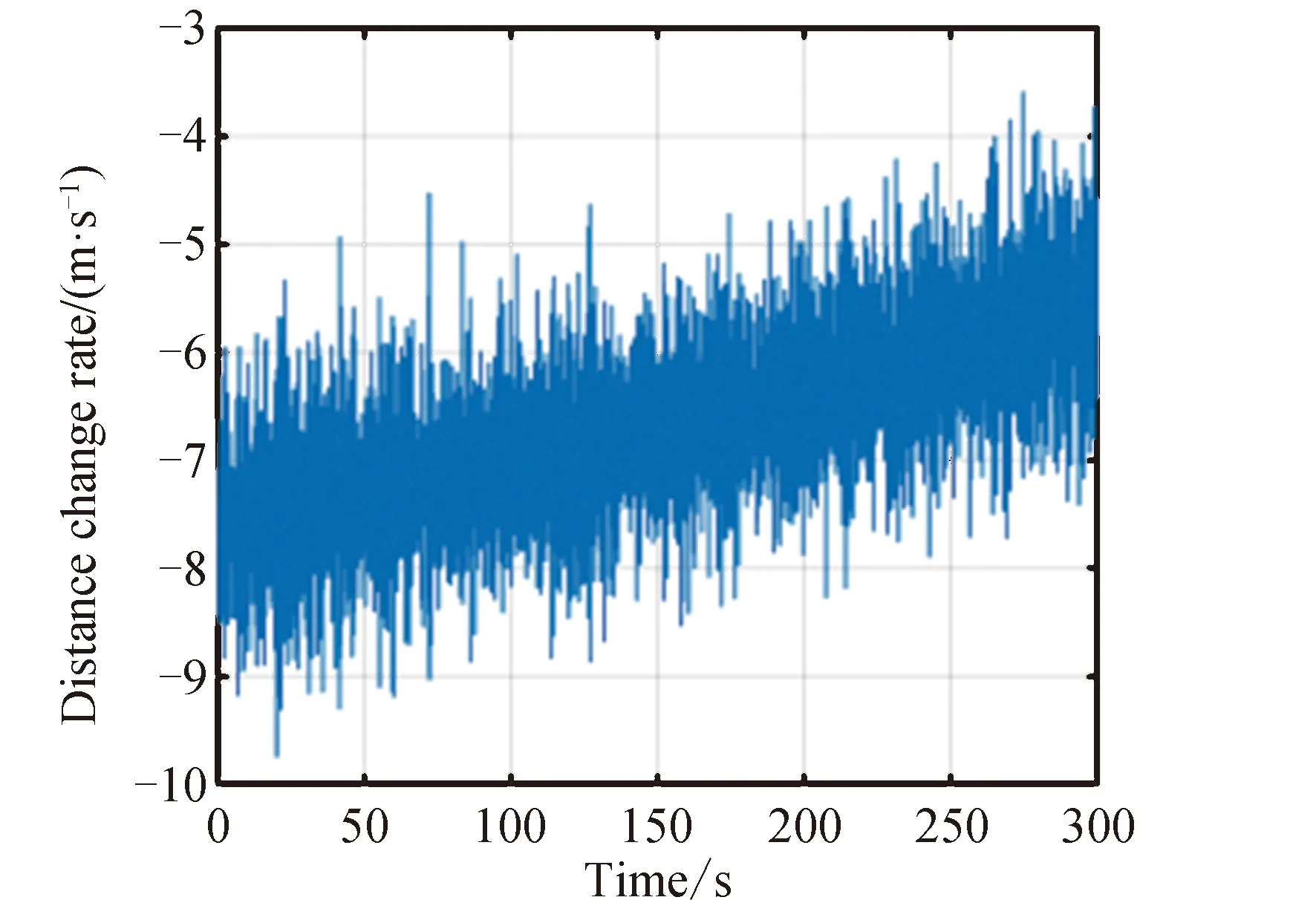
图5 未变轨时包含测量噪声的距离变化率Fig.5 The distance change rate when the measured noise is included without orbit change

图6 变轨时包含测量噪声的距离变化率Fig.6 The distance change rate when the measured noise is included with orbit change
3.2 基于NP准则的轨道机动检测
设定参考窗口的长度M=1 300,检测窗口长度N=100。选取图 6中一段数据进行变轨检测,利用最小二乘法对参考窗口内的数据进行多项式曲线拟合,多项式次数设定为2,而后将曲线外推至检测窗口,如图7所示。
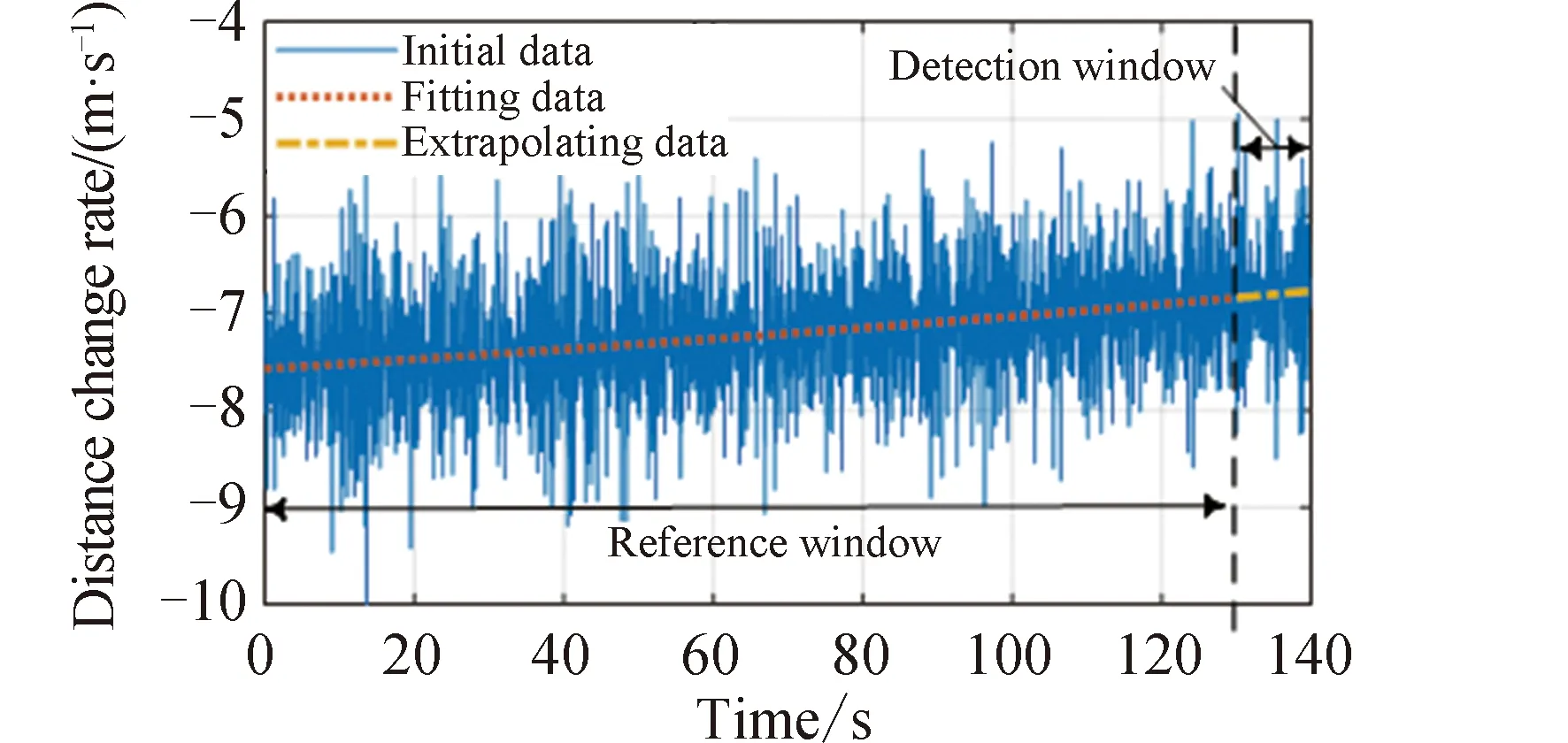
图7 数据多项式拟合、外推结果Fig.7 The results of data polynomial fitting and extrapolation
设定虚警概率PFA=10-2,针对图6中的数据,其检验统计量T(D)与判决门限的关系,如图8所示。
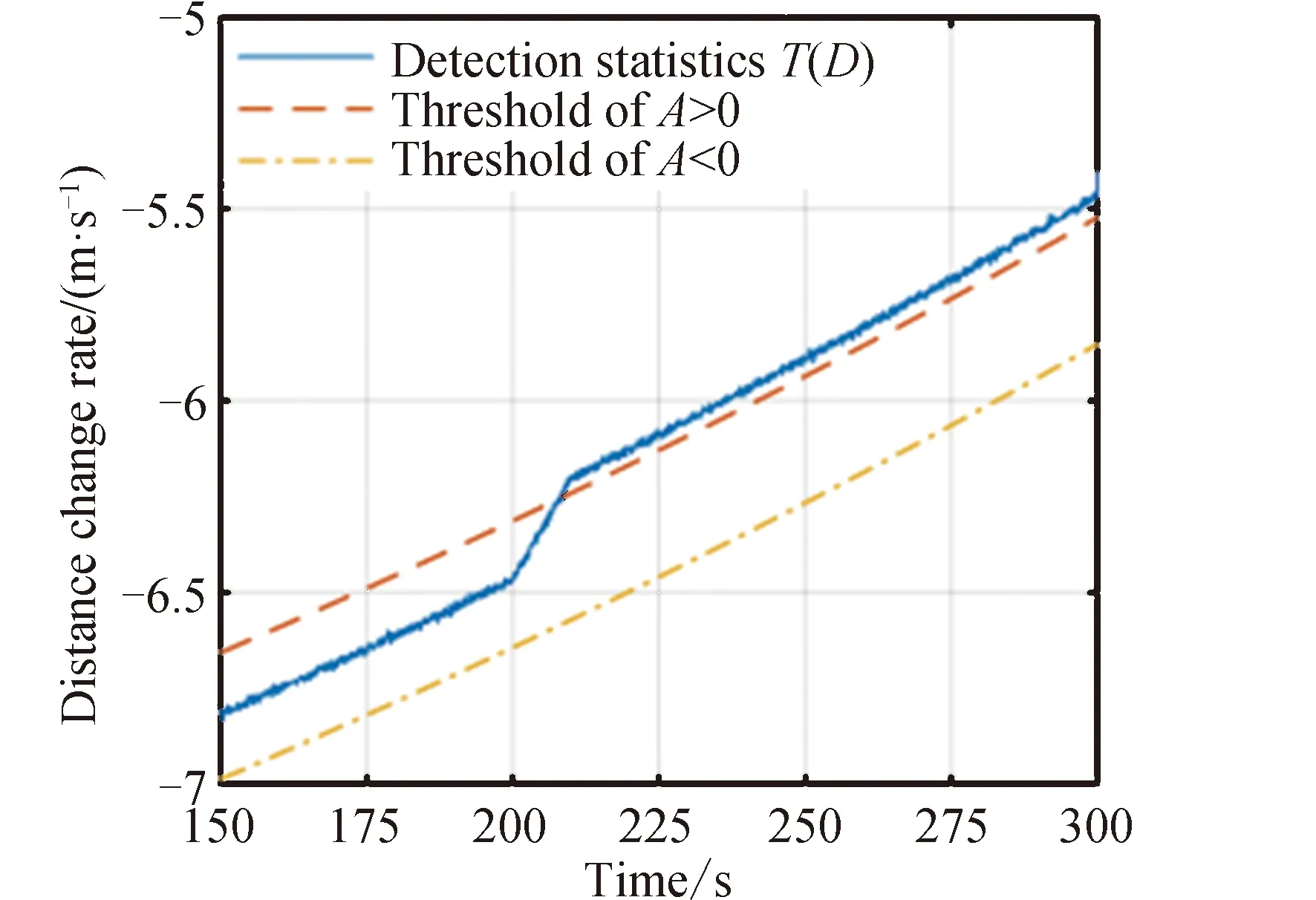
图8 检验统计量与门限值的对比(N=100,I=0.3 m/s)Fig.8 The comparision between test statistics and threshold values(N=100,I=0.3 m/s)
将检测窗口长度修改为N=200,其他参数保持不变,仿真得到检验统计量T(D)与变轨判决门限,如9所示。

图9 检验统计量与门限值的对比(N=200,I=0.3 m/s)Fig.9 The comparision between test statistics and threshold values(N=200,I=0.3 m/s)
设速度增量I=-0.3 m/s,其他参数保持不变,仿真得到检验统计量T(D)与变轨判决门限,如10所示。

图10 检验统计量与门限值的对比(N=100,I=-0.3 m/s)Fig.10 The comparision between test statistics and threshold values(N=100,I=-0.3 m/s)
根据式(8),在滑窗策略下将距离变化率转化为检验统计量,实际上是一个滤波过程。对比滤波前后的距离变化率曲线可见,滤波有效抑制了噪声干扰,滤波后的阶跃突变特征十分明显。图8与图9中设定的脉冲速度I相同,对比两者的检测效果可得,检测窗口宽度较大时,距离变化率的阶跃特征更容易被检测出来,但大检测窗口导致信号阶跃突变过程变长,检测实时性降低。图8与图10的变轨检测结果表明,在加速和减速的情况下,该检测方法均能有效检测出目标卫星轨道机动。
3.3 机动检测效果影响因素
不同窗口宽度参数下,阶跃能量噪声比随着阶跃幅度|A|变化的曲线如图11所示。从图中可知,相同的变轨幅度|A|情况下,检测窗口宽度越大,阶跃能量噪声比越大。

图11 幅度|A|与阶跃能量噪声比关系Fig.11 The relationship between amplitude|A| and the of step energy to noise of ratio
根据式(12)计算得到阶跃能量噪声比、虚警概率PFA与检测概率PD的关系,如图 12所示。

图12 阶跃能量噪声比与检测概率关系Fig.12 Relationship between the step energy-to-noise ratio and detection probability
图12表明,当虚警概率PFA一定时,阶跃能量噪声比与检测概率PD成正相关关系,即目标卫星的变轨幅度越大,测量噪声越小,其轨道机动越容易被检测出来。选取虚警概率PFA=10-2,当阶跃能量噪声比≥10 dB时,检测概率PD达到0.80以上。对应在窗口宽度N=100与N=200情况下,当幅度|A|分别大于或等于0.3与0.2时,能有效检测出目标卫星轨道机动。
4 结束语
针对脉冲小推力作用下的卫星变轨检测问题,本文提出了基于NP概率判决模型的检测方法,有效抑制了目标卫星测距误差的不利影响。该方法根据伴飞卫星和目标卫星之间相对速率数据的波动特征,与设定的虚警概率,能够自适应生成变轨判决门限,实现轨道机动检测。通过对检测数据作滑窗处理,可以实现持续性检测,并估计出变轨发生的时间。本文方法根据测量数据本身的特征自适应地生成变轨判决门限,相比于之前的方法具备更强的实用性。
文中通过公式推导与仿真模拟,获得了虚警概率、检测概率、机动程度与测量噪声之间的定量关系。研究表明,在给定虚警概率条件下,当目标卫星机动幅度一定时,测量误差越小,检测窗口宽度越大,阶跃能量噪声比会越高,对目标卫星轨道机动的检测概率越大。变轨检测是获取目标卫星轨道机动特征的第一步,我们后续的研究将在检测目标轨道机动的基础上,进一步估计轨道机动大小、空间方向等参数。
