人教A版高中数学新旧教材“概率”的比较研究

李杰民 廖运章

【摘 要】 与实验教材相比，人教A版高中数学新教材中概率内容的改编力度很大：有新增有删减，有强调有淡化，有顺序调整，有概念重构. 新教材明晰了概率论的研究对象与研究方法，降低了概率起始教学的难度. 概率教学需要理解“样本空间”的基础地位与构建原则，重视“随机事件”概念及其符号化的教学，尽量采用计算机软件开展随机模拟活动.

【关键词】 人教版高中数学教材;概率;样本空间;随机事件;事件的相互独立性

依据《普通高中数学课程标准（2017年版）》（以下简称《新课标》）[1]编写的人教版高中数学新教材即将在全国多地投入使用，这是一套核心素养导向的高中数学新教材，关于新教材的解读与研究成为当前的重要任务与研究热点. 文[2]从整体上介绍了人教A版高中数学新教材在编写理念、教材结构、知识内容编排、例题和习题设置五个方面的特色，提出了教材的使用建议. 笔者认真研读了上述教材，发现“概率”部分除了具有文[2]所指出的特色以外，还具有改编力度大，知识结构更加符合学科逻辑的显著特点. 特别是，新教材给出了与旧教材完全不同的“随机事件”的定义，将“频率与概率”提升为单独一节，将“事件的相互独立性”由旧教材选修提前到新教材必修. 笔者认为，这三个主要变化带动了概率章节内容的一系列调整，应当重点关注，认真研究.

为了全面、准确地理解新教材中“概率”内容的编写情况及其理念，本文首先给出新旧教材“概率”章节教学内容的比较，梳理新教材出现的深刻变化;然后，围绕上述三个主要变化，对变化的原因、内容之间的逻辑关系与教学中需要重点关注的内容进一步解读;最后，给出教学建议.1 新旧教材“概率”内容的比较

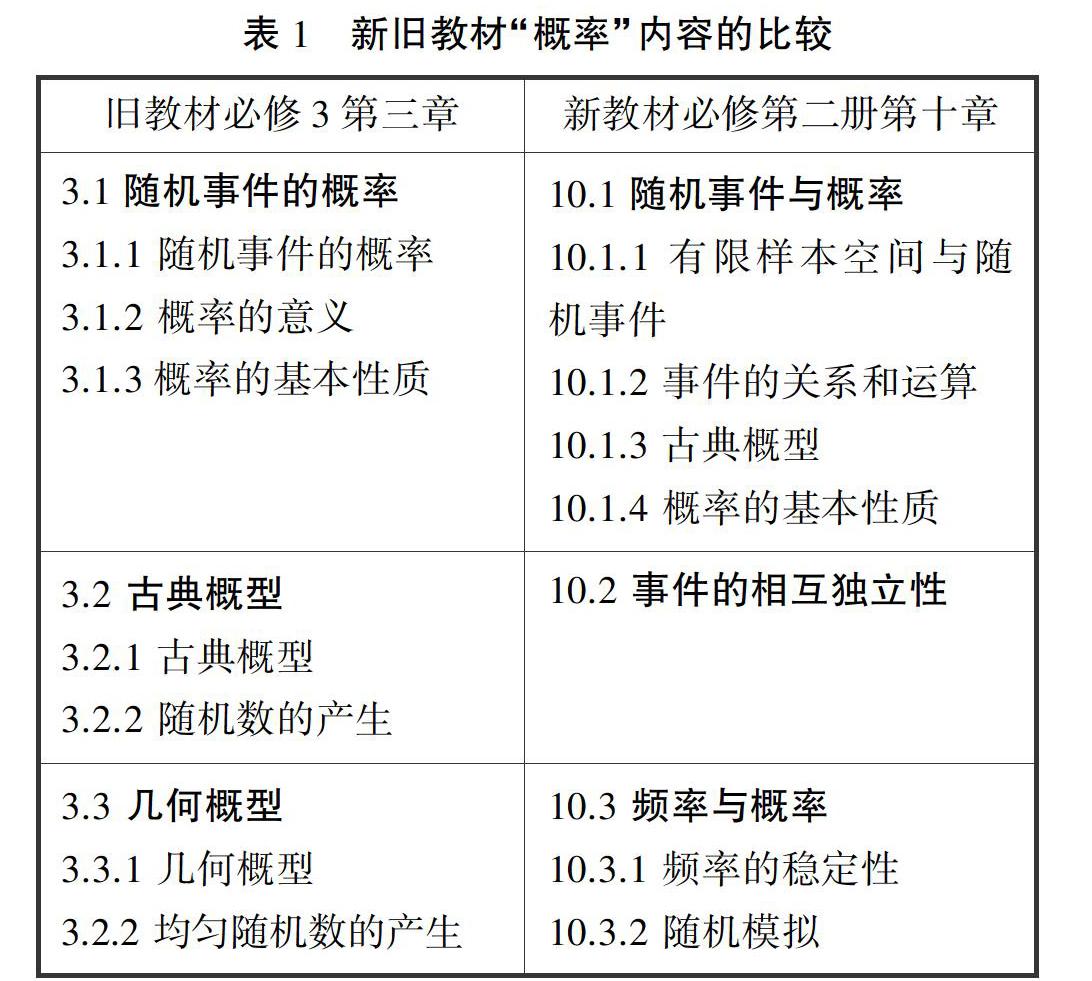
为了对“概率”内容的改写情况有一个清晰的认识，首先对新教材必修第二册的第十章“概率”与旧教材必修3的第三章“概率”作一个比较，如表1所示. 可以看出，新教材必修第二册的第十章“概率”分为三节：“10.1 随机事件与概率”“10.2 事件的相互独立性”“10.3 频率与概率”;旧教材必修3的第三章“概率”也分为三节：“3.1 随机事件的概率”“3.2 古典概型”“3.3 几何概型”. 虽然新旧教材都是分为三节，但从三节的标题对比即可以看出，教学重点发生了明显的改变.

具体而言，主要变化是：其一，旧教材“3.3几何概型”在新教材中被删除，新教材增加了“有限样本空间”;旧教材“3.1.2 概率的意义”被删除，但保留了其中的“孟德尔遗传规律的试验与发现”，改编调整到章尾处的“阅读与思考”之中. 其二，旧教材“3.2 古典概型”“降级”为新教材中的“10.1.3 古典概型”，新教材的目录部分不再有“古典概型”，不难理解，这是一种淡化之意;而“隐藏”在旧教材“3.1.1 随机事件的概率”中的“频率与概率”提升为新教材“10.3 频率与概率”，单独列为一节， 可以理解为凸显其难度或重要性之意，但也并非简单的强调，笔者认为，由于频率的稳定性涉及“依概率收敛”理论，内容抽象，难度较大，中学阶段并不介绍概率论中的收敛理论，因此，单独列出考虑到了该内容的难度、所需学时以及内容的独特性. 其三，“事件的相互独立性”由旧教材选修23的“2.2二项分布及其应用”的子目录“2.2.2 事件的相互独立性”提前到新教材必修，这是一个跨度最大的教学顺序调整，提前教学并且“升级”为单独一节“10.2 事件的相互独立性”. 另外，原本分散在“3.2 古典概型”与“3.3几何概型”中的“随机数的产生”合并调整到新教材“10.3 频率与概率”的子目录“10.3.2 随机模拟”.

此外，还有一个容易被忽视但特别重要的细节：旧教材“3.1 随机事件的概率”与新教材“10.1 随机事件与概率”的标题存在差异，新教材明确区分了“随机事件”与“随机事件的概率”，对“随机事件”概念进行了重构. 换言之，新教材概率起始教学内容发生了深刻的改变.

2 新教材概率教学需要重点关注的内容

通过上述比较可知，概率内容改动力度很大，既有新增也有删减，既有“升级”强调也有“降级”淡化，还有教学顺序的前后调整，等等. 需要指出的是，这些变化具有很强的逻辑关联性，并非简单的知识重组. 另外，还有概念的重构，比如，改写了“随机事件”的定义，这需要进一步研究具体内容才能了解重构的细节与原因. 为此，以下对新教材概率教学需要重点关注的内容做进一步的解读.

2.1 有限样本空间与随机事件

新教材“章首语”首先介绍“隨机现象”以及概率论的研究对象，然后，“10.1.1 有限样本空间与随机事件”指出概率论研究随机现象的方法——随机试验，逐步得到“样本点”“样本空间”“有限样本空间”等概念，最后给出“随机事件”的定义，将“随机事件”定义为“样本空间的子集”. 换言之，新教材对“随机事件”概念进行了重构，有两点需要特别注意.

其一，新教材“随机事件”的定义与旧教材完全不同. 该定义的优点在于：首先，与日常生活中的同名概念划清了界限，有效区分了生活中的“随机事件”与数学世界中的“随机事件”，避免了旧教材以“在一定条件下，可能发生也可能不发生的事件称为随机事件”这样一个不严谨的定义所带来的教学上的混乱. 其次，保证了“随机事件”定义的科学性. 严格地说，“随机事件是样本空间的子集”是一个真命题，但“样本空间的子集是随机事件”是一个假命题，原因在于：对于无限样本空间而言，可能存在不可测子集，即并非每一个子集都可以称为随机事件，但如果限定为“有限样本空间”，则不会出现上述困惑. 因此，“有限样本空间”保证了“随机事件”定义的科学性，同时，降低了高中“概率”起始教学的难度，与新课标界定的“必修”课程的定位相符. 第三，接近大学阶段的定义，有利于高中与大学阶段的衔接.

其二，新教材明晰了概率论的研究对象与研究方法. 新教材从“章首语”到“10.1随机事件与概率”，花费大量篇幅推出概率论的基本概念——随机事件，并介绍随机事件的关系和运算、“古典概型”情形下的概率计算以及概率的性质，详细展示了概率论的研究对象与研究方法，以及通过“随机试验”将研究对象转化为“随机事件”的技术路线，对于增进师生对概率论的理解非常有益. 比较新旧教材的“章小结”的“知识结构图”可知，新教材“概率”的知识结构更加清晰，更加符合概率学科的逻辑结构，明晰了概率论的研究对象与研究方法，有利于师生对概率内容的理解与整体把握.

2.2 事件的相互独立性

旧教材选修23“2.2.2 事件的相互独立性”的编写情况：以“三名同学有放回地抽取奖券”为引例，事件A表示“第一名同学没有抽到中奖奖券”，事件B表示“最后一名同学抽到中奖奖券”，凭常识可知P（BA）=P（B），结合乘法定理P（AB）=P（A）P（BA），得到P（AB）=P（A）P（B），由此引出事件A与事件B相互独立的定义.

新教材必修第二册“10.2 事件的相互独立性”编写情况：首先，从两个随机试验（抛掷硬币试验，有放回摸球试验）为探究载体，分别计算P（A）、P（B）、P（AB），引导学生发现两个试验的共性，即P（AB）=P（A）P（B），从而归纳出“独立性”概念. 此外，例题增加到3个，且3个例题代表不同的使命：例1是一个反例，告诫初学者“独立性”不常有，使用需谨慎. 例2、例3给出了使用独立性解题的条件，其中例2本身沒有说明“独立性”，“独立性”条件隐含在事件的实际意义中;例3声明“互不影响”，直接告知“独立性”条件.

需要特别提醒的是，旧教材将“事件的相互独立性”作为“条件概率”的后续，作为“乘法定理”的特殊情形，采用的是演绎推理的形式. 新教材重构了“事件的相互独立性”，通过归纳推理方式获得概念，并且，通过正反例结合深化对概念的理解，改写力度很大. 从现实课堂教学以及公开的教学视频与教学论文可知，许多教师受到传统教材（包括大学教材）编写顺序的影响，机械套用“最近发展区”理论，认为从“条件概率”入手才能深刻地理解“独立性”. 新教材将“事件的相互独立性”提前到必修课程，此时尚未学习“条件概率”，适应旧教材的教学设计必须改变[3].

2.3 频率与概率

频率的稳定性、频率稳定于概率、频率稳定于概率为获取随机事件的概率提供了一种估算方法，这些重要而且具有难度的知识点原本内嵌于旧教材“3.1.1 随机事件的概率”之中，新教材将这些内容改写并“升级”为单独一节“10.3 频率与概率”，其中“10.3.1 频率的稳定性”通过“探究”“试验”“折线图”等方法归纳出“频率的稳定性”概念;“10.3.2 随机模拟”介绍了“用频率估计概率”的计算机模拟方法——采用电子表格软件模拟大量重复试验.

可见，新教材明确区分了概率的理论计算与估算，理论计算放在前两节，估算方法放在最后一节，编写思路更加清晰，给师生的教与学带来了便利.3 新教材概率内容的教学建议

为了理解好、使用好、发挥好新教材的价值，走出旧教材造成的思维定势，在对新旧教材内容的比较、以及新教材主要内容解读的基础上，给出以下教学建议，供高中数学同仁教学参考.

3.1 理解“样本空间”的基础地位与构建原则

新教材从“章首语”到“10.1.1 有限样本空间与随机事件”“10.1.2 事件的关系和运算”花费了大量的篇幅介绍“随机事件”，凸显了“随机事件”作为概率论的基础概念的重要性. 因为“随机事件”是“样本空间的子集”，所以，构建合适的样本空间是表达和刻画“随机事件”的前提. 因此，教师研读教材，不仅要熟悉知识点，还要理解“样本空间”在概率论中的基础地位与构建原则.

比如，因为“有限样本空间”的限制，“几何概型”被删除也就成为必然. 从多年的教学实践来看，“几何概型”教学存在许多误区甚至错误，“几何概型”中的“等可能性”与“古典概型”中的“等可能性”存在质的区别，中学阶段很难解释清楚，因此，删除“几何概型”也是出于难度的考虑.

又如，“10.1.1 有限样本空间与随机事件”出现了4个要求写出样本空间的例题，由于都是有限样本空间，初学者很容易产生错觉：其一，写出样本空间是一件容易的事情;其二，写出样本空间后，随机事件可以一一列出，因此写出随机事件也是一件容易的事情. 然而，在复杂随机现象的研究中，写出样本空间往往是一件很困难的事情，即使在大学或中学的概率教学中，也存在一定的困难. 困难在于：其一，难以写出甚至无法写出. 比如，学习选择性必修课程第三册第七章中的“全概率公式”时将会发现，涉及“全概率公式”的问题往往是先写出“完备事件组”，即给出样本空间的一个“划分”，间接确定样本空间;学习“随机变量”后将会发现，“随机变量”建立起“样本空间”到“欧式空间”的一个映射，有关概率计算的问题转移到“欧式空间”（中学阶段主要是直线或平面），此时已经看不到“样本空间”，但要真正理解通过“随机变量”表达的“随机事件”，依然依赖于作为原像集的“样本空间”. 其二，即使是较为简单的问题，容易写出样本空间，也需要考虑样本空间的创建原则. 一般而言，样本点尽量简单，或者说，基本事件尽量简单，不能再分解. 不能“再分解”的标准由问题背景决定. 正如史宁中先生指出：样本空间的创建与问题背景有关，与问题本身无关[4]. 因此，教师应理解“样本空间”的构建原则，不可随意构建样本空间，否则，将给教学带来困扰.

另外，教师要引导学生感受样本空间的动态性与复杂性. 比如，新教材“10.1.1 有限样本空间与随机事件”中的4个例题的样本点分别是英文字母、自然数、2维的点、3维的点. 教师要做好示范，引导初学者认认真真写好样本空间，为研究后续复杂的概率问题奠定基础.3.2 重视“随机事件”概念及其符号化的教学

“事件”与“事件的概率”是概率论中两个最基本的概念[5]. 换言之，两者都很重要，两个概念都要清楚的界定，这是概率论研究者的常识，新教材的编写为此付出了努力. 具体表现在：其一，旧教材的目录与子标题均没有出现“随机事件”，新教材则花费大量的篇幅重构“随机事件”，凸显“随机事件”概念的重要性，避免了旧教材不讲“随机试验”直接进入“随机事件的概率”而造成的教学上的混乱[6]. 其二，“事件的概率”的准确定义要在公理化概率论中才能严格的表达，旧教材第一节“3.1.1 随机事件的概率”直奔“事件的概率”，新教材的目录与子标题均没有出现“随机事件的概率”，直到“10.1.3古典概型”才出现“事件的概率”的字样，但并非定义. 总之，新教材给出了和大学阶段接近的“随机事件”的定义，但对于中学阶段无法严格定义的“事件的概率”，则采取了“低调”的处理方式. 换言之，新教材传递了需要重视“随机事件”概念教学的信号.

关于随机事件概率的计算，除了基本事件的概率比较容易获得，一般而言，计算较为复杂的随机事件的概率，需要借助事件的关系和运算，以及概率的性质. 因此，随机事件的符号化特别重要，需要引起教师的重视，耐心做好示范教学. 事件符号化以后，把待求概率的随机事件转化为基本事件或者容易求出概率的事件的数学表达式，再利用概率的性质，计算出待求随机事件的概率.

比如，“10.2 事件的相互独立性”中的例3，事件A=“两轮活动星队猜对三个成语”，事件A的概率难以直接计算，但可以表示为：A=A1B2∪A2B1，而事件A1、A2、B1、B2的概率的计算相对简单，利用事件的关系与性质得到P（A）=P（A1）P（B2）+P（A2）P（B1），从而获得较为复杂的事件A的概率.

3.3 重视概率的估算方法的教学，尽量采用计算机软件开展随机模拟活动

概率的计算与估算是研究随机事件发生可能性大小的两种不同的方法. 新教材明确区分了两者的差异，将旧教材“3.1.1 随机事件的概率”之中的一个知识点“用频率估计概率”提升为单独一节“10.3 频率与概率”，明显表达了需要引起重视的信号. 笔者认为，新教材将“频率与概率”单独列为一节，一是有利于分解教学难点，二是通过“探究”“试验”“折线图”等方法体验“频率的稳定性”，是中学生喜闻乐见的有利于化解抽象概念的數学探究活动，有利于调动学生的学习兴趣与课堂参与. 但采用电子表格软件模拟大量重复试验的活动往往需要占用较多的教学时间，对不熟悉电子表格的概率统计功能的教师而言，还需要花一些时间学习如何使用. 但是，随机数学具有不同于确定性数学的独特性，随机模拟不仅有利于调动学生的学习兴趣，也是促进概率与统计融通的技术手段. 因此，教师需要转变观念，与时俱进，为发展学科核心素养而教，尽量采用计算机软件开展随机模拟活动，不要因为测评难以考查或者因为占用较多时间而忽视该内容的教学.

参考文献

[1] 中华人民共和国教育部. 普通高中数学课程标准（2017年版）[M]. 北京：人民教育出版社，2018.

[2] 邵光华，张妍. 人教A版高中数学新教材特色分析与适用建议[J]. 课程·教材·教法，2019，39（12）：109114.

[3] 李杰民. 事件的相互独立性的重新认识与教学建议[J]. 中国数学教育（高中版），2020，（07/08）：2833.

[4] 史宁中. 数形结合与数学模型——高中数学教学中的核心问题[M]. 北京：高等教育出版社，2018：8990.

[5] 戴朝寿. 概率论简明教程（第二版）[M]. 北京：高等教育出版社，2016：4.

[6] 何小亚. 高中概率模型学与教中的问题和对策[J]. 数学教育学报，2017，26（01）：3740.

作者简介

李杰民（1973—），男，湖南平江人，岭南师范学院讲师，博士研究生，主要从事数学教育研究，发表论文10余篇.

廖运章（1964—），男，广西罗城人，广州大学教授，博士生导师，主要从事数学教育研究.