Propagation of oblique water waves by an asymmetric trench in the presence of surface tension

Anjan Sasmal,Soumen De

Department of Applied Mathematics,University of Calcutta,92,A.P.C.Road,Kolkata 700009,India

Abstract An analysis is presented for the propagation of oblique water waves passing through an asymmetric submarine trench in presence of surface tension at the free surface.Reflection and transmission coefficients are evaluated applying appropriate multi-term Galerkin approximation technique in which the basis functions are chosen in terms of Gegenbauer polynomial of order 1/ 6 with suitable weights.The energy identity relation is derived by employing Green’s integral theorem in the fluid region of the problem.Reflection and transmission coefficients are represented graphically against wave numbers in many figures by varying several parameters.The correctness of the present method is confirmed by comparing the results available in the literature.The effect of surface tension on water wave scattering is studied by analyzing the reflection and transmission coeffciients for a set of parameters.It can be observed that surface tension plays a qualitatively relevant role in the present study.

Keywords: Water wave scattering;Surface tension;Asymmetric trench;Gegenbauer polynomial of order 1/ 6;Galerkin approximation;Reflection and transmission coefficients.

1.Introduction

A class of problems involving the propagation of water waves by variable geometrical shapes of infinite or finite depth water has attracted much attention in recent years.There have been many investigations of the problems of scattering of water wave over various depth geometries (Kreisel[1],Mei and Black [2],Lassiter [3],Lee and Ayer [4],Miles[5],Kirby and Dalrymple [6],Jung et al.[7],Xie et al.[8],Liu et al.[9],Chakraborty and Mandal [10,11]).Roy et al.[12]investigated the problem of propagation of obliquely incident water waves over an asymmetric rectangular trench applying the multiterm Galerkin approximations involving ultraspherical Gegenbauer polynomials for solving the integral equations arising in the mathematical analysis.The problem of oblique wave scattering by an asymmetric trench beneath a large floating ice sheet was studied by Paul et al.[13]applying the multiterm Galerkin approximations.Recently,Das et al.[14]studied the problem of oblique scattering of surface waves by a thick partially immersed rectangular barrier or a thick submerged rectangular barrier extending infinitely downwards in deep water using multi-term Galerkin approximation involving simple polynomials as basis functions multiplied by appropriate weight functions.

A number of notable works have been accomplished with the effect of surface tension at the free surface in water wave problems involving obstacles.Many aspects of wave interaction with obstacles in presence of surface tension at free surface have been studied by Evans [15],Evans[16],Rhodes-Robinson [17],Rhodes-Robinson [18],Rhodes-Robinson [19],Harter et al.[20].Very recently,the influence of surface tension of oblique water wave scattering by a rectangular symmetric trench is investigated by Sasmal et al.[21]applying the multiterm Galerkin approximations involving ultraspherical Gegenbauer polynomials.

Fig.1.Definition diagram for asymmetric trench.

Having studied the above works and realizing that till now no one else has attempted the problem of propagation of oblique water wave by an asymmetric trench in the presence of surface tension at the free surface.The effect of surface tension is included since the amplitude and the frequency of the wave depends on both the surface tension and gravity.Another important reason for including surface tension is that in the absence of surface tension the transient motion initiated by an impulsive start is singular,but when the effect of surface tension is taken into account this singularity is removed as mentioned by Hocking and Mahdmina [22].

In the present study,we have investigated the problem of oblique water wave scattering by an asymmetric trench with the effect of surface tension at the free surface.The fluid domain is divided into three regions with uniform but unequal depths.To solve the problem the potential function is reduced to linear integral equations using the eigenfunction expansions along with the Havelock inversion formula followed by a matching process.Using the multiterm Galerkin approximations the integral equations are approximated involving ultraspherical Gegenbauer polynomials.Once the integral equations are solved,the reflection and transmission coefficients can be obtained.Applying Green’s integral theorem,energy identity relation is derived in the fluid region of the problem.Numerical estimates for the reflection and transmission coefficients are obtained for various values of different parameters involved in the problem.The effects of the surface tension and the depth of each side of the asymmetric trench,as well as the width of the asymmetric trench,are investigated graphically.The effect of oblique incidence of the water wave is also taken into account to analyze the physical quantities.

2.Physical problem and mathematical formulation

In the present context,the BVP considered arises in the broad area of fluid-structure interaction,where the fluid is assumed to be inviscid and incompressible and the fluid motion is irrotational and simple harmonic in time.A coordinate system is established with the positive y-axis is taken vertically downward and x-axis is horizontal as shown in the definition sketch in Fig.1.The rectangular domain of asymmetric trench of depthd3and width 2dis connected with two channels of constant,but different depths,d1andd2.For the convenience study,the fluid region divided into three subregions,namely Region-I ≡(-∞＜x＜-d,0＜y＜d1);Region-II ≡(-d＜x＜d,0＜y＜d3)and Region-III ≡(d＜x＜ ∞,0 ＜y＜d2),respectively.We wish to investigate the diffraction of a plane surface wave incident from infinity in Region-I with an angleθon the trench.Assuming linear theory,the time harmonic motions of the fluid are described by the velocity potentialΦinc(x,y,z,t)=withis the real positive root ofk(1+Mk2)tanhkd1=Kwherebeing the acceleration due to gravity andωis the angular frequency of incident wave andτis the coefficient of surface tension at the free surface of the ocean andρis the density of fluid.According to the Snell’s law for refraction across discontinuities in the water depth,the projectionνof incident wave number satisfieswhereare the real positive roots of the transcendental equationk(1+Mk2)tanhkdj=K(j=2,3).The velocity potentialφ(x,y)satisfies the governing partial differential equation is given by

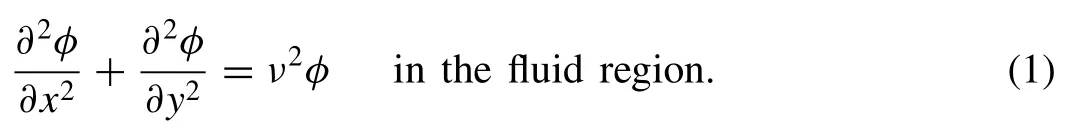
The free surface boundary condition in presence of surface tension is given by

the bottom boundary conditions,

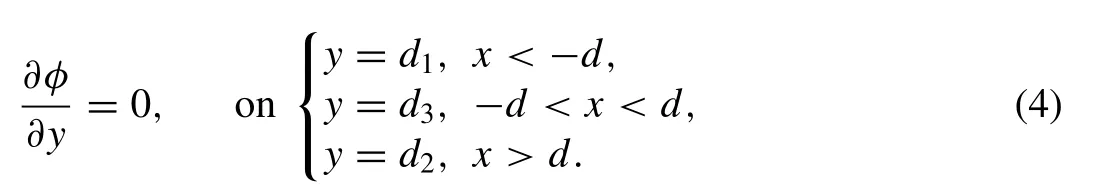
The velocity potential is bounded everywhere in the f luid region except at the submerged sharp edges(-d,d1)and(d,d2)of the trench.The edge condition may be w ritten as

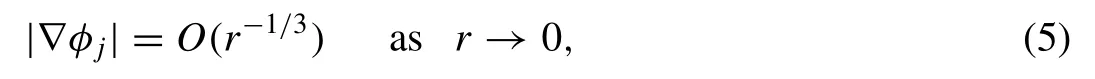
where ∇=(∂/∂x,∂/∂y)andris the distance from the edges of the trench.The conditions at inf inity are given by

whereRandTare the unknown complex ref lection and transm ission coeff icients to be determ ined and=

In addition to these boundary conditions,we must require the horizontal velocity and the potential be continuous at the common boundary of the regions.These matching conditions are given by

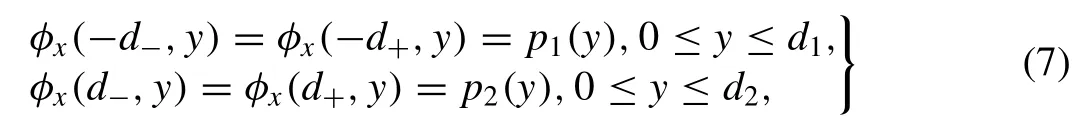
and

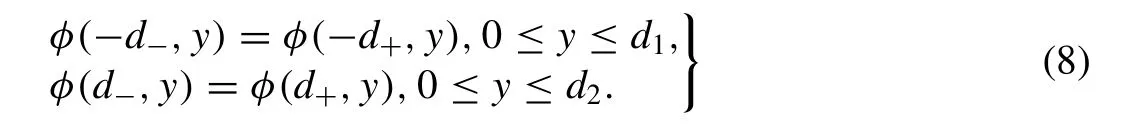
3.M ethod of solution

Using the Havelock’s expansion formula,the velocity potentialsφ(x,y)for each of the subregions are given by

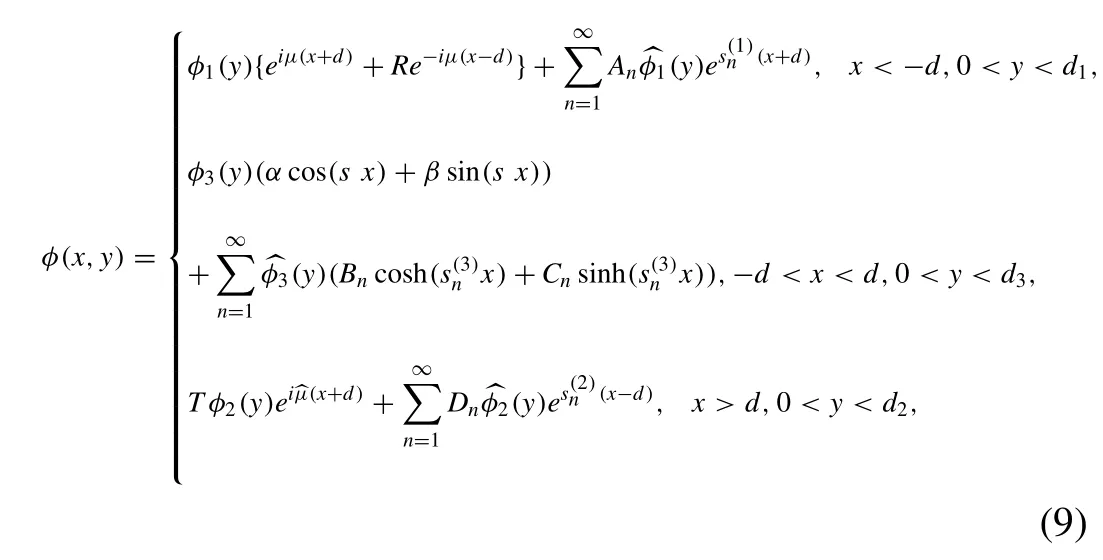
Using the expressions for velocity potentials from Eq.(9) into continuity condition across the gap in Eq.(7)and followed by the Havelock’s inversion formula,we obtain the unknown constants as

Moreover,continuity condition ofφ(x,y)atx=±dgiven in Eq.(8) leads to a set of integral equations which are given by

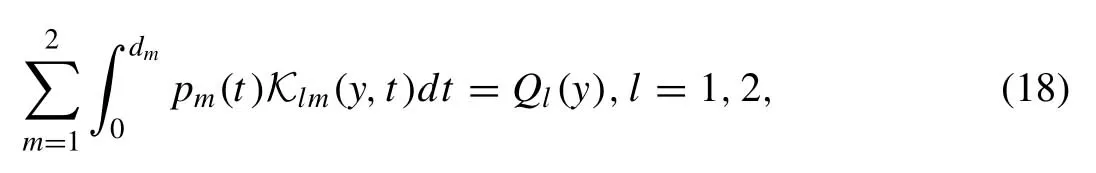
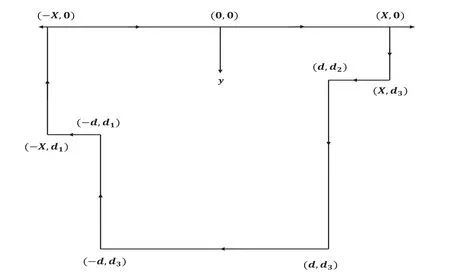
Fig.2.Contour for the structure.

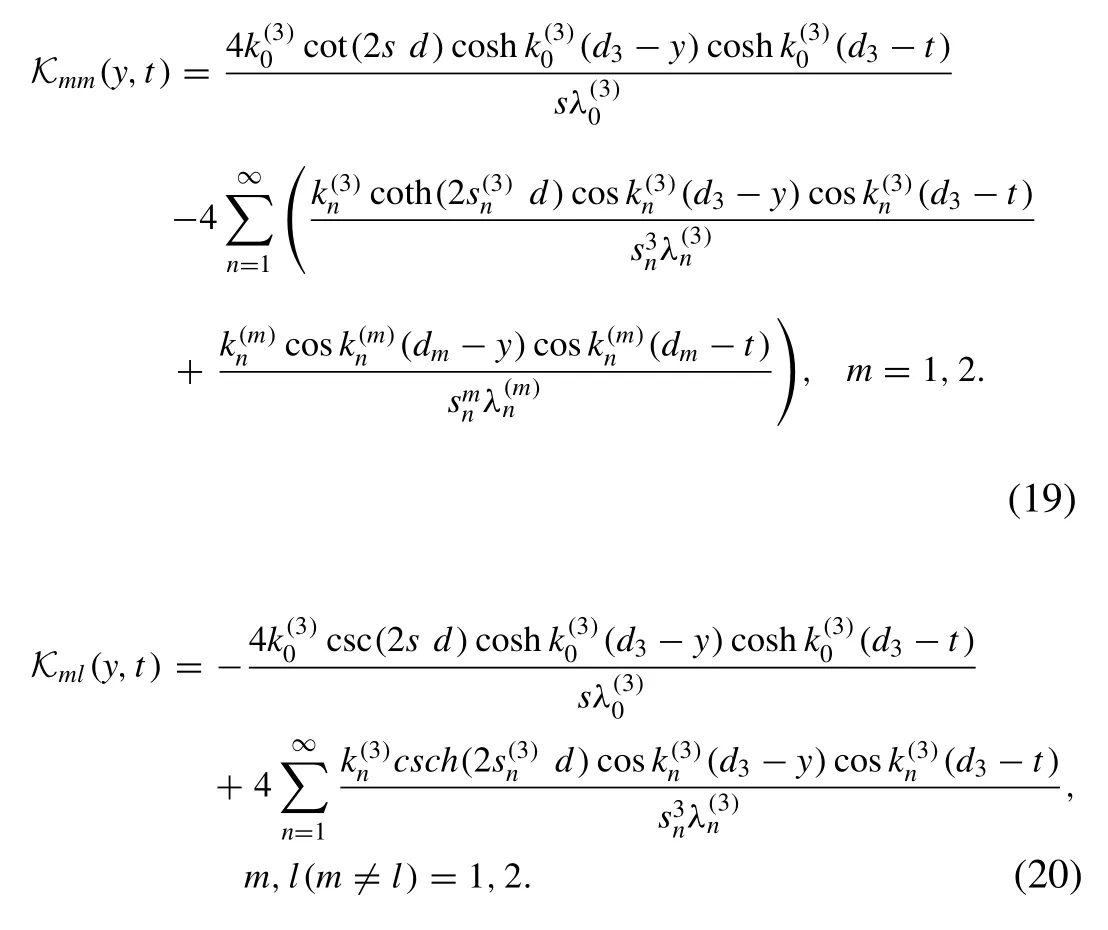
Let us assumepm(t)as

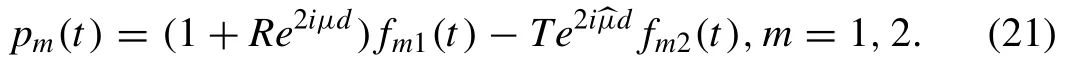
After using the expressions ofpm(t)from Eq.(21),the equations in (18) can be reduce as

whereδl jis the Kronecker delta symbol.

Substituting the expression from Eq.(21) into the Eqs.(10) and (16),then these equations can be written in the matrix notation as

where

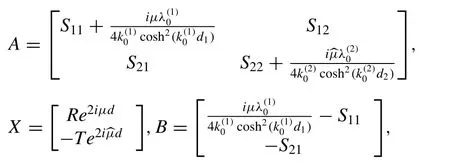
Once the unknown functionsfml(t)(m,l=1,2.)are determine after solving the system of equation in (22) we can computedRandT.

4.The multi-term Galerkin approximation technique

A (N+1)-term Galerkin approximation technique is used to determine the solution of the integral equations in (22).Since the functionsfml(y)(m,l=1,2)are connected to the horizontal velocitiespm(y),then we take the(N+1)-term expansion of the form:

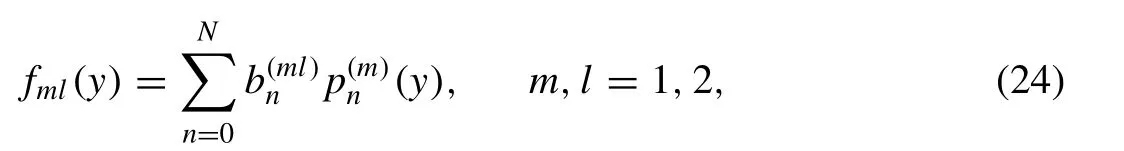
whereare the suitably chosen basis functions.

To chose the basis functions in Eq.(24) we consider the effect of surface tension at free surface and the edge condition at(-d,d1)and(d,d2).Thus,(y)≡G(y);m=1,2,satisfies

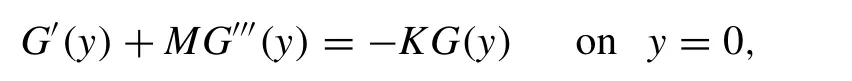
and

A basis function in terms of ultra-spherical Gegenbauer polynomial of orderwith suitable weights (c.f.Kanoria et al.[23];Evans and Fernyhough [24]) can be given byin 0＜y＜dm,

with

Substituting the expressions from Eq.(24) into the integral equations in (22),then multiplying themth integral equation in (22) by(y)and integrating over(0,dm),we obtained the following system of equations as

where

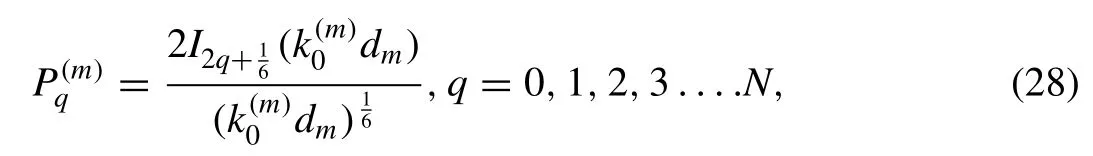
whereJn(x)andIn(x)are Bessel functions of first kind and modified Bessel functions of first kind of ordern,respectively.

After solving the system of equations in (25),we obtainand henceSml,m,l=1,2,are found from

5.Energy balance relation

In this section,energy balance relation is derived using Green’s integral theorem to the functionφ(x,y)and its complex conjugatewhich yields

where

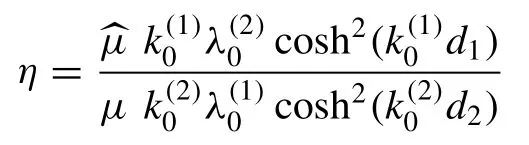
6.Numerical results

In this section,the effect of the asymmetric trench in the presence of surface tension at the free surface on the propagation of oblique waves can be demonstrated by computing reflection and transmission coefficients.These quantities are connected by a relation which obtains theoretically provides a numerical check for the results obtained through numerical computation(see Eq.(31)).To construct a solution,it is first necessary to truncate infinite series in the Eq.(25) involvingto a finite number of terms.

6.1.Convergence of results

Accuracy of the numerical method presented here depends highly on the truncation size of infinite series in expansion of the velocity potential and the number of terms(i.e.N+1)considered in the Galerkin expression which are explained in this section.A four-figure accuracy is achieved by taking 30 terms in each series.A representative set of these numerical estimates for|R|are tabulated in Table1 taking some particular values ofM/d12=1,θ=45o,d/d1=5,d2/d1=1.2,d3/d1=2=0.2,0.4,0.6,0.8,1.0,1.2,1.4,1.6,1.8,2,andN=0,1,2,3,4,5.It is observed from this table that the numerical estimates for|R|converge very rapidly withN,and forN=4 or 5,an accuracy up to four figures is achieved.The numerical study for|R|and|T|are carried out takingN=4 for different values of depth of the trench,trench width,surface tension,angle of incidence.

Table1 Values of|R|,for fixed values of

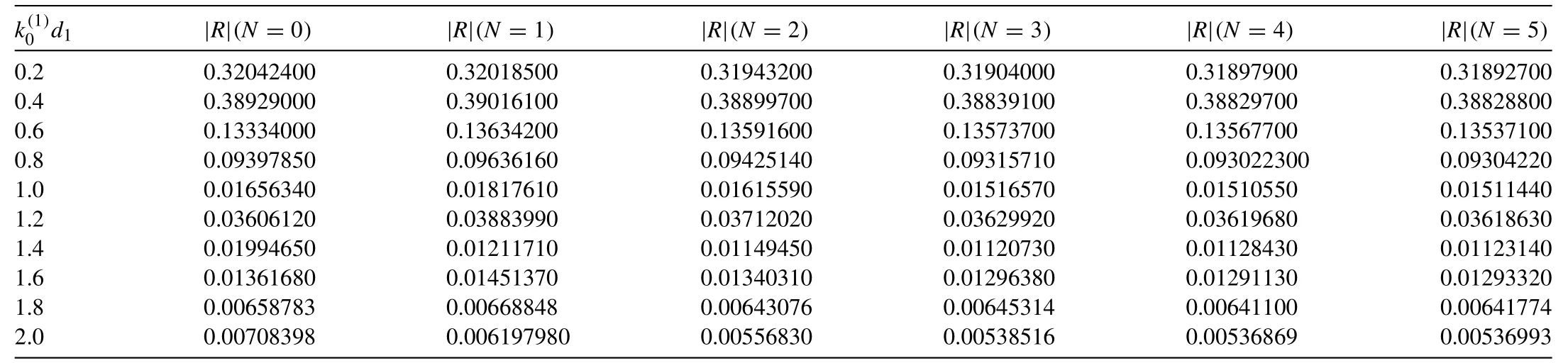
Table1 Values of|R|,for fixed values of

k (1)0 d 1|R|(N=0)|R|(N=1)|R|(N=2)|R|(N=3)|R|(N=4)|R|(N=5)0.2 0.32042400 0.32018500 0.31943200 0.31904000 0.31897900 0.31892700 0.4 0.38929000 0.39016100 0.38899700 0.38839100 0.38829700 0.38828800 0.6 0.13334000 0.13634200 0.13591600 0.13573700 0.13567700 0.13537100 0.8 0.09397850 0.09636160 0.09425140 0.09315710 0.093022300 0.09304220 1.0 0.01656340 0.01817610 0.01615590 0.01516570 0.01510550 0.01511440 1.2 0.03606120 0.03883990 0.03712020 0.03629920 0.03619680 0.03618630 1.4 0.01994650 0.01211710 0.01149450 0.01120730 0.01128430 0.01123140 1.6 0.01361680 0.01451370 0.01340310 0.01296380 0.01291130 0.01293320 1.8 0.00658783 0.00668848 0.00643076 0.00645314 0.00641100 0.00641774 2.0 0.00708398 0.006197980 0.00556830 0.00538516 0.00536869 0.00536993

Table2 Values of|R|,|T|,η and|R|2+η|T|2 for fixed values of

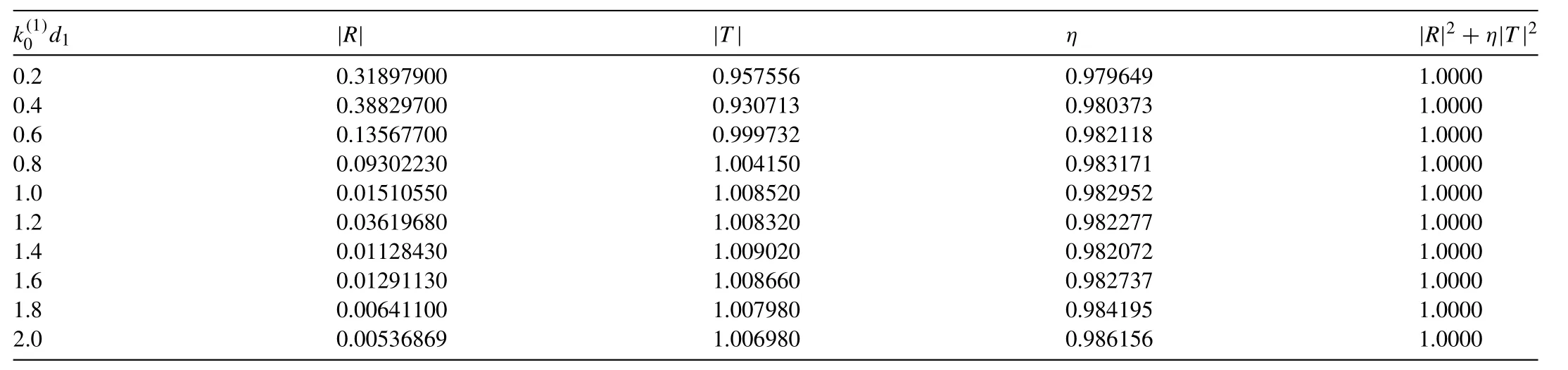
Table2 Values of|R|,|T|,η and|R|2+η|T|2 for fixed values of

k (1)0 d 1|R||T|η|R|2+η|T|2 0.2 0.31897900 0.957556 0.979649 1.0000 0.4 0.38829700 0.930713 0.980373 1.0000 0.6 0.13567700 0.999732 0.982118 1.0000 0.8 0.09302230 1.004150 0.983171 1.0000 1.0 0.01510550 1.008520 0.982952 1.0000 1.2 0.03619680 1.008320 0.982277 1.0000 1.4 0.01128430 1.009020 0.982072 1.0000 1.6 0.01291130 1.008660 0.982737 1.0000 1.8 0.00641100 1.007980 0.984195 1.0000 2.0 0.00536869 1.006980 0.986156 1.0000

6.2.Validation of results

6.2.1.Validationthroughenergyidentity

The reflection and transmission coefficients corresponding to the wave scattering by an asymmetric trench in the presence of surface tension satisfying the energy balance relation given in Eq.(31) are shown in the Table2.This gives a partial check on the correctness of the numerical results obtained here.

6.2.2.Comparisonwithpreviousresults

To verify the trend of the present results,the comparison is made with the corresponding cases available in the literature.By takingM=0 in Eq.(2),the boundary condition of the problem reduces to free surface condition without the effect of surface tension was studied by Kirby and Dalrymple [6]and Roy et al.[12].

Our results are compared in Fig.3 to points taken from Fig.5 of Kirby and Dalrmple [6]for the case of a symmetric trench,for the geometry0,θ=45o.

Fig.3.|T|against 45 o.

The curves of Fig.3 shows the good agreement of the corresponding curves of Fig 5 plotted by Kirby and Dalrymple[6].

A comparison with the results of Lee and Ayer [4]for the case of a symmetric trench with normal incident wave is shown in Fig.4,where|R|is plotted againstrather thanfor the geometry0,θ=0o.From Fig.4,it is clear that present results agree closely with the result plotted in Fig.2 by Lee and Ayer [4].

Fig.4.|R|against for =2.0,=1.0,=2.5,=0,θ=0o.

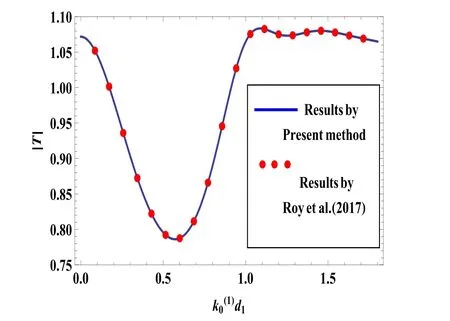
Fig.5.|T|againstfor=2.5,=1.5,=3.5,=0,θ=45o.

Another comparison is made with the work of Kirby and Dalrymple [6]for the case of asymmetric trench.In Fig.6,transmission coefficient is depicted againstfor fixedand for different values ofIt is observed that the two curves in this figure coincide with the curves(a)and(c)of Fig.8 of Kirby and Dalrymple [6].

6.3.Results

In Figs.7 and 8,the reflection and transmission coefficients are plotted againstfor various values of angle of incidence with fixed values ofrespectively.It is observed that reflection coefficient increases as the angle of incident increases while|T|has an opposite pattern.Fig.8 reveals that,the amplitude of transmission coefficient is high atθ=60ofor smaller values of

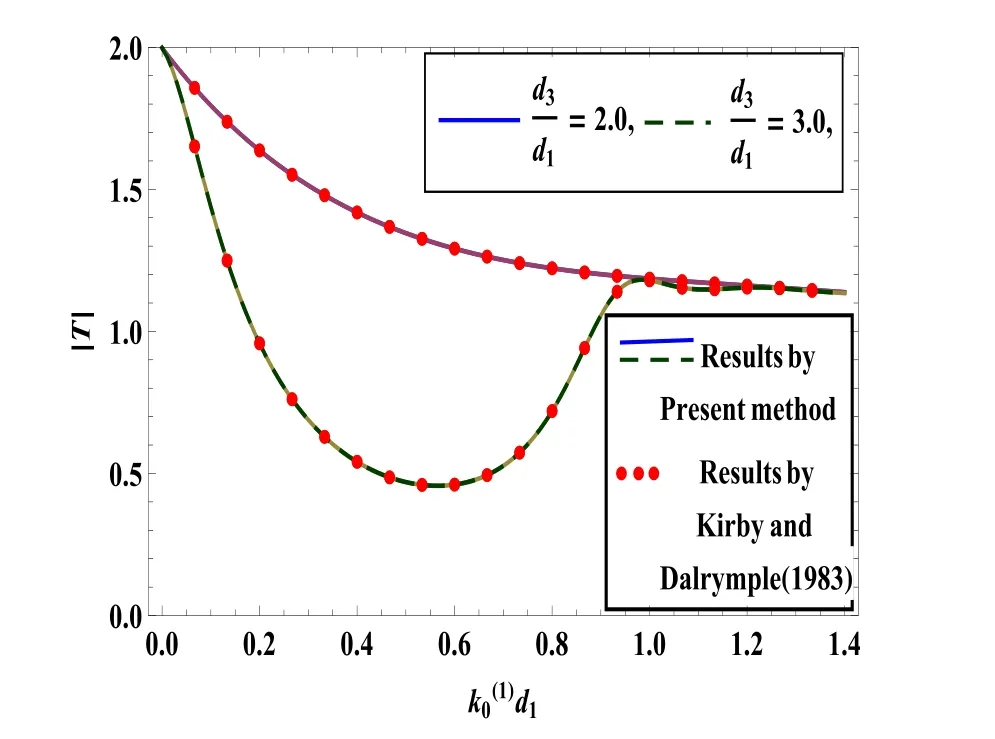
Fig.6.|T|against for=2.0,=5.0,=0,θ=45 o.

Fig.7.|R|for different values of angles in presence of surface tension.

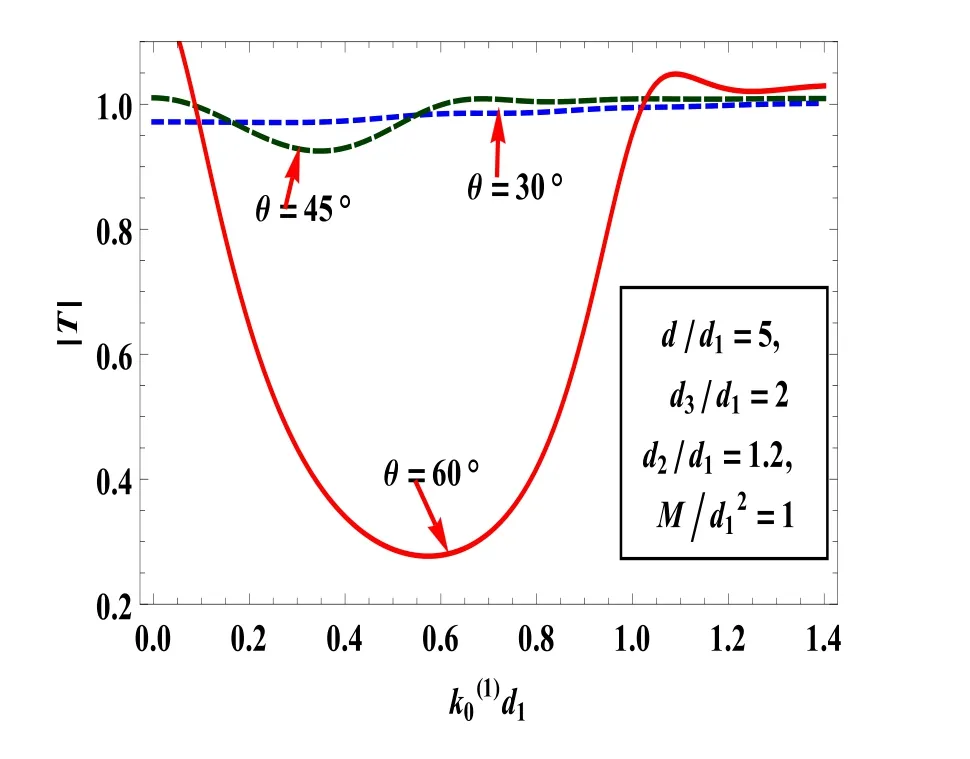
Fig.8.|T|for different values of angles in presence of surface tension.

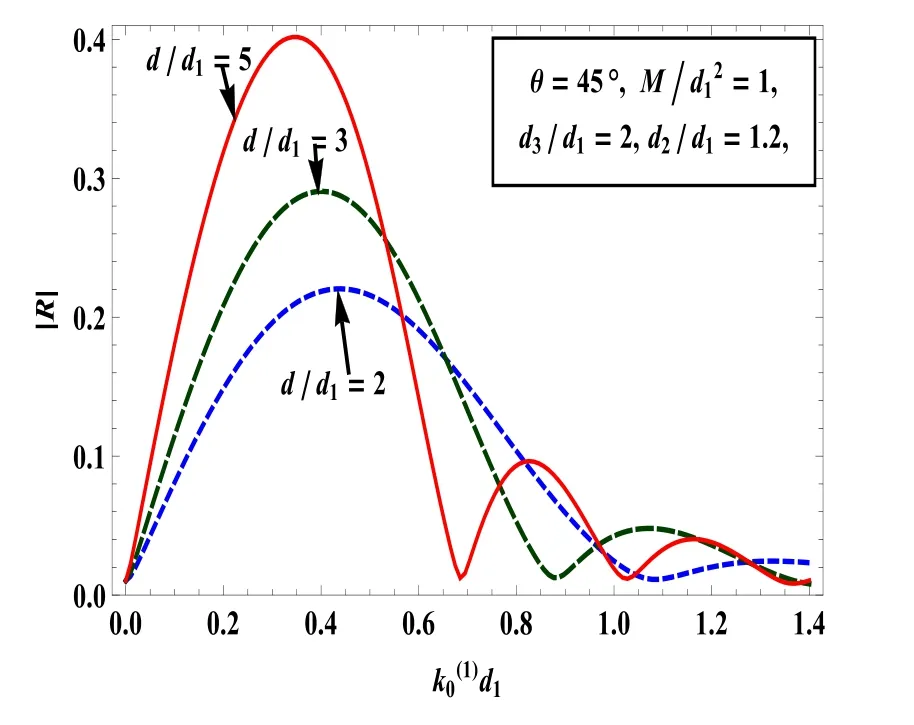
Fig.9.|R|for different values of width of the asymmetric trench in presence of surface tension.

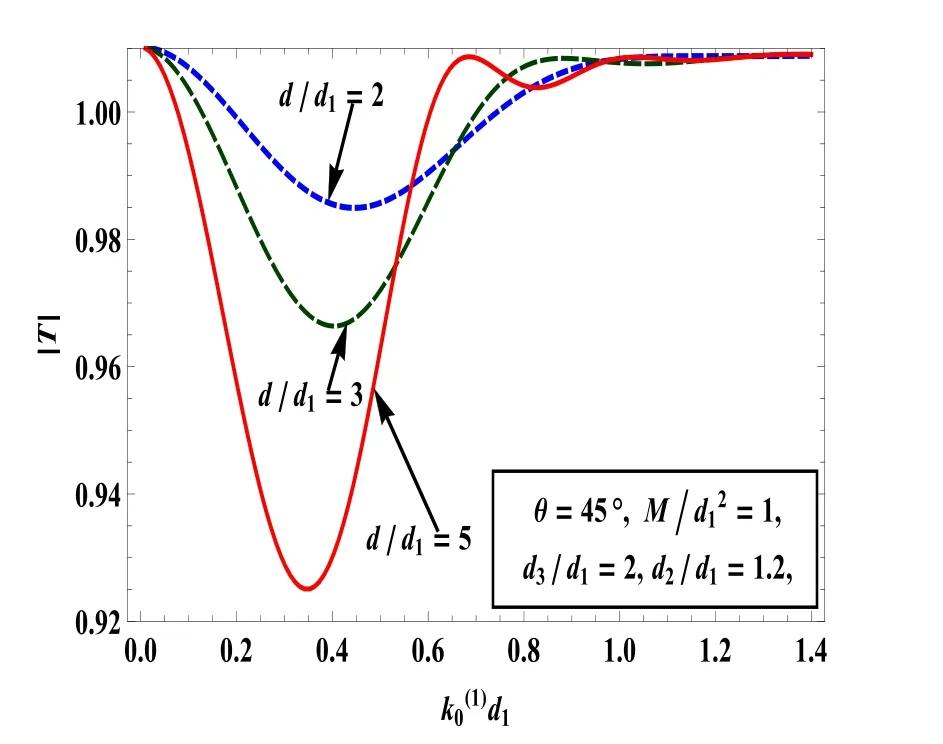
Fig.10.|T|for different values of width of the asymmetric trench in presence of surface tension.

The reflection and transmission coefficients are depicted againstfor varies values of width of the trench with fixed values ofin Figs 9 and 10,respectively.It is observed that the peak value of the reflection coefficient increases as the width of the trench increase.Fig.10 shows that|T|decreases as the width of the trench increases.It is also noted that the curve for reflection and transmission coefficients are oscillatory.It can be seen that the number of oscillation increases the width of the trench increases.

The effects of surface tension on reflection and transmission coefficients are shown in Figs.11 and 12,respectively.Graphs of these figures are depicted againstfor varies values of surface tension with fixed values ofFrom Fig.11,it can be seen that|R|is almost the same for a smaller value of＜ 0.2,however,|R|decreases with an increase of surface tension.It happens because of the cohesive force between fluid molecules at the free surface.Fig.12,reveals the fact that for small and large wave number,the incident waves are almost fully transmitted.

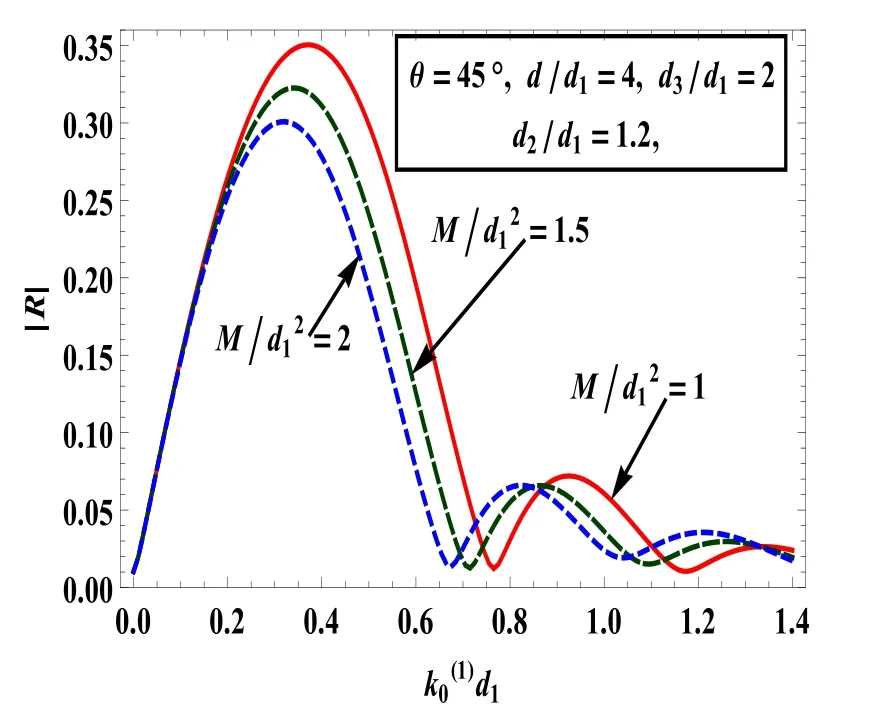
Fig.11.|R|against for different values of surface tension.

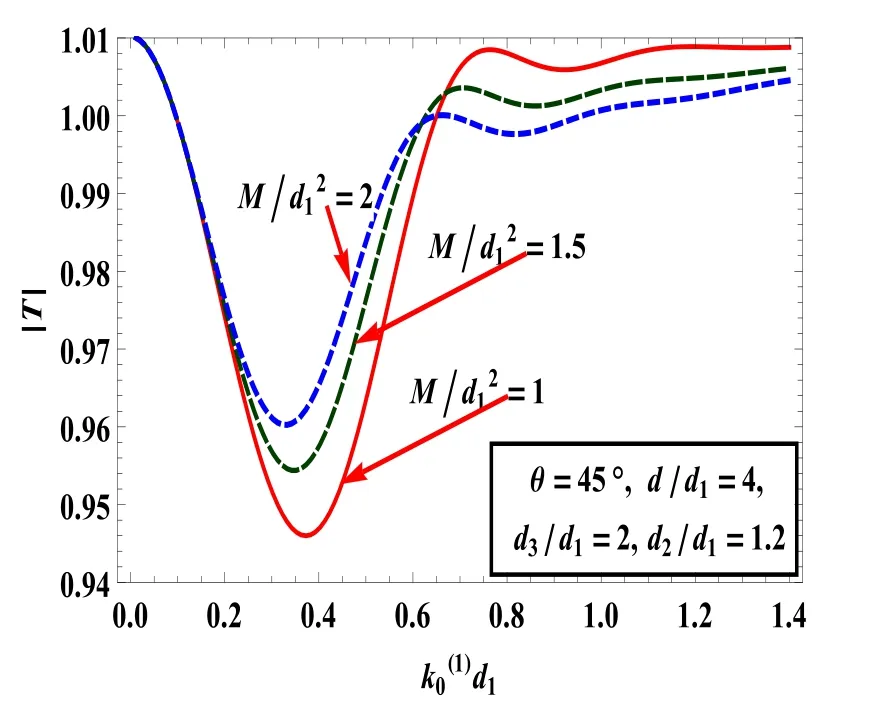
Fig.12.|T|against for different values of surface tension.

Fig.13.|R|for different values of depth of the asymmetric trench in presence of surface tension.

The graphs of|R|and|T|in Figs.13 and 14 are depicted againstwith fixed value ofθ=45o,and for different values of depth of the trench.It is seen that the peak value of reflection coefficient increases as the depth of the trench increases.

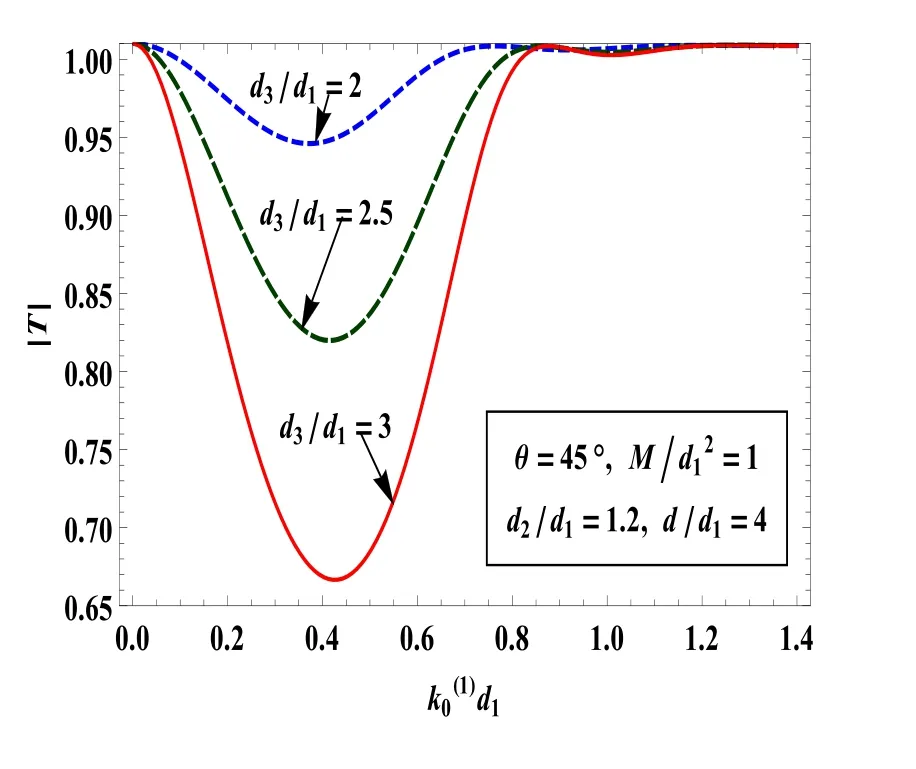
Fig.14.|T|for different values of depth of the asymmetric trench in presence of surface tension.

All these figures,it is clearly shown that|R|never vanishes at any frequency because the two sides of an asymmetric trench are not equal.The zero reflection phenomenon is not observed for the case of the asymmetric trench.It is also noted that the curve for reflection and transmission coefficients are oscillatory in nature.The oscillatory nature is attributed to multiple reflections of the incident wave train by two sides of the asymmetric trench.

7.Conclusion

The technique of(N+1)-term Galerkin approximations in terms of appropriate basis functions involving ultraspherical Gegenbauer polynomials has been utilized in this paper to obtain accurate numerical estimates for reflection and transmission coefficients in oblique water wave diffraction by an asymmetric trench in presence of surface tension at the free surface.An energy identity equation is derived using Green’s integral theorem in the fluid region of the problem.The derived result coincides analytically and graphically with the results that have already been presented in the literature.From the results,it is observed that surface tension has significant effects on wave reflection and transmission.In the presence of surface tension,the length and depth of the trench play an important role in the scattering behavior of the surface waves by an asymmetric trench.The multiple reflection’s phenomena are observed but zero reflection does not occur.From the results of wave transmission and reflection,it is seen that there exist zeros of reflection for some wavenumbers at which waves are fully transmitted corresponding to symmetric trench but for asymmetric trench full transmission does not occur.

Declaration of Competing Interest

The authors declare that there is no conflict of interests regarding the publication of this paper.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The authors would like to gratefully acknowledge the Editor and Reviewers for their valuable comments and suggestions to improve the quality of the manuscript.This work is partially supported by Higher Education,Science and Technology and Bio-Technology,Government of West Bengal Memo no:14(Sanc.)/ST/P/S&T/1 6G-38/2017.