雾化器转轴振动特性研究

尹自超 李明 陈波 李映辉

（西南交通大学力学与工程学院，成都 610031）

引言

喷雾干燥技术在相关产业已广泛运用［1-3］.国内常用的雾化形式有气流喷嘴式雾化、压力式喷嘴雾化和旋转式雾化，其中旋转式喷雾器在工业上运用最广泛［4］.转轴是旋转式喷雾器的重要部件，其转速可达（1～4）×104r/min，此转速范围已超过一阶临界转速，甚至达到二、三阶临界转速［1］.为解决转轴位于临界转速时的共振问题，唐等［5］基于传统的两点支撑模型提出了三点支撑模型.黄等［6］对三点支撑轴系进行了数值研究，给出了轴承在工作转速下振动节点的布置原则，有效避开了转轴的临界共振点.传递矩阵法在转子动力学发展史上占有重要地位，霍尔兹（Holzer）利用传递矩阵法解决了多圆盘转子扭振问题的初参数法［7］，而梅克斯泰德（Myklestad）和蒲尔（Prohl）将传递矩阵法用于求解转子的弯曲振动问题［8，9］。传递矩阵法具有占用空间小，算法简洁，矩阵维数不随系统自由度的增加而增大等优点，使其成为解决转子动力学问题的一个快速而有效的方法.

目前文献中未见讨论转速、雾化轮质量以及约束刚度等参数对转轴振动特性的综合影响，本文将综合考虑以上因素对雾化器转轴振动特性进行分析.

1 雾化器转轴模型

对图1（a）所示雾化器结构，为研究其转轴振动特性，可将雾化器转轴简化为图1（b）示由转轴、上下轴承约束、陶瓷约束和雾化轮组成的系统.将质量连续分布的转轴离散为有n个集中质量的自由度系统，相邻两节点用无质量的弹性轴段连接，上下轴承约束和陶瓷约束简化为刚度分别为k1、k2和k3的支撑弹簧，上下轴承间距为L，雾化轮简化为集中质量m（d），如图1（c）所示.

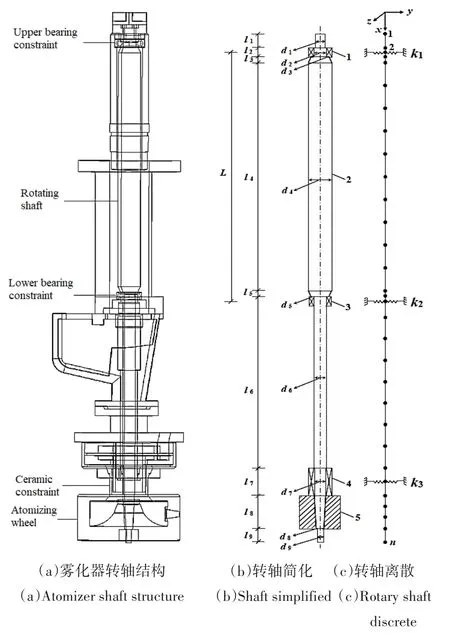
图1 雾化器转轴结构和简化图1—上轴承约束；2—转轴；3—下轴承约束；4—陶瓷约束；5—雾化轮Fig.1 Atomizer shaft structure and simplified diagram1—Upper bearing constraint；2—Rotating shaft；3—Lower bearing constraint；4—Ceramic constraint；5—Atomizing wheel

2 计算原理

2.1 等效质量与转动惯量

对图2（a）所示等截面轴段的质量及转动惯量为：

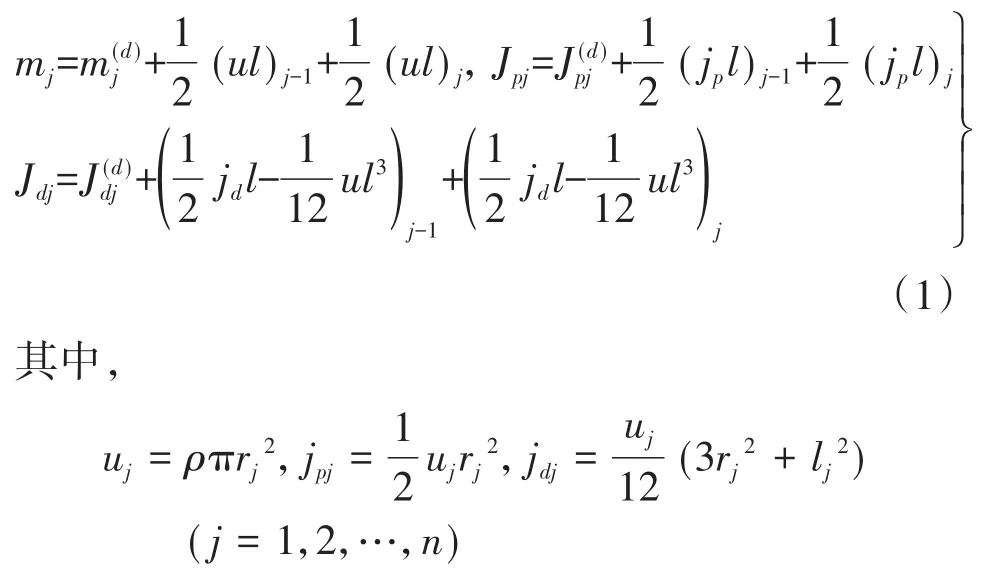
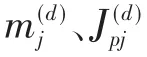
若第j轴段由n个截面不同的子轴段组成，如图2（b）所示，将第j轴段的质量和转动惯量附加在轴段的两端，轴段简化为只有刚度的等截面弹性轴，则：

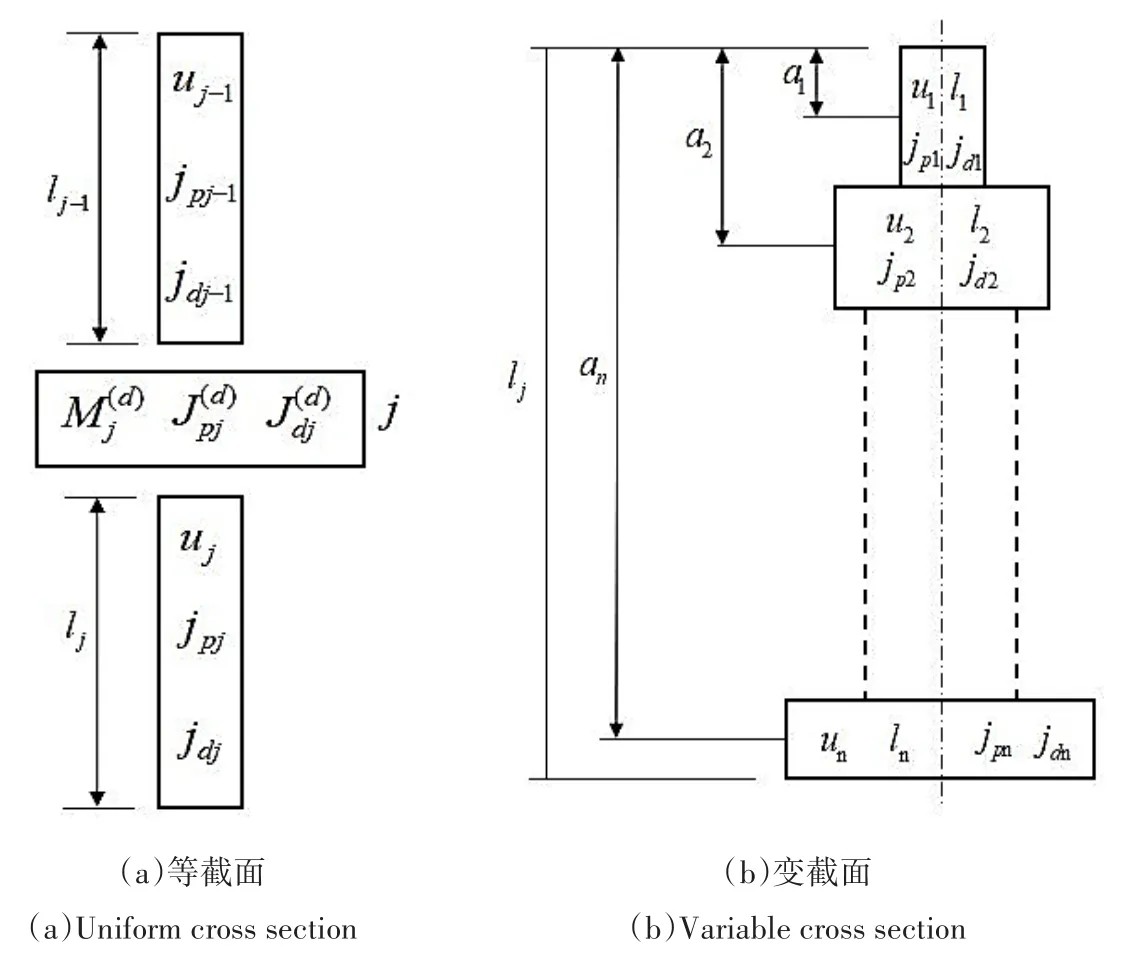
图2 等截面和变截面轴段的质量和转动惯量Fig.2 Mass and moment of inertia of equal and variable cross section

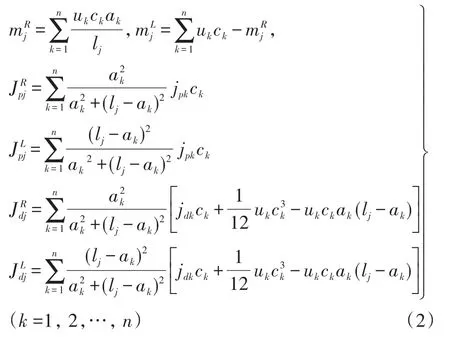
式中ck、ak和lj分别为子轴段的单位长度、子轴段的质心到该轴段最上端截面的距离和整个轴段的总长.对于第j个节点，集中质量和转动惯量分别为：

2.2 轴段间传递关系

对第i轴段及该轴段上下两节点受力如图3所示，上下两个节点编号分别为i和i+1，此轴段两端的截面挠度y、转角θ、弯矩M和剪力Q关系为：

图3 第i个轴段受力图Fig.3 Force diagram of the ith shaft segment

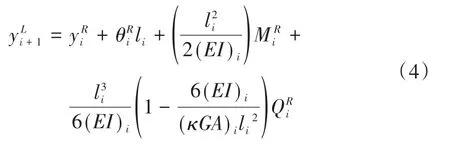
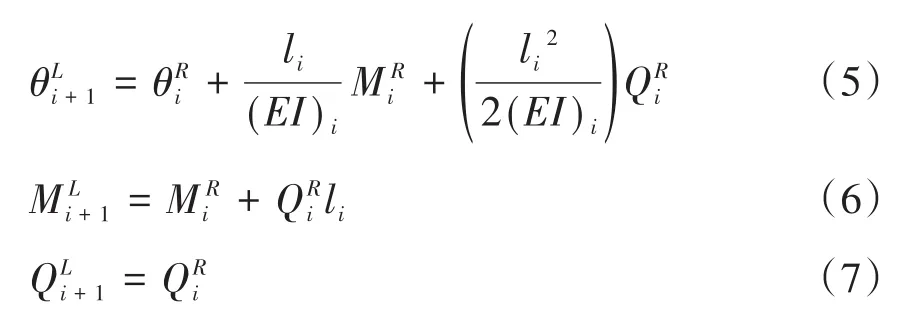
式中（EI）i为轴段截面抗弯刚度，（G）i为剪切弹性模量，（A）i为轴段横截面积，（κ）i为截面形状系数，对空心圆截面取2/3，实心圆截面取0.886.截面状态向量用｛δ｝表示为

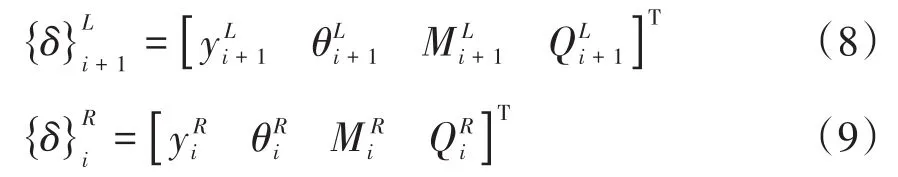
由式（4）～（7）可将式（8）和式（9）建立如下关系：

其中［TF］i是由式（4）～（7）得到的系数矩阵

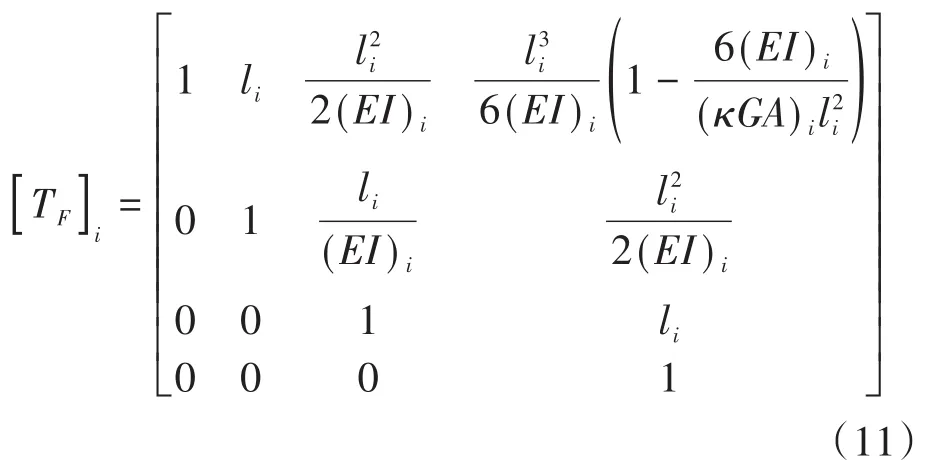
式（11）为第i轴段的传递矩阵，而对第i节点挠度y、转角θ、弯矩M和剪力Q关系为

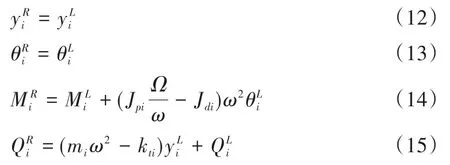
式中kti为节点处的弹簧刚度，JpiΩω为陀螺力矩.节点i的状态向量｛δ｝为

由式（12）～（15）可将式（16）和式（17）建立如下关系

其中［TS］i是由式（12）～（15）得到的系数矩阵

式（19）即为第i节点的传递矩阵，将式（18）代入式（10）有

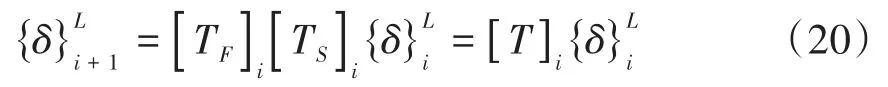
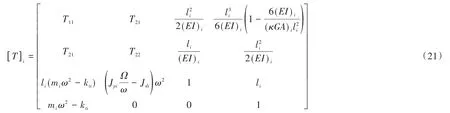
式（21）为第i轴段的最终传递矩阵，其中

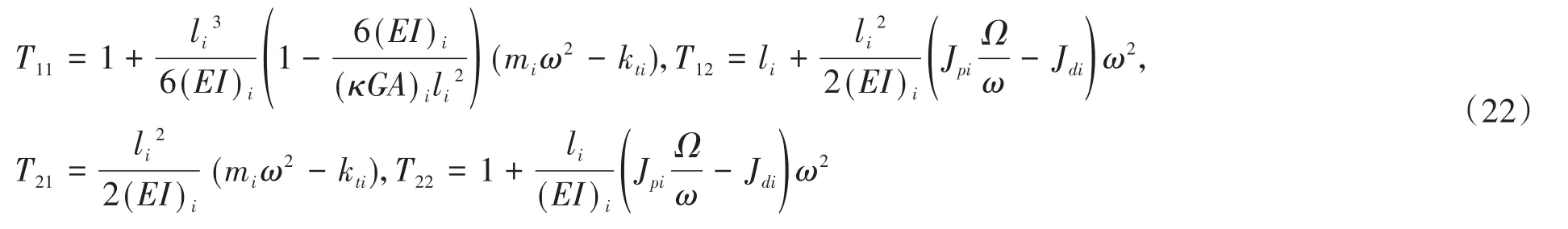
重复运用（20）式可得

式（24）为整个雾化器转轴的传递矩阵，它是一个4×4阶方阵，n表示轴段总数.当转轴两端自由时，两端截面状态向量为

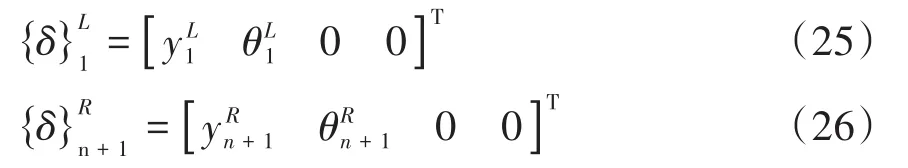
将式（25）、（26）代入（23）有

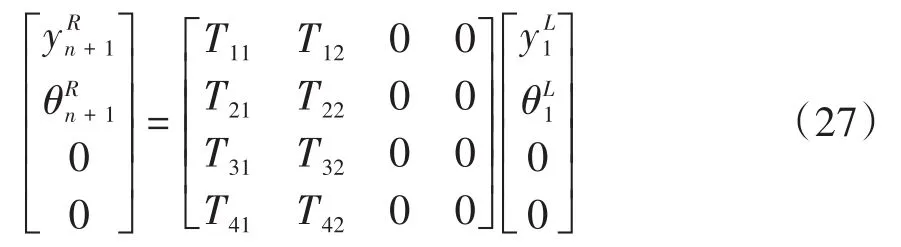
由式（27）有

式（28）、（29）为一个齐次代数方程组，该齐次代数方程组存在非零解，因此，其系数行列式为零，故得转轴系统的频率方程为

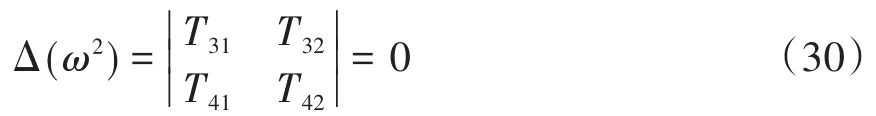
式（30）为两端自由雾化器转轴的频率方程.

3 数值仿真和讨论

3.1 验证

为验证方法的正确性，采用二节点梁单元建立有限元模型进行模拟（如图4），并与本文方法进行对比，有限元模型中单元数为10628，节点数为10629.雾化器转轴几何和材料参数如表1和表2所示.

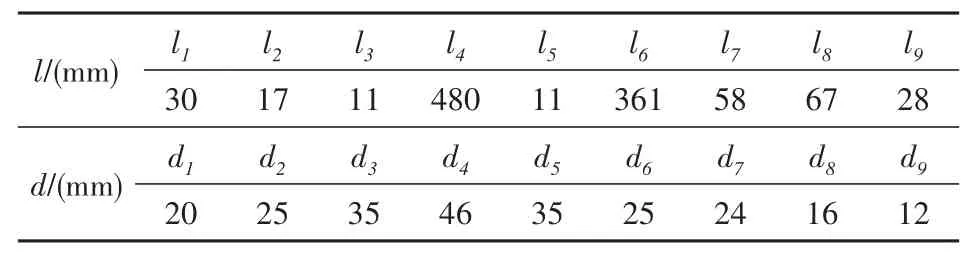
表1 雾化器转轴几何参数Table 1 Geometry parameters of the atomizer shaft

表2 雾化器转轴材料参数Table 2 Material parameters of the atomizer shaft

图4 雾化器转轴的有限元模型Fig.4 Finite element model of atomizer shaft

表3 本文解和有限元计算结果对比Table 3 Comparison of the present solutions and finite element method（FEM）calculation results

下面讨论各种参数对雾化器转轴振动特性影响，计算中转轴几何参数和材料参数仍如表1和表2所示.

3.2 转速的影响

图5给出了转速Ω对雾化器转轴前四阶涡动频率的影响，计算中上下轴承约束为刚性约束k1=k2=∞，陶瓷约束刚度k3=20000N/mm，雾化轮质量m（d）=0.0184t.由图 5 可见，由于存在陀螺力矩的影响，随着转速Ω的增大，转轴前四阶涡动频率出现正进动与反进动的现象，而当Ω=0r/s时，陀螺力矩消失，此时正进动频率等于反进动频率.当转速增加时，对于正进动，陀螺力矩使转轴的变形减小，提高了转轴的刚度，进而使其频率增大；而对反进动，陀螺力矩使转轴的变形增大，降低了转轴的刚度，进而使其频率减小，特别地，转速对高阶（如三、四阶）频率影响相对较小.

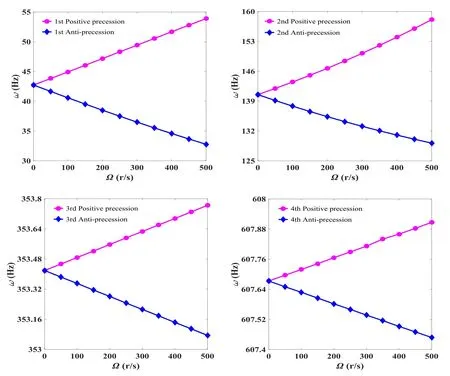
图5 转速对涡动频率的影响Fig.5 The effects of speed on the vortex frequency

3.3 雾化轮质量的影响

图6给出了雾化轮质量m（d）对雾化器转轴前四阶涡动频率的影响，计算中Ω=200r/s，上下轴承约束为刚性约束，k1=k2=∞，陶瓷约束刚度k3=20000N/mm.由图6可见，随雾化轮质量的增大，前四阶涡动频率都在减小，当雾化轮质量继续增大时，正进动与反进动频率曲线逐渐变缓，说明其对涡动频率的影响逐渐减小.从图中亦可见，雾化轮质量的变化对一、二阶涡动频率影响较为明显，当雾化轮的质量增加至0.045t时，其涡动频率变缓趋势并不明显；而雾化轮质量的变化对三、四阶涡动频率影响较小，当雾化轮的质量增加至0.045t时，其涡动频率的变化趋势较为平缓.

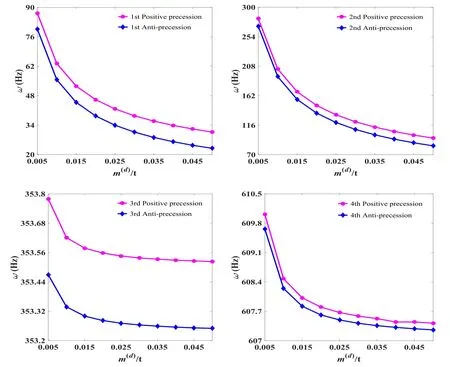
图6 雾化轮质量对涡动频率的影响Fig.6 The effects of atomization wheel mass on the vortex frequency

3.4 陶瓷约束刚度对临界转速的影响

图7给出了陶瓷约束刚度k3对雾化器转轴前四阶临界转速的影响，计算中Ω=200r/s，上下轴承约束为刚性约束k1=k2=∞，雾化轮质量m（d）=0.0184t.由图7可见，陶瓷约束刚度k3小于5000N/mm时对一阶临界转速有明显影响，二阶、三阶和四阶临界转速整体上随陶瓷约束刚度k3的增大呈缓慢增加趋势，其中二、四阶临界转速增加幅值较大，而第三阶涡动频率因不动点与下轴承约束重合，导致陶瓷约束刚度k3的变化对三阶临界转速影响很小.

图7 陶瓷约束刚度对临界转速的影响Fig.7 The effects of ceramic confinement stiffness on the critical speed

4 结论

本文基于Timoshenko梁理论，利用传递矩阵法计算了雾化器转轴前四阶涡动频率，研究了参数对其振动特性的影响，得到以下结论：

（1）转速大于0r/s时，由于存在陀螺力矩的影响，雾化器转轴的前四阶涡动频率出现正进动与反进动的现象，且转速对高阶（如三、四阶）涡动频率影响较小；

（2）雾化轮质量增大，雾化器转轴的前四阶涡动频率减小，且雾化轮质量对一、二阶涡动频率影响较大，而对三、四阶涡动频率影响较小；

（3）陶瓷约束刚度对雾化器转轴二、四阶临界转速有明显影响，对第三阶临界转速影响最小.