多体系统动力学的常用积分器算法*
2021-05-20任辉周平
任辉 周平
(哈尔滨工业大学航天学院,黑龙江 150001)
引言
多体系统动力学得到的动力学方程组是微分代数方程组(Differential-Algebraic Equations,简称DAEs),其一般形式特别复杂.为了简单起见,本文以最典型的index-3的完整约束DAEs:

为主要对象,介绍一下常见的通用型软件积分器的常用算法与实现细节.通常来说,通用型多体动力学软件的积分器主要强调以下几个方面的特性:
(1)精确性.通过控制积分过程的局部误差,可以大致保证计算结果的正确性和精度;
(2)高效性.在满足给定的误差条件下,自适应地选择尽可能大的积分步长,保证计算速度;
(3)鲁棒性.积分器应当可以稳定求解所有常见类型的多体系统动力学方程组.
通用型软件中的动力学方程组在形式上要比方程组(1)繁琐得多.除了完整约束方程组之外,很多实际系统中还包含非完整约束方程组、控制器方程组(一阶常微分方程组或代数方程组)、离散时间方程组等等.但从数值方法的角度来看,最复杂也最难求解的还是类似方程组(1)的index-3的微分代数方程组.因此,本文主要以方程组(1)为分析对象,而只在文中简要讨论一下其他情况,主要是带非完整约束的DAEs的求解方法.
本文只强调适合大规模多体系统动力学仿真软件的通用型积分器技术,而不详细讨论针对某些专门问题的特殊积分器技巧.在通用型软件中,积分器一般是作为独立模块开发的,主要用来宏观控制求解进程,而尽量少与其它模块在底层交互.软件中的方程组模型一般是提前设定好的.当软件的积分器模块开发调试完成后,一般很少再作大的修改.随着求解问题领域和规模的扩大,当软件架构需要扩展升级时,积分器模块往往也需要整体重新设计和开发,此时亟需整理和消化前人开发过程中发展出来的技术.因此积分器模块中求解技术的维护和传承非常重要.还应该指出的是,尽管积分器的理论对程序的开发有绝对的指导作用,但好的积分器中的绝大部分有效的技术细节往往都来自实践中的反复测试、改进和提供,而非理论公式推导本身.
本文尽量整理了作者在科研和程序开发中学习和体会到的积分器的一些技术细节.文中绝大部分积分器都经作者亲自开发并测试过,希望能对我国自主研发多体系统动力学软件有所帮助.
动力学方程组的特性分类
动力学过程是非线性时变的.积分器必须能够自适应地追踪系统的时变特性,并选择合适的时间步长来复现真实的物理过程.要做到既不能错过重要的物理现象,也没必要采用过密的时间节点而浪费大量计算资源.尽管待求解的方程组都是方程(1)的形式,但在仿真计算过程中,由于具体系统的动力学过程千差万别,积分器的表现也是非常不同的.从动力学特性上来说,多体系统仿真中常见的DAE系统大致可以分为以下几类:
(1)刚体为主导的系统.这类系统在大型多体系统动力学中最为常见.由于建模方法不同,所得方程组的数学特征也稍有不同.
•通过递归(recursive)公式建立的动力学方程组,其主要特点是:方程的非线性很强,表达式相当复杂;其Jacobian矩阵经常为满阵,但其规模相对较小.
•由绝对坐标描述,通过拉格朗日方程建立的方程组,其主要特点是:约束方程的个数很多,可能与动力学方程的个数为同一量级;刚体之间的相互作用绝大部分由作用力和约束方程来描述.
一般来说,多刚体系统方程的刚性问题往往并不严重,而且光滑性比较好,往往可以用高阶格式并结合比较大的时间步长进行数值积分.
(2)柔性体动力学为主导的系统.一般来说,在这种多体系统中,刚体的个数仍然远多于柔性体的个数.但每个刚体只有6个自由度,而每个柔性体的模态坐标个数可能比较多.更重要的是,模态坐标对应的固有频率可能很高,会在DAE系统中引入比较强的刚性,导致Jacobian矩阵的条件数比较大.实践中发现,积分器本身的耗散往往不能有效地衰减模态坐标对应的高频振动,因此推荐在模态坐标中引入少许线性阻尼或结构阻尼以提高仿真计算效率.
(3)大变形体为主导的系统.通常包含用几何精确方法或者绝对节点坐标方法建立的大变形有限元模型,需要引入几何非线性和/或材料非线性的影响.这类系统的动力学方程个数通常远远多于约束方程个数,且方程组主要由二阶动力学方程组成,具有特殊的稀疏格式.一般说来,从结构动力学中发展出来的方法,例如广义α方法或者HHT方法,在求解这类问题中被证明是很有效的.
(4)接触碰撞过程为主导的系统.在散体颗粒系统或者传动系统的动力学仿真中,经常会遇到这一类系统.首先,由于方程结构的变拓扑性,稀疏矩阵求解器的符号LU分解不再能复用,而根据具体条件进行矩阵LU分解是计算中所必需的.其次,常用的罚函数方法得到的接触碰撞动力学方程组的刚性和高频振荡问题都比较严重.最后,这类系统仿真过程对于接触体的几何形状和接触模型比较敏感,采用不同的算法求出的接触力可能差异比较大.
(5)有特殊要求的一些多体系统.例如在虚拟现实仿真中,要求做到实时仿真,需要用到实时积分;高速旋转系统中,需要对转动进行有效精确描述;长时间运行的无耗散系统,对能量守恒要求比较高,需要用到守恒格式的积分器;对最优控制设计得到的系统,可能需要求解的并非初值问题,而是边值问题等等.这些问题将不在本文中详细讨论.
实际中遇到的大型多体系统仿真问题,往往是上述几种类型的组合.因此实践中需要的通用型积分器,要求能同时求解所有这些类型的方程组.此外,具体的应用场合也非常重要,而不同场合考验的是积分器不同方面的特性.例如,很多设计过程需要反复进行大量的动力学仿真以优化产品的动力学性能;而在另一些场合中,实时仿真的要求可能更加重要.一个优秀的通用型积分器应该在求解常见应用问题的时候具有高效性,而同时在不常见的特殊应用中也应该具有鲁棒性.
常见通用型DAE积分器简介
通用型DAE积分器需要有能力做到:
(1)自适应地选择积分步长;对于变阶积分器,还需要自适应地选择阶数;
(2)有效地进行误差估计,既可用于保证计算精确性,又可用于变阶变步长;
(3)不连续性和不稳定性现象的检测与处理,自动进行算法调整和事件解决;
(4)有效处理由于数值原因导致的速度、加速度、拉格朗日乘子曲线的不光滑性;
(5)在奇异位形、不光滑点处积分器遇到无法解决的问题时可以自动重启.
所有的DAE积分器都源自相应的常微分方程(Ordinary Differential Equations,简称 ODEs)积分器.但DAEs与ODEs在数值特性上有很大的不同[1],而求解算法的理论和程序实现细节也不同.
常用的通用型DAE积分器大部分都是隐式格式,其主流算法通常认为主要有三大类:基于向后差分公式(Backward Difference Formula,简称BDF)的积分器族,基于广义 α(Generalized-α)方法的积分器族,与基于隐式龙格库塔(Implicit Runge-Kutta,简称IRK)方法的积分器族.这些方法可以直接求解DAE方程组(1)或其变形.此外,将DAEs转化为ODEs并采用ODE积分器来进行计算也是重要的DAE求解思路.
BDF族积分器包含了一系列变阶变步长积分器.其具体的公式有好几种变形格式[2-4];求解的DAE方程组的index可以为1、2或者3;截断误差的阶数可以从1阶到5阶.对于光滑性比较好的多体系统,例如没有接触碰撞的多刚体系统,可以用高阶格式结合大的时间步长进行积分,求解效率非常高.这类方法的缺点是其低阶格式对低频运动的阻尼比较大,因此如果系统的光滑性不太好,其动力学响应可能会有比较大的衰减.Gear[5]最早将刚性ODEs求解中常用的BDF方法引入到index-1的微分代数方程组的求解中,并将其应用于电路系统和化学过程的动力学仿真.Orlandea等[6]将其进一步推广到了多体系统动力学的应用场合.经过深入研究,Brenan等[7]从数学角度证明了BDF方法在一般index-1和index-2 DAE系统中的收敛性;同时指出[8],对于一般的index-3的DAE系统,该方法的收敛性不能从理论上得到保证.但大型商业软件的实践证明,在一定限制条件下[9],BDF方法完全可以用来求解index-3的多体动力学方程组(1),而且到目前为止该方法在所有方法中似乎是相当高效的.工业界中,BDF方法仍然是一些大型商业软件的缺省求解器,甚至在很多结构动力学的应用场合,其性能仍然非常卓越.直接用BDF积分器求解方程(1)遇到的最大问题是速度变量的误差估计比较困难[10,11].这是因为Jacobian矩阵的条件数很大,求解带来的舍入误差会严重污染速度变量的截断误差,往往会导致对速度变量无法进行有效的误差估计.这一问题有几种解决方案,投影滤波方法[11]即是其中之一.Gear等[12]证明,index-3的多体动力学系统可以等价地转化为数值特性更好的index-2的DAE系统,因此可以更稳定地利用BDF方法求解.实践表明,这样求解的结果精度更高,尤其是速度和加速度的连续性和光滑性更好.但同时,得到的index-2的DAE系统的方程规模会更大,因此计算量会稍微大一些.BDF积分器在实践中还有很严重的问题;三阶以上的BDF格式不是绝对稳定的,因此在求解宽频动力学问题时很容易有频率进入不稳定性区域,导致阶数和步长的估计不再可靠.在某些应用场合甚至需要手动设置最大阶数为2才能顺利计算下去,非常不方便.如何自适应地选择积分器的阶数来避免不稳定性问题,这一方面的研究也已取得了一些进展[13,14].作者认为,BDF 族积分器的性能还存在着一定的提升空间.
近年来,广义 α 族方法[15],包括作为同类格式的HHT方法[16],受到了更多人的研究和使用.这类方法是传统Newmark方法的高精度扩展,具有统一的二阶截断误差精度.与BDF方法不同,这种方法计算中用到了位置、速度与加速度之间的关系,可以直接离散二阶动力学方程组;计算中修正的量本质上是加速度和拉格朗日乘子.这类方法具有低频不衰减而高频衰减的优良特性[17,18],鲁棒性很好,特别适合求解结构动力学问题或者柔性多体系统动力学问题等.此外,这种方法程序设计比较简单,且可以推广到 index-2格式[19].尽管经过推广,这种方法也被应用到了一阶动力学方程组,但其数值精度有所损失.最后,该族积分器的精度保持为一阶或二阶,对于光滑的动力学系统,计算效率偏低.
隐式龙格库塔算法[20,21]也可以用来求解大型多体系统.与广义α方法类似,这种方法也是单步法,其自动选步长的算法比较简单;同时,这种方法可以实现变阶,对于光滑的动力学系统,理论上也可以采用高阶格式结合大的时间步长来计算[22].隐式龙格库塔算法既可以直接求解index-3的DAE系统[23]例如方程组(1),又可以求解index-2的DAE系统[24],很适合多体系统动力学仿真的应用[25].这种方法的缺点是,高阶格式的方程规模比较大,对于大型系统计算效率不高.因此实践中的隐式龙格库塔算法大多采用对角格式(Diagonally Implicit Runge-Kutta,简称 DIRK)[26,27].数值实践发现,大部分高阶隐式龙格库塔格式在实际计算中事实上达不到理论上的阶数[28],而具有阶数饱和现象[29].最近这方面的研究有一些新的进展[30],其有效性还有待进一步的测试.到目前为止,大型通用型软件很少选择隐式龙格库塔方法作为主要的积分器算法,因此本文中也不再详细讨论其计算细节.
以上积分器求解DAEs时都会遇到如下困难:
(1)Jacobian矩阵的相关问题.例如在约束系统的奇异位形下,Jacobian矩阵可能是奇异的或近似奇异的;在刚性问题中,可能由于Jacobian矩阵条件数太大[31],带来计算精度的降低、误差估计的失败或其它数值问题;
(2)对方程组(1)的直接计算仿真过程中,隐含速度约束往往不能得到有效满足,而加速度和拉格朗日乘子的曲线往往会有强烈的不连续性(spikes现象).此外,约束方程本身的不光滑性也可能会带来数值计算中的严重困难;
(3)微分代数方程解的连续性往往弱于外激励的连续性[1],高频激励常常会导致计算结果出现一些数值不连续现象;而输入变量或者作用力在时间上的不光滑性会对积分器的鲁棒性带来很大的挑战;在接触碰撞等问题中,不连续性与高频激励同时出现,甚至会导致计算无法顺利开展下去;
(4)大多数积分器的误差估计和自适应步长选择策略都是基于动力学响应解的光滑性假设.在各种非光滑情形,步长估计可能无效,往往引起大量的计算失败,大大增加整体计算量.
除了上面的直接方法以外,将DAEs转化为ODEs并用ODE积分器来进行仿真的方法也由来已久.通常认为这类方法计算效率不高,鲁棒性也较差,因此很少应用于商业软件的实践.如果约束方程组足够光滑,Baumgarte降阶方法[32,33]常常计算效果也不错.其它的一些降阶方法要么结合积分步长选择罚因子[34],要么将结果在约束流形上投影[35]或用罚函数拉回[36],要么采用修正的动力学方程组[37],更详细的内容可以在综述文章[38]中找到.通常这些降阶方法会引入一些高频的自由度,需要用刚性积分器或者特殊的显式积分器[39,40]来求解.
坐标分解方法也是一种相当有效的方法,而且计算精度较高.利用约束方程将一部分广义坐标用和自由度个数相等的其它广义坐标表示出来,从而将动力学方程组(1)转化为 ODEs[41],进而进行求解.一般的多体动力学系统很难找到在仿真过程中一直适用的广义坐标,必须在某些时刻进行坐标转换.其广义坐标的选择可以采用流形方法[42]或者投影方法[43].Shabana教授团队提出的两步隐式稀疏矩 阵 积 分 法[44-46](two-loop implicit sparse matrix numerical integration,简称TLISMNI方法),在每一步积分中都要进行坐标分解,并保证其同时满足几何约束、速度约束和加速度约束.这类积分器计算精度很高,但每步计算量太大.如果能证实其积分步长可以取得相当大,足以摊平每步的计算成本,该方法也将适合用于通用型积分器.作者尚未对该类积分器的效果进行测试,因此这部分内容也将不在本文中多做讨论.
1 微分代数方程组的初始条件
与ODEs不同,DAEs的初始条件不能任意给出 .理论分析表明[8,10,21],DAEs的初始条件下约束方程需要非常高精度地满足,计算才能有效地开展下去.方程组(1)中的约束方程组为:

隐含速度约束

和加速度条件C̈(q,t)=0,即


实际问题提供的初始条件q0和q̇0不一定满足这些约束方程,其原因可能有以下几点:
(1)q0和 q̇0无法准确给出,或者由于人为原因导致错误的初值设定;
(2)实践中,初值往往是测量出来的.而一般测量误差远大于数值计算中要求的误差量级,导致初始约束方程不能满足计算的精度要求;
(3)设定的初始数据,其中有些量可能相对比较精确,而其它的可能并不精确.因而需要调整不精确的初始变量以满足约束方程;
(4)求解过程中可能只确保了几何约束(2)能精确满足,而速度约束和加速度约束不一定满足,导致积分器重启后的初始条件不合适.
初始条件分析的目的是优化初始数据,使各种约束条件都能精确满足,并算出初始加速度和约束力.在此之前,首先要确认约束方程组是适定的.
冗余约束分析
约束方程可能是冗余的,甚至是互相矛盾的.在建模过程中,有时也可能故意用冗余约束的方法来保证系统安装的完整性.冗余约束分析的目的是找出数值特性最好的一组约束方程组,而删除所有其它的冗余约束.冗余约束分析的基本方法是对Cq(q0,0)进行全选主元的LU分解,并选择一组最大程度线性无关的约束方程组,而其余的约束方程即被认为是冗余约束而舍弃.
初始奇异位形检测
多体系统动力学仿真偶尔会陷入奇异位形中.在一般的计算过程中,由于舍入误差的存在,多体系统滑入奇异位形的可能性比较小,一般不需要专门的处理.更常见的情形是,多体系统的初始位形本身就是奇异位形,导致在冗余约束分析中,有些非冗余约束可能会被误判为冗余约束而舍去.此时,仿真计算的模型并不是需要的物理模型,因此有必要进行初始奇异位形检测,从而将这些非冗余约束捡回系统.
初始奇异位形检测的算法是对初始位形进行摄动,然后重新进行冗余约束分析,验证得到的独立约束个数是否与原来相同.如果不同,说明初始位形有奇异性.发生了这种情况,需要给出警告,要求用户输入更多信息来选择初始位置.如果用户不能提供其它信息,就随机选择若干个与初始位形非常接近的摄动位形分别出发进行仿真计算,并验证它们的最终计算结果是否相近.
初始位形分析
给出初始广义坐标q0,希望求得适合约束方程的初始位形.这可以简单地通过求解优化问题:

而得出.其中Wq为对角权重矩阵,其权重可根据q0的先验知识而调整.一般对已知精确的分量,其对角权重取为106,而对于不确定的分量,其权重取为1.从方程(6)得到的优化方程组为

这可以用牛顿迭代法求解,初始迭代向量取为q0.迭代收敛后,用计算出来的q取代初始变量q0.初始位形分析一般只涉及完整约束和/或状态变量本身的约束表达式,而不需要用到非完整约束等其它形式的约束方程.
初始速度分析
给出初始广义坐标q̇0,为了求得适合速度约束方程的初始速度,可以简单地求解优化问题

其中Wv为对角速度权重矩阵,其权重系数也可根据先验知识进行调整.得到的优化方程组为
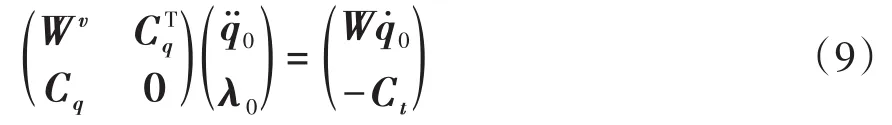
它完全是线性方程组,可以直接求解出满足速度约束方程组的初始速度.然后,用计算出来的q̇取代初始变量q̇0.应该强调的是,在一般情况下,方程(8)中也应该包括动力学系统所有非完整约束方程,因此通常也需要通过迭代才能求解.
初始加速度和约束力计算
很多积分器需要提供初始加速度和拉格朗日乘子的值,这可以由方程(1)和(4)计算出来:

通过初始值分析,既精简了约束方程,又得到了更合适的初始坐标 q0、速度 q̇0、加速度 q̈0和拉氏乘子λ0,是开展动力学仿真前的基础准备.
2 运动学问题求解方法
运动学问题是动力学系统的自由度为0的特殊情形.此时,约束方程组(2)足以决定整个系统的运动学.另外,此时Jacobian矩阵Cq(q,0)为方阵,且除了个别奇异位形以外是可逆的.运动学问题实际上就是用Newton迭代求解方程(2)
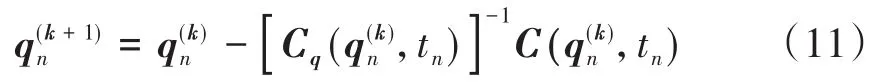
求解的过程要注意以下几点:

(2)理论上,迭代时间步长h可以任意选取,但考虑到初始估计(12)必须足够精确以保证Newton迭代(11)的收敛性,h也不能太大.
(3)由于Jacobian矩阵的生成和LU分解计算都比较昂贵,实用中常用拟Newton方法迭代.
计算得到了tn时刻的qn之后,可以进而求出tn时刻的速度,只需代入方程(3),即
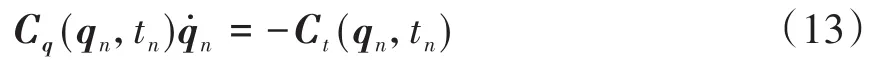
求解得出q̇n.更进一步,要求解tn时刻的加速度,需要用到方程(4),即

最后,很多应用中还需要算出约束力,只需求解

即可求出任意时刻的拉格朗日乘子λn,进而得到约束力.方程(13)、(14)和(15)中可使用同一Cq矩阵的LU分解.当然,运动学仿真在实用中只占很少份额,绝大部分问题还是需要动力学仿真方法,这将是下文的主要内容.
3 广义α族积分器
广义α方法最早是在结构动力学仿真中提出来的[17],它与稍早提出的HHT方法[18]实际上是等价的,而它们都是传统的Newmark方法的推广.这些方法都是单步法,其一般提法为:
问题 1:已知 tn时刻的状态变量 qn、q̇n、q̈n和 λn,及步长的估计h之后,求出tn+1=tn+h时刻对应的变量 qn+1、q̇n+1、q̈n+1以及 λn+1,并作出误差估计以判断其是否满足误差条件要求.如果满足,则估计下一步的时间步长;如果不满足,则估计更合适的时间步长,并重新开始计算.
传统Newmark方法可用来求解常微分方程

假设已知 tn时刻的 qn、q̇n和 q̈n,则在估计出步长 h 之后,只需将q̈n+1当作未知量,取近似

其中参数β和γ用来调节计算精度和稳定性,且

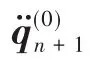

代入方程(16),得到关于x的非线性方程组

用Newton-Raphson方法迭代求解出修正量x,进而代入(19)中得到 qn+1、q̇n+1和q̈n+1.
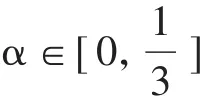

而tn+1时刻的状态变量假设为

其中公式(17)中的加速度替代为稍早时刻的值

而动力学方程组在较早的时间节点tn+1-α上离散

其中未知量为 an+1=q̈n+1-α,而

HHT积分器直接求解的并不是方程组(1),而是其变形格式(24),而且求解时间节点也不完全在tn+1时刻,利用an+1近似地插值得到tn+1时刻的加速度,就可以直接求解tn+1时刻的动力学方程组(1),得到的即为广义α积分器.这两种积分器的公式稍有不同,广义α积分器的参数稳定区域大于HHT积分器.除此之外,二者的各项性能都极其接近,误差估计与变步长策略也完全相同.本文将以广义 α积分器作为主要讨论对象.
在广义α积分器中,每步需求解的未知变量仍然是公式(23)中的an+1,但此时假设
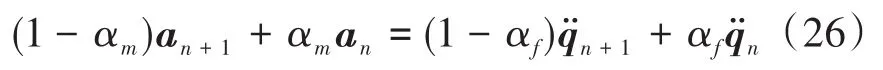
其中αm和αf两个参数一般并不相互独立,可以用一个自由参数ρ表示出来,取值 ρ∈[0,1].令

从方程(22)和(26)得出tn+1时刻的状态变量

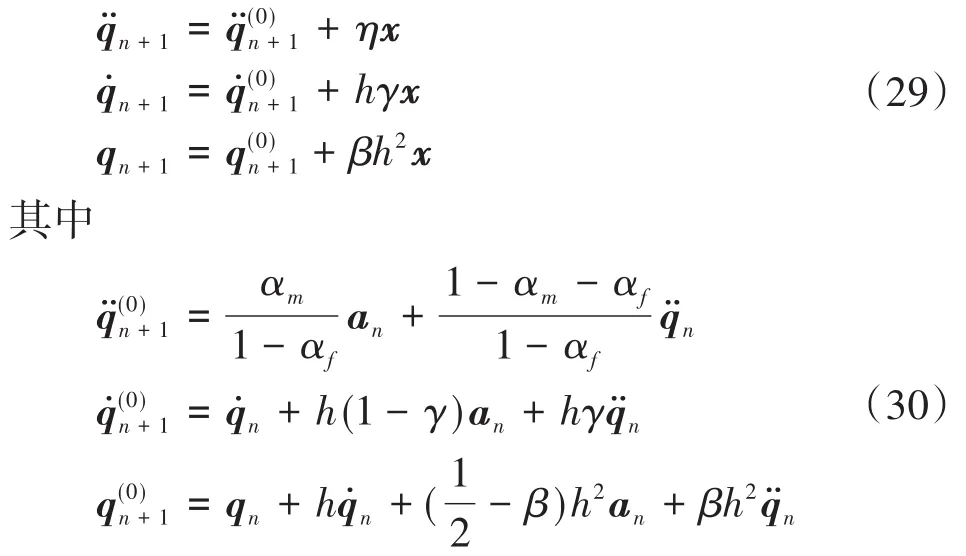
此外,假设乘子λ具有一定的连续性,即取
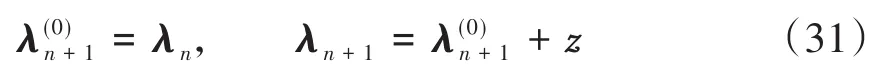
将表达式(29)和(31)代入方程(1),得到关于更新量x和z的非线性方程组

用Newton-Raphson方法求解,其Jacobian矩阵为
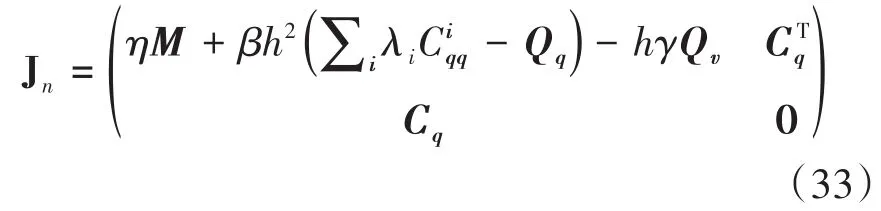
更新量x可以用来进行误差估计和步长选择.借鉴Negrut等[16]的推导,可以得出该方法的截断误差主项为ch2x;其中c为一个量级为1的常数.此外,由于广义α方法是二阶精度的,其广义坐标的截断误差正比于h3;而步长的选择应该满足每个分量的相对误差都小于但接近于设定的误差限,即

本文中的范数‖∙‖定义如下

如果Ξ>1,则说明误差条件没有满足,需要减小步长;而如果Ξ太小,则说明计算步长太小,会降低计算效率,最好放大步长.一个合适的步长选择策略是

其中系数0.9是安全系数.由于这里的计算是用本步得出的后验误差来估计下一步的积分步长,其正确性依赖于系统参数的缓变特性,因此安全系数是必要的.如果预测失败,即Ξ>1,则可以利用新得出的Ξ和方程(36)设置本步的计算步长重新进行计算.由于该估计误差为后验误差,得到的hnew一般能很好地满足误差条件.如果仍不满足误差要求,直接将时间步长减半重新计算;如果再不满足,说明在tn和tn+h之间出现了某种间断现象,需要进行间断检测,发现间断位置tn+h*,运行到该时刻然后重启积分器.广义α方法保持二阶精度,而且稳定性很好.以上的自适应步长选择策略失败率低,鲁棒性好,对很多间断情形也不需要积分器重启.由于间断性检测程序较复杂,在附录的算法3中将暂时忽略.
上述方法计算得出的加速度曲线和拉格朗日乘子曲线上经常会出现很多尖刺(Spikes),这种现象是非物理的随机误差,与所求解的方程组是index-3的DAEs有关.方程组(1)等价于
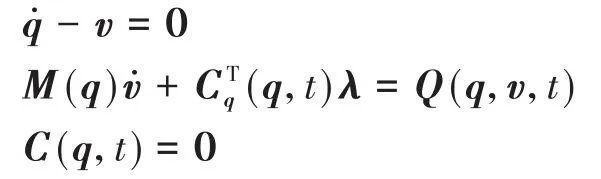
该方程需要在整个约束流形上满足,但数值离散格式不是在流形上开展的,而是在扩展的相空间(q,v)上进行的,这将导致如下问题:
1.即使方程q̇-v=0在约束流形的切丛上是点点满足的,该方程的离散格式往往已经稍稍脱离了约束流形,而进入了相空间;
2.尽管约束方程的引入强制保证了计算出的q̇近似位于约束流形上,但隐含的速度约束方程(3)却没有保证会被满足.

将q̇和v作为独立变量;根据流形上的常微分方程理论,可以将方程q̇-v=0换为约束流形上的等价格式;并将隐含的速度约束显式地引入方程组,得到新的动力学方程组

其未知量为q、v、λ 和 μ.该方程组是index-2的微分代数方程组,其与方程组(1)的等价性早已经被Gear等人[12]所证明.下面用广义α方法来离散方程组(37).此时,方程(26)和(28)中的速度项仍然被离散为

此时速度项vn+1与q̇n+1不再相同,但二者差别不应该很大,不妨假设
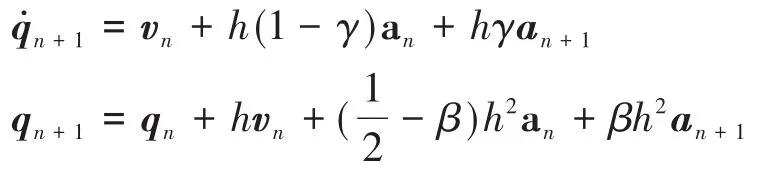
计算中,取an+1与an+1其预测值相同,且假设

进而类似方程(29)可以得出,

代入方程(37)得到

其未知量为x、y、λ和μ,迭代Jacobian矩阵为
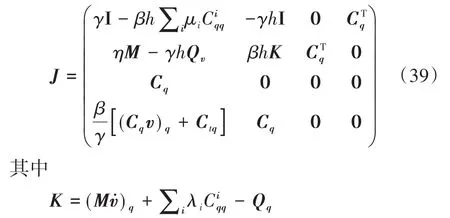
由方程(38)可以看出,x是与μ同量级的量.用截断误差分析可以证明[47],该积分格式是一阶的.该方法关于q的截断误差近似为hx,而关于v的截断误差近似为hy.同样记
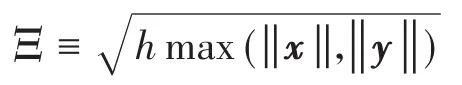
则Ξ≤1为误差判定条件;而新步长估计方法仍然基于公式(36).Jay和Negrut的分析表明[47],如果采用等时间步长积分,求解index-2方程组(37)的格式(38)是二阶精度的;但如果采用变时间步长积分,则离散格式(38)只有一阶精度.另外,他们还提出一种修正方法,可以将对应的HHT格式变为二阶精度的,而且该方法似乎也很容易推广到广义α方法.但作者还没有亲自测试证实,尚不知该方法的实践效果如何.
4 BDF族积分器
BDF族积分器有好几种公式实现[8].它一般用来求解常微分方程组和index-1、index-2的微分代数方程组[48],且结合一些特别的技巧后也能用来计算index-3的微分代数方程组(1).与广义 α方法不同,BDF方法是多步法,而且是一类变阶数、变步长的方法.多步法的一般提法为:
问题2:已知之前 k+1个相继时刻tn−i(i=0,1,…,k)对应的广义坐标 qn-i、速度 q̇n-i、加速度q̈n-i以及拉格朗日乘子 λn-i,在给出时间步长 h之后,求出 tn+1=tn+h 时刻对应的变量 qn+1、q̇n+1、q̈n+1以及λn+1,并给出计算误差的估计,判断计算结果是否满足误差条件.如果满足,则估计下一步的阶数和时间步长;如果不满足,则更新本步阶数和时间步长,并重新进行计算.
下面以常微分方程为例,介绍两套常用的BDF公式.常微分方程组的形式为:

准步长公式
假设给定一系列等步长为h的时间节点tn-k,tn-k+1,…,tn,tn+1,以及其对应的数据xn-k,xn-k+1,…,xn,xn+1.根据在以 h为步长的均匀时间网格上,后差分算子∇如下递归定义:
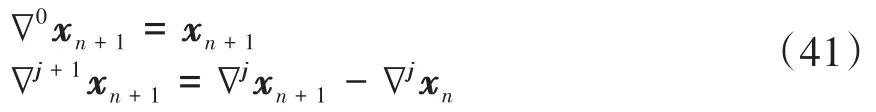
其中j=0,1,2,….用中值定理可以证明,存在某个ξ满足tn+1-kh≤ξ≤tn+1,使得

给定k≥1,记

递归地使用(41),可得∇kxn+1=∇kxn+δ,∇k-1xn+1=∇k-1xn+∇kxn+δ,…,其通项为
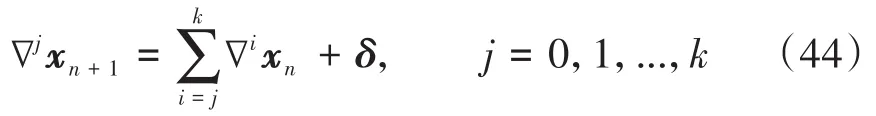
特别当j=0时有
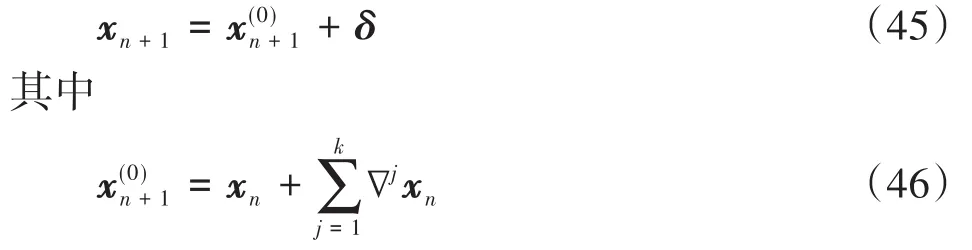
另外,可以直接验证[49]多项式

为唯一满足 ph(tn-j)=xn-j的k阶多项式,其中j=0,1,2,…,k;对此方程求微分可得
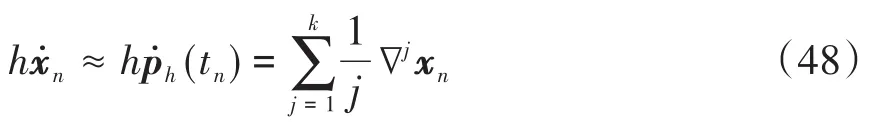
将近似表达式(48)中的n替换为n+1,得到



其中的常数为

为了与后文符号的统一,记

以及

则方程(46)和(50)可以改为
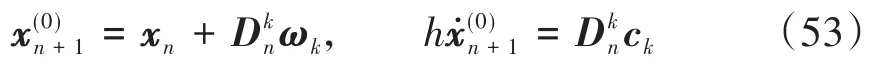

其中矩阵Rk和Uk为k× k的矩阵,其(i,j)分量分别为


参考公式(47),分别将t=tn-iζh(其中i=0,1,…,k)代入方程(56)得到k个线性方程:
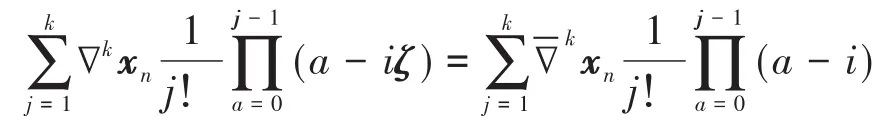
计算流程
(1)利用公式(53)得出 xn+1和 hẋn+1的初始估计,然后将(45)和(49)代入微分方程组得到离散格式,用Newton迭代求出更新量δ;
a)∇k+1xn+1=δ已经求得;
b)∇k+2xn+1=δ-∇k+1xn;
c)依次计算 ∇jxn+1=∇jxn+∇j+1xn+1,其中j=k,k-1,…,1;
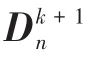
变步长公式
在这套公式下,均匀网格是不需要的,但理论推导要用到Newton插值公式:[xn]=xn

其中j=1,2,3,….可以用数学归纳法和中值定理证明,存在某个ξ,满足tn-k≤ξ≤tn

为了符号方便,对j=1,2,…,k+1,记

并且记(注意它与公式(41)中的定义没有关系)
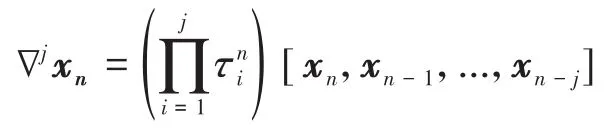
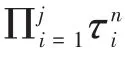

利用这个公式递归可得

以及


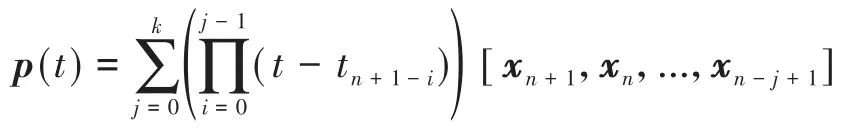
是唯一满足p(tn+1-m)=xn+1-m的k阶多项式,其中.直接微分上式可得

将公式(60)代入方程(62)中,简化得到
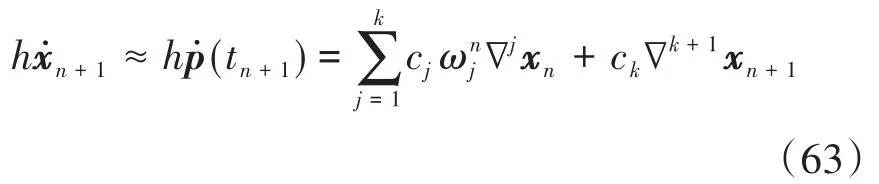

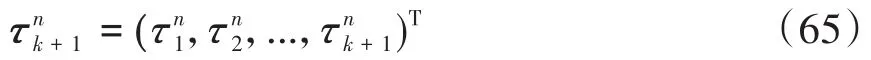

其中j=1,2,…,k+1.进一步,记
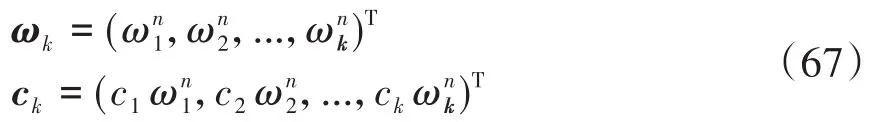
于是公式(61)和(63)可以写成

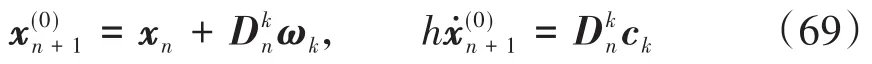

计算流程
变步长积分器的步进计算为:
(2)利用公式(69)得出xn+1和hẋn+1的初始估计,然后将(68)代入微分方程组得到其离散格式,再用Newton迭代求出更新量δ;
(5)令n←n+1,进入下一步循环的起始步1.
方程组求解细节
将表达式(45)和式(49)或者式(68)代入方程(40)得到关于δ的非线性方程组




求解方程组(1)用到q和v≜q̇的差分矩阵

从而这两个差分矩阵可以算出变量的估计表达式

因此,广义坐标的BDF预测-校正公式为

而对应速度变量的BDF预测-校正公式为


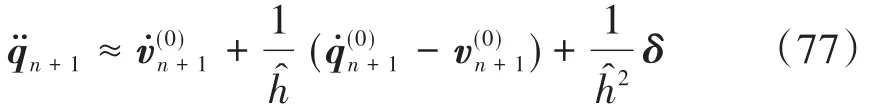
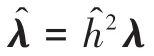

可以用Newton迭代法求解,其Jacobian矩阵为

求解得到的δ可以直接用来估计q的误差,但由方程(76)得出的ε用来估计q̇的误差却可能会被严重放大[10],需特殊处理后才能应用.这里介绍一种更新误差估计中的ε的方法,即投影滤波法.深入分析[11]发现,方程(76)计算出来的速度变量误差并不是沿所有方向都会被放大;而误差真正被放大的方向与约束流形的切空间正交.如果将ε投影到约束流形切空间内,即
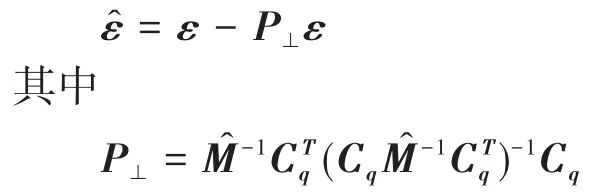


为了改进速度变量的误差估计,并减小加速度和拉氏乘子的计算误差,可以将方程组(1)转化为与其等价的index-2的方程组[12]

然后用BDF积分器进行求解.该方程组的规模比直接求解方程组(1)大了一倍,所需的计算量也大了很多.具体计算步骤为:将变量的离散格式

以及时间导数项的离散格式
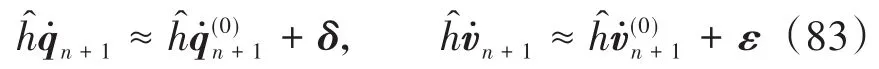
代入方程组(81),得到离散代数方程组为


在求解以上Index-2微分代数方程组并得到ε和δ后,就可以同时判断 ε和 δ相对于q和v的误差是否满足计算要求.计算得出的qn+1和vn+1都是准确的,但拉格朗日乘子λn+1和加速度
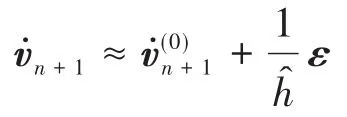
可能还是误差较大.为了进一步提高计算精度,可以将 q、v和 a=v̇都变成 index-1 的变量,即方程(81)修改为

该方程组仍然是index-2的DAEs,但其对应的index-2的变量为较次要的λ、μ和τ,而所有重要的变量q、v和a都是index-1的变量,在计算中都可以精确地计算出来并进行误差控制.
变步长变阶
BDF方法是变阶变步长的,可以根据本步计算的后验误差进行下一步的阶数和步长的估计.早期的 BDF 族 ODE 积分器,例如 DIFSUB[50]或者LSODI[51]中,通常建议k阶格式等步长运行k+2步之后再变阶变步长.但在通用型DAE积分器中,为了及时捕捉系统的时变特性,建议每一步都要变阶和变步长.为了方便讨论,记

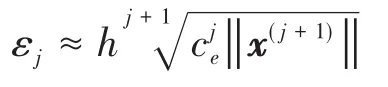
作为下一步计算步长仍为h时对应的j阶格式的误差预测,利用某种规则选择下一步最合适的阶数和时间步长.计算所需的相关数据都含在矩阵

中,其中备选的阶数为 j=1,2,···,k+1.因此,每步计算中可以随时降多阶,但至多只能升1阶.这样一来,积分器既可以在处理意外(不光滑)事件过程中做到自适应降阶;又可以在求解光滑的动力学过程中根据需要将阶数逐渐增加,提高仿真效率;达到了高效性与鲁棒性之间的有效平衡.
阶数和步长的选择有很多方法,最简单的思路是选择阶数使下一步的预测步长最大,即选择
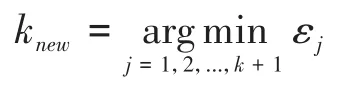
和对应步长hnew=0.8∙h/εknew,其中0.8为安全系数.这种方法实现容易,其各种变形或修正格式在通用型软件的积分器中仍被广泛采用.
一般来说,BDF低阶格式计算效率低,而高阶格式(特别是k≥3的格式)的稳定性较差.此外,如果保持阶数和步长,则上一步的Jacobian矩阵往往可以复用,会节省不少计算量.因此在新的阶数和步长的选择中,一般采用如下原则:尽量不变阶也不变步长;升阶时候尽量保守.例如:
(1)在Gear的程序DIFSUB[49]中,每步要求升/降阶次都不超过1.如果本步的阶数为k,在进行下一步阶数选择时只考虑k-1、k、k+1这三种情况,从中选择可以在下一步取最大步长的阶数.在该程序中,上述选阶原则是通过调整安全系数来实现的:
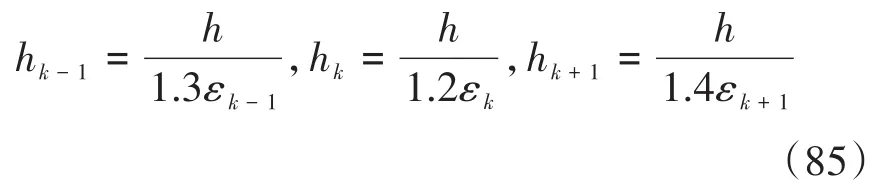

还要指出的是,如果变步长[53]或者变阶[54]算法不合适,也可能带来稳定性问题,因此通常步长和阶数不能增加得太快.作者经过测试发现,Gear等[53]给出的每一阶的最大步长增加量偏于保守,而Skelboe[13]给出的步长增加量在实践中更为合理,其步长增加上界fk如表1所示.

表1 BDF格式变步长的最大稳定增加量Table 1 The maximum stable increment of the variable step-size BDF format
高阶格式稳定性检测与自适应处理
不同阶数的BDF格式具有不同的稳定区域,其中只有前两阶是绝对稳定的,而更高阶的算法都在虚轴上有不稳定区域.在宽频动力学系统,特别是在含有柔性体或者大变形体的多体系统仿真中,某些频率可能会滑到这些不稳定区域内,造成误差的严重放大.此时上文的误差估计方法就不再正确,且阶数和步长选择策略也不再具有鲁棒性,在计算中表现为一种积分阶数的频繁跳跃现象,并伴随出现大量的积分步失败.为了避免这一问题,很多程序(例如LSODI[51])中建议手动设置最高阶数为2.为了进一步解决这一问题,实践中还发展出了几种其他解决方案:


表2 BDF高阶格式的失稳判断参数Table 2 Instability parameters of high-order BDF format

(3)Stewart[14]进一步考虑了步长变化的影响,提出当第n步结束时,如果下列条件满足:

则下一步暂时不考虑升阶,其中
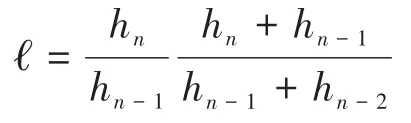
作者经过测试发现,将Skelboe和Stewart的方案结合起来,虽然最有效地克服了失稳问题,但在实践中似乎偏于保守,会影响计算效率.DASSL采用的策略虽然也可以在一定程度上避免失稳现象,但却不能保证不会出现失稳.其工作原理大致如下:如果x(t)至少k+1阶光滑可导,一般有

这是因为若系统可以用Taylor展开表达式逐阶近似,高阶Taylor项应当比低阶项更小.系统的数值光滑度可定义为选择最大的k满足如下条件


如果 x(t)达不到k阶光滑度,就不满足BDF算法的基本假设,只能采用 隐式积分器每步的计算量比较大,但其时间步长较大,总体来说计算效率较高;其稳定特性很好,可以很容易地处理方程组的刚性问题.但是,时间步长太大,可能会在计算中不能有效地处理局部的一些突变问题,而需要一些特殊的技巧. 在求解常微分方程(20)、(70)或者微分代数方程(32)、(38)、(78)和(84)的过程中,甚至在后文中显式积分器的约束流形投影过程中,都需要用到Newton迭代或者拟Newton迭代.动力学仿真中的非线性方程组的求解具有以下特点: (1)多.每个时间步都要用拟Newton迭代求解; (2)快.状态变量的预测值通常非常准确,往往只需2-3次拟Newton迭代即可收敛; (3)大.待求解方程组的规模比较大; (4)规.Jacobian矩阵往往具有特定的稀疏性. Jacobian矩阵的相关计算往往是整个仿真计算的瓶颈问题,这是由以下两个原因导致的: (1)Jacobian矩阵生成过程的计算量很大,无论是用解析表达式还是数值差分方法; (2)Jacobian矩阵的LU分解计算复杂度比其它计算过程要高,即使采用稀疏矩阵计算也是如此. 一般情况下多体动力学计算仿真中都用的是拟Newton迭代,以避免大量的Jacobian矩阵计算,并在所有地方都尽量复用Jacobian矩阵的LU分解.实践证明,这样做往往可以将计算速度提高5到10倍.还应该指出的是,几乎在所有的仿真过程中,总会遇到少数拟Newton迭代收敛很慢甚至失败的情形,给整个仿真带来问题.如果这些问题不解决,会导致整个计算的中止.而拟Newton迭代的失败,大多是由于Jacobian矩阵不再精确造成的.因此,为了解决这一问题,可以设一个最大迭代步数(例如4到5次),如果达到最大迭代步数还不收敛,就可以认为拟Newton迭代失败,需要重新生成Jacobian矩阵并继续进行迭代. 拟Newton迭代的一般过程为,为了求解非线性方程组F(x)=0,采用迭代格式 其中x*为真实解.该公式可以用来判断迭代是否收敛,因为右边项可以计算,其中σ可以由下式估计得出 为了保证拟Newton迭代快速收敛,需要监测收敛速度σ.计算中如果发现σ>0.9,最好重新计算Jacobian并估计σ.另外,实际计算中,条件(87)可能是不满足的,特别是在以下情形中: (2)强刚性问题中,Jacobian矩阵的条件数很大,近似Jacobian与真实Jacobian矩阵之间很小的差异,也会导致条件(87)不满足[31]; (3)在很多问题中,真实解析Jacobian矩阵的生成太过烦琐,或者其稀疏性不太好,往往用近似Jacobian计算,可能不满足条件(87); (4)在某些场合,非线性问题本身的收敛域可能很小,而这种情况是完全无法提前预知. 检测到拟Newton迭代不收敛时需要立即重新计算Jacobian矩阵,并进行LU分解.一般说来,拟Newton迭代的收敛速度低于Newton迭代,但计算量远小于后者.实际计算中需要结合二者的优点,尽可能地加快计算速度. 总体说来,广义 α方法计算步长较小,拟Newton方法的收敛性基本上可以保证;除非在某些情形,Jacobian矩阵接近奇异,或者出现某些不连续现象.而BDF族方法一般步长较大,因此拟Newton迭代不收敛,或者收敛速度太慢的问题也更加严重.作者建议如果在5步以内拟Newton迭代不收敛的话,最好重新计算Jacobian矩阵. 另一方面,由于一般动力学系统的质量矩阵、刚度矩阵和约束矩阵等随时间变化比较慢.因此,如果步长变化不大,上一步用到的Jacobian矩阵就可以在下一步被重复使用 .作者经过比较[8,56],建议采用如下判据:如果新步长与原步长相比, 则可以重复使用Jacobian矩阵,并采用松弛因子 最后,即使拟Newton迭代本身收敛,但得到的修正更新值也可能不满足预设的误差条件.总体说来,误差判断失败的原因可能有以下几点: (1)动力学中遇到非光滑事件(接触碰撞、机构奇点、参数或模型突变等),导致状态预测值不准确; (2)由于参数变化,用上一步仿真的后验误差估计得到的时间步长h太大,不满足误差限要求; (3)系统刚性太强,或者积分步长太小,导致Jacobian矩阵条件数很高,舍入误差太大. 其解决方案就是用得到的后验修正更新量重新设置迭代步长,并在必要的情况下降低积分器阶数.这一过程和变步长变阶策略类似,只是不会用到升阶,因而不用进行k+1阶的误差估计. 数值奇点是仿真中经常遇到的问题.与物理奇异点不同,数值奇点指的是因为数值原因导致的奇异位形,例如用欧拉角等参数描述旋转矩阵时遇到的奇点.数值奇异性的处理流程为: (1)奇点检测.对于每种可能遇到的奇异性都要设置接近于奇点处的报警功能; (2)奇点消除技术.选择新的坐标系统将数值奇点处的位形变换到新坐标系统下的非奇异位形; (3)积分器重启技术.在新的坐标下重启积分器. 数值奇点检测与处理的缺点在于随着部件数量的增加,不但自由度个数会增加,而且奇点出现的机率也会增加,而积分器重启的可能性也会增加.自由度个数增加,本来计算量就会增加;而积分器重启的机率也会增加,给仿真带来的效率损失也会增加.这种损失并非物理系统本身的特性导致,而是由于所选取坐标系统的数值特性不合适导致,只能用数值方法来解决. 数值奇点附近光滑性保持问题对于单步法比较简单的,例如对于广义 α方法,只要在奇点附近换一套局部非奇异坐标,换算出新坐标下的q、q̇、q̈和a就可以直接开始下一步的计算.积分步长只是局部发生了一些变化,而不会影响整体的仿真效果.而对于多步法,情况比较复杂.一种思路是总是从最低阶(1阶)用很小的步长重启并开始计算,其缺点是重启过程太慢,一般需要10-20步才能恢复正常仿真阶数和步长.对于很多部件组成的系统,奇点出现机会可能比较高,反复重启可能速度太慢,影响仿真效率.另一种思路是在奇点严重影响仿真效率之前,尽早进行坐标变换,并将前几步得到的结果也进行同样变换,保持高阶积分格式. 不光滑性出现一般有如下几个原因:接触碰撞、模型拓扑变化、不连续外力作用等等.其具体表现为某些物理量或者其时间导数、高阶导数的不连续性.不连续性问题在很多研究者看来似乎不甚重要,因为很多自适应步长的积分器往往可以通过多次试错突破不连续性的障碍,但其代价一般还是比较大的.好在对于绝大部分问题来说,不连续点的位置比较少,因此这些代价相当于整个计算成本来说还是比较小.但事实上,确实有不少工业界遇到的问题,是由于不连续性太强而求解失败.因此作为商业软件级别的积分器,还是应该包含不光滑性自动检测和定位的功能,从而可以保证更好的效率和鲁棒性.Gear等[57]提出一种ODE的不连续的检测和定位方法,可以用来将积分器的时间节点置于定位得到的不连续点,而不连续性问题可以有效地通过积分器重启得到解决.这一处理不连续性的方法也可以推广到DAE中去[58],并可利用以下性质: (1)质量矩阵M随时间的变化一般缓慢光滑,而外力项Q可能有一些不连续现象,而Q的不光滑性检测可以给下一步的预测提供信息; (2)除了在有限个间断点之外,约束C(q,ts)都是至少二阶连续.事实上,由于在所有计算过程中,都希望做到C≈0、Ċ≈0以及C̈≈0,因此不光滑性测试不能直接作用在它们上面,而选取实际中最关键的矩阵Cq中的非零元素作为不光滑性测试的量. 一般说来,显式积分器不适合用于求解代数微分动力学系统,但少数情形例外.在用递归方法得到的动力学方程组中,约束方程的个数远少于自由度个数;同时,如果系统的刚性问题不太严重,或者高频振动不能有效地得到衰减(例如对于大规模的接触碰撞问题的仿真),此时显式积分器的计算性能可能会优于隐式积分器.另外,显式积分器的计算量基本可控,因此比较适用于实时仿真.还有,由于显式积分器无需迭代,在多积分器合作仿真中实现起来方便得多. 约束修正法 从形式上看,约束修正法有些类似直接求解index-3的微分代数方程组.在这种意义下,大部分显式常微分方程积分器都可以用来求解方程组(1).首先,将方程组(1)改写成常微分方程组 其中γ和方程(5)中的一样.直接求解方程(88)会引起约束违约现象,因为公式(88)的第二个方程并不等价于公式(1)中的约束方程.方程(88)是常微分方程组,可以用高阶显式的常微分方程积分器来从tn时刻到tn+1时刻进行计算,所用积分器既可以是单步法又可以是多步法.计算得到的解不一定满足约束,因此需要进行修正,将每一步求得的q和q̇在约束流形上投影.显式积分器求解方程(88)的计算过程需要用到 在多体系统动力学中,由于M(q)和Cq(q,t)变化缓慢.因而J也是时间缓变的,可以采用各种近似和复用来提高计算效率.求解常微分方程的计算过程可以用算子在形式上表示为 和速度修正 这两种修正计算都需要通过迭代完成,计算中可以复用方程(89)中的J,以节省计算量. 罚函数法 形式上,罚函数法有些类似求解index-2的微分代数方程组(81),只是做了一些修改 罚函数的意思是利用很大的正数χ(罚因子)将index-2的微分代数方程组中的约束方程组 中形如f=0的约束改写成方程ḟ+χf=0的形式,得到 可以从中求解出q̇(q,v,t)和v̇(q,v,t),而且求解过程用到方程(89)中的J.得到的常微分方程组可以用显式积分器进行仿真,当然并非所有常微分方程积分器都适合开展罚函数法,有一类特殊的Runge-Kutta-Chebyshev类型的积分器[39-40],其在负半实轴上稳定域很长(见图1),因此适合用来显式求解方程组(91)和(92).本文推荐采用四阶的RKC积分器,其稳定区域是递归扩展的[40],且负半轴上稳定区域近似与递归阶的平方成正比. 图1 RKC积分器的稳定区域示意图Fig.1 Schematic of the Stable Domain for RKC Integrators 该积分器在虚轴上收敛区域有限,不适合用来求解刚性问题,但对一般非刚性的多刚体系统动力学递归格式,显式积分格式求解(91)和(92)的效果非常好.要指出的是,在计算之前可以从系统最大特征值基本确定罚因子χ,因为χ必须远远大于系统的最大特征值,进而可以定出递归阶.此外,提高计算效率的关键在于如何有效地从微分方程组(91)和(92)中求解出q̇和v̇,可以根据所求问题的特点加进这一过程. 一般来说,非完整约束的DAEs比完整约束的DAEs简单,因为对应的变量一般是index-2的.带非完整约束的DAEs的一般格式为[46] 该方程组可以分别被上面介绍的几种方法离散: (1)广义α族方法.同样假设q、q̇和q̈的表达式为方程(29)和(30),代入方程组(93),得到关于x、λ和μ的代数方程组 可以用Newton-Raphson方法或者其它迭代方法求解,其对应Jacobian矩阵为 (2)BDF族方法.将BDF方法的公式(74)、(75)和(77)代入方程组(93)得到离散格式 其对应Jacobian矩阵为 在求解出位置修正量δ后,可以计算出速度修正量ε;同样的,ε不能直接用来估计计算误差,而需要对几何约束作投影滤波修正. 带非完整约束的index-2格式的DAEs为 该方程组同样可以用广义α族方法和BDF族方法来进行积分,可以避免spikes现象,计算出更光滑更高精度的速度、加速度和约束力曲线. 此外,在实际应用中,多体动力学系统往往和控制算法结合起来应用,因此在仿真中也要将控制律方程组同时引入进行仿真.控制方程组往往由一阶微分方程组和代数方程组组成,因此可以通过一阶微分方程积分器,例如BDF方法等进行有效地时间离散.另外,动力学仿真中往往还包含一些离散动力学方程组,其积分方法大致有两种,一种是将离散系统连续化,另一种是交互仿真技术.前者比较简单,已经普遍应用于商业软件可以解决自适应步长与离散动力学时间节点的不协调问题;后者需要用到积分器与离散系统动力学之间的交互仿真技术,在本文中将不做赘述. 下面用两个典型多体系统动力学测试算例来说明文中讨论的一些技术细节.应该指出的是,不同族的积分器的局部误差估计在仿真精度控制实践中有着不同的意义,这既与积分器的阶数有关又与局部误差到全局误差的传导机制有关.仿真中的整体计算精度其实是由全局误差来控制,但全局误差很难估计.大量测试发现,广义α族积分器的局部相对误差限需要比BDF族积分器低两个数量级才能达到类似的整体仿真精度.例如在商业软件ADAMS中[59],HHT 积分器的缺省相对误差限为10-5,而BDF族积分器的对应误差限为10-3,才能保证二者的整体计算效果大致接近.在以下算例计算中,对广义 α族积分器,取局部相对误差限为10-6;而对BDF族积分器,取局部相对误差限为10-4.计算中,选择index-3的积分器作为广义 α族积分器中的代表;选择变步长公式的index-2和index-3格式的积分器作为BDF族积分器中的代表;而选择四阶显式积分器作为显式积分器族中的代表开展计算. 七刚体模型[60]是多刚体系统动力学的标准测试程序,其机构简图为图2.该机构与地面有四个连接点:点O位于原点;点A的坐标为(xA,yA);点B的坐标为(xB,yB);以及点C的坐标为(xC,yC).每个刚体的几何形状如图1所示,其质心坐标系用箭头标识出来;定常驱动力矩 τ作用于原点;C点连接的弹簧原长为 l0,其刚度系数为 k0.这些机构的几何参数及驱动力矩见表3,而每个刚体的惯性参数见表4. 表3 七刚体机构的参数Table 3 Parameters of the seven body mechanism 表4 七刚体机构的惯性参数表Table 4 Inertia parameters of the seven body mechanism 图2 七刚体机构系统Fig.2 Schematic of the seven body mechanism 上述模型分别用广义α积分器、显式积分器、BDF格式的index-3积分器进行仿真,其计算结果如图3所示. 图3 七刚体机构仿真中的曲线图Fig.3 Diagram for the simulations of the seven body mechanism 仿真过程中各种积分器自适应计算的步数和时间比较见表5.其结果显示,对于上述多刚体系统仿真来说,BDF积分器一般要比广义α积分器快;而对于非刚性问题,显式积分器也比广义α积分器快.这主要是由于七刚体模型满足高阶格式的连续性条件,可以采用大的时间步长进行积分.显式积分器基本不能用于一般的刚性问题求解,因为此时决定其积分步长的是稳定性而非精度,而此时稳定性条件导致显式积分器的步长非常小. 表5 七刚体机构仿真结果比较Table 5 The result comparison of the seven body mechanism 图4给出了计算中BDF积分器的阶数变化,证实了上述模型的仿真中,BDF积分器在整个计算过程中其自适应选择的格式阶数基本都高于二阶,这也是其可以采用大的时间步长来计算的主要原因. 图4 七刚体机构仿真中的BDF阶数曲线图Fig.4 BDF order profiles for the simulations of the Seven Body Mechanism 曲柄滑体机构模型是测试积分器性能的柔性多体系统动力学模型,因为实践表明,三阶以上的BDF积分器会在该模型中遇到稳定性的考验. 模型描述如图5所示,系统由刚性杆1、柔性杆2以及滑块3组成.刚性杆1的质量为0.36 kg,质心转动惯量为0.002727 kg∙m2,长度l1=0.15 m;柔性杆的密度为7570 kg/m3,截面为8×8 mm2的矩形,杨氏模量为200Gpa,未变形时长度0.30 m;滑块3的质量为0.7555 kg.忽略重力作用,假设给定旋转驱动为φ(t)=ωt,其中ω=150 rad/s.计算中取柔性杆前3阶横向振动模态和第1阶纵向振动模态的模态坐标来描述其变形.假设机构的初始位形为φ=0和x=0.45 m,以及横向振动模态坐标q1=q2=0,q3=1.033×10-5和纵向振动模态坐标q4=1.69×10-5;速度初始值由φ̇=ω可以由DAE初始条件分析算出其它广义初速度. 图5 曲柄-滑体机构系统Fig.5 Schematic of the crank slider mechanism 该模型具有很强的刚性,只能用隐式积分器来计算.用广义 α积分器、BDF格式的Index-2和Index-3积分器的计算结果如图6所示.从中可以看出,几个积分器的结果基本完全吻合;另外,直接求解index-3方程组得到的加速度曲线图中发生了误差放大的尖刺现象. 图6 曲柄滑体机构仿真中的曲线图Fig.6 Diagram for the simulations of the crank slider mechanism 由于BDF积分器里使用了自适应稳定性算法,在各阶频率组合导致高阶格式可能会发生不稳定性的场合,程序自适应地找到最合适的低阶格式(一般为二阶格式,如图7所示)来进行仿真,而无需手动修改设置,这样做为程序的使用带来了很大方便.另外,即使在如此不利的情况下,BDF积分器的计算效率也与广义 α方法大致接近,如表6所示,这也验证了BDF族积分器的高效性和鲁棒性. 表6 曲柄滑块机构用各种积分器仿真的效率比较Table 6 Comparison of simulation efficiency of various integrators for the crank slider mechanism 图7 曲柄滑块机构仿真中的BDF阶数曲线图Fig.7 BDF order profiles for the simulations of the crank slider mechanism 积分器的性能比较应该是在同样的计算精度下进行.在同样的误差要求下,index-2的DAE积分器的速度变量计算结果比index-3积分器的结果更准确;而且,index-2的DAE积分器可以解决index-3积分器在加速度和拉格朗日乘子曲线上的尖刺状误差.此外,index-1的DAE积分器计算得到的加速度曲线更光滑,而且可以对它们进行误差控制.其次从计算规模上来说,index-1的方程组规模大于index-2的方程组,更大于index-3的方程组;而其Jacobian矩阵的规模和复杂程度也是同样顺序.因此从计算效率上来说,index-3的DAE积分器大于index-2的DAE积分器,更大于index-1的DAE积分器.最后,从计算鲁棒性来说,大部分时候BDF族的index-2格式积分器优于index-3格式积分器;而index-3的广义 α积分器的鲁棒性似乎更佳. 从计算速度上来说,一般情况下认为在同样的精度要求下,BDF方法快于广义α方法.显式积分器不能求解强刚性问题,而根据目前的测试结果,它在弱刚性问题和一些中等刚性问题(刚性<104)的动力学仿真中比广义α方法要快.从程序设计角度来说,显式积分器最容易编程实现,因为无需迭代求解非线性方程组;广义α族积分器其次,而且稳定性比较好;BDF族积分器的结构最复杂,因为既需要实现变阶变步长,还要特别处理高阶格式的稳定性问题;特别是对于index-3的BDF族积分器还需要特殊处理速度变量的误差估计问题.从计算鲁棒性来说,显式积分器强于隐式积分器,而广义α方法优于BDF方法,因为大步长积分可能在连续性较差的问题中会引起计算失败.另外,广义α方法除了几个简单的参数调节以外,可以改进的地方很少,而BDF积分器中的Dk+2n+1矩阵所含信息量很大,如果能更好地利用可以有效提高其计算性能和稳定性.最后,显式积分器无需迭代求解大规模非线性方程组,在连续性较差的问题和并行仿真上应用潜力似乎更大. 就BDF方法的两种公式来说,一般认为,准定步长公式稍快于变步长公式,但由于后者直接采用原始数据而无需进行插值或者步长转换,在程序设计方便程度和鲁棒性方面优于前者.另外,广义 α方法的index-2格式尽管可以完全满足速度约束,但在很多实际问题应用中计算效率似乎不够高,值得进一步深入研究. 微分代数方程积分器是多体系统动力学软件的核心模块.在上世纪70至90年代,伴随多体系统动力学软件的开发热潮,积分器技术的发展进入了黄金时期.很多著名的研究团队,通过大量的理论分析和数值实验,提出了很多思路来解决动力学仿真中的各种数值问题.这些研究结果也大量被商业软件采用、验证和改进.同时,为了使自己的软件能更有效地求解各种工程问题,各大商业公司也投入成本,展开了大量的测试研究,从工程实践中提炼出了很多需求,并在软件升级中一一解决.目前可以认为,在比较有名的通用型软件中,传统单个积分器的技术已经比较成熟. 这几年,李群积分器和辛积分器的研究引起了很多学者的重视.李群积分器在求解高速旋转问题中有无与伦比的优势,其计算结果的精确性、算法的高效性和鲁棒性得到研究者们的赞赏.辛积分器在长时间仿真的应用中性能卓越.完善这些积分器的功能并开发出高效计算程序是目前正在开展的重要研究课题. 随着硬件技术的进步、计算规模的扩大和学科的交叉,多体系统动力学中的积分器技术也面临着新的挑战和机遇.积分器的计算复杂度一般在O(n2)与O(n4)之间,取决于系统的物理特性,其中n为系统的自由度.因此,积分器技术的一个重要研究方向是如何尽可能地降低通用型大规模多体动力学仿真中的计算复杂度. 本文讨论的都是动力学仿真中的初值问题.在最优控制的动力学系统仿真中,往往生成DAE的边值问题,即对某些状态变量,初始值给定;而对其它状态变量,最终值给定.一般多体系统动力学的边值问题要比初值问题复杂得多,其Newton迭代可能不收敛.发展适合大型多体系统动力学边值问题的积分器,也是需要重点研究的方向. 多物理场仿真目前来看是多体系统动力学的重点研究领域,而工业需求为积分器的研究提出了新的研究课题.如何将多体系统动力学中发展出来的积分器和其他学科的积分器整合起来求解多物理场问题,并要保证计算过程的精确性、高效性与鲁棒性,也是积分器技术的重要研究方向. 声明与致谢 多体系统动力学积分器的开发需要理论的指导,更需要详实的细节实现.在工作和学习中,作者阅读和研究过从Gear的DIFSUB到Petzold等人的DASPK等十几种ODE和DAE积分器的代码,从中受益非浅.本文主要以广义α族和BDF族积分器为对象,并结合作者实践中的一些体会,尽量系统化地介绍积分器程序开发中的一些关键技术.这些技术也可以用于其他族积分器的实现.作者声明,在本文内绝不包含任何非开源代码的技术细节,以尊重商业软件的专利和知识产权. 本文初稿完成后,北京理工大学胡海岩院士、清华大学任革学教授、青岛大学潘振宽教授、美国同事宋培林博士等阅读了相关内容,并给作者提出了宝贵的修改意见.作者深表感谢,也尽量按照几位前辈的意见作了相应的修改.作者在完成和修改本文过程中,曾就文中很多细节与北京理工大学刘铖研究员和哈工大魏承副教授反复交流讨论,最终才得以定稿,在此一并致谢.另外,还要感谢我的几个学生-杨凯、杨思铭、袁腾飞等,最初本文只是团队内部的简单讨论笔记,各位同学向作者指出了初稿中的一些含糊不清之处,进而帮助作者完善了本文中的一些细节内容.5 隐式积分器的其他计算细节
5.1 拟Newton迭代与Jacobian复用
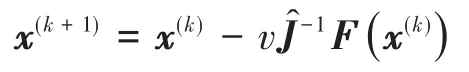
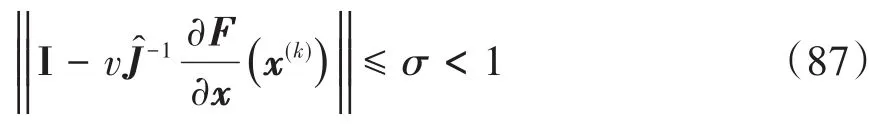


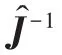


5.2 数值奇点检测与处理
5.3 不光滑性检测与处理
6 显式积分器简介

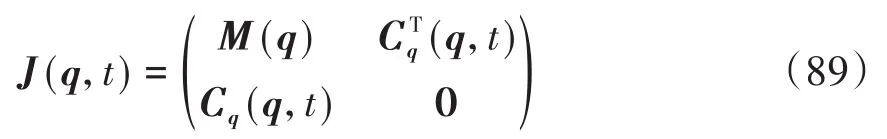

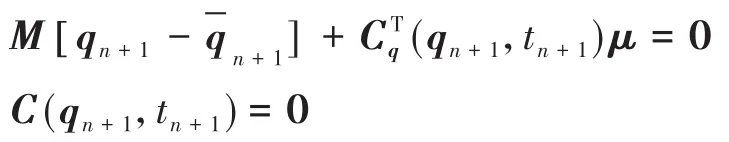
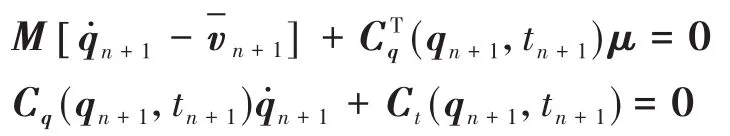

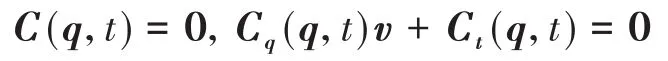


7 非完整约束DAEs的积分技术

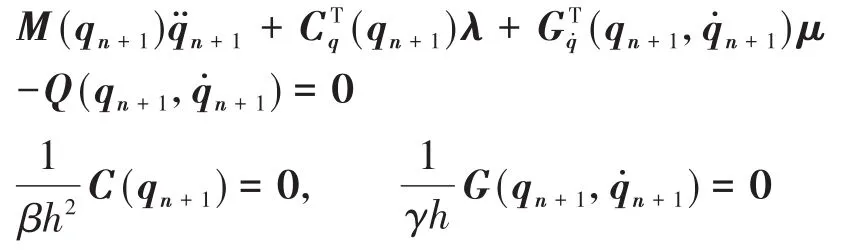




8 典型算例
8.1 七刚体机构
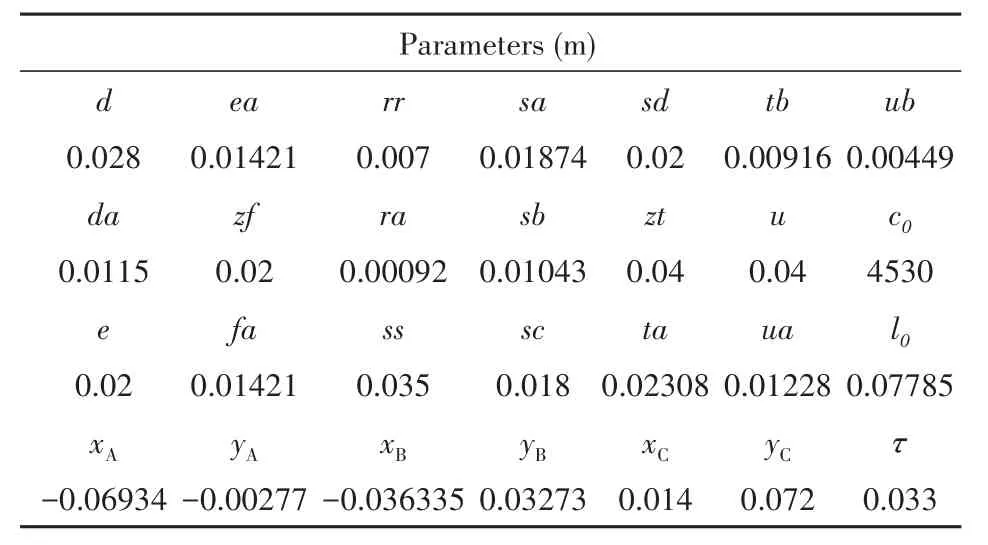


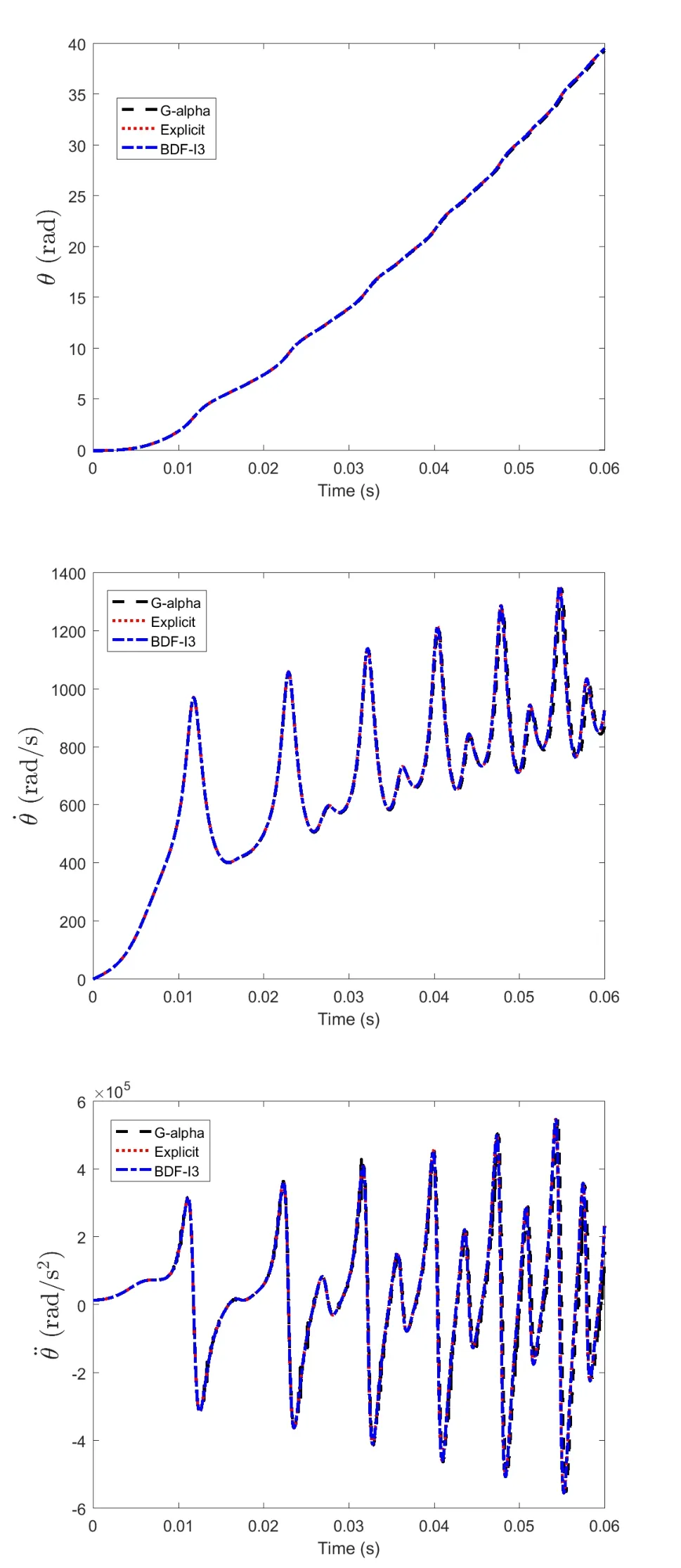


8.2 曲柄滑块机构
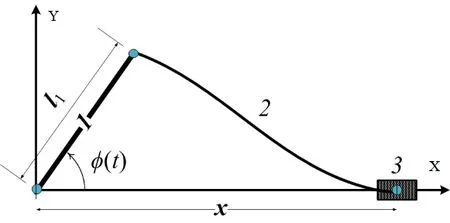



9 几种积分器的性能比较
10 展望
