用于感应式非接触励磁系统的CLC补偿拓扑研究
2021-05-19杨玉岗李朝
杨玉岗, 李朝
(辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125105)
0 引 言
为了保持最大功率输出强度,非接触电能传输系统通常采取原边恒流控制,副边则通常需要输出恒流或恒压来满足实际应用的要求。有研究者采用脉冲频率调制(pulse frequency modulation,PFM)或混合使用PFM和脉冲宽度调制技术,实现较大负载变化范围的恒流/恒压输出,然而工作频率的大范围变化会导致较大循环电流的产生和软开关特性的丢失,还可能导致频率分叉现象发生,使系统失去稳定性[5]。也有人通过级联DC-DC变换器来实现原边恒流输出和副边恒压输出,控制精度高,但电路结构复杂,增加了系统的成本,降低了效率和可靠性[10]。
文献[1]对复合补偿拓扑结构和特性进行了全面的研究;文献[2]总结了高低阶补偿搭配实现恒流或恒压输出的补偿拓扑;文献[3]总结了基于单个谐振电路实现恒流或恒压输出的各种补偿拓扑;文献[4]研究了产生负载无关输出电流的四种补偿方案;文献[5-7]研究了双边LCC和LCC/S补偿结构;文献[8-10]研究了双边LCL补偿拓扑;文献[11]研究了S/CLC(π型结构)补偿拓扑;文献[12]研究了四种传统低阶补偿拓扑的稳定性;文献[13]研究了原副边均用串联或并联补偿的几种结构及其品质因数;文献[14]研究了传统低阶补偿电路的电流、电压增益和电路功率因数;文献[15-16]研究了非接触励磁系统的变压器和补偿电路;文献[17-19]针对无线电能传输技术在不同场合的应用展开了研究。虽然双边LCL和LCC补偿电路都可以实现恒流输出和ZPA,但是这两者各自也都存在缺陷:双边LCL补偿电路有两个补偿电感,增大了系统的体积;LCC补偿电路参数设计受到限制,变压器自感必须大于补偿电感。S/CLC补偿电路在变压器副边的补偿元件较多,增大了体积,不便于用在副边电路需要旋转的场合。
本文提出一种新型的T型结构的CLC补偿拓扑,该结构能同时实现恒流输出和输入零阻抗角,利用电路本身的恒流特性简化了原边恒流控制的过程;输入零阻抗角特性能最小化输入视在功率,降低输入电源和开关元件的功率等级,且解决了传统串联-串联补偿感性区较深的问题,通过微调谐振参数易于实现开关管的ZVS。
1 CLC型补偿电路模型
图1为CLC补偿结构的原边等效电路,该补偿结构由补偿电容C1、C2和补偿电感L1构成;LP为松耦合变压器的原边自感值;Z为副边到原边的反映阻抗;Zi为输入阻抗,它们的模值分别为Z和Zi;UAB为补偿网络的输入电压;IP为流过变压器原边线圈的电流,后文中的UAB、IP均为有效值;UO为原边等效电路的输出电压。

图1 CLC补偿原边等效电路Fig.1 Primary equivalent circuit of CLC compensation
文中的分析过程都是建立在理想模型之上的,一般忽略寄生参数和谐波的影响。
1.1 恒流输出特性
设工作频率为ω,由基尔霍夫定律可求出:CLC补偿原边等效电路的输出电流为
(1)
若要使输出电流IP与负载阻抗无关,即与反映阻抗Z无关,只需要满足
(2)
即可。
因此,当CLC补偿电路满足式(2)的约束条件时,在全负载范围内输出恒定电流
IP=UABωC1。
(3)
由上式知,当工作频率确定时,可以通过调节补偿电容C1或者输入电压UAB(调节逆变桥移相角)来调节输出电流大小。
1.2 恒压输出特性
CLC补偿原边等效电路的输出电压为
UO=
(4)
若要使输出电压UO与负载阻抗无关,即与反映阻抗Z无关,只需要满足
(5)
即可。
因此,当CLC补偿电路满足式(5)的约束条件时,在全负载范围内输出恒定电压
(6)
由上式可知,此时电压增益与补偿电路参数和工作频率有关,当工作频率确定时,可以调节补偿电感、电容参数来调节电压增益。
1.3 ZPA特性
由基尔霍夫定律可求出CLC补偿电路的输入阻抗为
(7)
其中:
A=(ωL1)2Z,
(8)
(9)
(10)
输入相位角即输入阻抗角。假设副边电路完全补偿,若要使输入阻抗角为零,即输入阻抗Zi虚部为零,只需要满足下式即可:
(11)
因此,当副边电路完全补偿,CLC补偿电路满足式(11)的约束条件时,可实现在全负载范围内的输入阻抗角为零,此时的输入阻抗为纯电阻,即
(12)
综上所述,当补偿电路参数满足不同条件时,CLC补偿电路相应地表现出不同的电路特性。当CLC补偿电路满足式(11)的约束条件时,能同时呈现出恒流输出特性和ZPA特性。将这两大电路特性集于一身将非常有利于简化控制过程和减小无功输入,提高工作效率。
表1列出了CLC补偿电路满足不同参数条件时对应的电路特性。

表1 不同参数条件下CLC补偿电路的特性
对副边补偿电路经过类似的分析,可以得出:CLC补偿电路在满足几种不同的参数条件下也具有相应的电路特性。原副边补偿电路均可以使用CLC补偿结构,并可以根据实际需求进行原副边CLC电路不同特性的搭配以及与串、并联补偿的搭配。
2 感应式非接触励磁系统
感应式非接触电能传输系统的松耦合变压器按原副边的相对运动状态分为静止式、移动式和旋转式。其中,旋转式松耦合变压器通常应用在电机的励磁系统中,变压器的原边静止不动,副边绕轴旋转,原副边之间既无物理接触,也无电接触;取代了传统电机励磁系统中的电刷和滑环,解决了导线裸漏,电刷摩擦产生电火花,缩短工作寿命和降低工作的安全性和可靠性的问题[15-16]。
图2为感应式非接触励磁系统的结构模型,该系统主要由高频逆变电路、原副边补偿电路、松耦合变压器、高频整流电路和滤波电路几部分组成,将直流输入主要经过高频逆变、电磁耦合和高频整流之后得到直流输出送入励磁绕组中产生静磁场。
关于松耦合变压器,为了保证原副边相对旋转时磁场耦合不受较大影响,通常使用罐型变压器。松耦合变压器在大气隙的条件下进行非接触的功率传输,也因此导致原副边的漏感较大,会产生较大的无功功率,增加输入视在功率和环流损耗,因此需要在原副边分别增加补偿电路来抵消感性无功功率[15]。本文中设计的感应式非接触励磁系统用于电磁调速机的无线励磁。

图2 感应式非接触励磁系统Fig.2 Inductive contactless excitation system
2.1 感应式非接触励磁系统模型与电路结构
图3为感应式非接触励磁系统的电路结构图,其中,直流输入电压为Uin,逆变输出电压有效值为UAB,补偿网络输出电压有效值为Uab,直流输出电压为Uout,变压器原副边自感分别为LP、LS,变压器互感为M,负载电阻为RL。逆变电路为全桥电路,整流电路为不可控全桥整流电路,补偿电路为CLC-S(串联补偿简称S补偿)型补偿电路,副边具有恒压输出特性。将高阶补偿与低阶补偿相配合,既继承了高阶补偿电路的优良特性,又尽量减少补偿元件的个数,减小寄生参数的影响。
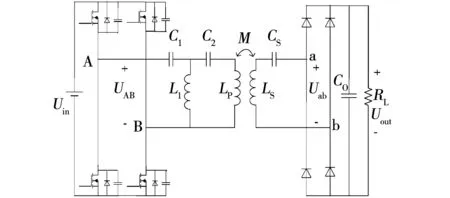
图3 感应式非接触励磁系统的电路结构图Fig.3 Circuit structure diagram of inductive contactless excitation system
2.2 谐振网络参数设计
原边采用CLC补偿,设谐振频率为ω0。由表1可知,为了使CLC电路既具有恒流输出特性,又具有输入零阻抗角特性,补偿参数应该满足
(13)
副边采用串联补偿,补偿参数应该满足
(14)
逆变输出电压有效值
(15)
交流等效阻抗
(16)
其中n为变压器变比。
直流电压增益为
(17)
3 系统的稳定性分析
系统的稳定运行是系统实现其他一切功能的前提条件,因此有必要对系统的稳定性进行研究。谐振频率普遍被认为是输入阻抗角为零时的频率,要保证系统的稳定性,就必须保证不同的负载条件下只有唯一的一个零输入阻抗角频率[12],即令输入阻抗虚部为零的解只有一个。
由式(7)可知,输入阻抗虚部
(18)
电路参数实际值与设计值的误差等因素可能导致系统运行的频率相对于谐振频率出现偏差。定义频率偏移系数γ=ω/ω0,表示系统工作频率偏离谐振频率的程度[12]。设电感比λ=L1/LP,原边绕组品质因数为QP=ω0LP/Z。令Im(Zi)=0,将γ代入式(18)中推导得
(19)
由式(19)可知,γ=1即副边侧谐振频率点必定是方程的解,要使得此解为唯一解,必须满足当γ≠1时,
γ2LP)=0
(20)
方程无解。
继续化简得
(21)
运用函数方法求解出γ=1为唯一解的条件为
(22)
式(22)的负载电阻表达形式为
(23)
故系统稳定运行的负载边界条件为式(22)或式(23)。
按表2中的参数代入式(7),利用MATLAB软件画出负载变化时输入阻抗角θ与频率偏移系数γ的关系曲线如图4。RL=33.75 Ω是由式(23)求出的使系统稳定运行的负载边界值。在边界值的两侧共取4组值为RL=10、20、40、50 Ω进行对比分析。
当负载电阻小于边界值时,在工作频率的变化过程中,系统只有一个输入阻抗角为零的频率点,验证了上述关于稳定性的理论的正确性。
当负载电阻等于边界值时,系统只有一个输入阻抗角为零的频率点。同时在谐振频率附近小范围内,输入阻抗角随工作频率变化的斜率很小,说明当系统带临界负载运行时,如果工作频率出现微小偏差,输入阻抗角随之产生的微小变化不会导致较大无功功率的产生,系统的工作状态几乎不受影响。

图4 阻抗角θ与频率偏移系数γ的关系曲线Fig.4 Relation curve between impedance angle and frequency shift coefficient
因此,若合理设计电路参数,使负载电阻小于但接近负载边界值,则不仅能使系统具有频率稳定性,还能包容由于电路元器件寄生参数和逆变、整流电路的非线性因素对工作频率造成的较小影响。
当负载电阻大于边界值时,在工作频率的变化过程中,系统会出现多个输入阻抗角为零的频率点,这会对系统的频率稳定控制造成很大干扰,系统可能无法稳定地工作在副边侧谐振频率点。
4 ZVS软开关的实现
因为CLC补偿拓扑具有ZPA特性,只要想办法调节电路参数让电路工作在较浅的感性区,便能够实现开关管的ZVS[6]。实现ZVS非常有利于提高电路的效率。文献[6]中提出了一种通过不对称处理T电路的方法来实现开关管ZVS。本文中的CLC补偿拓扑也可以采用此种方法,并且本文从中受到启发,探讨了单独调节某一个补偿元件参数来实现逆变器开关管ZVS的方法,最后对两种补偿方法进行对比分析。
1)不对称处理T电路的方法。
令X=ωL1,在不对称处理前,CLC补偿电路参数满足
(24)
进行不对称处理,令αX=1/(ωC1),βX=1/(ωC2)-ωLP,其中α、β分别是为了调节左、右桥臂参数而引入的系数。
可以推出输入阻抗
Zi=
(25)
进而得到输入阻抗角
(26)
根据公式(26)和表2中的参数,利用MATLAB画出输入阻抗角θ随处理系数α和β变化的3D曲面图如图5所示。从图5中可以看出,输入阻抗角θ随着左侧桥臂处理系数α的增大而减小,也就是说,为了使电路呈感性,应满足0<α<1,电容C1容值应该增大。另外,从图中取点α=0.98,β=1.96时,θ=17.09,说明右侧桥臂处理系数β的变化对输入相位角θ影响很小。同时,这也说明不对称处理T电路和单独调节电容C1容值实现ZVS,理论上都是可行的。

图5 输入阻抗角θ与处理系数α、β的关系曲面图Fig.5 A curved surface diagram of the relation between input phase angle θ and processing coefficients α and β
2)单独调节电容C1。
单独调节电容C1时,电路仍满足
(27)
推导出输入相位角θ与电容C1的关系如下:
(28)
根据式(28)和表2中的参数,利用MATLAB软件画出θ随电容C1变化的曲线图如图6。
图6说明输入阻抗角θ随着电容C1容值增大而增大,可以增大C1来实现ZVS,与方法1)中的结论是统一的。
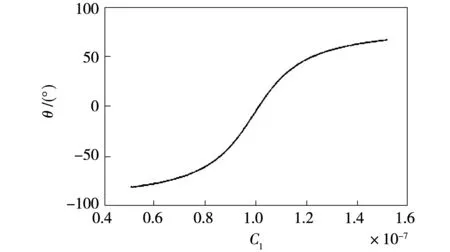
图6 输入阻抗角θ与电容C1的关系曲线Fig.6 Relation curve between input impedance angle θ and capacitance C1
图7为电容C1在设计值101.3 nF两侧取值时,通过saber电路仿真得到的UAB、IAB波形图。C1=86 nF时电流IAB超前于电压UAB,C1=103 nF时电压UAB超前于电流IAB,与图6中曲线变化趋势相符合,更直观地证明了调节电容C1容值产生的效果,与曲面图和曲线图从数学方法和电路理论的角度相互印证。
理论上,上述两种方法都能实现ZVS,但是,后者只调节一个参数,操作更加简单,而且对谐振工作状态影响更小。

图7 电容C1取不同值时的仿真波形图Fig.7 Simulation waveform of capacitor C1with different values
5 实验验证
根据电磁调速机的最大励磁电流1 A以及补偿电路仿真参数,制作了无线励磁系统的实验样机,图8为实验样机图片,表2为实验样机的参数。

图8 实验样机Fig.8 Experimental prototype
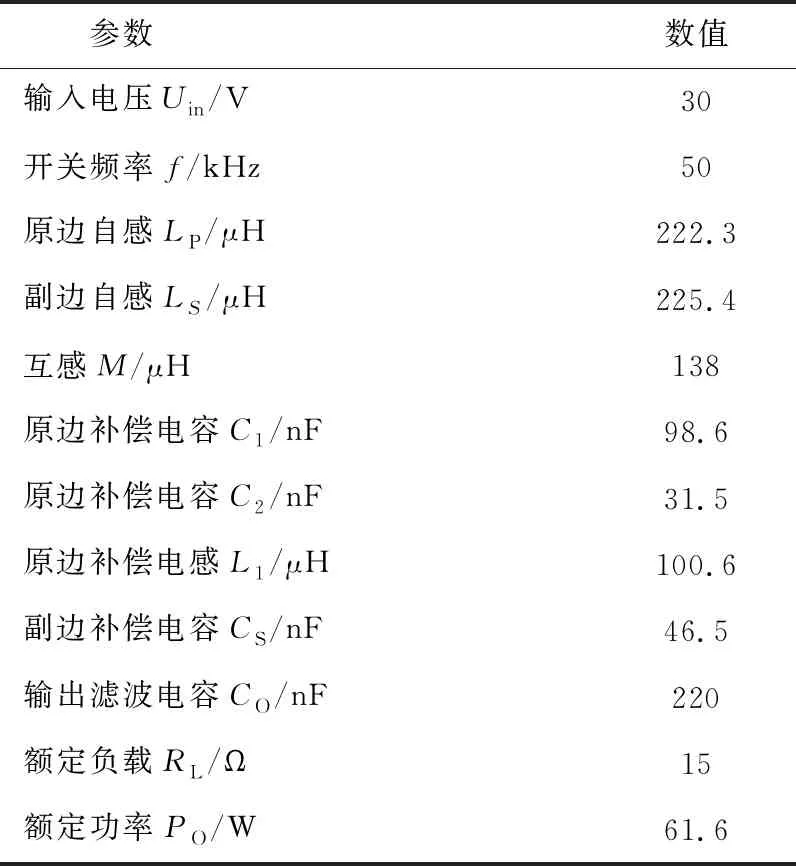
表2 样机参数
1)CLC型补偿拓扑的恒流特性测试。
改变负载电阻RL,并通过改变直流输入电压Uin来保持CLC补偿电路输入电压有效值UAB=28.5 V不变,检测CLC补偿电路输出电流IP有效值得到图9中的曲线,IP有效值基本保持在1.3 A左右,证明CLC补偿电路按2.2中的参数设计方法,具有与负载无关的恒流特性。

图9 恒流特性测试Fig.9 Constant current characteristic test
2)ZVS验证波形。
图10为开关管的Ugs、Uds波形图,图中开关管开通前Uds已经为零;图11为不同负载时逆变器输出电压UAB、电流IAB波形图,电压UAB稍微超前于电流IAB,二者都说明了电路工作在较浅的感性区,在负载范围内逆变器开关管实现了ZVS。仿真和实验研究发现补偿电容C1=98.6 nF时,电路工作在感性区,说明实际电路实现ZPA特性时的补偿电容C1取值略小于设计值。这种偏差主要与逆变桥和整流桥引入的谐波以及输出滤波电容有关,尽管理论与实验存在偏差,但是单独调节电容C1的方法仍对实现ZVS 时参数设计具有一定的指导作用[11]。

图10 Ugs、Uds波形Fig.10 Waveform of Ugs、Uds

图11 UAB、IAB波形Fig.11 Waveform of UAB、IAB
图12为负载电阻为15 Ω时,通过调节补偿电容C1实现ZPA特性时的逆变器输出电压UAB、电流IAB的波形图,此时电容值为88.5 nF。

图12 ZPA验证波形Fig.12 ZPA verification waveform
(3)效率曲线
由图13可知,负载电阻越大系统效率越高,但总体在80%以上,最大效率为85.3%。

图13 系统效率Fig.13 System efficiency
6 结 论
本文提出了一种新型的CLC补偿电路,该电路能同时实现恒流输出、ZPA。文中还基于CLC-S补偿电路,给出了补偿电路的参数设计方法,推导出了使系统频率稳定的负载边界条件,定量地讨论和比较了实现开关管ZVS的两种不同参数调制方法。仿真和实验的结果证明理论可以实现,CLC电路具有恒流特性;合理设计电路参数,让负载值始终小于负载边界值,能保持频率稳定;采用单独调节补偿电容C1的参数调节方法可以实现逆变器开关管的ZVS,实验的效率在80%以上。
