三相LCL并网逆变器自适应模型预测控制策略

谢运祥， 刘毓鑫， 关远鹏， 张峰

(华南理工大学 电力学院，广州 510640)

0 引 言

近年来，随着能源枯竭问题的日益严峻，分布式电源系统已成为国内外研究的焦点。电压源型并网逆变器能将直流电能高效地转化为交流电能，对于新能源和微网系统接入大电网极为重要。并网逆变器需要严格控制其注入电网的有功功率和无功功率，对于电流谐波的限制也十分严格。电压源逆变器需要通过低通滤波器与电网相连，LCL滤波器由于有更高的高频衰减特性，相比L滤波器能更好抑制入网电流谐波，因此被广泛应用。然而，LCL滤波器由于有着谐振尖峰问题，需要加入额外的谐振抑制策略[1-3]。

在过去十年中，模型预测控制(model predictive control,MPC)因其具有快的瞬态响应、易于实现、对非线性和约束直接处理的特点，被广泛应用于各种电力电子变换器中[4-16]。模型预测控制在LCL型换流器上的应用[4-7]也取得了丰富的成果。文献[4]提出LCL并网逆变器多步模型预测控制方法，将多个采样时刻的状态变量误差和开关状态变化量同时加入到价值函数中，起到状态变量跟踪和减小开关频率的作用。文献[5]提出了有源阻尼和模型预测控制相结合的控制方法，在保证模型预测控制的优良控制效果的前提下增加了系统的稳定性。文献[6-7]提出了PCi1i2uc控制策略，将逆变器侧电流、网侧电流、滤波电容电压加入到价值函数中，通过调整系数改变状态变量误差在价值函数中的权重，起到改善入网电流质量和有源阻尼的效果。但是有限控制集模型预测控制依赖于精确的模型参数，模型参数的误差会对有限控制集模型预测控制的可靠性造成影响[14-15]。

文献[14-16]指出模型参数误差会使得采用有限控制集模型预测控制的并网换流器输出电流产生畸变。电网呈现出的弱电网特性使得线路阻抗浮动[1]，并且电抗器饱和、温湿度变化也增加了模型参数的不确定性。为此，文献[16]提出一种多模块自适应控制方法，通过调整子模型的权重指标来获得系统全局近似模型，但此控制方法需要控制器建立数量庞大的固定的子模型，并且依赖于复杂的优化算法，给控制器的设计造成了困难。

为解决系统模型参数偏差，提高参数扰动情况下模型预测的准确性，本文提出一种三相LCL并网逆变器自适应模型预测控制方法。记录模型预测结果和实测系统状态，在每个参数调整时刻通过求解使得预测误差最小的系统参数，并将修正过的系统参数更新到系统离散状态方程中和状态变量参考值计算方程中。通过这种方法能使得系统参数得到周期性自适应修正，提高在弱电网下线路等效阻抗浮动和LCL滤波器参数扰动情况下模型预测的准确度。本文提出的方法对于弱电网导致的线路阻抗浮动和滤波器参数的扰动具有极强的适应能力，并且结合了有限控制集模型控制的优点，易于通过用DSP实施，通过实验验证具有较好的控制效果。

1 系统模型

(1)

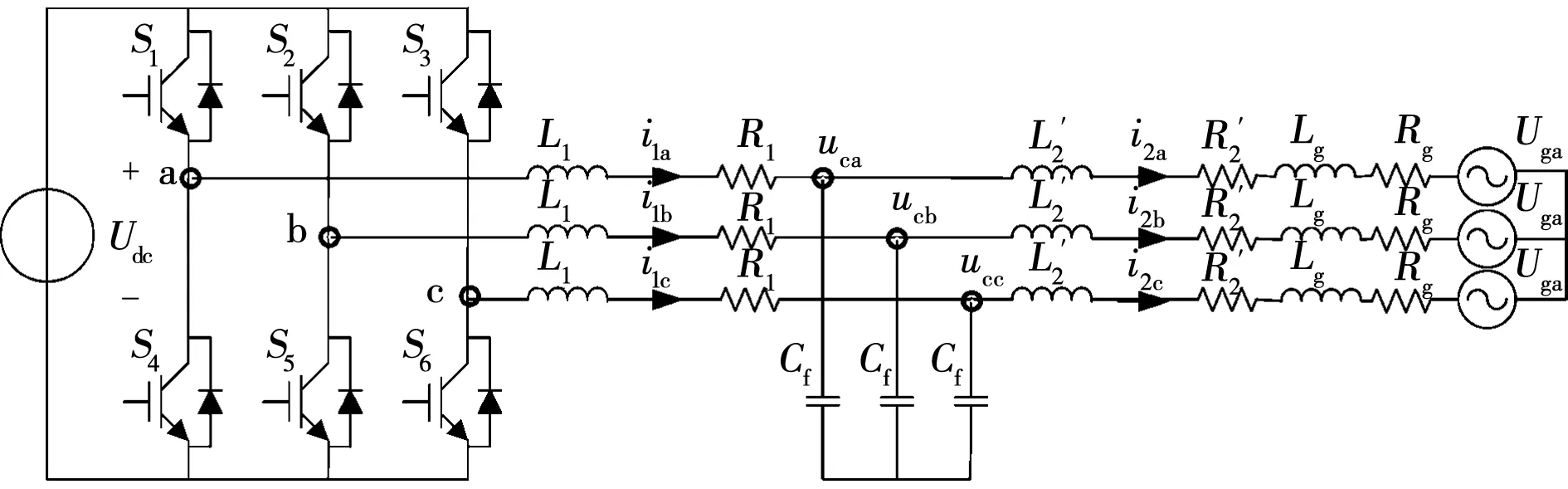
图1 LCL型并网逆变器拓扑图Fig.1 Topology of grid-connected inverter with LCL filter

当三相平衡时，其等效电路如图2所示，根据基尔霍夫电压定律可得：

(2)

其中：下标n=a,b,c代表着不同的物理坐标系；i1n是逆变器侧电感电流；ucn是滤波电容电压；i2k是并网侧电感电流；ugn是并网处电压。在方程中un为各桥臂开关状态决定的逆变器侧电压，表示为

un=Udc(Sn-0.5)。

(3)

其中：Udc为直流侧电压；Sn为各桥臂的开关状态：

(4)

图2 LCL型并网逆变器等效电路原理图Fig.2 Equivalent circuit diagram of grid-connected inverter with LCL filter

逆变器的三组桥臂在8种不同的开关组合下可以产生7种不同的电压矢量。在abc三相静止坐标系下的空间状态方程可以通过Clarke变换矩阵转化为αβ静止正交坐标系下的空间状态方程。在等幅值变换条件下，连续时间状态下，αβ静止正交坐标系下的空间状态方程可以表述以下方程：

(5)

其中状态变量是逆变器侧电感(L1)和并网电感(L2)的电流和滤波电容(Cf)电压在αβ 坐标系下的集合，x=[i1αi1βucαucβi2αi2β]T。输入变量向量为u=[uαuβ]T，且可表示为：

(6)

根据逆变电压的7种不同的电压矢量，u=[uαuβ]T有7种不同的组合：

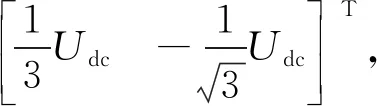
(7)

网处电压视为干扰向量w=[ugαugβ]T，状态矩阵、输入矩阵和干扰矩阵分别为

(8)

系统连续状态方程可精确离散化，转化为系统离散方程得

x(k+1)=Adx(k)+Bdu(k)+Edw(k)。

(9)

其中：

(10)

式(10)中的I为6阶单位矩阵，Ts为采样控制周期，式(9)意味着系统k+1时刻的状态x(k+1)可由k时候系统的状态x(k)、干扰量w(k)和系统输入u(k)决定。

2 基于模型预测控制的周期性参数调整方法

2.1 模型预测控制

系统离散状态方程可以被用作预测在每个可能的开关动作u=[uαuβ]T作用下系统下一时刻的状态。模型预测系统计算7种可能的开关状态下系统k+1时刻的系统状态x(k+1)(l)，在7种可能的开关状态中寻找使得价值函数值最小的一种开关状态u(l_opt)=[uα(l_opt)uβ(l_opt)]T,此开关状态作为最优解将在k到k+1时间段被应用。

文献[6-7]提出了PCi1i2uc的控制方法，此方法定义的价值函数为

g=w1{[i2αref(k+1)-i2α(k+1)]2+

[i2βref(k+1)-i2β(k+1)]2}+

w2{[ucαref(k+1)-ucα(k+1)]2+

[ucβref(k+1)-ucβ(k+1)]2}+

{[i1αref(k+1)-i1α(k+1)]2+

[i1βref(k+1)-i1β(k+1)]2}。

(11)

式中，各状态变量与参考值之间的误差均被加入到价值函数中，通过系数w1,w2来调整各状态变量的误差在价值函数中的权重。由此形式定义的价值函数不仅能使入网电流跟随参考值，还能有效地对LCL谐振进行抑制。加大w2的值可以增加LCL抑制程度，而增大w1的值可以改善并网电流质量。

2.2参考值的生成

并网逆变器系统的控制目标是注入电网的有功和无功功率，本文在PCi1i2uc控制方法的基础上提出一种状态变量参考值计算方法。

并网逆变器控制的精确性与电网电压幅值与相位密切相关。弱电网特性使得电网电压谐波增加，电压畸变严重[1,17]。文献[17]提出了通用二阶复矢量滤波器(SO-CVF)的同步旋转坐标系锁相环(SRF-PLL)策略。通用二阶复矢量滤波器在电网电压基波正序分量上的增益为1，且无相移，在电网电压基波负序分量处增益为0。因此该滤波器可以无失真地提取电网电压正序分量，消除负序分量对相位跟踪带来的影响。

通过SRF-PLL，在k采样时刻，可以准确地获取并网点电压幅值E(k)、角频率ω(k)和a轴电压相角θ(k)。

根据瞬时功率理论，在k+1时刻系统注入电网的有功Pout(k+1)和无功功率Qout(k+1)在dq旋转正交坐标系下可以表示为：

(13)

其中：ugd(k+1)、ugq(k+1)是k+1时刻电网电压通过等幅变换原则的Park变换得到的d轴、q轴分量；i2d(k+1)、i2q(k+1)是k+1时刻LCL型逆变器系统注入电网的电流通过等幅变换原则的Park变换得到的d轴、q轴分量。

在入网侧电压三相平衡的条件下，将同步旋转坐标dq的坐标系d轴定向于并网侧电压合成矢量上，q轴超前d轴90°可得：

(14)

由式(13)、式(14)可以根据有功无功参考Pref(k+1)、Qref(k+1)计算得到dq旋转正交坐标下的入网电流参考值分别为：

(15)

再根据坐标转换，将i2从dq静止正交坐标系下转换为αβ旋转正交坐标系，可得

(16)

由于电网电压幅值和角频率在一个采样周期内变化很小，可近似认为它们在一个采样周期内无变化，便可由k采样时刻电网电压幅值和相位估计k+1采样时刻电网电压幅值和相位，有：

(17)

由此可得k+1时刻电网电压在αβ旋转正交坐标下的值为：

(18)

由此可得k+1采样时刻在αβ旋转正交坐标下的入网电流参考值分别为：

(19)

由方程(2)可得：

(20)

在保证入网电流参考值为正弦函数时，由式(18)、式(19)、式(20)可得k+1采样时刻αβ坐标系下滤波电容电压参考值与逆变器侧电流参考值：

(21)

其中：

(22)

即通过计算b1、b2、b3、b4、b5、b6、b7、b8、b9、b10的值可得出k+1采样时刻αβ坐标系下电网侧电流参考值i2αref(k+1)、i2βref(k+1)，滤波电容电压参考值ucαref(k+1)、ucβref(k+1)，和逆变器侧电流参考值i1αref(k+1)、i1βref(k+1)。

2.3 周期性模型参数调整方法

模型预测控制需要通过精确的离散化系统模型对系统未来的状态进行预测，因此对于模型参数准确性十分敏感，不准确的电路参数将会导致对系统未来状态的预测造成偏差。由于弱电网特性，并网逆变器接入电网的线路阻抗将会浮动变化，并且温湿度变化、器件老化和电抗器饱和等因素会使得LCL滤波器电感、电容参数偏移设定值。

由于参数扰动，在对并网逆变器进行有限控制集模型预测控制时，在每个采样时刻系统状态变量的真实值会与预测值发生偏移。为能够动态得调整系统离散方程的参数，使得系统更加具有抗参数扰动的能力，增加控制系统的鲁棒性，本文提出一种自适应周期性参数调整的方法，以(k-m)Ts为周期动态地对系统参数进行更新。

由于系统方程中αβ轴的分量无耦合，由式(9)和式(10)中Ad、Bd、Cd可写为：

(23)

由系统离散方程可得：

(24)

假设每相电路上各原件具有相似特性，在同样的工作环境下具有相同的误差偏移，即参数发生改变后，电路仍保持三相平衡。

令hi1=[hi11hi12hi13hi14hi15]T，huc=[huc1huc2huc3huc4huc5]T，hi2=[hi21hi22hi23hi24hi25]T。

则在k采样时刻，逆变器侧电流误差ei1α(k)和ei1β(k)、电容电压误差eucα(k)和eucβ(k)、电网侧输出电流误差ei2α(k)和ei2β(k)可以表示为：

(25)

令：

(26)

ei1=[ei1α(m+1)ei1β(m+1)ei1α(m+2)

ei1β(m+2) …ei1α(k)ei1β(k)]T，

(27)

(28)

euc=[eucα(m+1)eucβ(m+1)eucα(m+2)

eucβ(m+2) …eucα(k)eucβ(k)]T，

(29)

(30)

ei2=[ei2α(m+1)ei2β(m+1)ei2α(m+2)

ei2β(m+2) …ei2α(k)ei2β(k)]T，

(31)

(32)

对于m+1采样时刻至k采样时刻的状态变量误差，可以表示为：

ei1=yi1-Fmkhi1，

(33)

euc=yuc-Fmkhuc，

(34)

ei2=yi2-Fmkhi2。

(35)

对于方程(33)，为使得在每个采样周期内的误差尽可能小，即使得如下方程取得最小值：

(36)

当k-m≥3时，即矩阵Fmk的行数大于列数时，可转为最小二乘估计问题，原方程可化为

(37)

(38)

则原式可化简为

(39)

其导数为

(40)

当式(40)取极小值时，有

(41)

可得

(42)

得到hi1的修正值为

(43)

同理可得huc和hi2的修正值为：

(44)

(45)

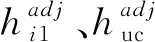
(46)

即

(47)

这样便可实现在(k-m)Ts周期(k-m≥3)对系统离散状态方程的参数进行调整。

另一方面有

(48)

在采样周期Ts足够小时，忽略Ts的高次项可得

(49)

由此可以解出第一电感、滤波电容、第二电感的参数修正值如式(50)所示，并将修正后的电路参数带入到式(21)、式(22)状态变量参考值计算过程中。

(50)

周期性模型参数调整策略实现的流程图如图3所示。有限控制集模型预测算法流程图如图4所示，整个控制系统的策略结构图如图5所示。

图3 周期性参数调整实现流程图Fig.3 Flow chart of realization of periodic parameter adjustment

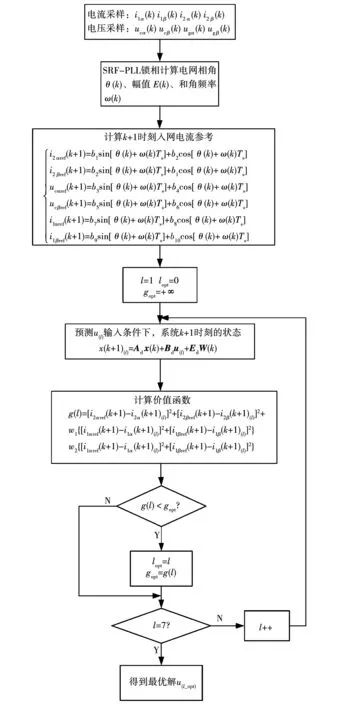
图4 有限控制集模型预测控制算法流程图Fig.4 Flow chart of finite control set model predictive control algorithm

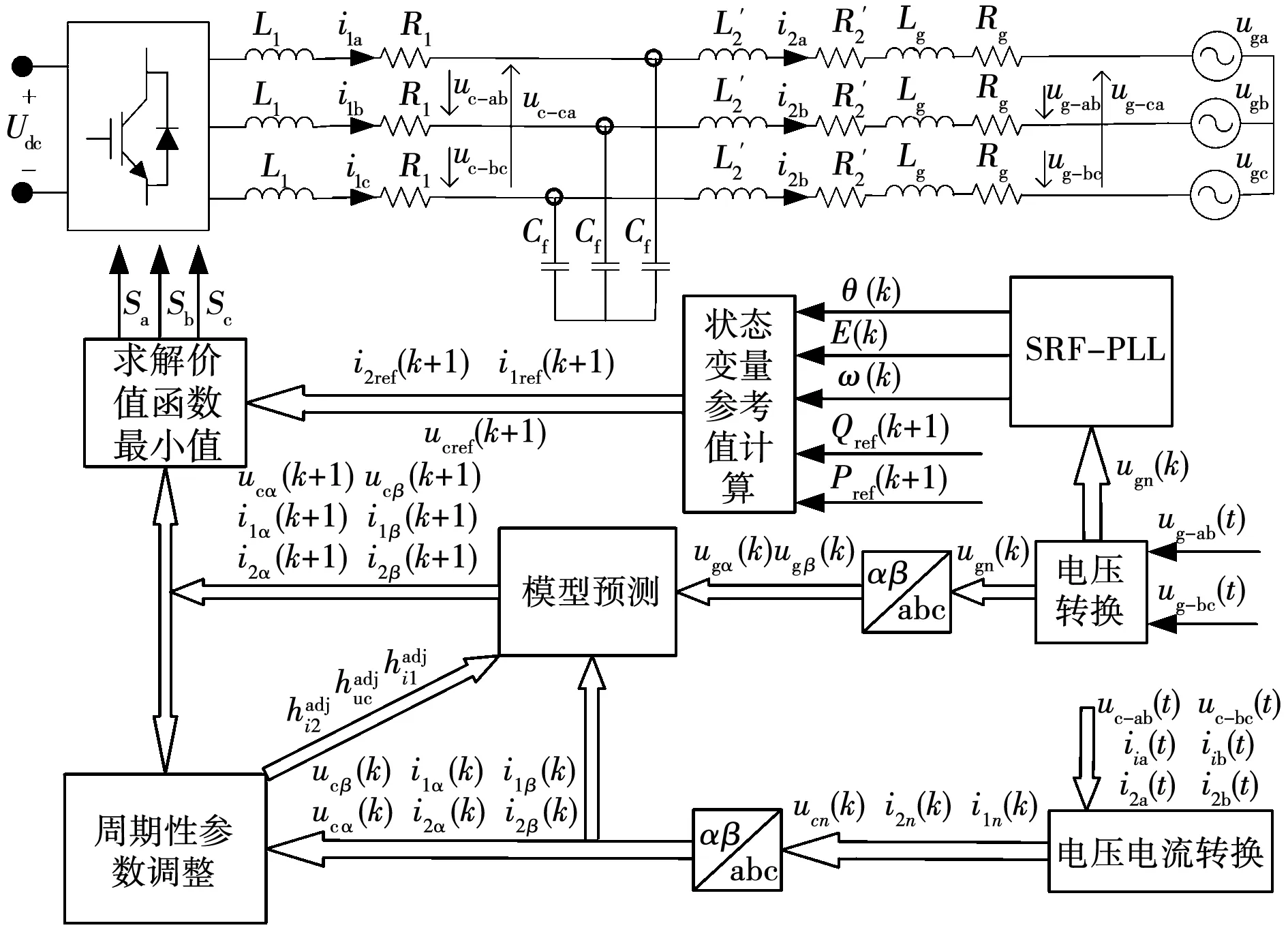
图5 总的控制系统策略结构图Fig.5 Overall control system structure diagram

3 实验验证

为验证本文提出的方法的控制性能，搭建了基于TMS320F28335控制芯片的3 kW三相LCL并网逆变器样机，样机照片如图6所示，实验平台参数如表1所示。其中可编程电网模拟器的型号为Chroma61845，可编程直流源型号为Chroma61604，示波器型号为Picoscope5444B。

图6 3 kW三相LCL并网逆变器样机Fig.6 Prototypeof 3 kW three-phase grid-connected inverter

本控制方法在无参数偏移情况下的稳态性能与动态性能将于传统的入网电流和电容电流双闭环控制对比，价值函数参数如表2所示，双闭环控制参数如表3所示。其中，表2所示的自适应模型预测控制参数和表3所示的双闭环控制参数皆为仿真调试优化所得。此外为验证本文提出的控制方法对于弱电网引起的参数波动和其他原因导致的参数偏移的适应性，将用未采取周期性参数调整的情况作为对照。

表1 LCL并网逆变器参数

表2 自适应模型预测控制参数

表3 双闭环控制参数

本文提出的控制方法与传统双闭环控制三相静态输出电流对比如图7所示，其中输出有功功率为2 kW，输出无功功率为0。本控制方法电流THD为2.31%。而传统双闭环控制的电流THD为2.82%。相比传统双闭环控制，本文提出的控制方法具有良好的静态性能。

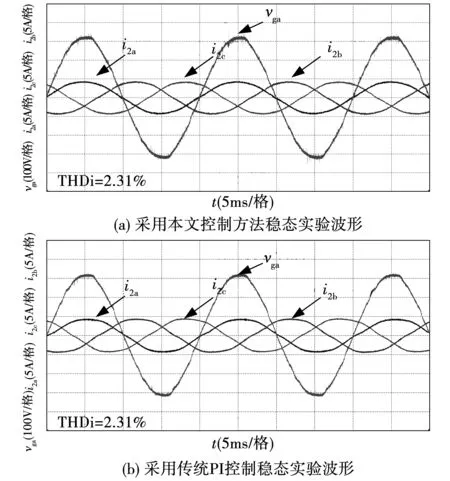
图7 静态输出电流对比图Fig.7 Static output current comparison diagram

本文提出的控制方法与传统双闭环控制三相输出电流动态对比图如图8和图9所示。图8(a)和图9(a)为输出有功功率由1.4 kW突增至2.8 kW三相电流波形动态波形图。图8(b)和图9(b)为输出有功功率由2.8 kW突减至1.4 kW三相电流动态波形图。由图8和图9可以看出，相比于传统双闭环PI控制，在本控制方法下超调量和调节时间均略微更小。由于本文未采取控制采样延迟和计算延迟的方法，在实际应用中，采样延迟和计算延迟会对模型预测控制的动态性能造成影响。

图8 本文控制方法电流动态波形Fig.8 Dynamic current waves of proposedadaptive MPC

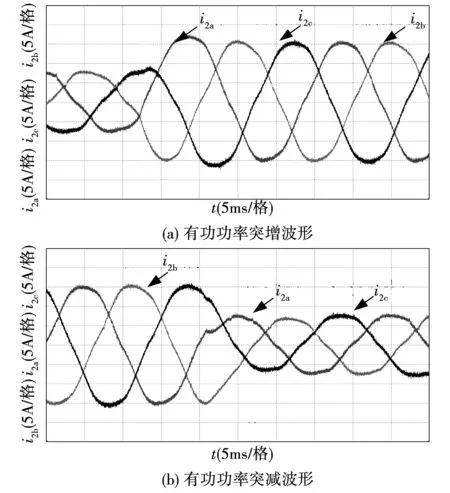
图9 传统PI控制动态电流波形Fig.9 Dynamic current waves of traditional PI control

图10为在不同线路电感偏差下，采用传统模型预测控制时三相电流输出波形。图11为在相应的线路阻抗偏差下，使用本文提出的周期性模型参数调整策略时的三相电流输出波形。表4给出对应的THD测试结果。

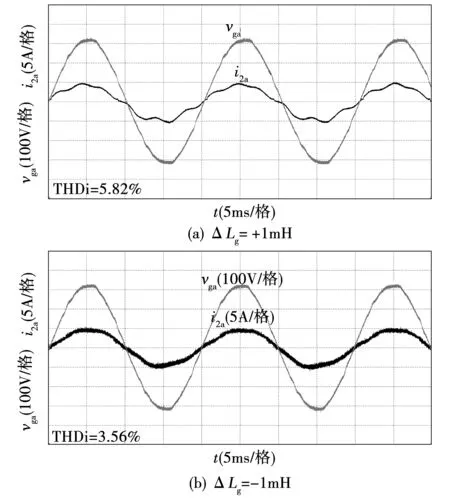
图10 线路等效电感偏差下传统MPC波形Fig.10 Traditional MPC waves with line equivalent inductance variation

图11 自适应MPC在线路等效电感偏移下波形Fig.11 Proposed adaptive MPC waves with line equivalent inductance variation

表4 线路电感偏移下并网电流测试结果

图12为在不同线路阻抗偏差下，未使用本文提出的自适应的周期性模型参数调整策略时的三相电流输出波形。图13为在相应的线路阻抗偏差下，使用本文提出的周期性模型参数调整策略时的三相电流输出波形。表5给出了其THD测试结果。

图12 线路等效电阻偏差下传统MPC波形Fig.12 Traditional MPC waves with line equivalent resistance variation

表5 线路电阻偏移下并网电流测试结果

由表4可得，当线路等效电感偏差为+1 mH时，使用本文所提模型误差消除策略后，逆变器输出电流的THD由5.82%降低为1.9%；当线路等效电感偏差为-1 mH时，使用本文所提模型误差消除策略后，逆变器输出电流的THD由3.56%降低为3.11%。由表5可得，当线路等效电阻偏差为+0.8 Ω时，使用本文所提模型误差消除策略后，逆变器输出电流的THD由3.27%降低为2.44%；当线路等效电阻偏差为+0.8 Ω时，使用本文所提模型误差消除策略后，逆变器输出电流的THD由2.68%降低为2.12%。因此，在模型参数失配情况下，采用传统模型预测控制会使得逆变器输出电流质量下降，在加入本文提出的自适应的周期性模型参数调整策略后，输出电流的质量可以得到明显提高。

图13 自适应MPC在线路等效电阻偏移下波形Fig.13 Proposed adaptive MPC waves with line equivalent resistance variation

4 结 论

本文基于三相LCL并网逆变器，研究了一种自适应模型预测控制策略。该控制策略继承了传统有限控制集模型预测的特点，采用最小二乘法精确识别系统模型参数，周期性地将修正过的参数更新到系统数学模型中。当线路阻抗浮动或滤波器参数变化时，逆变器能快速地修正模型参数，消除了模型状态预测不准确的问题。理论分析和实验结果都表明，相比传统的有限控制集模型预测控制方法，该控制策略具有以下优点：

1)更好的鲁棒性和抗干扰能力；

2)提高了并网逆变器对弱电网导致的线路阻抗浮动的适应能力；

3)提高了并网逆变器对温湿度变化、老化和电抗器饱和等因素导致的系统参数偏移的适应能力。