精密光机系统多敏感轴装配精度分析与装配工艺优化

吴 伟 邓 准 尚建忠 罗自荣 曹玉君

(1.国防科技大学智能科学学院， 长沙 410073； 2.北京遥感设备研究所， 北京 100854；3.湖南交通工程学院高科技研究院， 衡阳 421001)

0 引言

高性能精密光机系统已成为现代对地、空、海机动探测与制导装备中的核心部件，其设计和制造能力是衡量一个国家军事和科学技术水平的重要标志[1-3]。一直以来，这类光机系统的精密装配受到国内外众多学者、研究机构的关注[4-9]。作为一种复杂且高精度的精密光机产品，它包含多个敏感轴线，如光轴、惯导轴、机械轴等，这些敏感轴线之间的方向和位置精度对正确计算目标位置的影响极大，其匹配精度是影响精密光机系统控制性能(跟踪精度、稳定精度)的关键环节之一。确保各敏感轴之间的装配精度及装配效率对精密光机系统的装配一致性、性能稳定性及系统可靠性具有重要意义。

由于涉及领域的特殊性，关于精密光机系统多敏感轴装配的研究较少。李芳玲[10]针对某型航天器装配过程中光学舱与弹轴的匹配问题，设计了同轴工装，以保证二者的同轴度；YANG等[11]针对回转体对接中轴线对准问题，对圆柱形零件对接过程中的误差传播控制进行了深入研究；HUSSAIN等[12]研究了Straight-Build Assembly方法，基于刚体运动模型建立了装配过程的误差传播模型，并提出了3种优化方法，结果表明，通过优化可以使误差降低40%左右；在装配过程中，针对加工误差和装配误差在各个工序间的累积传播，SHIU等[13]基于关键产品特性和关键控制特性建立了装配过程的误差流模型，该模型考虑了产品几何尺寸误差，为多工位装配过程建模奠定了基础；WHITNEY等[14-15]将装配过程看作离散事件，采用状态转换方程表示该离散系统，研究了装配过程建模与控制理论的关系；杨勇等[16]提出一种基于结构整机性能映射模型的薄弱件结构优化方法，通过改进关键构件提升了整机性能；刘检华[17]针对航天器的装配提出了一种集精度、物理特性及结构件仿真分析一体化的虚拟装配过程建模与仿真方法。

目前，在精密光机系统的多敏感轴装配过程中大多采用直接对接法，该方法主要依赖于技师经验，装配一次性合格率较低，需要反复进行修配和调整，这严重制约了该类产品的装配质量和装配效率。本文以某型装备为研究对象，对多敏感轴装配精度进行建模分析，研究零件加工误差与轴线匹配精度的分布规律，通过调整装配策略和优化装配工艺，以期保证各轴线之间的装配精度指标。

1 问题描述与抽象

1.1 问题描述

某型装备采用异面共轴捷联布局，如图1所示，导引舱和惯导与弹体固连，二者安装面不同，但光学系统视线轴、惯导X轴与弹轴共线。这种布局方式能够有效减少弹体弹性振动引起的惯导轴与光轴转角的不一致性[18]。

如图2所示，理想情况下目标在惯性空间的视线角q0为

q0=δ+ψ

(1)

式中δ——理想弹体坐标系与基准系X轴夹角

ψ——理想光轴与理想弹体坐标系X轴夹角

在实际中，惯导和导引舱装配过程中会存在误差，惯导测量实际弹体坐标系(X′MY′MZ′M)偏离理想弹体坐标系(XMYMZM)，二者X轴夹角为Δδ；导引舱光轴实际测量坐标系(X′SY′SZ′S)也会偏离弹体坐标系，X轴偏离角为Δψ，此时，惯性空间下的目标视线角q为

q=q0+Δq=δ+ψ+Δδ+Δψ

(2)

可知，装配误差会引起附加视线角[19]。为了保证系统的性能，在对该类装备的装配过程中，必须保证光轴、惯导轴和弹轴的X轴互相平行，并且任意两轴之间的夹角在3′以内的指标要求。

1.2 问题抽象

弹轴X向定义为图1中基准面的法线；惯导轴X向定义为惯导4个减振座安装面最小二乘拟合面的法线；导引舱的光轴在装配时无法测量，装配时采用的也不是实际光轴，光学系统与伺服机构的对接面是光学系统的基准面，装配时将光轴等效为此面的法线方向，光学系统自身装调完毕后，通过研磨基准面以保证其法线精度。

多敏感轴装配相关部件的连接关系如图3所示，带箭头虚线表示二者存在X向角偏精度要求，实线表示二者对接，所有对接部件的X轴方向均为对接面法线。

所有部件均可简化为圆柱形舱体，舱体对称轴线为X方向，该多敏感轴装配精度问题就抽象为一系列舱段对接，保证其中若干舱体之间的角偏小于指标要求即可。

2 多敏感轴装配精度分析

2.1 角偏误差累积模型

在每个舱段上下表面均建立坐标系，坐标系原点位于回转轴上，当舱体不存在加工误差时，上下表面的坐标系X、Y、Z轴互相平行，如图4所示。

记某一舱体底面坐标系为F，顶面坐标系为F′。由于加工误差的存在，舱体顶面和底面不平行，F′与F的对应坐标轴不平行。F′相对于F的旋转误差定义为(Δα,Δβ,Δγ)，分别表示F′绕坐标系F的Y、Z、X轴的旋转角。由于只研究X向角偏，所以可令Δγ=0。由于坐标系原点位置可以任意指定，所以F′变换为F的变换矩阵[20]可简化为3×3的旋转变换矩阵，即

(3)

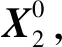
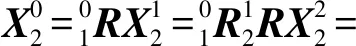
(4)

同理，当有n个零件对接时，矢量Xn在坐标系0中可表示为

(5)

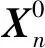
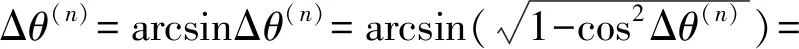
(6)

由于误差Δαi、Δβi远小于1,简化式(6)可得

(7)

因此，可知最终角偏误差Δθ(n)与每个对接舱段的加工误差(Δαi,Δβi)都有关系，第i步装配第i个零件而引入的误差会在装配的后续阶段中累积。但误差的累积并不一定是使角偏增大，若零件制造误差符号相异，也可能得到较小的角偏，即舱段对接面的加工误差之间存在补偿关系。因此，根据式(7)可知，当Δαi和Δβi的分布特征已知，可分析n个零件对接后角偏误差Δθ(n)的装配精度分布特征。当n=1时，有

(8)

式中 Δθ(1)——某个舱段上下端面的角偏误差

2.2 角偏误差分布规律

虽然加工误差Δα和Δβ与角偏误差Δθ有直接联系，但在设计和制造过程中并不直接对其提要求，而是规定舱段对接面的粗糙度、平面度以及相对于轴线的垂直度等形位公差。因此需要先根据装配特征的形位公差研究Δθ的分布特征，再得出Δα和Δβ的分布。

实际舱体的对接面凹凸不平，假设上下对接面最小二乘拟合平面的法向与参考轴的夹角分别为Δγ1和Δγ2，它们是二维矢量。舱体上下对接面之间的角偏误差为

Δθ=‖Δγ1+Δγ2‖

(9)

实际表面可看作不同频率成分轮廓的叠加，包括粗糙度轮廓、波纹度轮廓和形状误差[21]。粗糙度属于高频微观几何误差，波纹度是中频介于微观和宏观之间的几何误差，形状误差属于表面的低频宏观几何误差。舱段对接面采用磨削加工，波纹度幅值较小将其忽略，只考虑粗糙度和形状误差的影响。

为进一步简化问题，假设配合特征形状误差分量的波长远大于特征尺寸。根据假设，形状误差分量的作用相当于将粗糙度轮廓整体旋转一定角度。某型装备对接面粗糙度要求Ra=0.8 μm，平面度要求为0.01 mm。一般评价长度内最高波峰和最低峰谷之间的距离Ry≈8Ra=6.4 μm，可见零件平面度由粗糙度主导，形状误差中的短波长分量幅值很小，可忽略。

因此推出‖Δγ‖的计算过程为：首先生成零件表面的粗糙度轮廓，然后将其在垂直度限制下绕Y或Z轴旋转，最大的旋转角即为所求。

3D粗糙轮廓的生成方法已经比较成熟，包括Patir模型[22]、FFT法[23]、时间序列型[24]和分形模型[25]等，本文采用Patir模型生成3D粗糙轮廓，图5为数值模拟粗糙度Ra=0.8 μm的粗糙表面。

为了验证粗糙表面生成的有效性，对比仿真表面与实测表面的平面度。实际测量了33个对接面样本的平面度；运行粗糙表面生成程序2 000次，并计算仿真表面平面度，其结果如图6所示。图6a为根据粗糙表面生成程序得到表面的平面度，图中曲线为正态分布N(0.004 7,0.000 4)；图6b为实测表面平面度，图中曲线为正态分布N(0.004 6,0.001 6)。显然，仿真表面与真实表面平面度具有相似的分布规律，但是由于实际表面在加工中受到更多因素的影响，因此其平面度的分布更加分散。

根据前面分析可知，叠加形状误差的过程相当于在垂直度的限制下对粗糙度轮廓绕Y轴或Z轴进行最大程度的旋转，旋转角为‖Δγ‖。零件垂直度的实际值为随机变量，设上下对接面参考面位置分别为x1和x2，则垂直度p为

p=|x1-x2|

(10)

假设x1和x2服从正态分布x1～N(μ1,σ1)，x2～N(μ2,σ2)，则垂直度p符合折叠正态分布，其概率密度函数为

(11)

绘制实测的53个对接面的垂直度数据样本的分布，如图7所示，图中曲线为折叠正态分布FN(0.015,0.006)。

依据图7概率密度函数，随机生成垂直度，然后对粗糙度轮廓绕Y轴进行最大程度旋转，得到‖Δγ‖分布规律如图8所示，它符合广义极值分布。在垂直度范围内，粗糙度轮廓可能的旋转角是随机的，而‖Δγ‖正是这个随机样本中的极大值，所以它符合极值分布，有

‖Δγ‖～GEV(μGEV=0.315 4,σGEV=0.197 3,ξGEV=-0.211 5)

(12)

式中μGEV——定位参数σGEV——尺度参数

ξGEV——形状参数

如图9所示，Δγ1和Δγ2是二维矢量，可以将其分解为绕Y轴转动和绕Z轴转动，根据式(9)可得

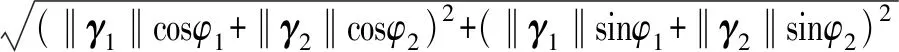
(13)

φ1和φ2符合0～2π内的均匀分布，对式(13)进行蒙特卡洛仿真，绘制仿真结果分布如图10所示，分析得到Δθ符合莱斯(Rice)分布，即

Δθ～Rice(vR=0,σR=0.441 6)

(14)

莱斯分布概率密度函数为

(15)

式中I0——修正的0阶第一类贝塞尔函数

假设Δα和Δβ独立同分布，则根据式(8)以及莱斯分布的定义可知Δα和Δβ符合均值为0，标准差为σR的正态分布N(0,σR)。

通过上述仿真和分析，得到舱体对接面的加工误差Δα和Δβ符合正态分布，舱体上下表面之间的角偏误差Δθ符合莱斯分布。

3 基于装配方向调整的逐工序优化法

针对多舱段装配问题，将n个舱段对接过程分为n个工序，每个工序对接一个舱段。为了提高装配精度，每个工序都应该对角偏进行控制，控制方法不同，最终得到的装配精度也不同。对于回转对称舱段，设每个对接面有k个螺栓连接孔，在装配过程中可以将舱段绕其回转轴旋转，从而每个舱段拥有k个可能的装配方向。

3.1 直接对接法

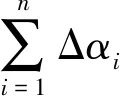
(16)

角偏均值(Mean)和标准差(Standard deviation, SD)分别为

(17)

(18)

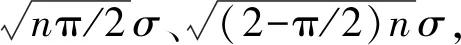
3.2 逐工序优化装配方向法

根据多舱段的装配特点，提出了基于装配方向调整的逐工序优化法。 这种方法的本质是在每个工序(Stage)中都尽量使角偏误差Δθ(i)最小，第i个工序最优化的方法是将舱段i绕其回转轴旋转，在k个可行的装配方向中选取使Δθ(i)最小的方向进行装配。因此，工序i最终的角偏误差Δθ(i)为

(19)

显然Δθ(i)服从GEV分布，其母分布为Rice分布。

当舱段螺钉孔个数k=6时，角偏的分布参数μGEV、σGEV、ξGEV与舱段加工误差分布参数μN、σN的关系如图11所示。由图11可知，当σN≥0.7μN时，角偏的分布参数几乎不随工序发生改变(除工序为2时)。即当制造误差满足σN≥0.7μN，n个(n>2)零件对接，都将得到几乎相同的角偏分布；当σN<0.7μN时，角偏的分布参数随工序发生波动。而且定位参数μGEV和尺度参数σGEV都是当工序为偶数时较工序为奇数时小。所以偶数个零件对接会比奇数个零件对接的角偏精度高。

采用这种装配方法需要对现有加工和装配工序进行优化调整，优化后装配工艺路线如图12所示。

制导舱和动力舱完成端面精加工后，暂不执行其他加工工序，直接进入装配工序。光学系统与伺服机构有方向要求，二者直接对接；惯导与安装板之间可通过减振座预紧力调整角偏，二者也直接对接；然后将导引舱组合与制导舱对接，通过调整制导舱方向，最小化导引舱与制导舱之间的角偏。将惯导组合对接至制导舱，惯导与导引舱也有方向要求，通过调整减振座预紧力最小化惯导与导引舱角偏。将动力舱对接至制导舱，通过调整动力舱方向最小化导引舱与弹轴角偏。标记各组合装配方向，拆卸，然后完成制导舱和动力舱的剩余加工工序，最后按照标记的方向将各舱重新装配。

4 案例装配分析

采用仿真的方法对两种对接方法进行对比分析，输入的零件舱段分布数据分为两组案例，如表1所示。

表1 舱段的分布参数Tab.1 Distribution parameters of cabin

案例1是实测了40个舱段的上下端面的角偏Δθ，得到其分布为Rice(0.1,0.7)，Δα和Δβ的分布为N(0.070 7,0.7)，因为实际舱段在加工过程中存在夹具误差，所以Δα和Δβ的均值不为0；案例2中Δα和Δβ分别赋值为N(1,0.418 8)，则有Δθ～Rice(1.414,0.418 8)。

使用上述两种方法分别对两个案例进行装配，二者均包括8个舱段、6个螺钉孔，分为8个工序进行装配，不考虑装配过程中的定位误差和测量误差，每个装配实例仿真10 000次。

图13为采用直接对接法的仿真结果。由图可知，角偏均值、标准差随工序增大而增加。舱段加工误差μN越大，则角偏均值增长速度越大；σN越大，角偏标准差增长速度越大。案例1中8个舱段对接后，角偏增大203.3%；案例2中8个舱段对接后角偏增大673.9%。

图14为采用逐工序优化装配方向法的仿真结果。由图可知，案例1与案例2角偏均值呈现出不同的特征，案例1对接后(工序大于1)角偏均值基本保持不变；案例2角偏均值则表现明显的振荡，工序为奇数时角偏均值处于波峰，当工序为偶数时角偏均值处于波谷，并随着工序的增加逐渐收敛。相同的特征也体现在标准差上。因为案例1中σN≥0.7μN，角偏分布参数基本不随工序变化；而案例2中σN<0.7μN，角偏的分布参数随工序有规律的波动。装配后角偏明显小于单个舱段的角偏，零件角偏越大，装配后角偏也越大。案例1标准差小于案例2标准差，说明装配后角偏标准差不仅与加工误差标准差有关，还与加工误差均值有关。

图15为采用两种方法对接装配时，不同工序角偏的概率密度分布图。由图15a可知，加工质量、对接舱段个数对直接对接法装配精度的影响都很大，不利于多段舱体对接装配，角偏随舱体个数增加而增加，且加工精度越低增速越大。如果以3′为指标，一次性装配合格率要求大于95%时，那么案例1对接零件个数不能超过3个，而案例2几乎无法达到合格率要求。某型装备舱体对接采用直接对接法，因为舱体对接前，内部设备已经安装到位，设备具有方向性，致使舱体在对接时已经无法调整方向。正因如此，其装配一次合格率非常低，经常要“测试-拆卸-修配-装配-测试”6～8次，甚至出现过反复20余次的极端情况。

由图15b可知，逐工序优化装配方向法对舱段加工误差具有较明显的补偿能力，对接舱体个数的增加对降低最终角偏并无明显作用。案例1中8个舱体对接的角偏相对于2个舱体对接的角偏仅下降3%。案例2中对接舱体达到4个后，角偏波动趋于平稳，8个舱体对接角偏相对于4个舱体对接角偏变动5%，并且两个案例装配后角偏小于3′的概率大于99.8%。

5 结束语

以某型装备为研究对象，分析了光轴、惯导轴与机械轴等多敏感轴之间的装配精度。通过研究该类装备的装配结构特点，将多敏感轴精度装配问题抽象为舱段对接过程中的角偏精度问题，基于坐标变换建立了多敏感轴装配过程的角偏误差累积模型，提出基于粗糙表面研究不同对接方法下角偏概率分布的方法，分别对采用传统的直接对接法和所提出的逐工序优化装配方向法下的角偏概率分布规律进行了研究，并对两个设计案例进行了仿真。研究表明，采用直接对接法时，舱段加工误差在装配过程中累积显著，难以满足各轴线之间3′的装配精度指标要求，也揭示了当前装配一次性合格率较低的原因。而逐工序优化装配方向法能够在较大程度上补偿舱段的加工误差，并对当前的精密装配工艺进行优化，该方法能够有效保证各敏感轴线之间的装配精度，且装配精度几乎不受对接舱段个数的影响。