基于有限位置法的冲压机构摆动力完全平衡设计

沈惠平 聂亚彪 李 菊 杨廷力

(常州大学现代机构学研究中心， 常州 213016)

0 引言

实现摆动力和摆动力矩平衡是高速机构设计必须考虑的问题。国内外学者提出了机构摆动力和摆动力矩完全平衡的一些理论和研究方法[1-7]。

BERKOF等[8]提出了线性独立矢量法，并给出了一般平面机构摆动力完全平衡条件的求解步骤；文献[9]提出了质量静替代法，通过对机构各杆件质量的重新分配，实现了一平面四杆机构的摆动力完全平衡；BAGCI[10]通过在机构中附加杆组或子机构的方法，实现了对某些特殊机构的摆动力平衡；文献[11-12]提出了质量矩替代法，通过将机构中所有连枝构件的质量矩均转换为与之相邻的树枝构件的质量矩，推导了所有树枝构件摆动力平衡条件；BRIOT等[13]提出一种基于机构总质心最优控制的方法，求解了高速机械手的摆动力平衡问题，并通过对不同运动轨迹的数值模拟，验证了该方法的有效性；OUYANG等[14-15]提出一种通过调整机构运动学参数使机构总质心静止不动的方法，从而实现其摆动力的完全平衡。CHAUDHARY等[16]以机构摆动力和摆动力矩为目标函数，基于遗传进化算法(GA)得到了一组最优解，并验证了该解的有效性；GENG等[17]在不增加机构整体质量的前提下，通过优化机构总质心轨迹，使机构达到了较好的摆动力平衡效果。上述摆动力完全平衡的方法几乎都是基于解析法导出机构平衡条件，以适应机构运动的任意位置。而有限位置法[18-20]的思路是：如机构在有限个位置(一般为v+f+1，v为独立回路数，f为自由度)上摆动力完全平衡，则机构在任意位置上的摆动力也一定完全平衡。

本文应用有限位置法对降耦优化得到的一种含3个回路的零耦合度平面高速冲压机构进行摆动力完全平衡设计与分析。

1 拓扑结构分析及树系统划分

1.1 拓扑结构分析

图1为零耦合度(κ=0)平面八杆冲压机构，是针对文献[21]中耦合度κ=1的平面八杆冲压机构(只能求得数值型位置正解)，根据机构拓扑降耦设计方法[22-24]进行拓扑优化设计得到的。

该高速冲压机构主要由驱动构件1和3个平面Ⅱ级杆组(2、3)、(4、5)、(6、7)组成，其中，机架为0，移动副P1为主冲压头，移动副P2为辅助推料器，其余7个关节(A～G)均为转动副。机构中每一构件都存在一条只由转动副组成的通路，满足通路定理[15]，因此，该机构可用配重法实现摆动力完全平衡。

显然，该机构包含3个独立回路，每个回路的独立位移方程数ξLi=3(i=1，2，3)，根据全周自由度公式[25]可得

因此，机构仅需一个原动件，当冲压机头P1向下冲压时，辅助推料器P2完成自左向右的冲压料自动推送，从而完成冲压，保证了操作人员人身安全。

3个回路A-B-C(P1)、F-E-D、E-G-P2的约束度分别为

因此，上述3个回路分别构成3个子运动链(SKC)，分别为SKC1、SKC2、SKC3，它们耦合度[25]分别为

因机构耦合度为零，机构具有解析式位置正解。

1.2 树系统划分

因每个SKC可看作一个完整的树系统，根据连枝构件选取原则，可将每个SKC的构件进行划分。

SKC1: A-B-C(P1)中，选取构件3为连枝构件，构件1、2为树枝构件。

SKC2: F-E-D中，选取构件5为连枝构件，构件4为树枝构件。

SKC3: E-G-P2中，选取构件7为连枝构件，构件6为树枝构件。

由图1可知，树枝构件4、6与连枝构件5通过一个复合铰链RE连接，因此，树枝构件6和连枝构件7又可看作树枝构件4的子树系统。

2 位置分析与验证

应用有限位置法进行机构摆动力完全平衡计算时，需要对机构进行位置分析，故将图2机构在SolidWorks中建立三维模型。

2.1 参数设置

杆件长度：lAB=l1=40 mm，lBC=l2=113.14 mm，lDE=l3=170 mm，lEF=l4=109 mm，lEG=l5=109 mm。机架长度：lm=235 mm，ln=205 mm。

设平衡前各杆为质量均匀分布，即除三副杆2之外，其余各杆质心都位于其连杆直线上，即质心参数qi(i=1,3，4，…，7)均为零。

由建立的SolidWorks模型可知，各杆件其他质心位置参数为p1=20 mm，p2=56.83 mm，q2=11.59 mm，p3=0，p4=48 mm，p5=79 mm，p6=48 mm，p7=0。各杆件质量为m1=0.001 kg，m2=0.007 kg，m3=0.006 kg，m4=0.003 kg，m5=0.004 kg，m6=0.003 kg，m7=0.006 kg。其他参数：三副杆2为等腰直角(α=45°)，且lBC=lCD=80 mm，θ3表示构件3与机架的夹角，恒为90°；θ7表示构件7与机架的夹角，恒为0°，未在图中标出。

2.2 位置参数求解

由图2可知，点A、B、C、E、G坐标为A=(lm，ln)、B=(lm+l1cosθ1，ln+l1sinθ1)、C=(lm，By-l2sinθ2)、E=(Fx+l4cosθ4，Fy+l4sinθ4)、G=(2l4cosθ4，0)。

已知θ1为驱动角，易求得构件2、4、5、6的角位置θ2、θ4、θ5、θ6分别为

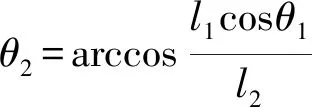
其中

利用Matlab编程计算和ADAMS仿真计算，验证了上述位置求解公式的正确性，为求解各树枝构件的配重参数奠定了基础。

3 摆动力完全平衡求解

3.1 有限位置法的基本原理及求解步骤

对于基本回路数为v、自由度为f的平面机构，为实现摆动力完全平衡，需对该机构中(v+f)个树枝构件添加配重；机构摆动力完全平衡时，机构在任意位置上总质量矩为同一常量，故任取机构(v+f+1)个位置上总质量矩，便可建立(v+f)个线性方程组，则机构中(v+f)个配重参数便可求解。

通过有限个位置上的质量矩导出的平衡参数，也同样适用于机构运动的其他任意位置。该方法的特点在于，完成机构位置分析后，取有限个(v+f+1)位置的数值结果建立线性方程组，即可求解得摆动力平衡条件。

为便于理解，给出有限位置法的主要求解步骤，如图3所示。

3.2 各构件参数fi、gi

(1)SKC1: A-B-C(P1)的质量矩求解

构件1、2、3质量矩分别为

(1)

(2)

(3)

由式(1)～(3)相加，可得SKC1质量矩为

(4)

式中M1——SKC1总质量

R1x、R1y——SKC1在x、y方向上的质心位置

(2)SKC2:F-E-D的质量矩求解

构件4、5质量矩分别为

(5)

(6)

由式(5)、(6)相加，可得SKC2质量矩为

(7)

其中M2=m4+m5Cs2x=0Cs2y=0

式中M2——SKC2总质量

R2x、R2y——SKC2在x、y方向上的质心位置

(3)SKC3:E-G-P2的质量矩求解

构件6、7质量矩分别为

(8)

(9)

由式(8)、(9)相加，可得SKC3质量矩为

(10)

其中M3=m6+m7Cs3x=0Cs3y=0

fi=2l4cosθ4+mipigi=2l4sinθ4+miqi

式中M3——SKC3总质量

R3x、R3y——SKC3在x、y方向上的质心位置

进一步，由式(4)、(7)、(10)，得到整个机构质量矩为

(11)

其中

Cx=∑CsxCy=∑Csy

式中M——机构总质量

Rx、Ry——机构总质心位置

各个构件的平衡参数fi、gi(单位:kg·mm)为

(12)

(13)

(14)

(15)

(16)

(17)

(18)

由式(15)可知，构件4的f4、g4，除了与本身质量参数有关，同时还会受到构件5、6、7的影响，这也表明，在树系统划分中，树枝构件6和树枝构件7组成的SKC3，被看作是树枝构件4的子树系统，其子树系统质量矩会影响其质量矩。

3.3 配重参数求解

机构动力平衡时，机构在任意位置上总质量矩相等，由式(11)可知，该机构总质量矩是一个关于θi(i=1,2，…,7)的函数，取机构在5个不同运动位置(v+f+1=5)，各构件角位置记为θik(i表示构件编号，k表示机构运动位置编号，k=0,1，2，3，4)，将θik代入式(11)，可得

(19)

式中MRxk、MRyk——第k个运动位置上机构总质量矩x、y方向上的分量

若取机构中(v+f)个合适的构件((v+f)指整个机构中所有树枝构件的数目)，并附加以适当的配重，使机构摆动力完全平衡，即其总质量矩为常量，则由式(19)可知

(20)

将式(19)代入式(20)，可得

(21)

其中 ΔCik=cosθik-cosθi0ΔSik=sinθik-sinθi0

为便于计算机编程和求解，将式(21)改写成矩阵形式

(22)

其中

ΔCⅡ、ΔSⅡ的形式类比于ΔCⅠ、ΔSⅠ，下标Ⅰ表示树枝构件的位置参数，下标Ⅱ表示连枝构件的位置参数。

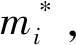
(23)

其中

FⅠ=[f1f2f4f6]T

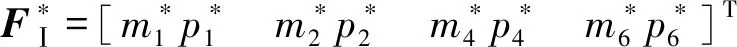
3.4 数值求解

任取机构5个(v+f+1=5)运动位置，即当主动输入角θ1分别为10°、20°、30°、40°、50°时，可求得各构件的角位置变化，并将其代入ΔCⅠ、ΔSⅠ、ΔCⅡ、ΔSⅡ中，可得

将式(12)～(18)及上述求得的ΔCⅠ、ΔSⅠ、ΔCⅡ、ΔSⅡ代入式(23)中，即可求得所有树枝构件的配重参数为

(24)

(25)

(26)

(27)

当主动输入转角θ1分别为30°、60°、90°、120°、150°时，得到各树枝构件的配重参数，和式(24)～(27)计算结果一致，证明了有限位置法的正确性。

4 配重参数敏感度分析及机构平衡分析

敏感度用来衡量机构中某个变量对最终结果的影响程度，敏感度越大表示该变量对最终结果影响较大；一般选择敏感度大的变量进行优化和调整。

4.1 配重参数对总质心轨迹的影响

机构摆动力完全平衡的充要条件是：机构总质心静止不动，即质心轨迹所围成的面积越小，则表示机构质心越稳定。

4.2 配重参数对总惯性力的影响

机构总惯性力为

(28)

4.3 设计变量选取及部分平衡设计

由图8a可知，平衡前后x轴方向的质心轨迹波动极差(最大值与最小值之间的差距)分别为23.4、13 mm，后者比前者优化了44.44%。由图8b可知，平衡前后y轴方向的质心轨迹波动极差为42.04、16.91 mm，后者比前者优化了59.78%。由图8c可知，平衡前机构总质心轨迹所围成面积较大，而平衡后的面积却很小，表明了平衡后机构总质心更加稳定，特别是在y轴方向上波动明显减小。

由图9a可知，平衡前后机构总惯性力在x轴方向的极差分别为0.654、0.177 kg·mm，后者比前者波动减小72.94%。由图9b可知，平衡前后机构总惯性力在y轴方向的最大极差分别为0.37、0.35 kg·mm，后者比前者波动减小5.40%。由图9c可知，平衡前后机构总惯性力的最大极差分别为0.426、0.293 kg·mm，后者比前者波动减小31.22%。

可见，有限位置法的摆动力平衡效果较为有效。

5 结论

(1)采用有限位置法对具有两个末端执行器的零耦度平面高速冲压机构进行了动平衡计算，得到了机构摆动力完全平衡条件，并对其进行了数值求解验证。