考虑疲劳累积损伤的FRP-混凝土界面剥离模拟

郭佳泷,应 杰,章子华*,肖云逸

（1.宁波大学 土木与环境工程学院,浙江 宁波 315211;2.浙江头门港投资开发有限公司,浙江 台州 317015）

外贴FRP 加固是目前常用的结构加固方法之一.疲劳荷载作用下,FRP-混凝土界面黏结性能会逐步劣化,并导致整体结构承载能力和可靠度下降.为准确评估疲劳荷载效应对界面黏结性能的影响,防止由此造成界面剥离和结构失效,有必要对考虑疲劳累积损伤界面黏结性能进行深入研究.

针对FRP 与混凝土的疲劳黏结性能,国内外学者已开展了大量的试验研究.马涛等[1]通过单剪试验发现CFRP 黏贴长度、厚度和混凝土强度等对CFRP 与混凝土的黏结强度有较大影响,循环荷载的上限比例越高,上述参数对界面疲劳黏结性能影响越大.李树霖等[2]通过双剪试验发现界面疲劳损伤程度与胶层厚度存在相关性,且胶层厚度越大,胶层对抑制黏结界面损伤和刚性退化效果越好.Bizindavyi 等[3]通过单剪试验对GFRP-混凝土界面的疲劳性能进行了研究,考虑黏结长度、黏结宽度对疲劳荷载下界面黏结应力的影响,得到界面在疲劳荷载下的S—N曲线.Diab 等[4]对FRP-混凝土界面的疲劳性能进行了试验研究,基于Paris公式得到了疲劳荷载下界面的黏结滑移模型和界面开裂扩展模型.曹文海等[5]通过双剪试验发现在疲劳荷载条件相同的情况下,采用柔软树脂试件的黏结界面疲劳性能更好;通过液体橡胶对普通树脂进行增韧改性,能够有效改善界面的疲劳受力性能,提高其疲劳寿命[6].需要指出的是,FRP-混凝土界面疲劳性能的部分研究结果存在不一致甚至矛盾.例如,Mazumdar 等[7]指出,疲劳强度与极限承载力都与黏结长度成正比,而Jen 等[8]发现在胶层厚度为1 mm 或1.5 mm 时的疲劳强度与黏结长度成反比.Tamura 等[9]发现FRP-混凝土界面的极限承载力与胶层厚度成正比,疲劳寿命与胶层厚度成反比,而Xu 等[10]则发现随胶层厚度增加,疲劳破坏裂缝出现迟缓的现象.此外,由于FRP-混凝土界面疲劳性能的测试难度和数据离散性大,导致不同研究得到的FRP-混凝土界面疲劳退化规律也不一致.为探明疲劳荷载作用下FRP-混凝土界面疲劳损伤演化机理,需对现有界面疲劳试验数据进行筛选,并通过理论方法和有限元模拟对考虑疲劳累积损伤的界面剥离机理进行分析.

本文在现有文献中收集归纳了14 组，共计82个FRP-混凝土界面纯剪切疲劳试件[3,5,11-14].其中,Bizindavyi 等[3]和Min 等[14]采用单面剪切试件,其余均采用双面剪切试件.一般认为,疲劳荷载下FRP-混凝土界面疲劳寿命与荷载幅值服从指数函数关系[15],故采用下式对各组试验数据进行拟合:

式中:ΔP为荷载幅值;N为FRP-混凝土界面疲劳寿命;a、b为拟合参数.

图1 各组剪切疲劳试件的ΔP—N 曲线

从图1 的拟合结果可见,韩强[12]组的试验数据相对充分,且拟合相关性较好,其主要原因是该组试验采用了双面剪切试件,能够有效避免单面剪切试件中由于对中误差导致界面并非为纯剪切状态的现象,而且从试件、锚固等方面对双面剪切试件进行了改进,使疲劳荷载的加载更加稳定,疲劳试验数据的离散性更小.故后文采用该试验获得的FC 组数据进行理论分析与数值模拟.

1 FRP-混凝土界面黏结疲劳退化模型

以静载作用下界面黏结滑移曲线为基础,将静载作用下界面的黏结滑移曲线作为某次疲劳荷载循环下的黏结滑移曲线依据,建立不同疲劳荷载循环次数下的黏结滑移关系,Loo 等[16]由此提出了疲劳荷载下界面黏结疲劳退化双线性模型.如图2 所示,其中,τave,max为界面疲劳破坏过程中平均黏结剪应力的最大值,Nf为破坏时的循环次数,smax为峰值应力对应的滑移量.双线性模型的控制参数为界面初始刚度、界面峰值剪应力、界面残余滑移量,确定这3 个参数与荷载循环次数N的关系即可确定疲劳荷载下界面的黏结滑移关系,并可进一步得到不同荷载循环次数下的界面断裂能,为确定不同循环次数下界面的剩余承载能力提供理论基础.

图2 FRP-混凝土界面黏结疲劳退化双线性模型

2 界面黏结疲劳退化双线性模型关键参数分析

2.1 界面残余滑移量的疲劳退化规律

疲劳荷载下界面的残余滑移量难以直接获得,但可通过沿黏贴长度方向在FRP 上的相邻黏贴应数值得到局部滑移量s的大小,进而得到不同循环次数下的界面残余滑移量Δs.将界面i处的滑移量定义为FRP 的滑移量与混凝土之间滑移量的差值,即:

式中:wc为混凝土之间的相对滑移量;ls为应变片的间距;εi为i处FRP 应变;ε0=P/(2bftfEf),P为荷载值;tf、bf和Ef分别为FRP 的计算厚度、黏结宽度和弹性模量.

联立式(2)、(3),并结合疲劳试验数据[12],可得不同循环加载次数下的残余滑移量(表1).

2.2 界面峰值剪应力的疲劳退化规律

根据FRP 表面应变,通过差分法求得FRP 表面平均黏结剪应力,即:

式中:τ和σ分别为FRP 表面剪应力和正应力.

在此基础上,可获得不同循环加载次数下的峰值剪应力(表1).

2.3 界面初始刚度的疲劳退化规律

在界面剪切刚度双线性疲劳模型中,第n次循环加载后界面的初始黏结刚度为[12]:

式中,Bn、τn、sn和Δsn分别为第n次循环加载后界面的初始黏结刚度、黏结强度、相对滑移量和残余滑移量.

将不同循环加载次数下的黏结滑移数据代入式(5),则可得到不同循环加载次数下的界面初始刚度(表1).

2.4 疲劳荷载下界面黏结滑移关系

基于FRP-混凝土界面的面内剪切疲劳试验数据[12]和界面剪切刚度双线性疲劳模型,可得到不同荷载循环下的界面黏结滑移关系:

式中:sn,0为第n次荷载循环时峰值剪应力对应的界面相对滑移量;su为界面极限滑移量;τn,max为第n次荷载循环时界面峰值剪应力.

2.5 不同循环加载次数下的界面断裂能

界面断裂能Gf表示界面发生断裂破坏时单位面积消耗的能量,而界面断裂能的大小可作为评判界面黏结性能的指标.静载下的FRP-混凝土界面断裂能可以通过对静载下FRP-混凝土界面黏结滑移曲线进行积分,以界面黏结滑移曲线与坐标轴包围的面积表示界面断裂能的大小.而对于疲劳荷载下FRP-混凝土界面断裂能的演变,已有研究中缺少合适的界面断裂能计算公式,因此有必要对不同荷载循环次数下的FRP-混凝土界面断裂能进行研究.

由于双线性模型可直接计算出曲线包围面积,故以界面黏结疲劳退化双线性模型[17]为基础,假定不同荷载循环次数下黏结滑移曲线的下降段不变,则在同组试件中极限滑移值su也不变.在得到残余滑移量s0、峰值剪应力τmax、极限滑移量su这3 个关键参数后,即可建立界面断裂能与荷载循环次数的关系:

式中:Gn,f为第n次荷载循环时的界面断裂能.

根据式(7)即可得到在不同荷载循环次数下的界面断裂能(表1).

3 FRP-混凝土界面疲劳失效有限元模拟

3.1 内聚力接触

内聚力模型(Cohesive Zone Model,CZM)是一种有效的断裂力学方法,其通过零厚度内聚力单元的黏结滑移关系来表征断裂过程区的能量耗散,能有效避免裂尖应力奇异和网格重构所引起的数值求解困难,是复合材料界面断裂的理想模拟手段[16].本文采用较适用于胶层的损伤失效模拟的双线型内聚力模型来模拟界面的剥离过程[18-20].其法向和切向的本构关系可表示为:

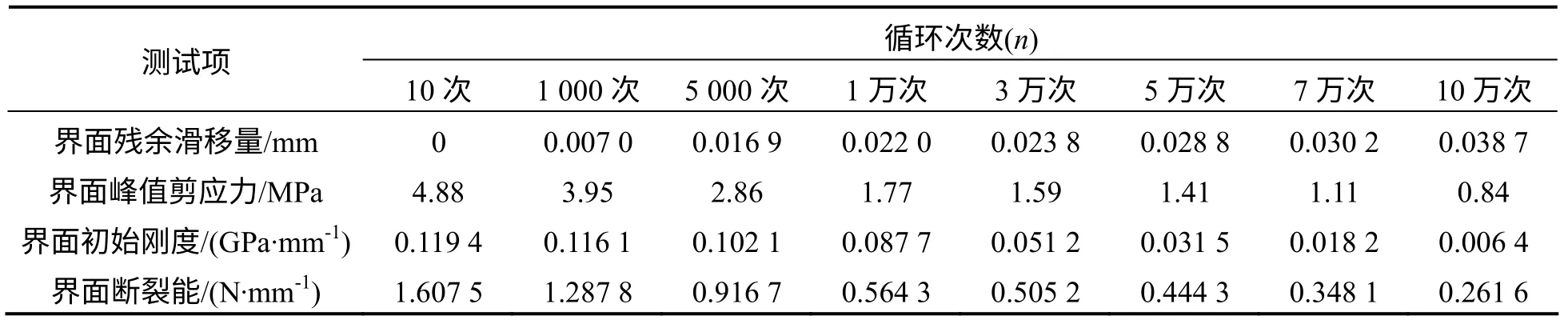
表1 试件在不同循环加载次数下界面的残余滑移量、峰值剪应力、初始刚度、断裂能

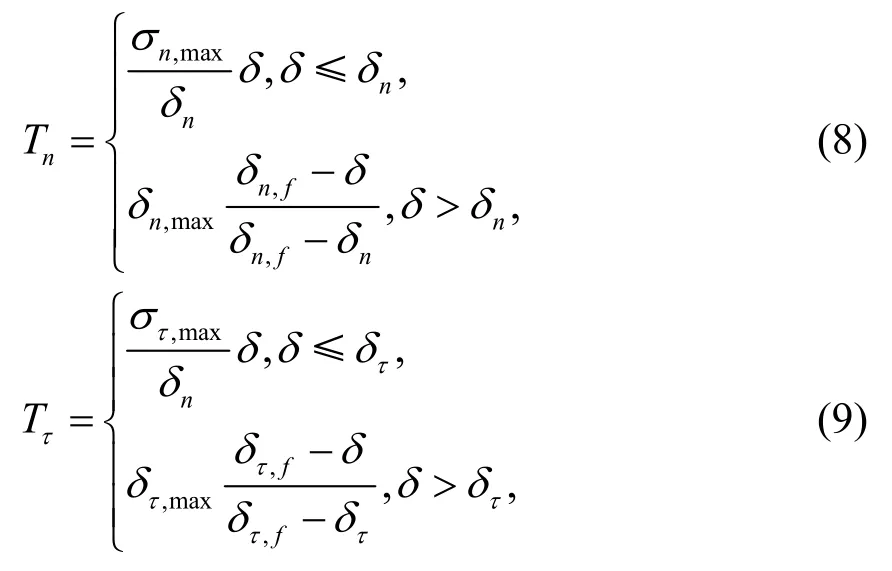
式中:Tn和Tτ分别为法向和切向应力值;σn,max和στ,max分别为法向及切向应力峰值;δn和δτ为应力峰值时对应的相对位移;δn,f和δτ,f表示应力为零时对应的相对位移.

以最大名义应力准则作为判定界面开始发生损伤的依据,即:

式中:tn,0为与界面垂直的纯法变形时的最大名义应力;ts,0和tt,0分别为与界面相切的两个方向纯切向变形时的最大名义应力.

材料界面产生初始损伤后,损伤扩展由界面断裂能释放率来控制.采用幂法准则来描述单元损伤的扩展,即:

式中:Gn,c、Gs,c和Gt,c分别为法向及两个切向的临界释放率;Gn、Gs和Gt分别为法向及两个切向的能量释放率;η和α为试验拟合参数.对于FRP 材料而言,通常η和α均取1.

3.2 有限元模型

根据对称性,取双剪试件[12](图3)的二分之一进行建模,其有限元模型如图4 所示.混凝土试块尺寸为250 mm×100 mm×50 mm,FRP 黏贴范围为250 mm×50 mm,在FRP 加载端施加静载P.混凝土试块前后端面均采用固端约束.混凝土采用C3D8R 单元,FRP 采用S4R 壳单元.

图3 双面剪切试验示意图

图4 双面剪切试件有限元模型

3.3 材料参数

鉴于FRP-混凝土剥离失效仅发生在黏结层中,故可将混凝土视为线弹性体,而可不考虑混凝土塑性损伤,以减少计算量.根据《混凝土结构设计规范》[21],混凝土弹性模量、泊松比和密度分别取30.2 GPa、0.2、2 300 kg∙m-3.作为一种正交各向异性材料,CFRP 的材料参数取值参考文献[18],分别为E1=187 GPa,E2=E3=8.27 GPa,G12=G13=4.14 GPa,G23=3.45 GPa,μ12=μ13=0.26 和μ23=0.34.

疲劳累积损伤体现在界面接触的初始刚度K与界面断裂能Gn,f的折减,其中初始刚度K根据2.3节方法进行折减,界面断裂能则根据2.5 节方法进行折减,界面断裂能Gn,f取值见表1,其余界面层参数列于表2.Knn、Kss、Ktt、tn、ts、tt具体参数参考文献[19-20].

表2 界面层材料参数

4 结果与讨论

4.1 FRP 表面应力与混凝土表层黏结剪应力

图5 为试件在10 次、3 万次、10 万次疲劳荷载后,施加静载剥离破坏的FRP 表面应力分布情况.由图可见,在同一时刻下,不同疲劳荷载次数下FRP表面应力的大小不同,说明疲劳荷载造成了显著的界面损伤并随着循环加载次数的增加而累积.由于整个界面的剪切刚度和断裂能采用了统一的折减系数,故不同循环加载次数下的应力分布是类似的.从应力传递过程看,试件在加载初期,应力峰值位于加载端,随着荷载的增加,FRP 应力峰值由加载端向自由端发展.在FRP-混凝土界面剥离过程中(图5(b)),界面剥离边缘存在显著的应力集中现象.在界面剥离末期,FRP 表面应力发生了明显的重分布,峰值应力呈U 型分布,并开始卸载.从开始加载到界面剥离,界面自由端有一段区域始终无应力,这说明FRP-混凝土界面存在一个有效黏结长度.

图5 FRP 表面Von Mises 等效应力云图

图6 为试件在10 次、3 万次、10 万次疲劳荷载后,施加静载剥离破坏的黏贴区混凝土表层黏结剪应力分布云图.由图可见,在加载初期,加载端黏结剪应力迅速增大,并逐渐向自由端传递,靠近自由端的剪应力几乎为零.在界面剥离过程中,随着荷载的增大,峰值剪应力逐渐向自由端传递.

图6 混凝土表层黏结剪应力云图

4.2 黏结滑移曲线

在有限元分析中无法直接提取界面的黏结滑移曲线.因此本文采用Dai 模型[22]对试件不同荷载循环下的应变模拟值进行拟合,即:

对式(12)关于x积分,可得界面滑移分布:

对式(12)求导后代入式(4),并联合式(13),即可得到剪切试件界面黏结滑移关系式:

式中:a、b均为拟合参数;x为距加载端的距离;x0为峰值剪应力距加载端的距离；tf、Ef分别为FRP的计算厚度和弹性模量.

将有限元分析得到的FRP 表面应变代入Dai模型,即可得到试件在不同荷载循环次数下的黏结滑移曲线(图7).由图可见,模拟所得界面黏结滑移曲线由线性上升段、曲线上升段和曲线下降段三部分组成,与试验所得界面黏结滑移曲线特征一致[6].随着荷载循环次数的增加,曲线峰值剪应力逐步减小,也与试验吻合[12].黏结滑移曲线与坐标轴包围的面积随着荷载循环次数的增加而减少,说明随着荷载循环次数的增加,界面剩余黏结承载能力逐渐减弱.在荷载循环次数小于1 万次时,黏结承载能力下降的速度较快,而在1 万次至10万次之间时,黏结承载能力下的速度逐渐变缓.值得注意的是,由于在理论模型中假定黏结滑移曲线下降段保持不变,以黏结界面初始刚度和峰值剪应力的退化来体现疲劳损伤,因此,随着荷载循环次数的增加,峰值剪应力逐渐减小,而极限滑移量保持不变.而从有限元结果看,不同荷载循环次数下有限元模拟获得的峰值剪应力与理论模型接近,界面极限滑移量略有不同.因为界面断裂能的几何意义为该曲线与横坐标所包围的面积,为了保证模拟达到与理论模型一样的界面断裂能,模拟曲线下降段变得更加平缓,导致模拟的极限滑移量比理论模型大.随着荷载循环次数的增加,有限元模型和理论模型中的黏结界面初始刚度均逐渐减小.由此可见,本文方法能有效获得考虑疲劳累积损伤的界面剥离特征.

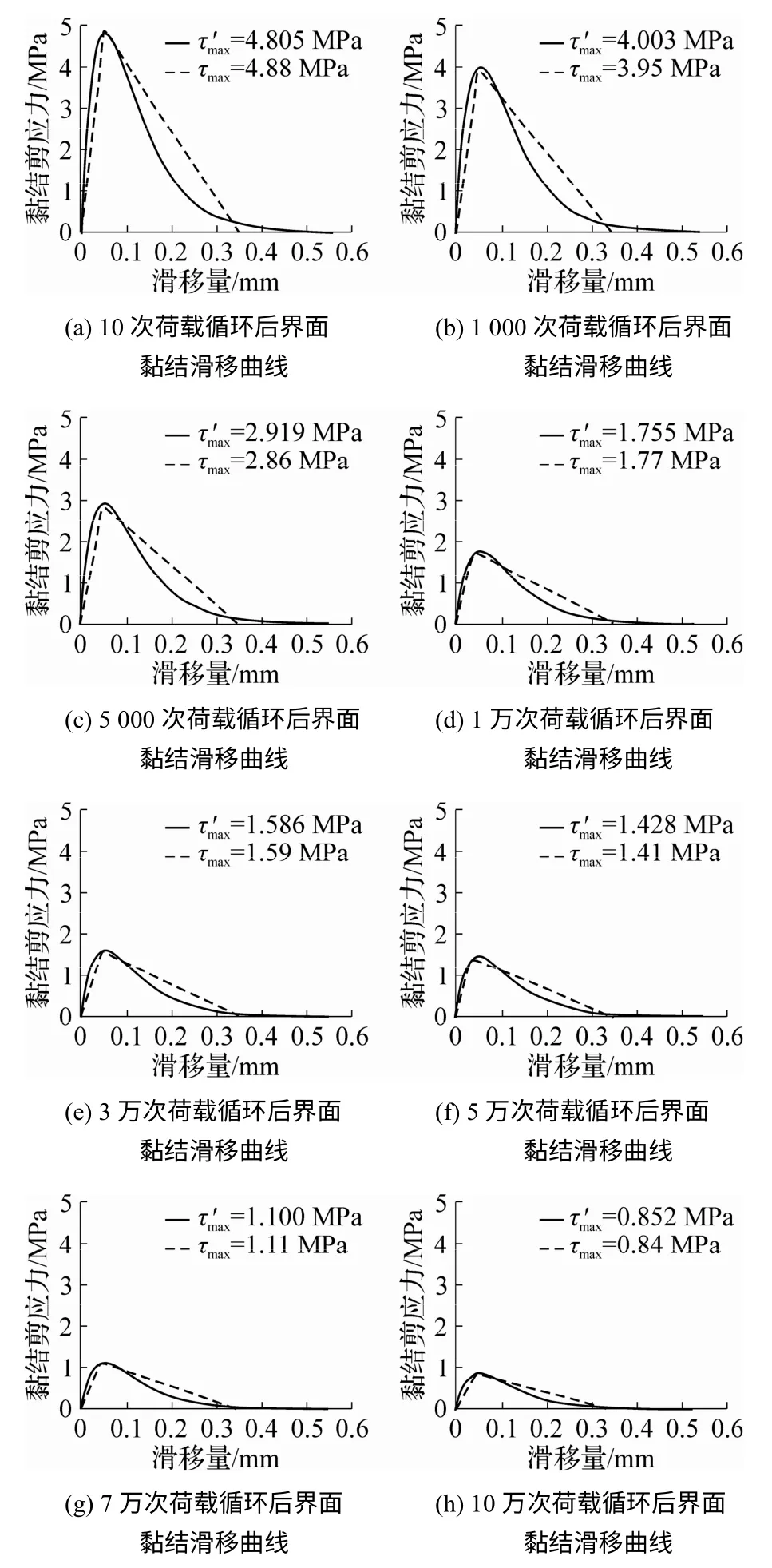
图7 不同循环加载次数下界面黏结滑移曲线对比

图8 不同循环加载次数下峰值剪应力模拟预测模型

将图7 中的模拟结果通过峰值剪应力与荷载循环次数退化关系表达式τmax=a+b˙Nc进行拟合,得到不同循环加载次数与峰值剪应力的关系,具体曲线如图8 所示.

5 结论

本文在已有疲劳试验的基础上,从理论模型、数值模拟两方面入手,对疲劳荷载下FRP-混凝土界面黏结性能展开了研究,得到了不同荷载循环次数下的界面黏结滑移曲线,对比理论模型与有限元模拟结果,得到了以下主要结论:

(1)基于界面黏结疲劳退化双线性模型,对已有的疲劳试验数据进行分析,获得了界面残余滑移量、界面峰值剪应力和界面初始刚度的疲劳退化规律.疲劳荷载作用使黏结界面的微裂纹或微孔隙形成并扩张,并随界面损伤的累积,微孔隙或微裂纹相互贯通,导致界面黏结力逐步丧失,黏结应力相应减小,峰值剪应力也会逐渐下降.随荷载循环次数增加,界面滑移后的不可恢复段增大,界面残余滑移量增加,在较低应力作用下仍有较大黏结滑移,导致界面初始刚度也减小.并在此基础上,建立了不同循环加载次数下的界面黏结滑移关系.

(2)双线性模型虽不能准确描述界面剥离的非线性过程,但可以直接简便地获得不同循环加载次数下的界面断裂能.基于双线性模型的有限元模拟结果符合实际的界面剥离过程,所得峰值剪应力、界面断裂能、界面剪切刚度等与理论模型接近,但极限滑移量与理论模型有所区别,其黏结滑移曲线特征与典型试验曲线一致.因此,本文所提方法是一种有效的考虑疲劳累积损伤的FRP-混凝土界面剥离模拟手段.

(3)从有限元模拟结果看,疲劳荷载作用会显著降低界面承载力,荷载循环次数在1 万次内时影响较为明显,但界面破坏特征并未发生显著变化.