基于流固耦合的涡轮增压器涡轮机温度场分析

石永康,陈振雷,王 勇,刘攀勇

（宁波大学 海运学院,浙江 宁波 315832）

涡轮增压器主要组成部件有涡轮机、压气机和中间壳体[1],与发动机进排气管相连[2].这些部件通常由不同材料组成,压气机吸取新鲜空气,涡轮机抽取废气[3].废气的温度很高,涡轮壳表面形状复杂,且温度分布梯度较大,热应力是导致涡轮损坏的主要原因.已有学者对涡轮增压器各零部件的疲劳与强度做了很多研究.如Kim等[4]利用有限体积法(Finite Volume Method)和工程设计仿真软件(ANSYS)对环形内冷通道的燃气轮机叶片进行传热和应力分析,但只对叶片的传热系数进行了研究.Li 等[5]采用有限元和试验相结合的方法得出涡轮增压器叶片固体模态和频率,但并未考虑温度场对叶片的影响.胡友安等[6]利用有限元分析了涡轮壳温度场和热应力,但未考虑全域流固耦合的传热过程.目前,采用全域流固耦合方法对涡轮增压器涡轮壳表面及涡轮机内部零部件的温度场研究尚未见报道.

本文采用全域流固耦合方法对涡轮增压器涡轮机各零部件温度场进行了分析,包括涡轮壳、蜗壳、盖板等主要零部件,建立了高温状态下全域流固耦合数值模型,为准确评估涡轮机强度提供了与测试结果相一致的全域温度场.

1 理论分析

1.1 控制方程

采用有限元方法对涡轮机内部的流体进行仿真分析,高温废气流动和传热过程需要遵循质量守恒方程、能量守恒方程和动量守恒方程[7].

连续方程:

式中:ρ为流体密度;t为时间;ui为流动速度.

动量方程:

式中:p为流体压力;μ为流体动力黏度;为雷诺应力.

能量方程:

1.2 湍流模型

一般认为非稳态连续方程与Navier-Stokes 方程对复杂的湍流运动仍然适用,但还无法利用微分方程精确求解湍流流场.工程上广泛采用壁面函数可调的k-ε湍流模型[8],其中k是湍流动能,ε是单位质量湍流动能的耗散率[9].简化的标准k-ε模型为[10]:

式中:μt为湍流黏性系数;Sij为应变率(速度对坐标导数);σk=1.00,σε=1.30,C1ε=1.44,C2ε=1.92,分别为普遍使用的常数值.

2 传统模型

有资料表明[11],国际顶级涡轮增压器涡轮机分析模型采用参照数据库在涡轮机内外壁面按区域赋予温度和热交换系数,且不考虑涡轮机内部高温气流及其与固体域的热交换,计算分析涡轮机温度场,即对所有的涡轮机壁面施加固定的壁面温度和热交换系数.该传统模型的优点是计算简单、快速,但前处理过程复杂,且计算结果受假设条件影响,精度低.

表1 为本文对应传统模型所假设的某涡轮机入口气流温度为950 ℃的边界条件.

表1 传统模型边界条件假设

续表

图1为采用Hypermesh软件建立的涡轮机传统模型.图2 为采用传统模型分析方法得到的涡轮机整机温度场分布云图.下面将上述结果与本文建立的全域流固耦合模型进行对比.

图1 涡轮机传统模型

图2 传统模型的涡轮机整机温度场分布(单位℃)

3 全域流固耦合模型

3.1 网格模型

与传统模型不同,全域流固耦合模型将整个模型分为3 个部分:内部流体域、固体域和外部流体域.内部和外部流体域与涡轮机在接触面以热对流和热传导方式进行热交换,无需假设壁面温度与热交换系数;在外部流体域设置环境温度、标准大气压;在涡轮机进出口边界上有测试结果可以给出准确的进/出口温度与压力边界条件,模型将自动完成热交换迭代计算.在流体域与涡轮机接触的表面,同时发生流、固、热3 场能量交换与传递,这是一个复杂的能量变化过程[12-13].在流固传热边界上的能量守恒定律[14]可表示为:

因此在离散过程中,对流体和固体接触区域进行加密,以期获得满意的计算精度.整个模型的网格信息如图3～5 及表2 所示.

图3 空气域网格

图4 固体域网格

图5 流体域网格

3.2 材料属性和边界条件

将高温废气在涡轮机内的流动视为三维不可压缩黏性流动,高温废气与涡轮机的传热过程视为稳态传热,废气在涡轮流道内的流动属于湍流流动,在Fluent 软件中选用不可压缩气体标准的k-ε湍流模型.高温废气是燃烧后产生的废气,主要成分为:N2、O2、H2O、CO2、CO 等[15].根据工程热力学气体混合参数的计算方法可得出高温废气属性:密度0.705 9 kg·m-3,导热系数0.050 19 W·(m·K)-1,动力黏度 3.18×105(N·s)·m-2,比热1120.50 J·(kg·K)-1,湍流普朗特系数0.90.

全域流固耦合模型在传统模型的基础上增添了内部流体域和外部流体域,建立了完整的流固耦合计算体.对于传热模型计算,涡轮进口给定压力进口,出口选择压力出口,边界选用压力边界,具体参数见表3.

表3 边界条件设定(压力表测定)

4 计算结果与分析

通过Fluent 软件进行数值模拟,涡轮机内部流体视为黏性不可压缩湍流流动,采用coupled 算法[16],动力学模型采用标准的k-ε湍流模型[17],收敛精度10-6,计算达到收敛后得到涡轮机整机温度场分布.

4.1 涡轮机整机温度场分析

图6 为全域流固耦合涡轮机整机模型的温度分布.

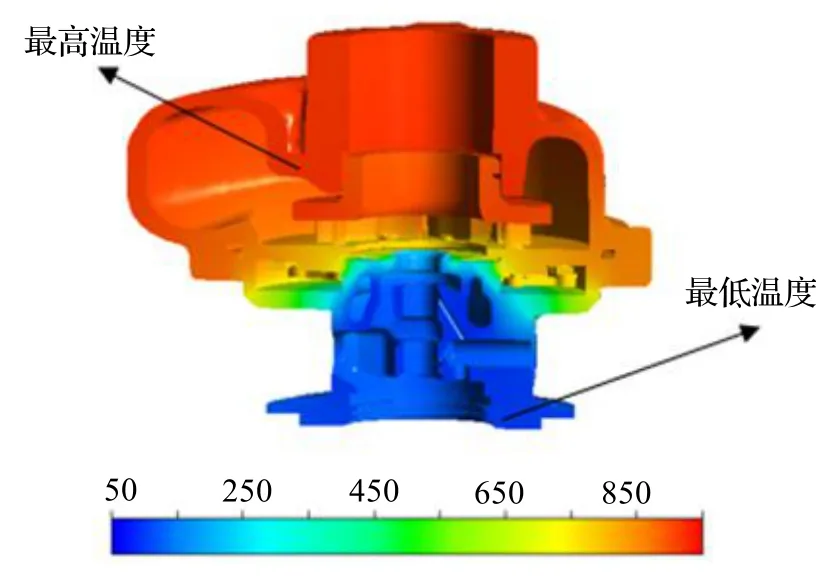
图6 全域流固耦合涡轮机整机模型的温度分布(单位℃)

从图6 可知,涡轮壳整体温度分布广,温度梯度大,在50～950 ℃之间.涡轮壳壳体表面较高温度区间出现在涡轮壳的进口处到靠近废气出口一侧,最高温度可达936.3 ℃;而较低温度区间则出现在底座区域.

涡轮壳的热量主要来源于高温废气,高温废气直接与涡轮壳接触,因此沿着高温废气的流动方向能量逐渐减少,温度逐渐降低.涡轮壳壳体上温度最高点出现在废气出口侧附近,其原因是此处与外界直接接触面积和散热量小.

4.2 蜗壳温度场比较分析

通过图7(a)传统模型蜗壳温度场分布与图7(b)全域流固耦合模型蜗壳温度场分布的比较可知,后者蜗壳温度分布符合实际情况,而前者结果不甚合理.

图7 蜗壳温度场分布(单位℃)

由于950 ℃高温废气从蜗壳入口流入蜗壳流道,高温废气与蜗壳接触面进行换热,使高温废气的能量随着蜗壳流道的深入逐渐减少,因此蜗壳温度分布应该是废气入口处最高.

表4 为2 种模型蜗壳流道仿真点温度的比较.从表4 可看出,全域流固耦合模型随着蜗壳流道的深入温度逐渐降低,符合实际情况.

表4 2 种模型蜗壳流道仿真点的温度比较 ℃

4.3 典型零部件温度场分析

通过传统模型盖板温度场分布(图8(a))与全域流固耦合模型盖板温度场分布(图8(b))的比较可以看到,2 种模型的盖板整体温度分布在890～930 ℃之间,盖板整体温度较高;传统模型盖板温度分布不规律,全域流固耦合模型盖板在螺栓连接处温度呈梯度下降,且温度分布有规律.据此认为,全域流固耦合模型盖板温度场分布比传统模型盖板温度场分布更为合理、可靠.

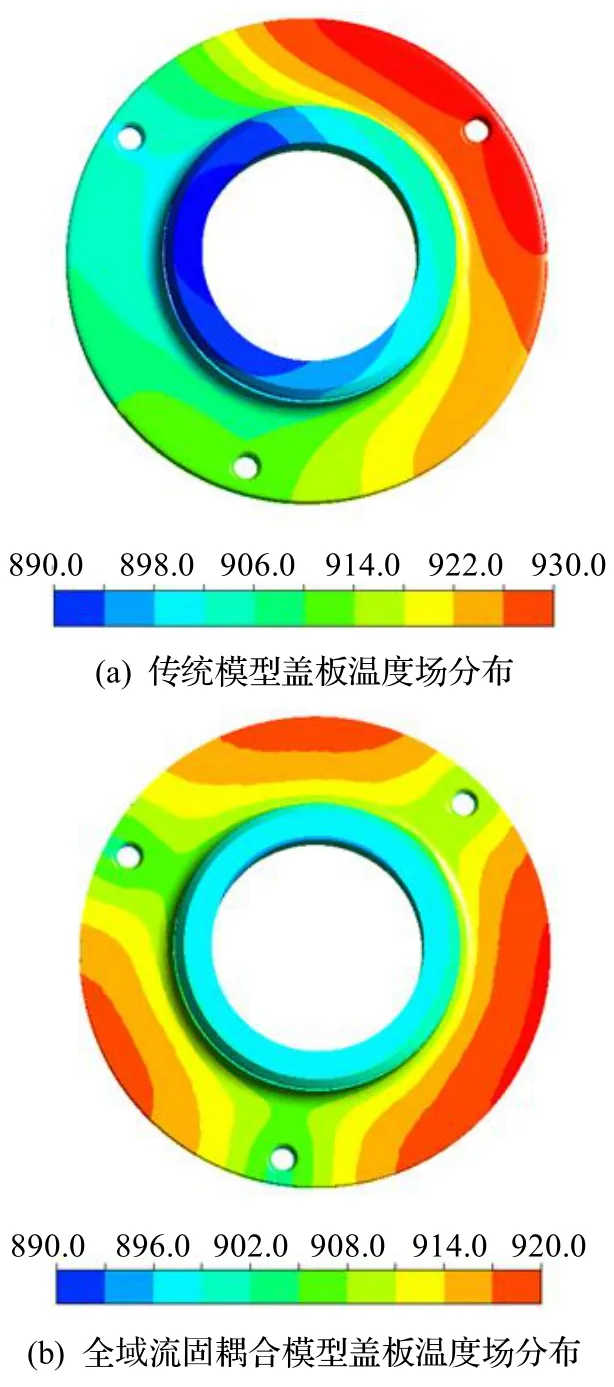
图8 盖板温度场分布(单位℃)

5 实验验证

在涡轮机外壳上选取10 个温度监测点(图9),待发动机正常运转30 min 进入稳态后,对上述监测点的温度进行测量,并与数值模拟得到的计算值进行比较,结果见表5.

图9 涡轮壳外壳监测点

表5 监测点数值模拟值与实验值对比

传统模型数值模拟结果与各监测点的实验测量值误差最高达15.27%,而全域流固耦合模型数值模拟结果与测试值间的误差均在5%以内.可见利用全域流固耦合传热数值模拟的方法对涡轮增压器涡轮的温度场分析准确、可靠.

6 结论

(1)针对涡轮内部零件受热不均匀和热变形不均导致涡轮壳开裂等问题,建立了涡轮增压器涡轮的全域流固耦合数值模拟仿真计算流程,计算分析了涡轮的温度场,为准确评估与优化涡轮壳开裂提供了参考.

(2)涡轮机整体温度分布范围在50～950 ℃之间.涡轮机内部零部件较高温度区域出现在盖板和蜗壳上,这两部件的大部分区域温度基本保持在750 ℃以上.

(3)与实验测试结果相比,全域流固耦合模型的相对误差在5%以内,而传统模型的最大误差为15.27%.可见全域流固耦合模型比传统模型涡轮机温度场的计算结果更为合理、准确.