二维任意凸四边形网格的MoF界面重构解析算法
2021-05-19王成孔泽宇李涛贾祖朋
王成, 孔泽宇, 李涛, 贾祖朋
(1.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081;2.北京应用物理与计算数学研究所,北京 100088)
流体矩(moment of fluid,MoF)方法是一种分段线性网格重构方法,主要用于多物质流体数值模拟中进行界面重构,是目前VOF方法群中最为先进的一种. 该方法可以在单元尺度上进行界面重构,只依赖于单元内部数据,精度有着显著的优势[1]. 在前人的成果中,MoF界面重构方法应用在很多情况中. 例如,在自适应网格问题中利用MoF方法的形心数据判断高曲率区域进行界面细分[2];在任意拉格朗日-欧拉模型中采用MoF方法的形心数据,对非结构网格上的二维可压缩流体进行界面重构[3],以及直接采用MoF方法进行多物质条件下的ALE界面重构[4]. 另外的一些针对方法的研究中,在轴对称坐标系下进行了MoF方法界面重构[5],进一步在柱坐标的ALE方法的MoF方法的界面重构实现[6];通过使用对称重构方法,使多物质MoF过程中实现两材料的矩量对称计算,同时提高计算精度和计算效率[7];使用丝状网格界面捕捉方法,在二维薄网格难以进行常规界面重建处理的情况下实现了MoF方法,进而实现了网格尖端处的界面重构精度提升[8]. 针对MoF的界面求解精度和求解效率,一些研究中提出了求解一阶偏导数以提高迭代效率和鲁棒性的方法[9],证明对目标函数求解解析一阶偏导数对混合单元问题界面重构问题的解决效率有着较大的提升. Antoine Lemoine等[10]探究了正交网格的界面解析重构,在笛卡尔坐标下甚至所有矩形网格中实现了解析解的界面重构工作,结合王成等[11]的重映改进方法,可以大幅提升界面重构的计算精度和计算效率并应用在MMALE方法中. 本文对这一思路进行了更进一步的尝试,在更为广泛的凸四边形网格中实现解析解的界面重构.
1 传统MoF方法中的界面重构
1.1 MoF方法简介
在传统的MoF方法处理多物质网格界面重构问题时,一般采用的是数值计算迭代寻找曲面的最优近似的方法. MoF方法重构界面主要依靠多边形网格Ω中的各物质子集ω的零阶矩M0(ω)和一阶矩M1(ω)来计算[1],
(1)
在一般情况下,前两阶矩的等价量有着实际的物理意义,即体积分数μ(ω)和形心xc(ω):
(2)
因此,MoF方法一般使用物质的体积分数和形心来进行界面重构.
MoF界面重构的核心问题在于找到实际的物质子集ω*的一个最优多边形子网格近似ω*,这个近似子网格的边界Γ*是实际界面Γ的一个最优近似,如图1所示.
由于MoF方法是体积守恒的,因此更进一步地说,确定这个近似子网格ω*是一个求最小值的问题,即找到一个多边形近似子网格ω*,使得实际物质子集ω的形心xc(ω)和这个子网格的形心xc(ω*)距离最小.
(3)
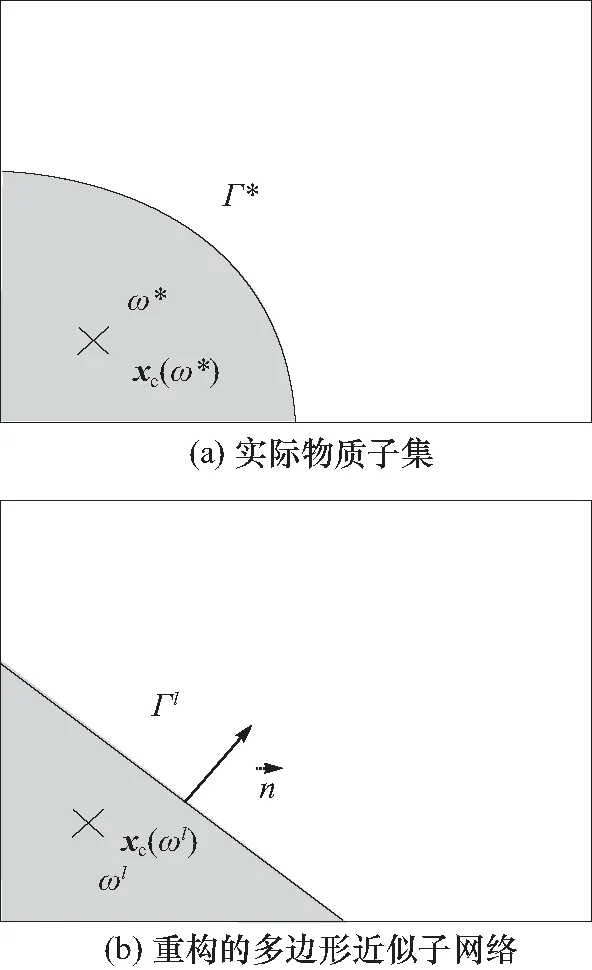
图1 实际物质子集和重构的多边形近似子网格
1.2 传统MoF界面重构方法
在传统的MoF方法中,求解最小值问题通过迭代图1(b)显示的界面法向量角度来实现,在保证体积分数μ(ω)不变的条件下,每选定一个法向量n,就可以对应确定一个线性子网格界面Γ*,进而求解出多边形子网格的形心xc(ω*),进一步找出一个法向量n0使得这个情况下的多边形形心xc(ω*)与实际形心xc(ω)之间的距离最近. 求解过程中法向量n迭代旋转角度决定了迭代求解的精度. 为了简化这一过程,贾祖朋等[1]采用了Brent迭代、限定旋转范围等各种方法进行迭代,在此不再一一说明.
1.3 解析解求解凸四边形MoF界面重构方法
对任意的一个凸四边形网格,进行线性界面重构后形成的两个子网格形状可能性是有限的,针对不同形状的每一个子网格都可以求解出这个子网格情况下的一个物质形心(x*,y*),(x*,y*)随着界面的变动而运动,因为界面的运动是连续的,所以(x*,y*)的运动也是连续的,即所有的子网格形心(x*,y*)可以组成一条曲线F(x*,y*).
当物质的实际子网格ω形心(x,y)已知时,MoF方法的求最小值问题简化为计算曲线F(x*,y*)上距离形心(x,y)最近的一个点. 当曲线复杂度不高时,可以直接计算出该点.
2 对任意凸四边形网格的切分
2.1 对任意四边形网格的旋转简化
x′y′坐标系内任意的一个四边形A′B′C′D′,首先将其平移至xy坐标系中的ABCD位置,令点A与xy坐标系的原点重合;然后旋转坐标系,使得向量AB在xy坐标系中为(1,0). 旋转方程为:
(4)
坐标变换后存在4个互相独立的未知变量xC、yC、xD、yD,其中点D在AD边上,可以用AD边斜率倒数k1和点D的y坐标yD来表示点D位置:
xD=k1yD
(5)
同样地可以使用BC边斜率倒数k2和点C的y坐标yC来表示点C的位置
xC=k2yC+1
(6)
从而可以利用4个独立变量率k1、yC、k2、yD确定四边形的位置.
2.2 凸四边形网格的限制条件

(7)
而若k1≤k2,则四边形网格必然存在. 综合两种情况,得到四边形网格的限制条件为
(8)

2.3 凸四边形网格拆分情况
采用一个线性界面拆分凸四边形网格,存在如图2所示的以下4种情况:

图2 四边形网格一次拆分可能性
① 2个交点位于相邻的2条边上,线性界面将四边形网格拆分成1个三角形和1个五边形;
② 2个交点位于一组对边上,线性界面将四边形拆分为2个四边形;
③ 1个交点与四边形的1个节点重合,另一个交点在这个节点的2条对边之一上,线性界面将四边形拆分成一个三角形和一个四边形;
④ 2个交点分别是对角的2个四边形节点,线性界面将四边形网格拆分成2个三角形.
其中情况③和情况④可以视作情况①和情况②的一种特殊情况. 因此,在进行解析解计算时,只需要考虑三角形子网格和四边形子网格的情况,对五边形子网格的情况可以通过对侧的三角形的形心x(1)与体积V(1)和整个网格的形心xcell与体积Vcell来推导出五边形子网格的形心x(2),
(9)
3 任意凸四边形的解析解求法
在本节中,首先考虑的是交点位于AD边和AB边时拆分出三角形的情况,其他拆分出三角形的情况可以通过轴变换直接转变到这种情况;其次考虑交点位于AD边和BC边时的拆分出2个四边形的情况,同样的,其他拆分出四边形的情况也可以通过轴变换的方法来转变成这种情况.
3.1 拆分出三角形的情况

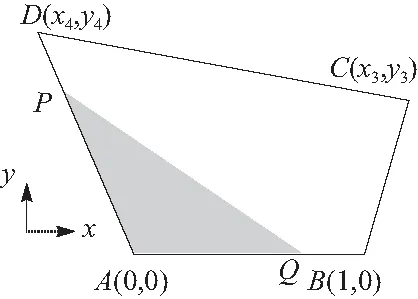
图3 四边形网格拆分出三角形网格的示意图
因此,对情况①中的三角形,其形心和体积可以给定为
(10)
可以推出x*和y*之间的关系为
(11)
根据二次曲线的性质[12],三角形形心(x*,y*)轨迹曲线为一条双曲线. 对于给定形心(Px,Py),在这条双曲线上距离给定形心最近的一点(x*,y*)与给定形心(Px,Py)的连线一定垂直于双曲线在点(x*,y*)处的切线,求解得:
(12)
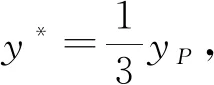
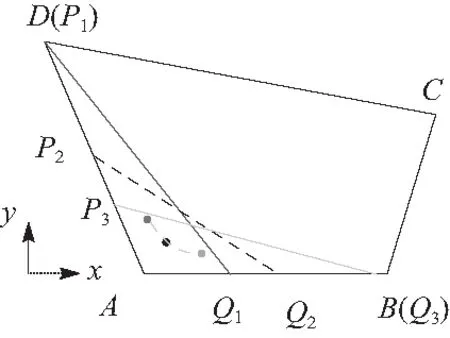
图4 四边形网格拆分出三角形网格的可能范围
3.2 拆分出四边形的情况
对于四边形网格拆分出2个四边形的情况,类似于3.1中的情况,首先进行旋转变换,使2个交点R、S分别位于AD边和BC边上;然后给定各点坐标数据,如图5所示.

图5 四边形网格拆分出四边形网格的示意图
由于没有一个确定的公式直接给出四边形形心,使用将四边形ABSR拆分成2个三角形ASR和ABS的方法,因此,子网格ABSR体积和形心分别为
(13)
求解方程组得到:
(14)
式中:
Δ=4V*2A,A=
符号±表示此时yS是正的,yS>yR,反之亦然.
将求出yS,yR代入式(13)可以得x*和y*之间的关系为
F4(x*,y*)=x*2-(k1+k2)x*y*+
(15)
根据二次曲线标准型不变量的性质[12],当k1=k2时子网格形心(x*,y*)轨迹曲线为抛物线;当k1≠k2时子网格形心(x*,y*)轨迹曲线为双曲线.
当k1≠k2时,实际形心(Px,Py)的最接近位置(x*,y*)应满足两点连线垂直于曲线在(x*,y*)点处的切线条件. 即:
(x*-Px,y*-Py)×
(16)
求解得到x*和y*关系后代回到式(13),化简得到
(HF2-36C2)y*4+(2FGH+F2J-72CD)y*3+
(HG2+KF2+2FGJ-72CE-36D2)y*2+
(JG2+2FGK-72DE)y*+(KG2-36E2)=0
(17)
式中:
H=9(k2-k1)2;
K=-[8V*(k2-k1)+3].
当k2≠k1时,HF2-36C2=36(k2-k1)2(k22+1)(k12+1)≠0,式(17)恒为4次方程,可以采用文献[13]的方法得到解析解,至多有4个实根. 又有式x*=f4(y*),故对每一个求出的y*,都可以求解出唯一一个x*.
k1=k2时,式(17)可以修正三次方程,可以采用文献[13]的方法得到解析解,至多有3个实根. 又有式x*=f4(y*),故对每一个求出的y*,都可以求解出唯一一个x*.
3.3 一般情况拓展
在2.3节中,推导了式(9)来计算五边形子网格的形心. 当凸四边形网格的A点位于五边形子网格中时,可以使用式(9)对图形进行适当的旋转以简化计算.
从几何角度考虑,当子网格体积V*>SΔABC时,可以选择对侧三角形DAC作为拆分三角形计算,也就是将点D平移至原点,将点C旋转并缩放至(1,0),之后进行计算. 总的来说,即选择三角形的第一个点为原点,第二个点为(1,0)点. 进行该情况的计算. 对于所有可能的情况,选择计算三角形如下:
V*>SΔABC时,选择ΔDAC求解;V*>SΔABD时,选择ΔBCD求解;
V*>SΔBCA时,选择ΔCDA求解;V*>SΔCDB时,选择ΔDAB求解.
4 界面重构算例
4.1 随机四边形网格中进行界面重构
在尺寸为1×1,网格数量为160×160的随机四边形网格中构建一个圆心为(0.5,0.5),半径为0.35的圆形,结果如图6所示,图6(a)为整体重构界面图,图6(b)为局部界面图.
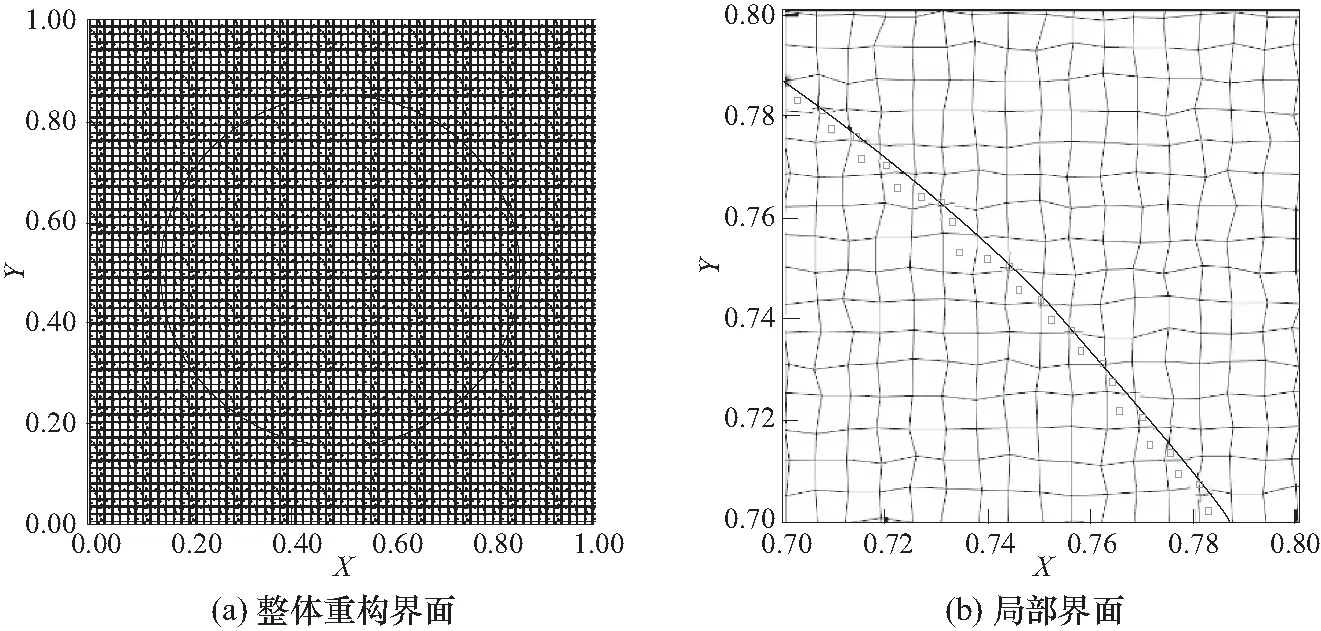
图6 圆心为(0.5,0.5),半径为0.35的圆在随机四边形网格中的重构
4.2 界面重构效率比较
本节采用重构同心圆的方法对传统Brent迭代方法和解析解求法的计算效率进行比较. 在[0,1]×[0,1]的网格上重构10个同心圆,其圆心均为(0.5,0.5),半径为0.05至0.5(间隔0.05). 在网格密度为30×30的情况下重构结果如图7所示,传统方法耗时47.95 s,解析解方法4.68×10-2s,计算效率提高了约1 000倍.

图7 采用传统及解析方法重构10个同心圆
将网格密度增加到500×500后,传统方法用时403.17 s,解析解方法用时0.36 s.
4.3 二维强激波冲击水中气泡
本节采用二维强激波冲击水中气泡算例[14],验证算法在应用中的稳定性及计算效率.
空气和水两种介质采用统一的状态方程[15],p=(γ-1)ρe-γB. 空气、静止的水及水中强激波的初始密度、速度、压力及状态方程参数取值为
式中:p为压力;ρ为密度(g/cm3);u、v分别为x、y方向的速度(cm/ms);γ和B为状态方程参数.
计算域选择为12.0 cm×15.0 cm,网格步长取0.1 cm;x<3 cm设置为强激波,参数取Ωs,设置圆心为(3 cm,6 cm),半径3 cm的圆形气泡,参数取Ωa,其余部分为静止水,参数取Ωw;计算域左侧设为入流边界条件,其余边界设为固壁有滑移条件.
典型时刻的密度梯度图像如图8(左为解析方法计算结果,右为传统方法计算结果):

图8 典型时刻的密度梯度图像
本文还对比了解析方法与传统方法的计算效率. 运行1 000步,传统方法MoF重构部分用时34 289.36 s;解析方法MoF重构部分用时26.83 s,计算效率提升显著.
5 结束语
本文基于MoF界面重构方法提出了一种适用于任意凸四边形网格的解析界面重构算法,通过分别讨论不同子网格拆分情况下的子网格形心曲线,解析地求解出界面重构的最小化问题,实现MoF方法界面重构,大幅提高了界面重构效率. 采用随机四边形网格内界面重构验证,证明了界面重构的有效性和准确性;采用激波冲击气泡的算例验证了算法在实际应用中的有效性和对计算效率的提高.
