轨道交通车辆单元制动器停放制动力补偿方案及其优化计算 *

虞晓峰，余毅权

(南京中车浦镇海泰制动设备有限公司，江苏 南京 211800)

0 引 言

轨道交通车辆须在无压缩空气状态下进行车辆停放制动，通常采用装备了储能弹簧的单元制动器进行停放力输出。由于单元制动器空间受限，须采用高应力、大载荷(刚度较大)的储能弹簧，该弹簧输出力值随工作行程的变大而降低。单元制动器在生产及使用过程中难免出现尺寸偏差、弹性变形、机械磨损、制动摩擦副磨耗补偿异常等造成储能弹簧工作高度不稳定的现象。因此，单元制动器的停放力值也常不稳定。笔者提出一种采用弧线代替传统直线作为楔形放大作用线并进行弹簧力值因行程影响导致降低而补偿的设计方法和具体计算过程，该方法可有效改善单元制动器停放制动力值不稳定的现象，达到设计目标。

1 作用原理

单元制动器作为轨道交通车辆的制动执行机构，其摩擦副间隙通常设置为3～6 mm。单元制动器具有磨耗自动补偿功能，正常情况下，其制动盘与闸片的间隙均稳定处于3～6 mm范围内，但实际使用过程中也存在偏离目标范围的情况，其间隙变化尤其对停放制动力影响较大。如图1所示，一种采用储能弹簧的单元制动器停放机构，停放缸排气释放弹簧，弹簧驱动楔形拉杆，垂向弹簧力值被楔形拉杆传递至横向的制动套筒最终传递给摩擦副产生停放制动。为充分利用车下空间，降低弹簧设计应力，通常采用楔形放大机构将弹簧输出力进行放大后使用。

图1 停放机构原理简图

传统方法是采用直线作为放大作用曲线，放大倍率即为1/tanθ(θ<90°)，θ为滚子与楔形拉杆接触点的切向角度(作用直线与垂直方向角度)，随着弹簧工作高度增大，弹簧力值降低(弹簧输出呈线性)，相应的放大机构输出力也随之降低。而采用弧线代替直线后，随着弹簧工作高度增大，切向角度θ变小，放大倍率1/tanθ将增大，对放大机构的输出力进行一定的补偿。但因为弹簧输出力在降低、放大倍率在增加，机构输出力的最终大小仍和作用曲线存在重要关联。因此，研究作用曲线及其作用效果显得十分必要。

2 输出力计算及优化分析

停放制动力的计算可根据机构设计的空间尺寸进行初步确定曲线参数，充分考虑机构弹性变形、尺寸偏差等影响因子，利用Excel工具进行公式化迭代计算，结合计算结果，反向计算曲线半径，采用CAD绘图几何方法进一步优化楔形放大机构的作用曲线，过程如图2所示。

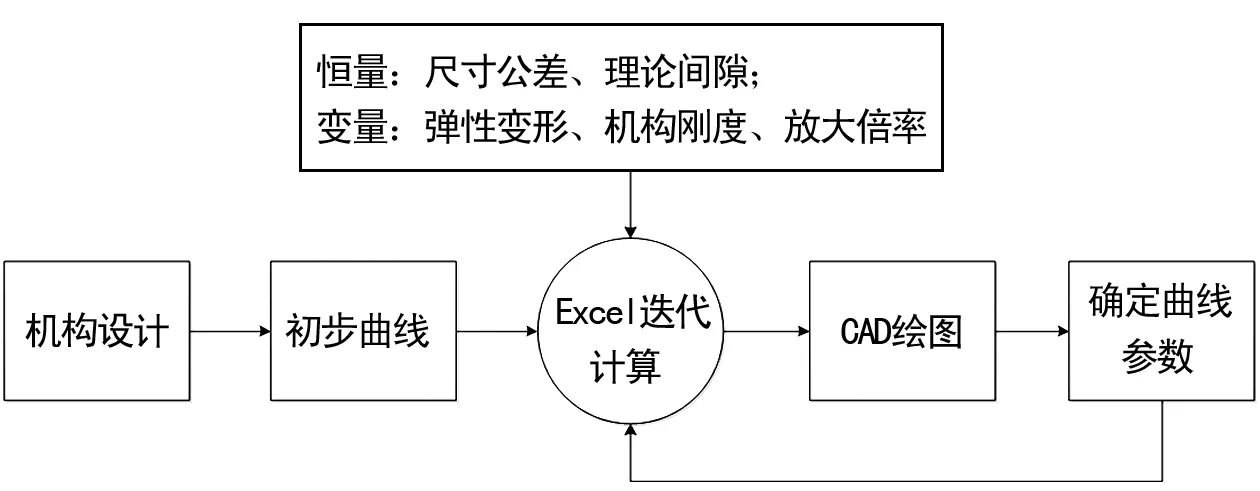
图2 计算过程

2.1 输出力计算

套筒滚子在楔形拉杆作用曲线上运动时，受力方向随着作用曲线变化而变化，作用曲线由Ⅰ段、Ⅱ段组成。为便于阐述过程，对作用曲线进行了几何尺寸标注和定义，如图3所示。

图3 几何关系图

(1) 放大倍率计算 为了缩短停放制动行程，楔形块设计为分段曲线，第Ⅰ段为快速制动行程，第Ⅱ段为工作行程，分界点为坐标为(x1，y1)，如图3所示。因快速制动行程非工作面，此处不进行分析。根据工作原理，x为停放制动行程，y停放弹簧伸长量，由几何关系楔形块的放大倍率i与停放制动行程x由如下关系：

当停放制动行程大于x1(mm)时，停放倍率表达式为：

(1)

(2) 弹簧伸长量 根据图3几何关系，停放制动行程x与停放弹簧伸长量y有如下关系：

当停放制动行程大于x1时，停放弹簧伸长量y表达式为：

(2)

(3) 输出力计算 将机构部件的尺寸公差累计间隙进行分析计算得到衡量值Δ1；

将机构部件进行有限元分析计算，可得出机构刚度δ，即可得到弹性变形Δ2，其与弹簧输出力Fw基本成线性关系，因此有：

Δ2=Fw×δ

制动器的缓解间隙S，停放制动行程x：

x=S+Δ1+Δ2

(3)

弹簧设计刚度k，对应的弹簧输出力为：

Fw=F0-y×k

(4)

当制动器处于理论间隙为S0(mm)时，停放制动行程x、弹簧的输出力Fw、放大倍率i三个参数相互影响，此处对式(1)～(4)进行迭代计算，即可确定Fw及i。

根据制动单元工作原理不难得出理论间隙为S0(mm)时停放制动力(α、β、γ为常数)：

FP=(FW+α)×i×β+γ

(5)

2.2 优化分析

由上述计算过程及结果可知，不同的理论间隙S0可算得出不同的x、Fw、i及FP。在产品设计中，优化目标是停放制动力值FP保持恒定，而FP保持恒定的关键在于作用曲线的设计。

在一款带停放单元制动器设计中，根据机构尺寸及空间，初步确定以下关键输入参数，见表1。

表1 初步确定参数

采用EXCEL工具将式(1)～(5)进行公式化，分别计算3～6 mm范围内(按0.1 mm递进)的Fw、i及FP，将计算结果进行图表化分析，如图4所示。

图4 停放制动力初步计算结果

由图4可知，既有作用曲线具有明显放大作用且具有一定补偿作用，但随着缓解间隙增大，停放制动力出现了小幅下降。

针对上述结果，结合图3几何关系，取优化目标停放制动力Fw值为50 kN恒定值(力值大小取决于车辆停放制动需求)，根据式(5)，可得出相应的放大倍率i值，再根据式(1)，即可计算出不同缓解间隙下的曲线半径R值。此时计算所得的R值可认为是目标曲线位置近似圆的半径。

借助于CAD工具分别以(缓解间隙初始值、中间值、最大值)3 mm、4.5 mm及6 mm时的y值作直线，确定停放弹簧工作高度。以三点不同位置对应R值为半径、圆心不变作圆，分别与三条直线相交形成3个模拟接触点，再分别以上述3接触点确定圆，该圆即为目标作用曲线的理论轮廓。重新量取作用曲线的参数，如表2所列。

将优化后的作用曲线参数带入上述计算公式进行输出力计算，不同缓解间隙对应停放制动力的结果如图5所示。

表2 优化参数取值 /mm

图5 优化后的停放制动力初步计算结果

对比图4、5，优化后的停放制动力明显增加，并且力值下降趋势明显改善。

3 结 语

上述关于轨道交通车辆单元制动器产品设计中补偿停放制动力衰减的设计方案及其计算方法,能够根据设计目标要求，考虑机构刚度、尺寸公差等多种影响因子，进行较为精确的停放制动力的计算，根据计算结果，采用几何方法进一步优化楔形放大机构的作用曲线。经过对产品停放制动力进行测试，结果表明随着缓解间隙的增加，停放输出力不再下降，补偿方案及优化计算明显有效。文中提及的方案及计算在类似产品设计中具有重要的指导意义。