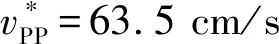基于边坡稳定性的临界损伤质点峰值速度研究
2021-05-18周文海
梁 瑞,包 娟,周文海
(兰州理工大学 石油化工学院,兰州 730050)
1 研究背景
在边坡开挖工程中,爆破开挖岩体和保留岩体稳定性这一相互矛盾的问题普遍存在[1-3]。爆破后的开挖岩体和保留岩体均存在不同程度的损伤,实际工程中需选用有效控制方式去分析爆破载荷作用下各区域的损伤特性。为确保施工的安全及边坡的稳定,人们将理论研究、数值模拟及现场试验应用于爆破前边坡临界破坏的判定[4-6]。
岩体损伤范围探究初期主要采用实地测试,且声波测试法效果最佳。朱传云等[7]和张国凯等[8]通过爆破载荷作用下测量爆前爆后的声波速度变化得到岩体的损伤范围。Singh等[9]和Lu等[10]研究指出质点峰值速度(Peak Particle Velocity,vPP)、振动频率和振动波传递形式均会造成爆破近区和边坡的动力响应;史秀志等[11]在大量边坡爆破工程研究中发现,爆区地表质点峰值速度与其周围环境的振动紧密相关。胡英国等[12]在大量边坡爆破损伤研究过程中,提出一种将边坡爆破岩体的损伤与振动进行耦合控制的方法,发现径向质点峰值速度最适合该控制方法,并且采用试验和模拟数据验证了该理论的准确性。Silva等[13]结合爆心距、质点峰值速度以及岩石的抗拉抗压强度确定岩体损伤范围。另有众多学者利用理论计算、实地试验及数值模拟研究确定岩石损伤范围和特征[14-15]。刘亮等[16]对白鹤滩工程项目开挖区进行大量声波试验,确定了岩体损伤阈值;费鸿禄等[17]利用声波测试法确定爆破载荷下边坡损伤效应,并结合强度折减法得到边坡爆破损伤对边坡安全系数的影响比爆破载荷影响更大。
总结边坡稳定性研究,发现前人利用动力响应研究在爆破载荷作用下边坡的位移、速度规律以及通过岩体损伤确定岩体弱化范围,另有基于自然状态下边坡稳定的安全系数研究,但就结合两者分析岩体边坡稳定性及岩体弱化规律的研究较少。本文首先采用有限元折减法确定所研究边坡的潜在滑动面,其次建立爆破载荷作用下的边坡单孔爆破模型进行数值模拟,将该模型计算结果与vPP经典判据进行比较,确定岩体损伤D的临界质点峰值速度以及vPP与爆心距l、岩石应力之间的关系,同时探究了爆破载荷作用下潜在滑动面近区监测单元的速度和位移变化规律。
2 静载状态下边坡有限元折减理论模型
有限元法在边坡稳定性评价中应用广泛,通过考虑岩土的应力-应变,对初始凝聚力与摩擦角迭代折减,直至数值模型受到破坏、岩体失稳,进而确定临界安全系数。本文选用摩尔-库伦(Mohr-Coulomb)屈服准则,取初始折减系数F=1.0,然后对边坡土体材料强度系数进行折减。公式为:
(1)
(2)
式中:C为岩土初始凝聚力;φ为内摩擦角;C′为折减后初始凝聚力;φ′为折减后的内摩擦角;F为折减系数。
以选取西北某矿区开采边坡为原型进行数值模拟,坡面高度9.45 m,坡面角41°,根据现场地质资料选取材料,岩土体以弹塑性为主。主要参数见表1。

表1 边坡模型岩土参数
当滑动面塑性应变发生突变且有限元的数值模拟计算结果不收敛,则认为此滑动面已失稳[18]。根据式(1)、式(2)进行强度折减计算,计算结果汇总如表2所示。

表2 折减算法结果
依据表2计算结果,提取4个不同折减系数的边坡塑性应变云图,如图1所示。

图1 不同折减系数下塑性应变云图
图1中4个不同折减系数的塑性应变云图给出该边坡潜在滑动面由开始破坏到临界破坏再到完全破坏的整个过程。折减系数F=2.8时,潜在滑动面处于临界破坏的状态,F=3.0时,有限元计算结果不收敛,塑性变形已完全贯通,边坡遭到破坏。
3 单孔爆破模型建立
炮孔模型的尺寸、选材都与上述某矿区静载状态下折减模型一致。取弹塑性岩土体进行单孔爆破数值模拟,涉及3部分:炸药、空气、岩石。炸药选取2#岩石乳化炸药,其材料类型为HIGH_EXPLOSIVE_BURN。炸药状态方程选取不考虑炸药产物成分的JWL方程[19],具体形式见式(3)。其中A、B、R1、R2、ω为材料参数,E0为初始内能,P为压力,V为相对体积。具体参数如表3[20]所示。
(3)

表3 炸药主要参数[20]
空气选取MAT_NULL模型,选用空气的控制方程为EOS_LINEAR_POLYNOMIAL线性多项式方程,具体形式见式(4)。
P=(C0+C1μ+C2μ2+C3μ3)+
(C4+C5μ+C6μ2)e。
(4)
式中:C0—C6为0~6项多项式系数;μ为体积比;e为单位体积内能。空气主要参数见表4[20]。

表4 空气主要参数[20]
岩石材料为弹塑性材料,选用流动强化准则MAT_PLASTIC_KINEMATIC。岩体参数见表5。

表5 岩体参数
边坡爆破采用深孔爆破,炸药孔深12 m,孔径为150 mm,岩体选用LAGRANGE算法,炸药、空气选用ALE算法,并将炸药与空气设为多物质组与岩体进行流固耦合控制。本文数值模拟采用SOLID164单元,划分网格后单元数为173 600个,边坡模型左右边界施加x方向位移约束,底部施加x、y方向位移约束,边坡整体施加重力加速度并添加非反射边界条件。单孔爆破下不同时间的塑性形变云图如图2所示。
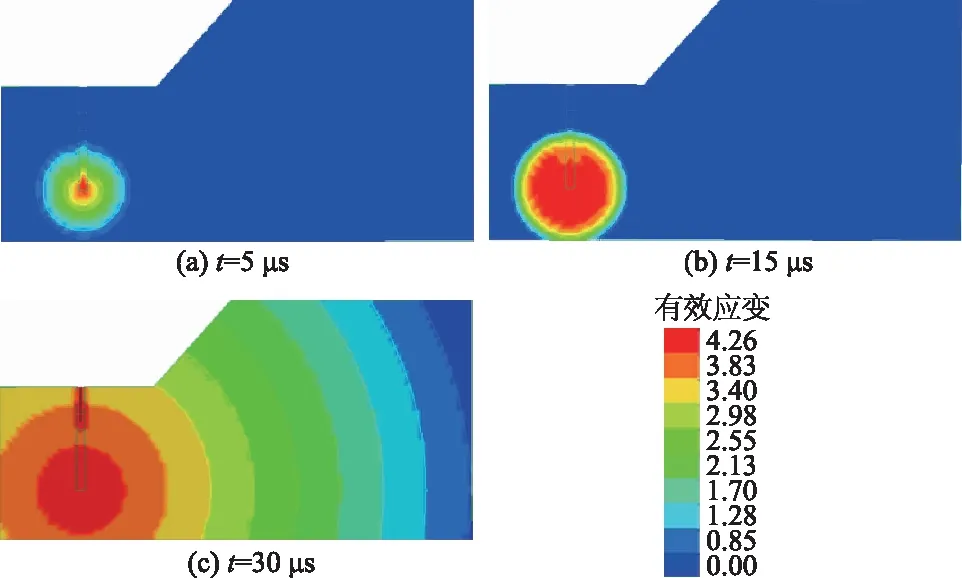
图2 单孔爆破下不同时间的塑性形变云图
4 岩体爆破近区vPP的确定
4.1 损伤定义
实际工程中常用损伤(D)表征岩石微观单元的破坏程度,并多采用岩石破坏前后宏观参数的比值定义[16],见式(5)。
(5)
式中:E0、E分别为爆破前和爆破后岩体的弹性模量;v0、v分别为爆破前和爆破后岩体的波速。
4.2 基于最大应力的vPP损伤判据
当今广泛使用的vPP损伤判据是最大拉应力理论[12],即
(6)
式中:CP为岩体纵波速度;[ε]为岩体极限拉应变;E为岩石弹性模量;[σt]为岩石的抗拉强度。
岩石边坡的爆破范围控制主要取决于当层台阶的轮廓损伤深度,因此有必要研究轮廓面保留岩体的损伤区形成的力学机制,该研究可为爆破振动安全控制标准的建立提供理论依据。图3是本文边坡爆破模型中损伤区外沿轮廓上某点的径向应力、环向应力以及竖直向应力的时程变化曲线。爆破过程中径向和环向应力峰值明显大于竖直方向应力峰值。岩体的破坏主要来自径向应力波产生的动力响应,次要破坏为环向破坏,竖直方向的破坏由炸药起爆后应力波的反射即二次应力波的动力响应造成,故竖直方向应力与岩体损伤关联较小。考虑径向和环向的影响,根据图3曲线将岩体受力划分为4个阶段:径向-环向受拉、径向受拉-环向受压、径向-环向受压、径向受压-环向受拉。径向与环向同时受拉阶段爆破能量较小且衰减迅速,并不能使岩体发生损伤破坏;径向受拉-环向受压、径向受压-环向受压阶段岩体受力均超过岩体动载抗拉强度,岩体产生损伤拉裂;径向受压-环向受拉阶段拉压应力均远小于动载拉压强度,不会造成岩体损伤。经分析,得到造成岩体损伤的主要原因是径向拉应力和环向拉应力,径向拉应力的峰值远大于环向拉应力,故在研究岩体损伤特性时,径向拉应力是最主要的影响因素,因此文中将径向拉应力作为最大拉应力。

图3 不同方向的应力时程曲线
如图3所示,边坡实际爆破过程中,所受应力比式(6)理论考虑的应力复杂,本文只考虑径向拉应力的影响。研究爆破岩体近区各向应力的变化有利于实际爆破工程中安全标准的制定。

表6 岩石爆破损伤的质点峰值振动速度临界值[21-22]
4.3 炸药近区vPP与爆心距的关系
基于文中边坡实例数值模拟结果,在炮孔附近保留岩体中,在距离炮孔5 m范围内的同一水平面上取不同爆心距处单元作监测点,如图4所示。绘制爆破近区vPP随爆心距衰减规律曲线,如图5所示。
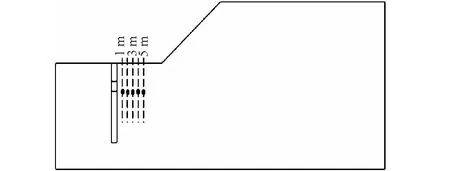
图4 爆心距监测点示意图
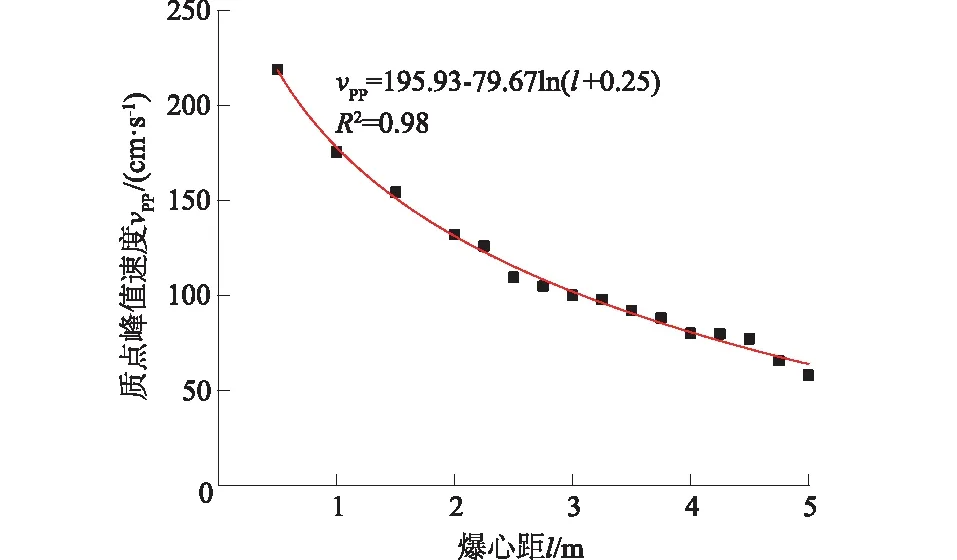
图5 爆破近区vPP随爆心距衰减曲线
由图5可以看出,在保留岩体中,随着爆心距增大,vPP以对数函数趋势迅速衰减,爆心距越小,速度衰减越快。本文数值模拟选用孔底爆破,故炸药柱底部的速度大于炸药柱顶部的速度。
Bauer等[21]和Savely[22]依据声波实测和爆前爆后新增裂隙的调查等方法提出爆破损伤vPP判据,见表6。
胡英国等[12]通过研究发现当vPP>60.8 cm/s时,岩体损伤量D迅速升至0.8;当vPP>110.0 cm/s时,损伤量D=1,岩体完全损伤。唐红梅等[23]通过研究发现,当爆心距l<1.09 m时,岩体处于粉碎区和碎裂区,0.9<损伤变量D<1.0,岩体碎裂,有大量裂隙,无法自稳;当1.09 m 由图5中的数据和经典判据中的经验数据可知:在本实例中,当vPP>63.5 cm/s时,岩体达到损伤速度阈值,爆心距l=4.96 m。随vPP的继续增加,损伤的程度持续加深,当63.5 cm/s 结合图3岩石实际爆破时复杂的三向应力以及前人研究[7,12,16]可知,质点峰值速度不仅与动拉应力有关,还与爆心距、炸药量、装药方式等有关。式(6)中质点峰值速度和动拉应力为正比关系,所得vPP误差较大,且因建立爆破近区岩体受力状态和破碎程度的数值关系十分困难,因此尝试探寻岩石动拉应力峰值与vPP的统计关系。 图6 动拉应力峰值与vPP统计关系 有限元折减法得到的边坡折减滑动面及其应力等值面示意图如图7所示,取爆心距分别为11.0、12.5、14.0、15.5、17.0 m的5个平面与折减面(A、B)及其近区应力等值面(C、D、E)的交点作为监测点,探究边坡潜在滑动面位移与速度变化规律。 图7 边坡折减滑动面及近区应力等值面示意图 如图7所示,分别在5个研究面(A、B、C、D、E)上取5个代表监测点,通过数值模拟,得到不同监测点的位移、速度峰值,得到不同应力等值面监测点的爆心距-位移变化及爆心距-速度变化,如图8所示。 图8 折减滑动面及其应力等值面位移和速度变化曲线 由图8可知,折减面A与折减面B监测点的位移与速度的变化规律基本一致,均随爆心距增大先增大再减小,可知监测点的位移和速度变化不单与爆心距的改变有关;爆心距为14 m处折减面A、B的位移均达到最大值,由于折减面的滑移,折减面B的位移突变明显。因折减面A、B距离炮孔高度差更大,折减面A、B的位移与速度较等值面C、D、E整体偏小。等值面C的位移和速度大致呈现随爆心距的增大而减小的趋势,在爆心距为17 m处有小幅增大;等值面D、E的速度和位移的变化规律仅与爆心距有关,随着爆心距变大,质点的位移变化明显变小,速度也迅速衰减。 综上可发现,距离折减面越远的等值面上质点的速度和位移随爆心距增大而减小;折减面及距离折减面越近的等值面上速度和位移的变化并不随爆心距增大而减小。在实际工程中,通常可以通过监测边坡潜在滑动面上岩土的振动速度和位移,对存在滑移可能性的边坡实施安全防护。在防护过程中,爆心距等单一因素不能作为判断边坡安全的指标。 (1)通过对临界安全系数F=2.8的边坡进行单孔爆破数值模拟,得到爆破近区岩体损伤速度阈值为63.5 cm/s。当63.5 cm/s<质点峰值速度vPP<127.0 cm/s,2.12 m<爆心距l<4.96 m时,岩体处于裂隙区;当质点峰值速度vPP>127.0 cm/s,爆心距l<2.12 m时,岩体进入粉碎区。 (3)边坡折减面处质点的速度和位移小于折减面近区应力等值面处质点的速度和位移。且随爆心距的增大,边坡潜在滑动面塑性破坏区的位移与速度先增后减,未发生塑性破坏的应力等值面处的位移和速度逐渐减小。 本文研究了爆破近区vPP阈值,但对更大爆破范围的vPP变化规律未做出深入研究。4.4 临界损伤vPP的确定与讨论


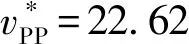

5 潜在滑动面近区位移与速度规律分析


6 结 论