高考立体几何空间角解题技巧探讨
2021-05-18陈伟坚
陈伟坚
广东省连州市连州中学 广东 连州513400
1 引言
高中数学教学中,对学生数学核心素养的培养是通过学科教学来引导学生用数学的眼光观察世界,能够用数学思维来思考世界,并学会用数学语言表达世界。在高中数学中,立体几何是重要的一部分内容,通过立体几何教学来培育和发展高中生的数学学科核心素养是有效的途径。近几年的高考试卷中关于立体几何的题目类型呈现多样化特征,有选择题、填空题、解答题,既包括对空间几何的概念、空间想象能力和运算能力的考察,还包括对线线关系、线面关系和面面关系等逻辑推理能力的考察。在立体几何题目中,空间几何角计算是近几年高考立体几何的必考内容之一。这部分内容既是重点又是难点,每年山区连州考生在这部分题目中整体得分较低。为了帮助高中生更好地掌握和解决立体几何空间角问题的能力,本人对这部分内容进行了分析和研究。
2 空间角例题分析
例题1(2019高考全国Ⅲ卷理数):图1所示为矩形ADEB,Rt△ABC和菱形BFGC组成一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿着AB,BC折起使得BE与BF重合,连接DG,得到图2。
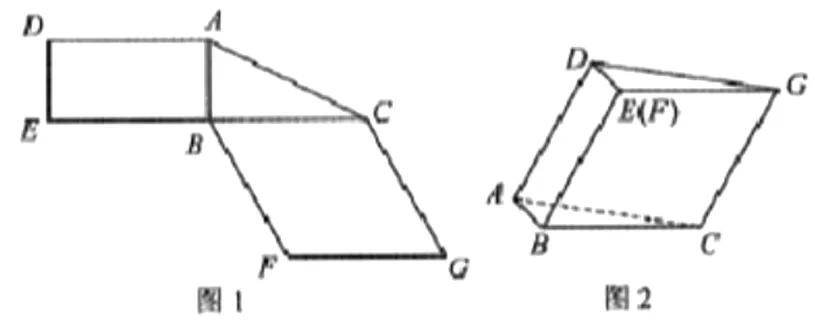
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角B-CG-A的大小。
例题解析:
(1)根据已知条件可以知道AD//BE,CG//BE,因此可以得到AC//CG,故AD和CG两条平行线可以确定一个平面,即A,C,G,D四点共面。
根据题目条件AB⊥BC,AB⊥BE,因此AB⊥平面BCGE。又因为AB∈平面ABC,因此可以得到平面ABC⊥平面BCGE。


因此,二面角B-CG-A的大小为30°。
例题1考察了多面体折叠,学生需要考虑在折叠的过程中变化的量,以及不变的量,然后通过建立坐标系,采用向量解法将二面角转化为二面角的平面角进行求解。
3 一题多解方法探究
在立体几何空间角的解题过程中,通常可采用不同的解题思路和方法。以二面角大小求解为例,通常可分为两种情况,一种情况是直二面角,另一种情况是非直二面角。
当二面角是直二面角时,一般是采用几何求证来解题,依据是直线与平面垂直的判定定理,通过确定面面垂直来得到所求的二面角的大小。
当二面角是非直二面角时,可采用以下几种方法进行解题。
第一种方法是利用二面角的定义,即通过证明某角为二面角的平面角。通常题目中找不到现成的,因此一般需要通过三垂线定理做辅助线,然后再计算。
第二种方法是利用二面角的余弦值来进行解题。只要找到射影图形并计算出某一个半平面在另一个半平面的射影面积和该平面面积的比值,即计算出二面角的余弦值。这种方法计算量较大,但是不需要找出两平面的平面角。
第三种方法是先找出二面角的一个面内一点到另一个面的垂线,然后利用三垂线定理作出平面角,直接找不到垂线需要根据题目已知条件作出点到面的垂线。
第四种方法是利用向量来求解,这是相对万能的一种方法,是上述传统解题方法的补充,通常在一些无从下手比较困难的二面角解题中应用。在实际的应用中,向量法又可以分为两种情况。一种情况是先做出二面角的平面角,然后利用向量的内积公式来进行解题。另一种情况是分别做出两个半平面的法向量,然后根据向量夹角公式进行解题。解题中,学生们要注意向量夹角不一定是二面角,还可能是二面角的补角。
4 结语
如今,新课程改革已经全面进入实施阶段,高中数学教学必须仅仅围绕核心素养培养的理念,以发展学生数学学科核心素养为导向实施教学。本文结合高考例题对高中立体几何空间角这一重点和难点进行了分析研究。通过用一题多解的方法帮助高中生建立空间思维,使考生能够在面对这部分题目时能更顺利地解题,提升学生的数学核心素养。通过对立体几何的学习,引导学生建立数学思维,用数学的知识规律来解决问题。
