余热回收器换热管与管板胀接过程残余接触应力及密封性能研究

吴倩倩 董金善 胡国呈

（南京工业大学机械与动力工程学院）

我国工业领域能源消耗量约占全国能源消耗总量的70%，由此在工业领域的节能减排和能源回收利用可带来显著的经济效益和社会效益。相关研究表明：在工业生产过程中会产生大量的余热或废热，而这部分能源的回收效率不足35%。因此，工业余热的回收利用被认为是一种“新能源”，面对如此巨大的节能潜力，实现工业余热回收是节能减排的重要内容［1］。 烟气余热回收器工作场景较为严苛，也因此会在多种可能因素下发生不同种类、不同表现的设备失效，而各个构件的连接处则为易发生失效的部位［2］。 江小志等的研究表明，基于ANSYS的分析设计方法可很好地应用于有温差应力存在的管板设计中［3］。 Sui R J等的研究发现，在制造过程中，若管板与换热管的胀接压力小于消除间隙所需要的压力时，在管孔与换热管间隙处易发生氯离子的富集并在高应力作用下会发生应力腐蚀［4，5］。 Liu L等对管壳式换热器管板焊接接头的失效分析表明，换热管与管板之间的焊接缺陷和胀接位置不合适，可能导致初始裂纹的形成［6］。GB/T 151—2014《热交换器》规定换热管与管板的连接方式有胀接、焊接和胀焊并用3种方式［7］。 前人的研究显示，液压胀接完成后，换热管与管板连接处存在胀接残余应力，是易发生泄漏失效、应力腐蚀的薄弱区域［8～10］。 因而，研究换热管与管板的胀后残余应力及其密封性能十分必要。

为了系统地研究换热管与管板连接接头的性能，对于换热管胀接工艺而言，首要确定的就是胀管压力的选择。 Goodier J N和Schoessow G J首次提出以带圆孔的无限大圆板替代实际的多孔管板进行分析，得到了胀管的残余接触应力和变形［11］。 Krips H和Podhorsky M将换热管与管板等效为两个同心圆的套筒模型，胀接过程等效为套筒的受力变形过程，并在此基础上提出了基于胀接压力的计算公式［12，13］。 国内的学者也对此进行了相关研究，颜惠庚等在假设材料为理想弹塑性材料的前提下， 基于Von Mises 应力准则，以单管等效胀管模型来分析换热管的胀接过程，并提出理论上满足换热管胀管性能要求的胀接压力计算公式［14］。 匡良明根据静压胀管原理，以单孔等效胀管模型提出了最佳胀管压力的概念，并将垫片密封的概念应用于胀管接头［15］。 随着计算机技术和有限元法的应用拓展，丁宇奇等以换热管与管板的胀接区域为研究对象，对该区域进行三维建模并采用非线性接触分析的方法，分析了不同胀接压力、开槽参数等对胀接区域残余接触应力的影响［16］。 李涛和段成红建立了换热管胀接区域的三维模型， 并模拟分析了贴胀和强度胀接，将理论解和有限元分析解进行对比，认为有限元解更加准确［17］。

1 液压胀接过程的研究背景

研究对象为某公司余热回收器，换热管与管板连接处发生了疑似应力腐蚀导致的泄漏失效。漏点试样剖面宏观照片如图1所示。 由图1可见，该余热回收器换热管与管板之间存在间隙，即换热管与管板的胀接过程未达到工程要求。

图1 漏点试样剖面宏观照片

2 液压胀接过程的理论分析

确定胀接区域的胀接压力可以更系统且有针对性地对胀接接头进行有限元模拟。 笔者采用颜惠庚等提出的计算方法，计算模型选用单管模型（图2）。

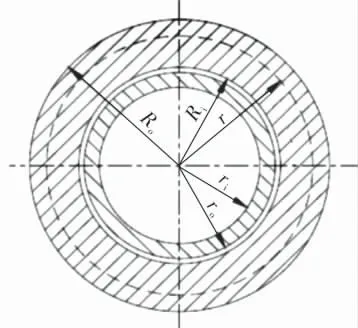
图2 液压胀接接头单管模型

设定换热管与管板均为理想弹塑性材料、遵循Von Mises屈服准则并忽略胀接过程中连接接头的轴向应力，分析过程有3个阶段：

a. 换热管的变形阶段。 胀接压力逐渐加载，在内压作用下换热管内壁发生完全塑性变形直到与管孔内表面接触，这个过程中管板不受力不变形。

b. 管板的变形阶段。 胀接压力继续升高，接触开始发生在管板与换热管间，管板也逐渐开始发生变形，并逐渐由弹性状态进入屈服状态。

c. 压力卸载阶段。 当胀接压力达到预先设定的值后，胀接压力就开始逐步卸载，换热管与管板均发生回弹，由于管板的回弹量大于换热管的回弹量，从而获得残余的接触应力。

换热管变形阶段，胀接压力：

式中 c——系数；

Ks——管板的外径与内径比；

Kt——换热管的外径与内径比；

Rc——塑性区半径；

Ri——单管套筒的内半径；

Ro——单管套筒的外半径；

σss——管板的屈服应力；

σst——换热管的屈服应力。

3 有限元数值模型的建立

3.1 几何模型

余热回收器的布管方式为正三角形排列，换热管与管板胀接结构如图3所示。 采用七孔模型［18］作为研究对象，并根据对称性选30°（360°/12）的范围。换热管长150mm，换热管外径16mm，管板厚度32mm，换热管壁厚4mm，管孔间距48mm，换热管外径与管孔间隙0.2mm， 因为该连接接头实际上是先焊接后贴胀，主要研究胀接过程，因而将焊缝处忽略并保留设计图中不胀区11mm的设置，建立管板孔无槽胀接模型。

3.2 单元类型选取

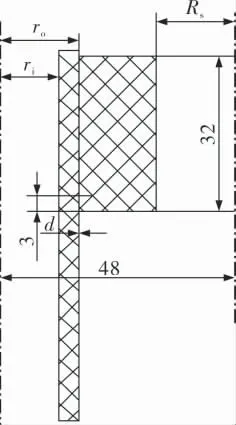
图3 换热管与管板胀接结构示意图

换热管与管板胀接过程属于高度的非线性行为，涉及几何非线性、材料非线性和接触非线性。 笔者基于ANSYS软件研究的胀接接头有限元模型结构实体单元选用solid95。 接触对的构建选用Target170目标面单元，Contact174接触面单元。摩擦系数设置为0.2， 求解方法选择完全的Newton-Raphson计算方法，打开大变形开关，激活自动时间步和线性搜索以加快求解。

3.3 材料特性

余热回收器管板材料为16Mn，换热管材料为Q345D。管板与换热管的材料性能接近，为方便理论计算与有限元模拟过程, 两者材料均取16Mn，其材料性能见表1，力学特性曲线［17］如图4所示，胀接过程中采用多线性随动强化模型Kinh来模拟胀接过程中的材料行为。

表1 两种状态的材料性能

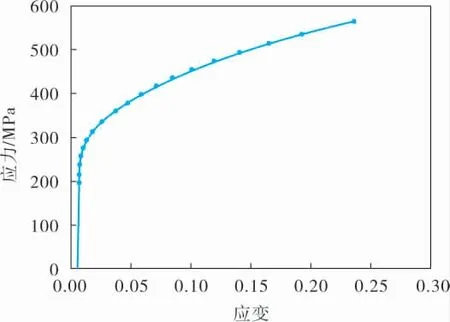
图4 16Mn的力学特性曲线

3.4 有限元模型

采用ANSYS APDL参数化建模直接在软件中构建实体模型的方式， 可以快速高效建立模型、修改相关参数，并完成网格划分。 有限元模型如图5所示。

设置约束条件：对称面施加对称约束；换热管下表面与管板下表面施加轴向位移约束；其余面为自由表面。 换热管与管板胀接过程的有限元模拟分为两个载荷步：一是在换热管内表面胀接区域面施加胀接压力；二是在该面上施加0MPa压力。 用两个载荷步来模拟换热管与管板胀接过程中的加压与卸载压力过程，并在两个载荷步中设置若干载荷子步。

图5 胀接结构有限元模型

4 胀接过程理论解与有限元解的结果分析

获得较高的胀后残余接触应力是采用液压胀管的目标，胀接接头有较高的胀后残余接触应力可以使得接头起到密封作用，隔绝壳程循环水对胀焊接头的影响。

4.1 胀接理论公式计算

依据前述的理论公式，并结合该余热回收器管板的胀接结构参数，可以得到理论计算参数值为：

换热管的外径与内径比Kt1.333

管板的外径与内径比Ks1.963

系数c 0.244

换热管屈服强度Relt320.0MPa

管板屈服强度Rels325.0MPa

最小胀接压力Pimin207.0MPa

有塑性变形时的胀接压力Pisy243.0MPa

最大胀接压力Pimax355.4MPa

4.2 有限元分析的有效性验证

由于理论公式的推导前提是假设材料为理想弹塑性，因而并未考虑常用工程材料的强化作用；并未考虑初始间隙影响。 而本次模拟的换热管材料（16Mn）强度较高且壁厚t=4mm，材料强化作用会对理论计算的结果产生较大影响。 为削弱理论假设带来的偏差，模拟中将换热管的壁厚设置为2mm，以验证有限元非线性分析用以模拟胀接过程的可行性，并确保相关参数的合理设置。

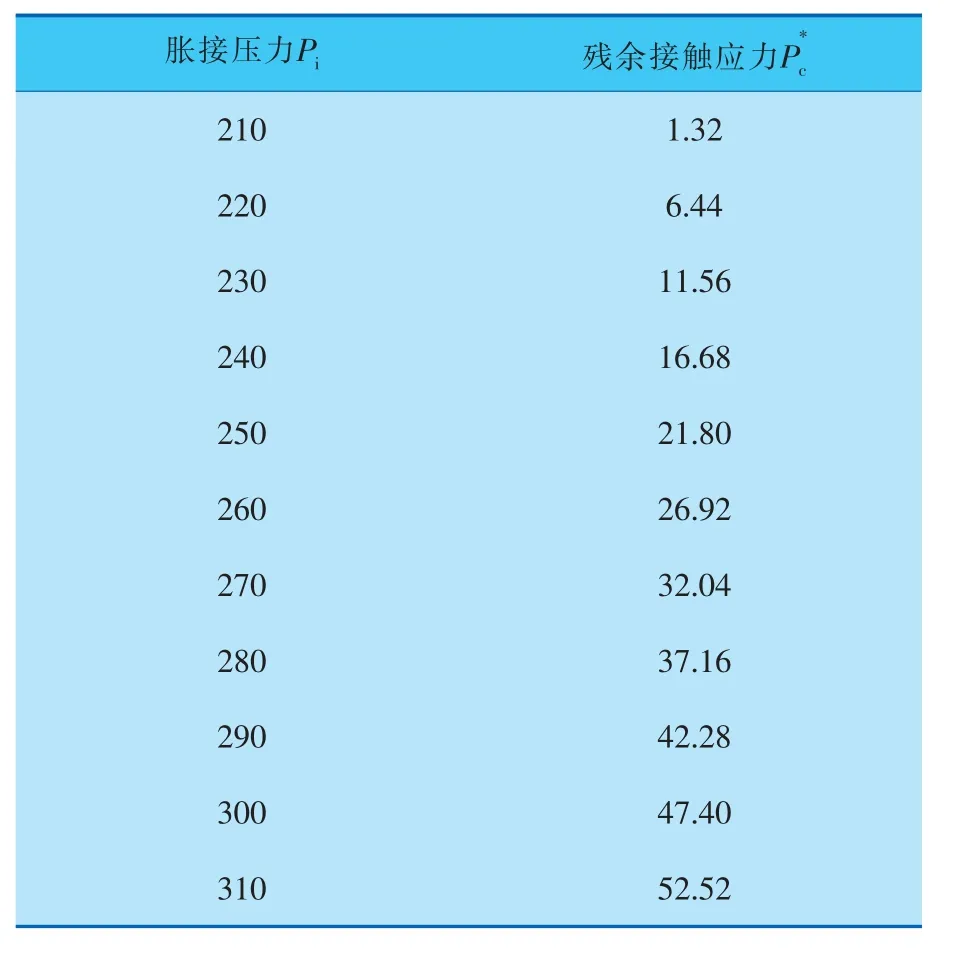
表2 液压胀接残余接触应力理论解 MPa

胀接过程是高度的非线性接触问题，因此接触刚度FKN的设置是否合适显得非常重要， 接触刚度较大时计算结果更加准确，但接触刚度过大也会引起总刚度矩阵的病态而不收敛。 本节的结构实体单元选择为solid95， 摩擦系数设置为0.2。FKN 值 分 别 取0.1、0.2、0.3 在 胀 接 压 力190 ～270MPa下进行有限元计算，提取有限元的计算结果中接触面的残余接触应力（图6）。

由图6可知， 接触刚度等接触条件对于接触非线性计算结果的精度影响很大，但在合理设置相关参数后，可以在液压胀接过程中使用有限元的非线性分析替代理论分析，并且在一定的阈值内有非常高的精度， 具体到本例是胀接压力为230MPa之后的有限元解和理论解都有很好的一致性，这也证明本模型的建立与边界条件的设置与网格的划分均较为合理。

4.3 胀接过程理论解与有限元解的结果分析

4.3.1 强度胀压力范围的残余接触应力

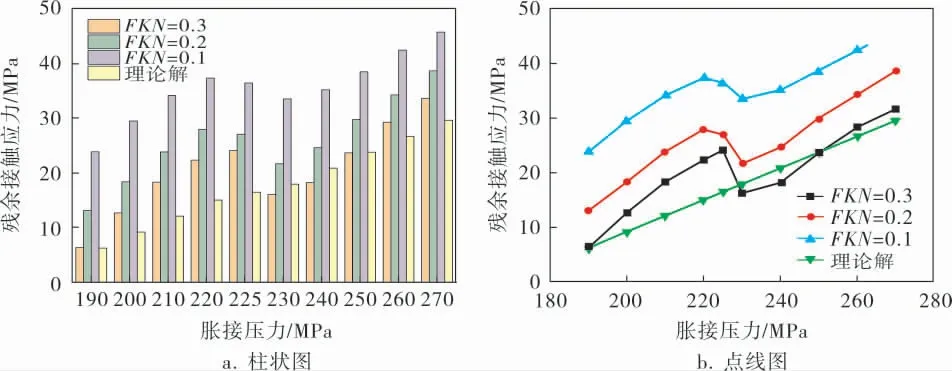
图6 不同FKN值下残余接触应力

t=4mm时换热管的胀接接头模拟结果如图7所示， 由图7和表3可以看出， 当胀接压力达290MPa以上时，理论解与有限元解有较好的一致性，而这之前偏差较大。 理论计算t=4mm时，管板孔内壁的屈服压力为243MPa， 提取胀接压力为280～310MPa，FKN=0.3的第1个载荷步加压后管板区域的应力值，结果如图8所示。 由图8可以看出，管板孔内壁屈服时胀接压力在290～300MPa之间，即290MPa以上时理论解与实际情况就较为一致。 所以计算结果也较为符合，290MPa以下时的理论解与有限元解偏差原因是：理论推导过程中认为管孔内壁已经屈服了，而实际上管板孔还远远没有达到屈服， 因此两者结果出现较大偏差，即换热管材料的强化作用将达到管板孔内壁屈服时的胀接压力提高了约50MPa。

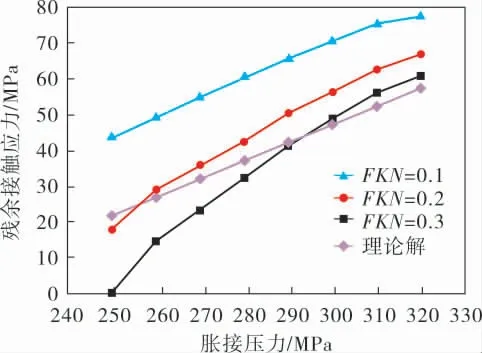
图7 不同FKN值下残余接触应力

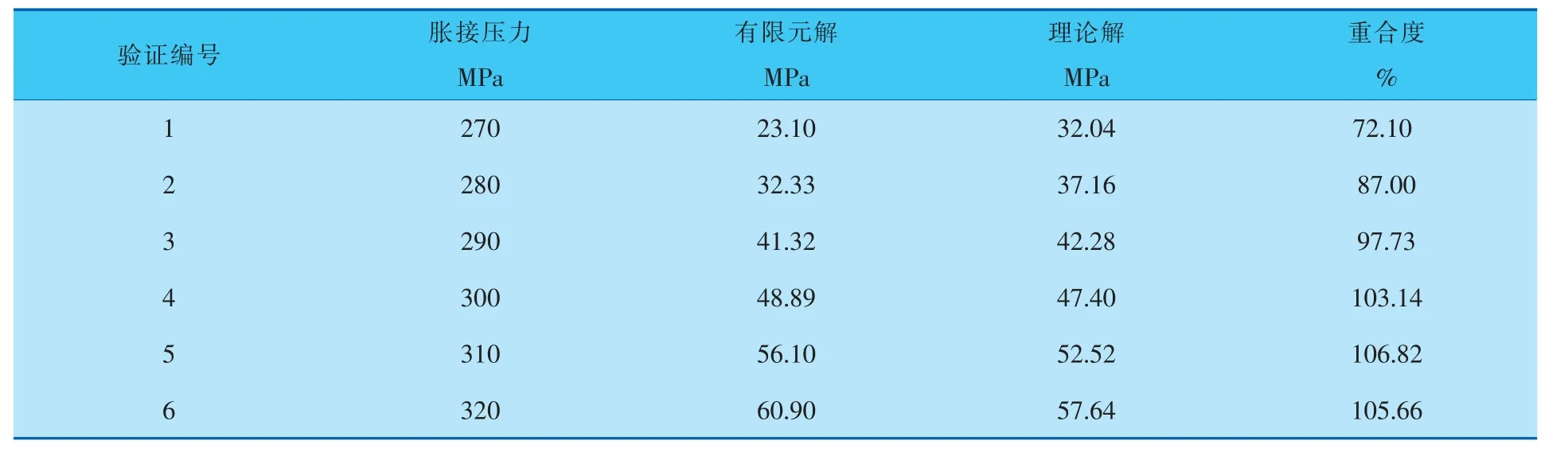
表3 不同胀接压力下理论解与有限元解比较

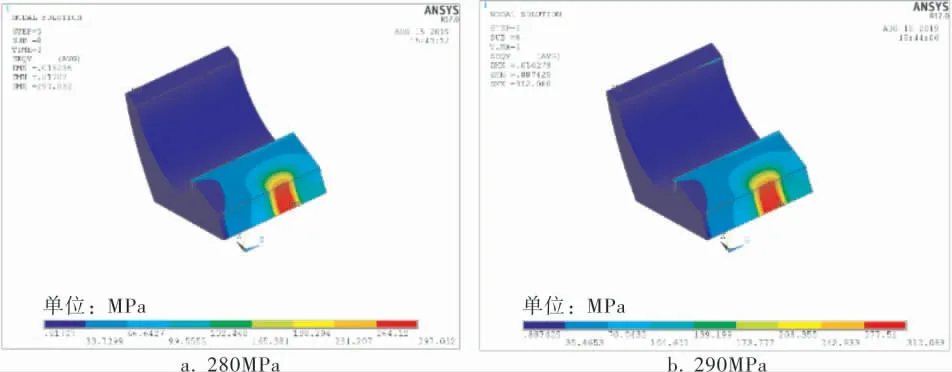
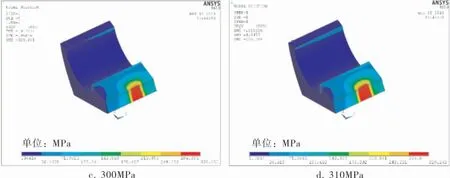
图8 不同胀接压力时管板的应力云图

4.3.2 贴胀压力范围的残余接触应力

t=4mm时， 理论计算值给出的贴胀压力范围为207～243MPa。 有限元计算结果表明，255MPa时接触面残余接触应力为7MPa（图9），而250MPa时残余接触应力为0。由此，笔者认为t=4mm时，实际的贴胀压力范围为255～300MPa。最小贴胀压力为255MPa,有限元解比理论解的最小贴胀压力提高了48MPa，误差为23%，显然由于壁厚增加，换热管材料的强化作用对理论解造成的误差变大了。并且导致理论推荐的贴胀压力范围内即使取最大值243MPa,接触面也没有残余接触应力即换热管与管板还未接触， 达不到贴胀预期设定的要求。

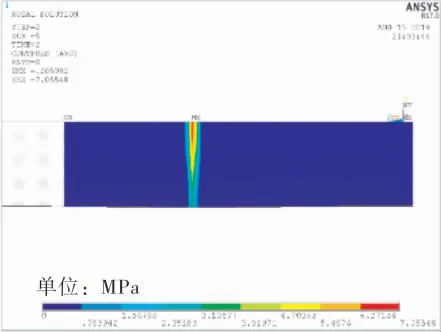
图9 胀接压力255MPa时残余接触应力云图

5 失效余热回收器换热管与管板密封性能研究

失效分析认为余热回收器发生泄漏的原因是应力腐蚀，换热管与管板之间存在间隙提供了壳程介质进入焊接接头处的通道。 本节针对这一结论进行验证。

该余热回收器换热管与管板接头采用的是先焊接后胀接，并且决定接头密封性能的是胀接后接触面的残余接触应力。 由理论计算给出贴胀压力的推荐范围为207～243MPa。 由前文可知，余热回收器换热管壁厚为4mm，即使选用最大的贴胀压力243MPa换热管与管板也没有发生接触，即没有残余接触应力。 胀接压力为250MPa时候，换热管外表面节点在x方向即径向位移最大值为0.199 48mm，即换热管与管板没有发生接触。

在判断胀接接头是否满足密封要求时，将密封环带类比于法兰连接中的金属垫片密封：施加胀接压力时换热管发生弹塑性变形与管板孔内壁贴合，卸载压力后由于两者变形回弹量不同从而产生残余接触压力作为初始垫片比压，用以阻止泄漏。 引入法兰密封性能的相关参数最小预紧压力y与垫片系数m。 y值表示迫使垫片变形和压紧面贴合以形成初始密封条件时垫片所需的最小压紧载荷，垫片系数m表示在操作状态时，为了达到密封不泄漏效果，垫片上所必须维持的比压与介质压力的比值。

为了简化问题，不予考虑在操作条件下密封环带接触应力的变化问题。 胀管模型的系数m由GB/T 150—2011《压力容器》查得为5.5，余热回收器壳程工作压力为5.5MPa，即要求残余接触应力不小于30.25MPa。 由此可知，该余热回收器在制作状态和水压试验时，该换热管与管板的胀接接头不能满足工作状态下的密封要求，在壳程压力作用下壳程介质可沿换热管与管板的间隙进入焊缝接头处。

6 结论

6.1 将理论公式求解与有限元非线性分析得到残余接触应力进行对比发现：在胀接压力较高即强度胀接压力范围内时，有限元解与理论解有很好的一致性，但在胀接压力较低时，两者误差较大，有限元分析结果更加合理。

6.2 换热管材料强化作用使得实际胀接过程中让换热管产生足够大的变形所需要的胀接压力增大。 也使得让管板孔内壁的屈服的胀接压力大于理论计算值；换热管管壁厚度越大，材料强化作用越强且理论计算结果与有限元计算结果的偏差越大。

6.3 在理论计算给出的贴胀压力范围内，不能满足接头密封性的要求。 实际上即使使用最大贴胀压力的情况下， 换热管与管板间仍然存在间隙。壳程介质能够在壳程压力作用下进入焊接接头处， 并在高温的作用下造成局部的碱液浓缩，最终导致应力腐蚀的发生。 因而，在有间隙腐蚀倾向且可能发生应力腐蚀的场合，建议选用强度胀接保证密封的可靠性。