基于轨迹特征圆的平面四杆机构标准化处理方法

李 磊， 彭其飞， 孙建伟*, 李晓东

(1.长春工业大学 机电工程学院， 吉林 长春 130012;2.中国第一汽车股份有限公司蔚山工厂， 吉林 长春 130011)

0 引 言

四杆机构在各种机械和设备中被用作执行机构，通常需要对特定任务有用的四杆机构连杆轨迹进行综合。在轨迹生成中，目标是让物体沿着指定空间路径曲线移动。轨迹综合的目的是确定连杆的长度和机架安装位置，使得连杆上的一点产生所需要的运动轨迹曲线[1-4]。国内外多位学者经过几十年的研究，提出许多有效、精确的设计方法用来综合四杆机构的轨迹[5-12]，其中使用数值图谱法和近似综合法作为主要的综合方法得到了深入研究[8-12]。但是对于四杆机构的综合问题，由于机构几何参数多，求解相对困难，为工程应用设计人员提供满足设计要求的轨迹综合求解的有效方法还是很少，因此，完善轨迹综合求解的理论方法需要在提取轨迹特征参数的同时，尽可能减少不影响连杆轨迹曲线特征参数的机构参数[10]。在四杆机构中，平面四杆机构应用最为广泛[13]。文中以减少初始设计参数量为目标，在传统平面四杆机构轨迹综合求解理论方法的基础上，提出基于轨迹特征圆，通过对轨迹特征圆参数的提取计算，确定满足设计要求的目标机构机架安装位置参数，实现平面四杆机构连杆轨迹曲线的标准化,其过程如图1所示。

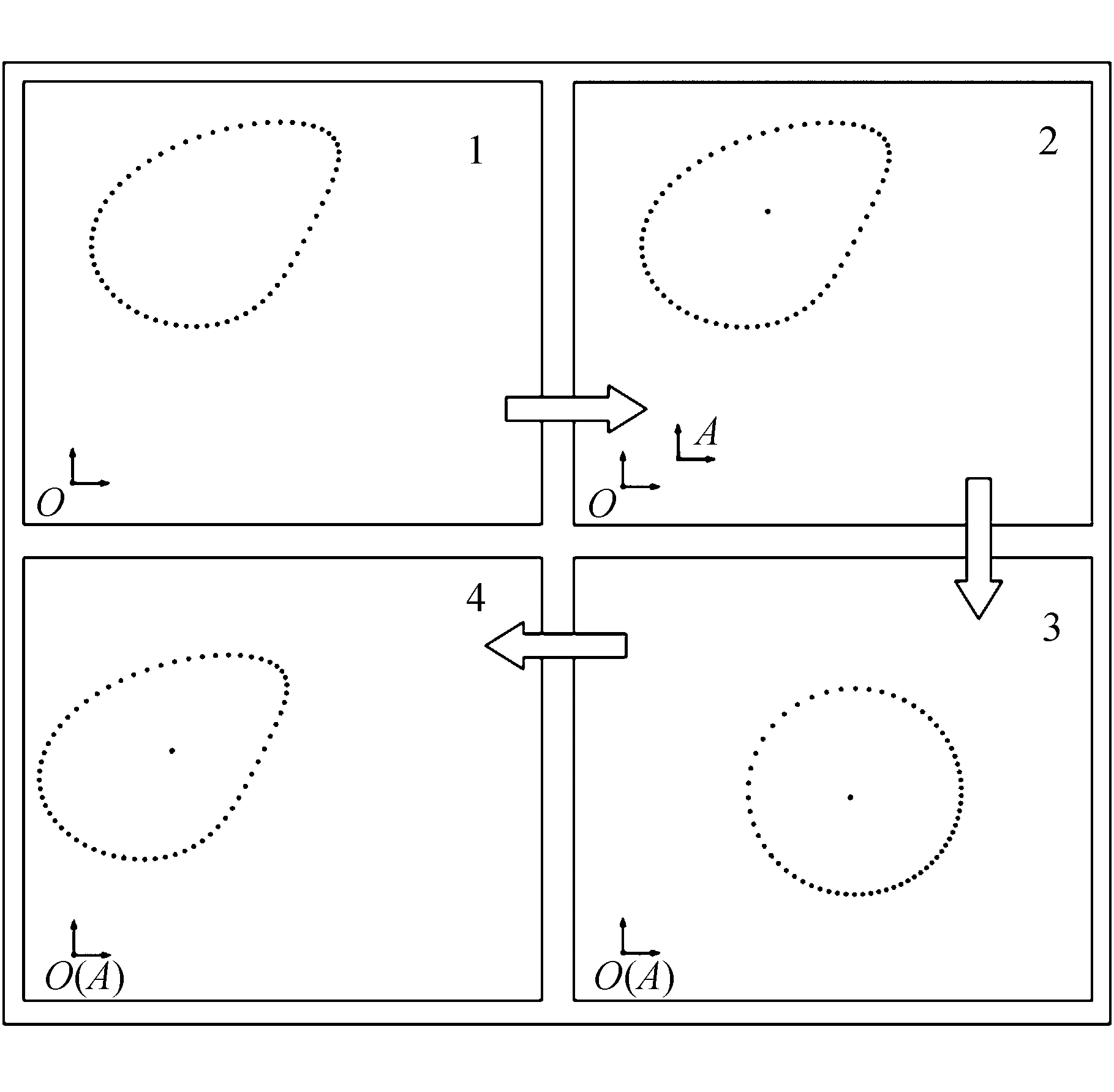
图1 平面四杆机构轨迹标准化处理

1 平面四杆机构连杆轨迹曲线的数学模型

标准安装位置的平面四杆机构如图2所示。

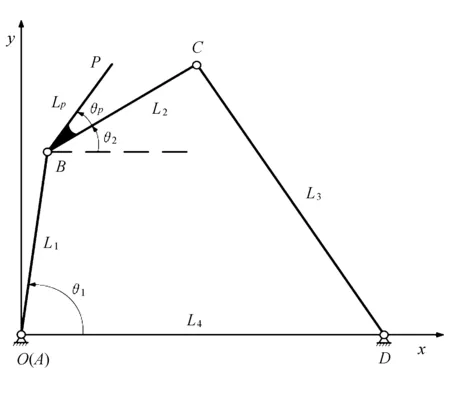
图2 标准安装位置平面四杆机构

机架AD与x轴重合，AB为输入构件，BC为连杆，CD为输出构件，AD为机架。机构中各杆AB、BC、CD、AD长度分别为L1、L2、L3、L4。θ1为输入构件转角，θ2为机构连杆转角。位置参数Lp、θp表示连杆上一点P，BP的长度为Lp，且与BC的夹角为θp,θp为BP与连杆BC之间的夹角。根据平面四杆机构杆件角度关系，连杆上P点连杆轨迹在坐标系Oxy表示为：

xp=L1cosθ1+Lpcos(θp+θ2),

(1)

yp=L1sinθ1+Lpsin(θp+θ2)。

(2)

定义Oxy坐标系为复平面坐标系，实轴x轴，虚轴y轴，则连杆P点坐标系位置可表示为

Fp=xp+iyp,

(3)

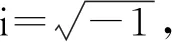
Fp=L1cosθ1+Lpcos(θp+θ2)+

i[L1sinθ1+Lpsin(θp+θ2)]，

(4)

将cosθ+isinθ=eiθ代入式(4)，则

Fp=L1eiθ1+Lpei(θp+θ2),

(5)

对连杆P点轨迹间隔Δθ进行离散采样2j(j∈N*)个点(Δθ=2π/(2j-1))，采样点的坐标为

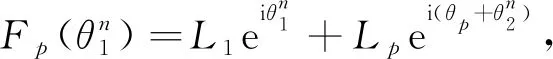
(6)

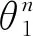
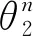
将采样点对应旋转相应的输入角得

(7)

指定标准安装位置的平面四杆机构，机构L1=50 mm、L2=120 mm、L3=86 mm、L4=140 mm、Lp=150 mm、θp=60°,输入构件转角θ1∈[30°,390°]。对指定平面四杆机构的连杆轨迹曲线进行离散采样64个点，采样点旋转对应的输入角，旋转后的采样点位置落在轨迹特征圆上。标准安装位置平面四杆机构的轨迹特征圆曲线如图3所示。

图3 标准安装位置平面四杆机构的轨迹特征圆曲线

轨迹特征圆的半径长度为Lp=150 mm，圆心坐标为Oc(50,0),L1=50 mm。基于这一发现，满足设计要求的目标机构安装位置可以通过连杆轨迹特征圆近似确定。

2 平面四杆机构的轨迹曲线标准化处理

对于一个标准安装位置的平面四杆机构，通过上述处理方法对连杆轨迹进行采样，可以计算出轨迹特征圆参数。在实际平面四杆机构的应用问题中，机构往往是一般安装位置。连杆轨迹曲线是由10个尺寸类型参数来描述,如图4所示。

图4 一般安装位置平面四杆机构

除了上面描述标准安装位置的7个尺寸类型参数外，还有3个安装位置参数：LA、θA和θ0。LA和θA是机架A点在坐标系中的平移参数，机架A的坐标(xA,yA)可以表示为(LAcosθA,LAsinθA)；θ0是机架在坐标系中的安装角度。因此，连杆上P点在复平面坐标系Oxy的轨迹曲线可以表示为

Fp=LAeiθA+L1ei(θ1+θ0)+Lpei(θp+θ0+θ2)。

(8)

对连杆P点轨迹进行离散采样2j个点并进行预处理，即每个采样点减去安装位置平移量LAeiθA，旋转对应的输入角得

(9)

根据式(9)，生成的点位于一个轨迹特征圆上，圆的半径长度为Lp，圆心坐标为(L1cosθ0,L1sinθ0)，相位角为(θp+θ0+θ2n-θ1n)。因此对目标轨迹离散采样，并对采样点进行预处理，找到一个轨迹特征圆就可以确定目标机构的安装位置。换一种说法，如果确定机架A点安装位置，将目标轨迹的采样点进行预处理，生成的这组点最大接近一个圆，便是可以满足设计要求的目标机构的连杆轨迹特征圆，机架A点位置即是目标机构的安装位置。

通过上述分析，文中重点需要确定A点坐标(xA,yA)，将目标轨迹的采样点进行预处理，得到的一组点与一个圆相匹配。如果只有三个点，在它们上面就会有一个圆；如果超过三个点，就不可能画出一个与这三个点完美匹配的圆，需要一个近似值。同样，假如采样点只有三个点，在预处理后会在一个圆上。但是三个点并不能表示目标连杆轨迹曲线的变化，因此采样点需要一组点，对这组点进行预处理后，需要近似在一个圆曲线上。针对这一思路，提出一种对特征圆接近程度的误差函数作为目标函数进行优化,确定目标轨迹特征圆参数和目标机构安装位置的方法。

2.1 轨迹特征圆的拟合函数及圆心坐标计算方法

(10)

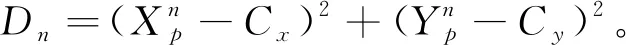
(11)

根据式(11)计算各个点的平均距离平方(定义为目标轨迹特征圆的半径)为

(12)

通过式(11)和式(12)可得各个点的特征圆接近程度的误差和函数δ为

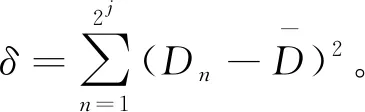
(13)

当目标轨迹采样点预处理后都在一条圆曲线上,且(Cx,Cy)是这条圆曲线的中心情况下，δ的函数值为零。因此可以用δ定量地判断目标轨迹采样点预处理后与目标轨迹特征圆曲线的接近程度，δ的函数值越小，目标轨迹特征圆越满足设计要求。

上述目标轨迹特征圆的圆心坐标(Cx,Cy)是设定的未知变量，式(13)是关于Cx和Cy的双变量函数，目标轨迹采样点进行预处理后的点在文中是给定的，因此当这组给定点和最优点(Cx,Cy)代入式(13)计算出δ最小值时，满足δ函数分别对Cx和Cy求一阶导数为零。因此，对式(12)进行展开整理为：

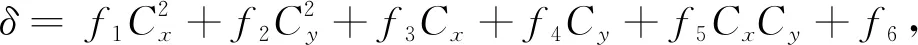
(14)

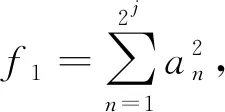
(15)

(16)

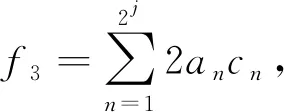
(17)

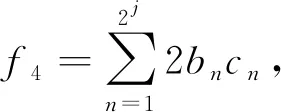
(18)

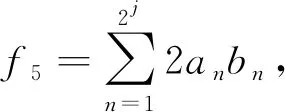
(19)

(20)

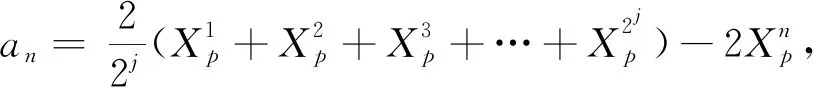
(21)

(22)

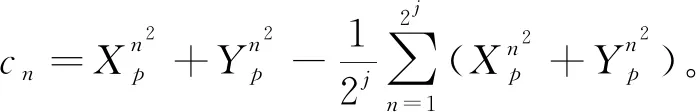
(23)

将式(14)分别对Cx和Cy求导：

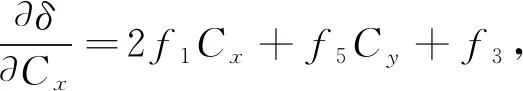
(24)

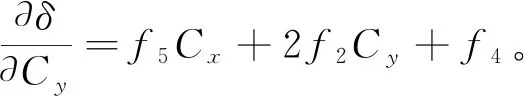
(25)

通过令式(24)、式(25)等于零确定δ最小值的方式求解Cx和Cy：

(26)

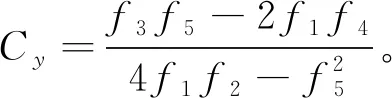
(27)

由式(26)和式(27)可知，目标轨迹采样点预处理后，可以直接计算出δ最小时的最优目标轨迹特征圆中心点(Cx,Cy)。这里需要进一步指出，当δ函数是二元变量函数，满足它的变量一阶导数为零的情况可能出现在最小值、最大值和鞍点位置。因此，应当验证δ函数取最小值时的必要条件[7]：

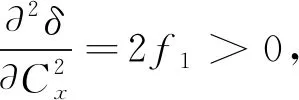
(28)

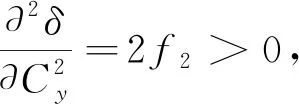
(29)

(30)

根据式(15)和式(16)可以得出不等式(28)、(29)条件成立。而不等式(30)可以通过柯西-施瓦茨不等式证实同样成立。因此，上述计算目标轨迹特征圆的圆心坐标方法是成立的。

2.2 目标函数分析

对于平面四杆机构的连杆轨迹生成综合问题，将目标轨迹采样点预处理后特征圆接近程度的误差函数δ作为优化目标函数。根据上述可知目标函数有安装位置xA、yA两个优化变量，这两个变量组成候选解，表示为向量X

X=[xA,yA]。

(31)

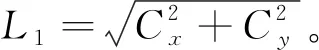
(32)

通过对目标函数优化可以得到机架安装位置xA、yA、连杆P点位置Lp杆长和输入构件L1杆长4个机构尺寸类型参数，实现综合求解的参数减少。

2.3 目标机构安装位置的优化方法

根据上述分析，目标函数在寻找最优两个变量xA、yA时，与传统的四杆机构参数优化方法相比，不需要考虑输入曲柄传动和Grashof′s判断等设计约束，避免在优化过程中xA、yA可行域的非光滑。

文中采用粒子群算法进行目标机构安装位置优化。粒子群优化算法最初是由Kennedy J等[14]介绍的，算法是基于蜜蜂、黄蜂、蚂蚁、白蚁、鱼、鸟的社会行为和动态运动，是一种全局优化算法，其中表示搜索变量集的粒子在目标函数变量空间中移动，定义第j个粒子的最优位置称为Pbest，每一次迭代的群的最优位置称为Gbest。每次优化算法迭代后，采用粒子更新方法计算每个粒子的新速度，

Vj(i)=ωVj(i)+c1rand(Pbest-Xj(i))+

c2rand(Gbest-Xj(i)),

(33)

式中：Vj(i)----第j个粒子在i次迭代中的移动速度；

Xj(i)----粒子当前的位置；

ω----惯性常数；

c1----加速常数，每个粒子的个体学习因子；

c2----加速常数，每个粒子的社会学习因子；

rand----0～1的随机数。

利用速度变化确定目标函数变量空间中提出的粒子更新位置

Xj(i)=Xj(i)+Vj(i)。

(34)

使用全局粒子群优化算法的优点是不需要粒子变换或惩罚函数。为了更好地理解对安装位置的优化方法，文中给出优化方法流程，如图5所示。

图5 目标机构安装位置优化方法流程

3 验证算例

为了检验所提优化方法的正确性，给定有时标的20个点为目标轨迹的采样点进行优化，见表1[15]。

表1 目标给定点及对应时标输入角θ1

在初始粒子数jmax=200和迭代次数imax=100的条件下对该问题进行优化，两个优化变量xA,yA∈[-50,50]，优化输出的最优解X=[5.696 9,15.210 3]，误差δ函数值为0.002 1。轨迹特征圆的半径Lp=163.471,圆心(Cx,Cy)坐标为(27.837 8,-0.00 82)。优化收敛过程如图6所示。

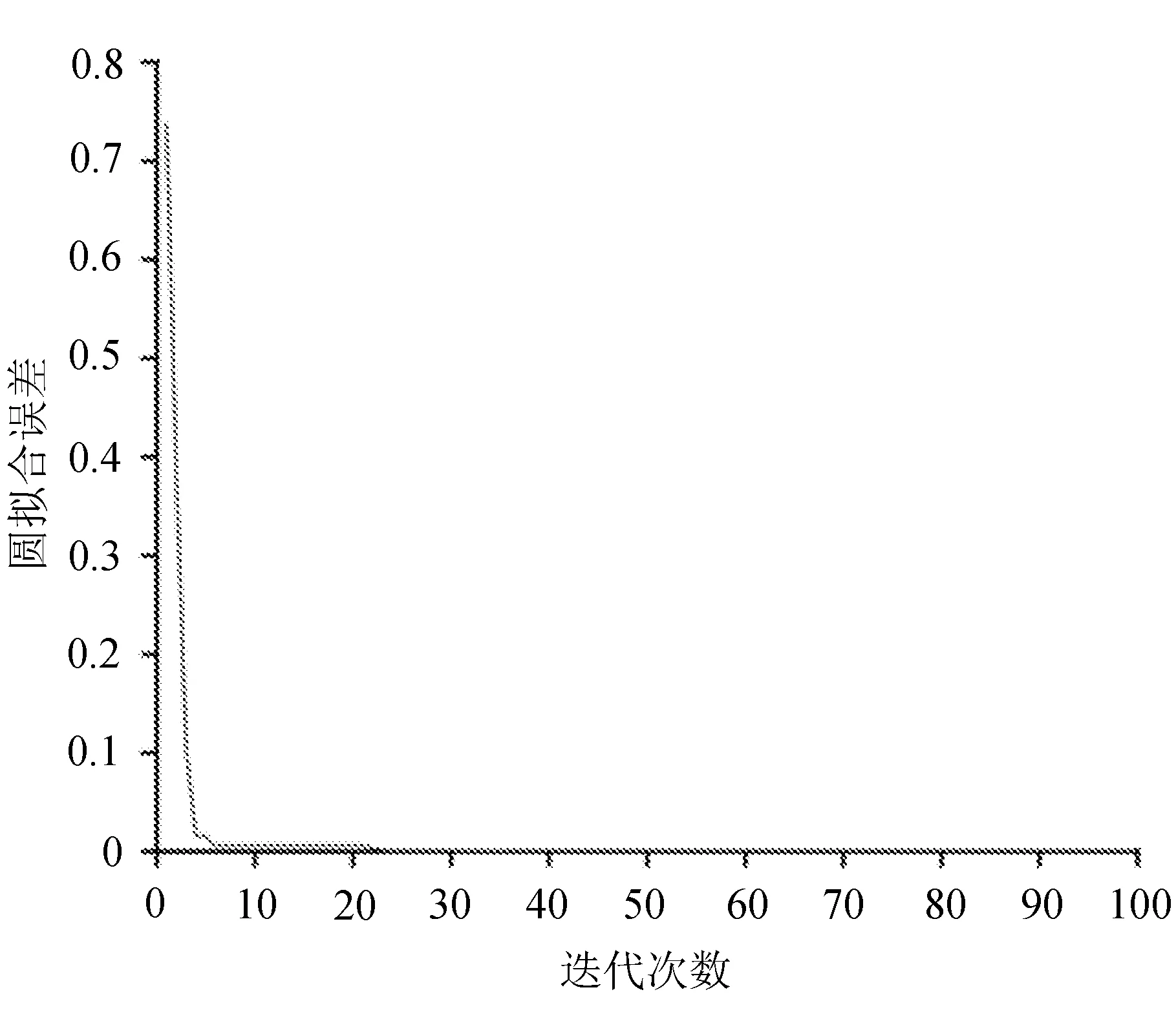
图6 优化收敛过程

根据优化结果，对给定点进行预处理后与轨迹特征圆的拟合如图7所示。

图7 给定点预处理后与轨迹特征圆的拟合图

图中圆点为给定点进行预处理后的点，实线为最优安装位置对应的轨迹特征圆，

4 结 语

针对全参数平面四杆机构连杆轨迹综合求解问题，通过对轨迹特征圆的发现及圆参数提取，将目标轨迹进行标准化处理，确定目标机构的安装位置。通过算例验证，在对轨迹特征圆接近误差函数进行粒子群算法优化的标准化过程中，可以快速收敛到全局最优解，得到目标机构机架安装位置、输入构件的杆长和连杆位置杆长参数，使得综合求解参数从10维变为6维，平面四杆机构连杆轨迹可以分步综合，降低了综合求解难度，为其它全参数四杆机构的轨迹综合求解提供了思路。