用介电质超表面产生准艾里光束

吴双宝，文 静

（上海理工大学 光电信息与计算机工程学院，上海 200093）

引 言

艾里波包的概念最早是在1979年由Berry等在量子理论的背景下通过求解薛定谔方程得出的[1]。艾里光束是由Siviloglou等[2]在2007年通过提出截趾因子把无限能量的艾里波包截趾成有限能量才得以第一次引入到光学中，并于同年得到了实验验证[3]。此后，艾里光束的产生方法和艾里光束的性质被广泛研究。目前艾里光束的产生方法主要有：利用空间光调制器（ SLM）加载立方相位模片再经过傅里叶变换得到[3-4]；利用光刻胶制作的连续相位板来调制高斯光束得到[5]；通过径向3/2相位编码在相位掩模对入射光束的不同位置改变不同衍射角来生成艾里光束[6]；在金属等表面薄膜上按照艾里函数振荡振幅分布和交替相位分布刻蚀出相应的光栅图案来产生艾里形式的表面等离激元[7-9]；利用二次非线性光子晶体[10]产生艾里光束等。同时，由于艾里光束的无衍射和自加速等特性，人们对艾里光束的传输性质[11-13]和应用[14-19]都做了大量的研究。对于利用液晶空间光调制器产生艾里光束的方法，SLM较大的体积及其所导致太过庞大的系统，因此不利于粒子操控的微纳应用。此外，还需要小心地调整高斯光束的束腰直径，以使其能和加载到SLM上的相位相匹配。对于表面等离子体激元法，通常产生的都是一维的艾里光束。

为了克服上述产生艾里光束的缺点，本文设计了一种全介电质几何相位型超表面[20-21]来生成艾里光束，亦称作准艾里光束。与传统的通过面形和厚度来实现光调制的光学元件或衍射光学元件相比，本文所设计的超表面器件具有超薄的结构，更利于与其他器件进行集成，同时还拥有更加灵活的相位调控能力等优点。为了说明所设计的超表面的有效性，还使用了有限时域差分（FDTD）算法进行了仿真。

1 介电质超表面产生艾里光束原理

1.1 介电质超表面结构

对于各向异性[22]的超表面，假设其主轴的局域坐标系由u和v构成，与笛卡尔坐标系的夹角为θ，如图1（a）所示。假定两个主轴方向的投射复振幅分别是tu和tv，几何相位的产生可以通过琼斯矩阵来描述，即

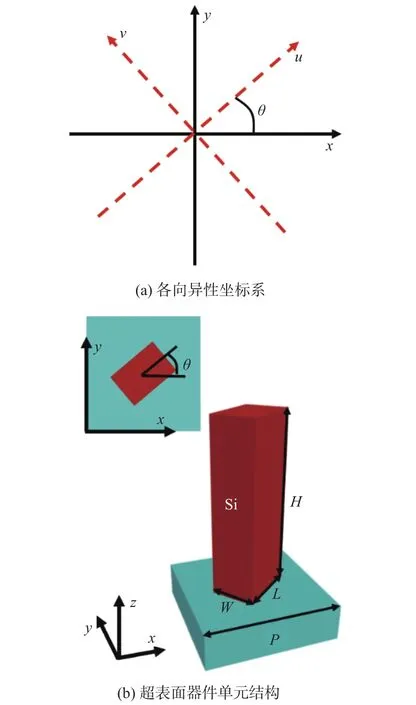
图1 硅纳米柱的几何尺寸与旋转角度Fig.1 The geometry and rotation angle of silicon nanopillars

当入射光束是左旋圆偏振光时，光束经过各向异性超表面后，输出的电场信息可表示为

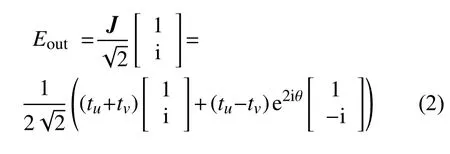
由式（2）可知，当左旋圆偏振入射光经过各向异性的超表面后，出射的电场含有原左旋圆偏振光的电磁波外，还含有复振幅为 (tu-tv)e2iθ的右旋圆偏振的电磁波，并且多了与夹角θ有关的附加相位。几何相位型超表面的单元结构对不同的偏振态具有各向异性，tu和tv是不相等的，这也就导致了偏振转化效率的差异。由此说明，为了能让器件高效地工作，需要使出射光中含有与入射光旋向相反的光能量尽可能的高。

超表面器件由如图1（b）所示的单元结构组成。在材料为SiO2的基底上分布有不同旋转角θ的纳米硅柱，图中周期P为290 nm，长L为190 nm，宽W为95 nm，高H为380 nm，单元结构的偏振转化效率为83%。当结构几何尺寸不变而改变旋转角θ时，器件可以产生0～2π的相位分布。对于左旋圆偏振入射光，器件的偏振转换效率由出射的右旋圆偏振光功率除以入射光的功率得到。在考虑实际器件加工工艺水平的基础上，通过有限时域差分（FDTD）算法来优化得到最终器件的长、宽、高、周期的数值，使其能够在设计的波长处高效率地工作。

1.2 艾里光束产生原理

二维有限能量的艾里光束在初始位置处可以表示为

式中：Ai为艾里函数；x0和y0都为横向缩放因子，通常情况下x0=y0；a为衰减因子。对初始位置处的光场分布进行傅里叶变换，可以得到其傅里叶频谱分布，即

式中： F 为傅里叶变换；kx和ky都为空间频率坐标；b为常数。可以看出，有限能量的艾里光束的傅里叶谱是一个由立方相位调制的高斯型分布。在得到频谱面的信息后，就可以利用透镜的傅里叶变换性质来产生艾里光束，产生艾里光束的原理如图2所示。在透镜的前焦面上放置一个被适当束腰的高斯光束照亮的具有立方相位分布的衍射屏，这时在透镜的后焦面上就可以得到艾里光束。但是这个方法使得光学傅里叶变换的系统长度达到了2f，不利于系统集成和小型化。同时该方法还需要调整高斯光束的束腰，使其和立方相位模片的大小相匹配。

图2 艾里光束产生原理Fig.2 Principle of generation of Airy beam

本文利用文献[23]中所用到的方法，即利用菲涅耳全息透镜来实现傅里叶变换。对菲涅耳全息透镜的相位信息进行编码并将其叠加到对应的立方相位中，由于编码是离散的，所以需要满足奈奎斯特采样定理，菲涅耳透镜的焦距[24]应该不小于NP2/λ （λ为波长，N为超表面器件横向的像素数，P为超表面单元周期长度）。

对于艾里光束的傅里叶谱，其复振幅函数由呈高斯分布的振幅和呈立方分布的相位组成，可以表示为

式中：A(kx,ky) 为高斯振幅；为立方相位。为了得到高斯振幅，通常会采用高斯光束作为入射光，而本文采用平面波作为入射光束，并利用Davis等[25]提出的纯相位的编码方式，将振幅的信息叠加到相位中。当振幅信息叠加到相位中，光束的复振幅函数可表示为

图3 利用超表面产生准艾里光束Fig.3 Using metasurface to generate quasi Airy beam

2 仿真和结果分析

利用FDTD算法仿真来对本文设计的能够生成艾里光束的全介质超表面器件进行验证。由于几何相位的偏振敏感特性[26]，仿真采用左旋圆偏振状态的平面波作为光源，光源波长是630 nm，缩放因子x0=y0= 0.3 μm，b= 0.03，起傅里叶变换作用的菲涅耳全息透镜的焦距是18 μm。由于光源是左旋圆偏振光，根据式（2）可知，出射光束会转换为与入射光相反旋向的光束。由于受偏振转换效率的限制，出射光中还会携带有原来的左旋圆偏振光的成分，我们将其视作噪声而将其过滤掉，以下仿真结果均为已过滤噪声后所得的结果。

以超表面平面作为z= 0平面，如图4为艾里光束在不同传播距离处的光场分布，分别记录了z= 20 μm、25 μm、30 μm、35 μm、40 μm 处的光场信息，所有的强度分布都是经归一化后的结果，所有横向白色标尺均为4 μm。其中图4（a）～（e）是将总相位（将振幅信息进行编码叠加到相位，再加上菲涅耳透镜相位得到的总相位）加载到超表面上后经FDTD仿真得到的结果；图4（f）～（j）是没有将艾里光束频谱的高斯分布振幅信息编码进总相位中，仅仅只有立方相位加上菲涅耳相位的编码，不包含振幅的信息，其他参数均与（a）～（e）相同。对比两种仿真结果可以发现，这种通过编码菲涅耳透镜到频谱相位中来进行傅里叶变换进而产生准艾里光束的方式，在缺乏振幅信息的情况下不会对准艾里光束的轨迹和光场分布产生明显影响。由此说明，对于这种产生艾里光束的方式，振幅信息不是必要的信息，于是可以简化流程，可以更方便地产生艾里光束。

图4 振幅相位同时调制和仅相位调制的超表面产生准艾里光束在不同平面处的光场分布Fig.4 The optical field distribution of quasi Airy beams in different planes produced by a metasurface with simultaneous amplitude and phase modulation and only phase modulation

从图4可以看出，随着传播距离的增加，艾里光束（亦称作准艾里光束）的主瓣和两翼的尺寸都会逐渐增大。这种逐渐扩散的原因是我们利用了菲涅耳全息透镜而非一般的球面透镜来进行傅里叶变换，这种方法缩短了傅里叶变换所需的2倍焦距的长度，但同时也带来了一个菲涅耳衍射问题。将式（5）乘上透镜的透射函数并以透镜位置作为初始平面，则在透镜后焦面处的复振幅分布可表示为

式（8）表明，在透镜的后焦面上，除了含有频谱面复振幅分布的傅里叶变换之外，还含有一个振幅和二次相位分布。我们知道，频谱面经傅里叶变换后的分布正是艾里光束的复振幅分布，而正是这个附加的二次方相位，使得我们所得到的光束并不是真正意义上的艾里光束，所以我们将其称之为准艾里光束。

这种方法除了会产生一个类似球差并使光斑放大的效果外，还会使艾里光束的主瓣轨迹发生改变。理论上，艾里光束的主瓣轨迹在y方向可以描述为而利用本文方法产生的准艾里光束的主瓣轨迹[4]为y=cz2/(z+f) （其中c是一个常数）。所以这种方法产生的准艾里光束不再是一个抛物线，如图5所示。

为了验证本文方法产生的准艾里光束的自修复性质，我们在前述准艾里光束主瓣的传播路径上，放置了一个边长为1 μm的硅方块作为障碍物阻碍光束的传播，并测试了z=20 μm、25 μm、30 μm、35 μm 处的光场分布，结果如图6所示。从图6可以看出，准艾里光束在被障碍物阻挡后，很快就恢复了原有的轮廓。

图5 超表面产生的准艾里光束和相同参数的艾里光束的轨迹对比Fig.5 Comparison of the trajectory of the quasi Airy beam generated by the metasurface and the Airy beam with the same parameters

图6 准艾里光束的自修复特性Fig.6 Self-healing characteristics of quasi Airy beam

3 结 论

傅里叶变换法是一种典型的产生艾里光束的方法，相较于传统的利用入射高斯光束获得振幅信息的方法，我们将振幅信息和相位信息同时编码并采用平面波作为入射光来产生艾里光束。本文使用全介电质超表面来产生艾里光束，利用FDTD算法验证了本文设计的全介电质超表面器件在波长630 nm处可以有效的工作。相较于传统的液晶空间光调制器（SLM）产生艾里光束方法，由于本文所采用的超表面具有亚波长的单元尺寸，可以有效解决液晶空间光调制器的单个像素尺寸较大而使相位梯度较小的限制，同时超表面器件作为一种超薄器件，比液晶空间光调制器更加有利于系统集成。研究发现，利用本文方法产生的准艾里光束其频谱的高斯振幅可以忽略，这方便了艾里光束的产生。由于本文所设计的超表面器件产生的并不是严格意义上的艾里光束，而是随传播距离的增加光束轮廓会不断放大的准艾里光束，因此下一步的研究方向是消除因编码菲涅耳透镜相位来做傅里叶变换引入的误差。