装药结构对深孔爆破粉矿产出率的影响研究①

2021-05-16李小元史秀志罗志华

矿冶工程 2021年2期

孔坤，李小元，史秀志，陈飞，喻智，罗志华

（1.中南大学资源与安全工程学院，湖南长沙410083；2.广西中金岭南矿业有限责任公司，广西武宣545900）

在矿山井下深孔爆破作业中，矿石的损失率是评估资源回收效率的一个重要指标。受限于铲装机械设备精度，过小块度的矿石往往无法有效铲装，进而成为矿石损失的一个重要原因。有研究表明，装药结构对粉矿产出量有重要影响［1］。合理的孔内装药结构能使爆破能量分布更均匀，粉矿比例降低，从而保证矿山经济效益和生产流程平稳。

运用数值模拟软件对爆破结果进行模拟分析具有低成本、高效率的特点，故应用广泛［2－5］。以往多数研究重点关注爆破后的整体破碎效果，而较少关注装药结构对粉矿具体产出量的影响。本文在分析南方某矿山现有大直径深孔装药结构的基础上，提出了6种深孔装药结构，运用ANSYS／LS-DYNA软件从失效比例和块度分布两方面进行对比分析，最终得到粉矿产出控制效果最好的装药结构，并于该矿山开展了现场实践。ANSYS／LS-DYNA软件作为一种显式动力分析软件，因具备众多的材料动态模型和接触类型，在高速、高压且瞬时的爆破研究领域应用较广。其中最常用的分析计算方法有Lagrang算法、Euler算法和ALE算法，前两种算法在处理爆炸大变形问题上会因自身限制而导致网格严重畸变，而后者却不会出现这种情况［6］。因此，本文采用ALE算法进行模拟研究。

1 工程概况

南方某矿山采用大直径深孔爆破的采矿方法，采矿工艺如图1所示［7］。在采场上部凿岩硐室内采用人工掏槽或天井掏槽的方式布置掏槽区，随后以掏槽区为中心，沿采场走向布置列距2～2.2 m、排距1.8～2.2 m的4排垂直向下炮孔，用于后期侧向崩矿。采场爆破顺序为：掏槽区首先起爆，在经过多次爆破形成足够补偿空间后，根据碎胀系数对采场剩余部分进行分次侧崩爆破，直至采场全部回收。

图1 采矿工艺示意

该工艺方法简单、采切量小且安全高效，为矿山带来了巨大的经济效益。但在长期生产实践中发现后期侧向崩矿时因每次崩矿量大、药量多和自由面多等因素，若采用与掏槽孔相同的装药结构会导致单耗过大、粉矿率过高，不利于后期回收，易造成矿石损失。因此，合理选择侧向崩矿时的装药结构，控制粉矿产出，对矿山具有很重要的现实意义。

2 模型建立

根据矿山实际情况，炮孔模型直径110 mm，炸药模型直径90 mm，长度700 mm。在孔径不变和大块率满足要求的基础上，利用每层药包数量和间隔距离的不同，选取了6种不同的间隔装药方式，每组模型的详细装药参数如表1所示。

表1 装药参数

每组模型厚度均为1 mm，炮孔左侧为4 m的待采区，右侧为2 m的开挖区。为防止边界对模型计算的影响，将上、下以及左侧边界均设置为无反射边界，右侧边界为自由面。为最大限度减少反射应力波对模拟结果的影响，特将孔内装药层数定为4层，主要研究中间两层药包的影响作用。图2为模型4示意图。

图2 模型4示意图

爆破模拟中应用到的材料模型有岩石、炸药、爆轰产物和孔内间隔空气，因此在模型计算前，需对所有材料进行本构模型和相应状态方程的建立，并确立方程中各参数的数值。

其中，为更加接近真实的岩石特性，选择在应变率效应、围压效应和岩体损伤演化效应方面具有突出特点和优势的HJC模型［8］，它与金属材料中应用广泛的Johnson-Cook材料模型相类似，等效屈服强度是压力、应变率及损伤的函数，损伤量则是塑性体应变、等效塑性应变和压力的函数［9］。

3 研究结果分析

3.1 失效比例分析

为了更好地研究岩体在爆破后的失效情况，在上述模型关键字文件中添加拉伸失效命令*MAT＿ADD＿EROSION。为最大程度避免反射应力波对模型的影响，当冲击波传递到最左侧边界时终止计算，得到6组模型最终失效图如图3所示。图中A、B、C所代表的区域即为本文的研究范围，A、C区域代表炸药所对应的爆破失效范围，B区域代表空气间隔所对应的爆破失效范围。

图3 各模型最终失效图

图中因失效而被删除的白色“裂纹”区域即为体积减少量，失效比例则是每个失效图中研究区域的体积减少量与该区域原有体积量的比值。分别对爆破失效后的A、B、C区域以及ABC整体区域进行失效比例计算，将3个小区域的失效比例与整体区域失效比例进行比较，若两者差别较大，则表示炸药能量在整体分布上不均匀，导致矿石块度大小各异；若两者差别较小，则表示在该种装药方式下炸药能量在整体上分布均匀，特别是空气间隔部分也得到了充分的爆破。

使用后处理软件分别对6个失效图内的研究区域进行体积计算，并计算各组模型的失效比例以及单个区域失效比例方差S1、单个区域和ABC整体区域之间差值的方差S2，效果见表2～3。由表2～3可看出，模型4的B区域和整体区域的失效比例分别为29.04%和34.95%，是所有分区失效比例和整体失效比中最小的，同时其方差S1和S2也是所有方差中最大的，说明在该种装药结构下岩石整体爆破效果较差，尤其空气间隔部位破碎不彻底，易出现大块，因此首先可排除模型4的装药方案。同时，表中模型3、5、6的方差S1和S2差值较大，侧面表明炸药能量在各个区域的分布并不均匀，炸药层能量多，空气层能量少，容易在炸药层产生粉矿。模型1和模型2的方差S1、S2相差较小，说明这两种装药结构能够将炸药能量最大程度地均匀分布到各个区域，可同时控制粉矿和大块矿。

表2 模型失效前后体积量

表3 方差计算结果

3.2 裂纹交错块度及粉矿

图3 中因失效而被删除的白色“裂纹”虽与实际爆破后的裂纹扩展有一定差异，但在总体上与爆破后裂纹扩展方面具有高度的相似性［10］。因此，本文利用这些“裂纹”交错所形成的块状区域来“代替”实际爆破块度是可行的。由于ANSYS软件没有考虑到爆破抛掷作用对矿石块度的影响，因此需要使用块度处理系统［11］对失效图进行系统识别和人工“打断”，使某些因抛掷碰撞而实际会分裂的大块体变得破碎，更加接近于实际爆破后的块度。以模型2为例，处理前后的块度图如图4所示。随后利用系统的统计分析功能对得到的高清分析图进行块度尺寸分布统计，并将6组模型的尺寸分布数据导出，绘制成如图5所示的块度尺寸累计分布曲线图。

图4 模型2块度分析图

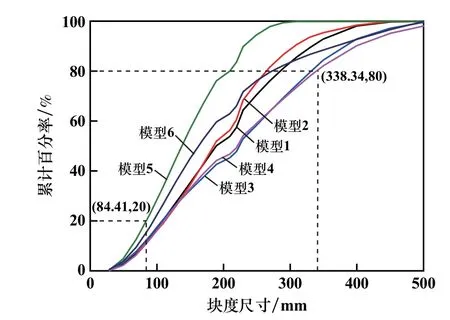
图5 块度尺寸累积分布曲线

现对图5中曲线进行数据分析，分别过20%、50%和80%做X轴平行线，并统计每组模型的最大尺寸Xmax，结果见表4。

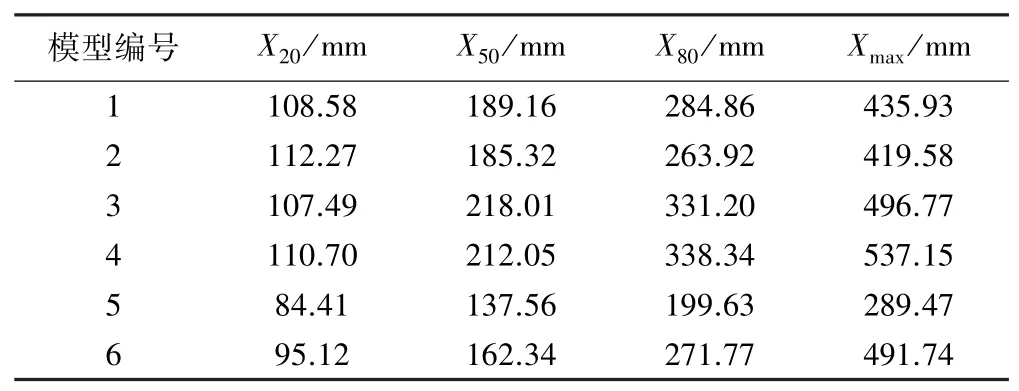
表4 块度尺寸统计表

从表4可以看出，模型5的X20和Xmax数值仅为84.41 mm和289.47 mm，是所有数值中最小的；模型6的X20过小而Xmax偏大；同时，模型3、4的Xmax数值也过大。说明在模型5的装药结构下会产生过多粉矿；模型6的矿石块度多集中在小块度和大块度上，整体块度均匀性差；而在模型3、4的装药结构下却有可能产生大块矿。

现根据文献［12］提出的“两边加法则”对模型1和模型2进行深度对比。其具体操作为：对表4中得到的12组X20和X80数据进行比较，将最小的X20定为粉矿上界，最大的X80定为大块下界（也可如图5中所作直线获取），得到粉矿上界为84.41 mm，大块下界为338.34 mm。现将这两个指标反推至图5中，可得到模型1、2的特征尺寸块度比例如表5所示。

表5 特征尺寸块度比例表

观察表5可知，模型2的粉矿比例和大块比例相比模型1都较小，表明该种装药结构下所达到的控制粉矿和大块矿的效果最好，因此认定装药结构2（1条炸药-1.0 m间隔-1条炸药）为最优的装药结构。

4 工程应用效果

实际生产中矿山将粉矿上界定为3 cm，即块度小于3 cm的矿石即可认定为无法回收。现进行矿山现场试验，该采场已经过3次拉槽，后续回采均为侧向崩矿。图6（a）为应用前爆破效果，采用模型5的装药结构，可看出爆破后粉矿产量过多且有大块；图6（b）为应用模型2的装药结构后的爆破效果，采场矿块块度均匀，粉矿产量少。后期铲矿过程中也并未发现大块，即不会出现二次处理大块的工作，采场资源回收率相比以往更高。由此说明，本文研究得到的装药结构能够很好地满足矿山生产需求，基本解决了矿山粉矿率高这一问题。图中参考物为矿泉水瓶（瓶盖直径3 cm，瓶底直径5.5 cm，高18 cm）。