深海潜浮式提升舱的结构设计及水力学计算①

黎 宙

（长沙矿冶研究院有限责任公司 深海矿产资源开发利用技术国家重点实验室，湖南 长沙410012）

在深海采矿系统中，水下输送是一个十分重要的环节。目前，常用的水下输送方式包括连续输送和非连续输送两种类型［1］，其中连续输送主要是指矿物通过管道直接从采矿车输送至水面母船上，一般有水力、气力提升等；非连续输送则将矿物置于储料仓中，通过有缆或者无缆形式输送至水面［2］。连续输送效率高，但布放和回收复杂，受海况条件影响较大，且几千米长的管道对水面母船提出了很高的要求。非连续输送则对海况的适应性高，布放和回收操作简单，且可通过增加多个运输舱的形式提高运输效率。

本文以商业开采为背景，基于非连续输送的思想，提出了一种无人无缆式的潜浮式提升舱，通过对输送系统功能分析，提出了一种单运输主体＋多附体的结构，并对提升舱水平和竖直运动状态下的流体力学性能进行了仿真分析。

1 总体方案设计

1.1 功能需求分析

潜浮式提升舱作为一种从深海水下作业平台至水面母船的矿物运输工具，其主要性能如图1所示。

图1 潜浮式提升舱系统功能构成简图

1.2 总体结构设计

根据潜浮式提升舱的功能需求和相关分析，得到其总体输运方法如图2所示。

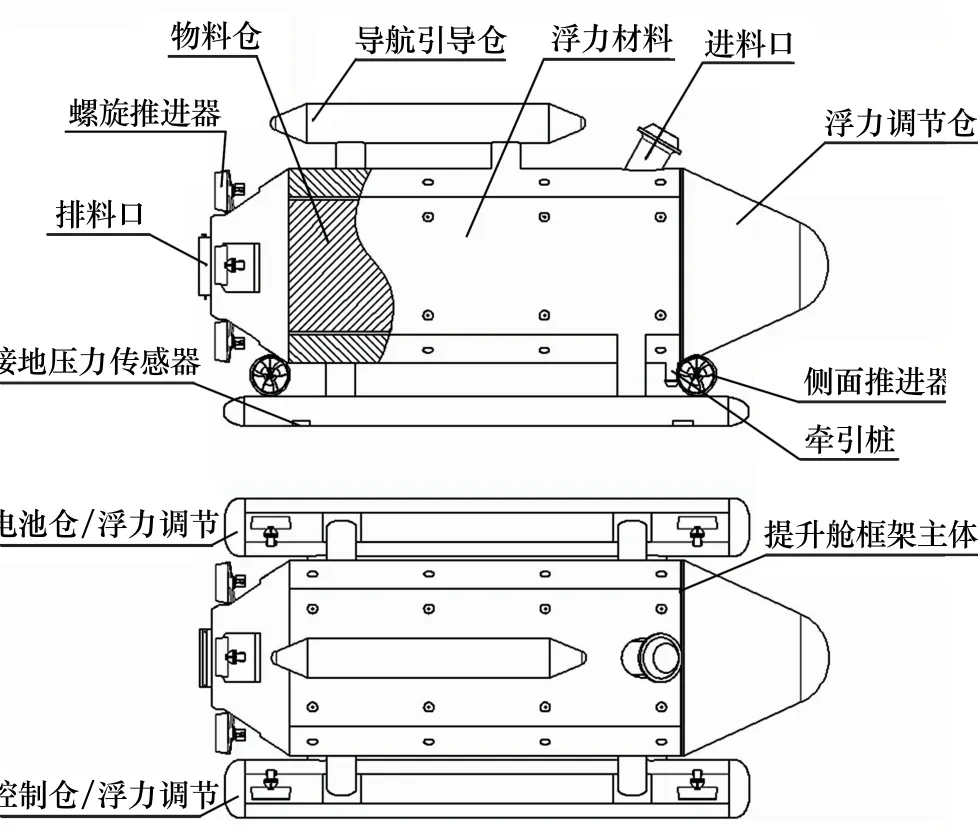
图2 潜浮式提升舱总体设计

潜浮式提升仓整体外形为流线型，尽量减小其在运动过程中所受的水阻力；前端具有流线形整流罩，具有调节浮力的功能；料仓为透水结构设计，分别与进料口和排料口相连，可避免受海底高压环境影响；电池仓和控制仓通过连接构件分别连接于主体侧下方，均具有调节浮力的功能，同时为主体提供支撑，其上布有接地压力传感器，用于感知提升舱的接地和物料装载状态；主体上方布置有导航引导仓，为提升舱水下的运动和水下对接提供指引；提升舱尾部均布有4个螺旋推进器，为物料向海面运输提供动力，侧面推进器主要用于布放回收和水下进料口对接时姿态的调整［3－4］。

1.3 作业模式

潜浮式提升舱的功能是由水下作业平台至水面母船之间的物料运输，如图3所示，其作业过程可分为如下4个阶段：甲板布放，水下运输，物料装载和甲板回收。其中水下运输包括提升舱在甲板布放后由海面到水下平台的运动过程以及提升舱装载物料完成后返回水面的过程。水下运输过程中，提升舱保持竖直向上的运输姿态，有利于减小其所受的水阻力。在海底和海面，基于布放、回收以及水下对接的要求，提升舱还需要有水平运动的要求。

图3 潜浮式提升舱作业模式

2 水力学计算

相对于其他水下载人或者观测型潜水器，潜浮式提升舱更侧重于承载能力和运动速度的功能，而对于其水下作业和操作性能要求相对较低，故综合考虑潜浮式提升舱在水中的力学行为关系到提升舱在水中的运动阻力、运动过程中的稳定性、运动控制的策略选择和控制算法的实现，有助于实现提升舱的最大运输效率。

潜浮式提升舱在水下工作时面临着恶劣的海底环境、复杂的海底地形地貌和激烈的深海海流，需要完成诸如水下平台对接、原地回转等灵活操纵运动，这都要求潜浮器具有良好的操纵性能和控制能力。从水动力角度看其主要特点是：①深海海底条件复杂，海流和海底地形条件难以预测，出于安全性考虑，操纵运动和控制上需要更为准确的水动力支持；②不同于一般潜水器，潜浮式提升舱体积和质量较大，为提高输运效率，需保持一个稳定经济的航速，且不能太低，故提升舱总阻力中的黏性阻力和惯性阻力均需进行详细分析。

2.1 计算模型

在数值计算中，物体结构越复杂，体积越大，所需网格数量就越多，且网格质量难以保证；同时对计算机硬件要求也越大，所需计算时间也越久。因此，为了提高计算精度、提高网格划分质量、加快数值计算的速度，将结构复杂的提升舱进行简化建模，按照1∶1的比例于深海流场中进行数值模拟，通过对提升舱结构和功能进行分析后，将简化模型定义为如下3个部分：主体、连接附件和附体部分（见图4）。由于提升舱在水下进行物料运输时，其作业姿态为竖直向上或向下，且在深海中，海流速度很小，基本可忽略，故对此种情况不同运动速度下的水阻力进行数值分析［5］。

图4 提升舱计算模型

2.2 计算域的划分

由于提升舱为左右对称结构，为节省计算资源、提高计算速度和精度，采用1／2模型进行计算，所建立的提升舱计算域如图5所示，设定其长、宽、高分别为L、B和H，则计算模型到速度入口距离为2L，到压力出口距离为4L，到上下壁面距离为2H，到侧面壁面距离为2B，使流场能在此计算域内充分发展，以保证计算准确性。

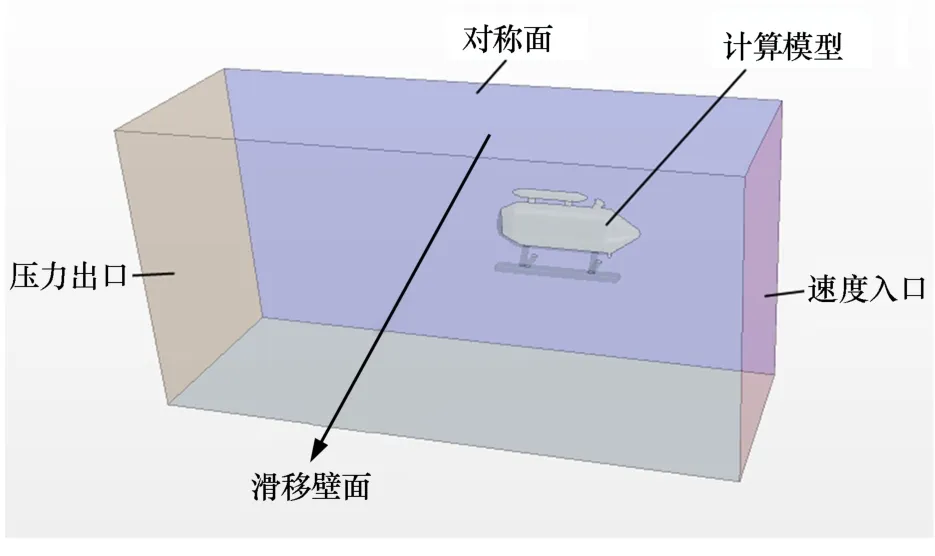
图5 提升舱计算域

2.3 网格划分

由于连接附件外表相对较复杂，存在曲面等特征，故采用非结构网格的划分方法。为获得精确的计算结果，模型外表面采用边界层网格结构，层数为8；计算域内采用自动六面体网格生成方式，生成的网格如图6所示，网格数量约为340万，网格质量最小为0.6，平均网格质量达到0.9以上。整个计算域采取多重网格加密的形式，在网格基本尺寸0.1 m条件下，分别按基本尺寸的50%、150%和250%作为3个加密区域的网格尺寸，使从模型表面到外边界层的网格由密到疏，实现网格大小逐步过渡，在达到良好的计算精度的同时节约计算资源、加快计算速度。同时在后处理过程中，模型附近密集的网格点分布有利于更好地观察其周边流场变化情况。

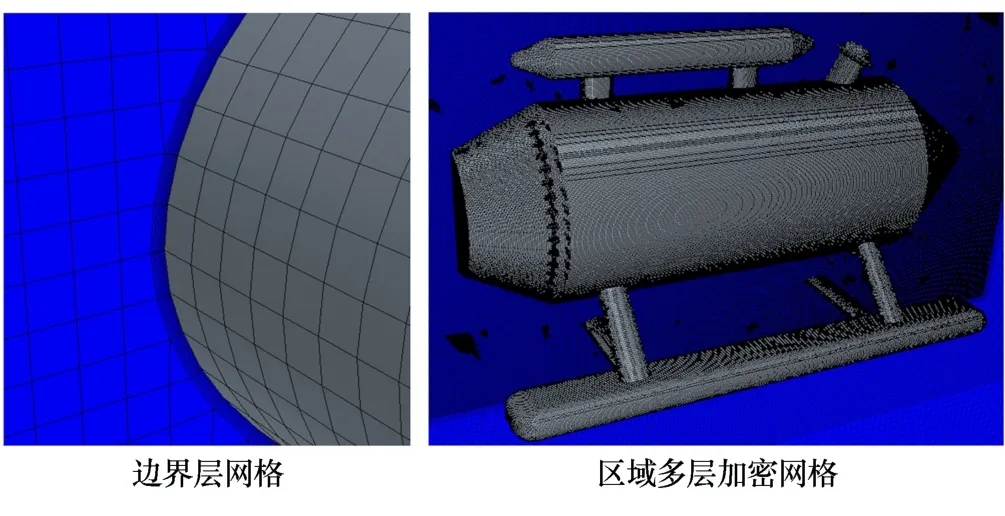
图6 网格划分

2.4 边界条件及计算模型选定

对计算域设置边界条件如下：

速度入口：模型向前2.5B，设定速度大小值为提升舱运动时的运行速度V，通过设定湍流强度与特征长度识别；

压力出口：模型尾部向后4B为压力出口，P＝1.01×105Pa；

壁面条件：模型外表面，无滑移；外场为滑移壁面；

对称面：垂直于对称面的速度分量Vn＝0，平行于对称面的速度分量的法向导数为零；

外场：距离模型表面高约2H，长为3L，速度为受扰动的主流区速度。

物理模型选用分离求解器，选用realizablek⁃ε湍流模型和雷诺平均湍流模型［6］。选取海水密度为1 010 kg／m3，动力黏度为1.3131×10－3Pa·s。

2.5 计算结果分析

提升舱在水中运动受海流速度、提升舱承载物料质量和浮力等因素影响，其速度在不同运动阶段不为一定值，故综合考虑提升舱整体作业情况，参考现有海洋勘探调查水下装备的运动速度，选择其速度计算范围为0.2～1.5 m／s。采用对称面的计算方法，边界入口速度分析分别设定为0.2、0.4、0.6、0.8、1.0、1.2、1.5 m／s，研究提升舱在不同速度下的水阻力变化。

图7 为提升舱运动速度1 m／s时对称面和底面的压力变化云图。可见提升舱前端压力呈梯度变化，压力随着与壁面距离减小而逐渐增大，最大可达555.9 Pa，物料接口处存在压差分离现象，提升舱的前方、本体部分及后方分别处在3个不同的压力环境下。

图7 提升舱对称面及底面压力变化云图

图8 为提升舱运动区域湍流黏度变化情况。可见在提升舱尾部存在很明显的湍流黏度变化，物料进口存在一定的湍流情况，电池仓和控制仓相对于主体湍流变化不明显。

图8 提升舱湍流黏度变化云图

图9 为流场域内提升舱周围的速度场分布。可见流体在经过主体后，产生明显的速度分离现象；料仓出口端存在明显的低速区域。

图9 提升舱周围速度流线图

图10 为提升舱主体阻力分布情况。可见提升舱阻力随速度增大而增大；在阻力组成中，以压差阻力为主，因为提升舱主体所占迎水面较大，黏性阻力在主体阻力中只占很小的一部分。

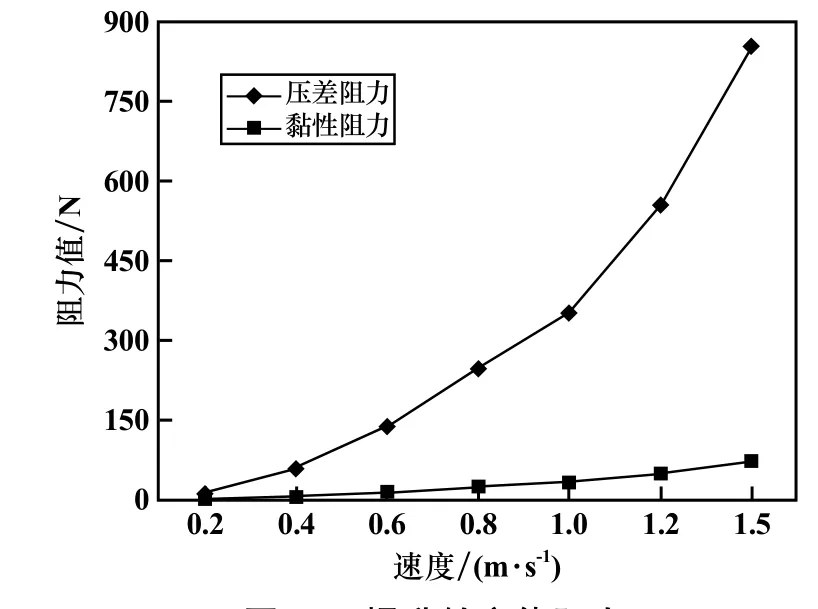
图10 提升舱主体阻力

图11 为附体在不同速度下的阻力变化情况。可见附体阻力组成中，黏性阻力和压差阻力所占比重基本一致。对附体的机体结构分析可知，附体主要包括电池仓、控制仓和声学仓，均为细长的圆和条状，所占迎水面积不大，但与流体接触面积较大，故会产生较大的黏性阻力，且随着运动速度增加，两者均逐渐增大。

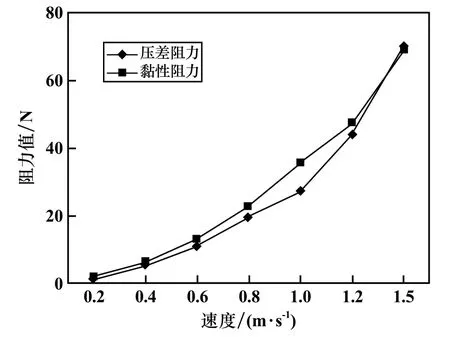
图11 提升舱附体阻力

连接附体的阻力主要指主体与附体之间连接部分结构的水阻力，如图12所示，连接附件的阻力以压差阻力为主，由于采用椭圆形的外形设计，在速度1.5 m／s时，压差阻力为192.78 N，黏性阻力为35.42 N。

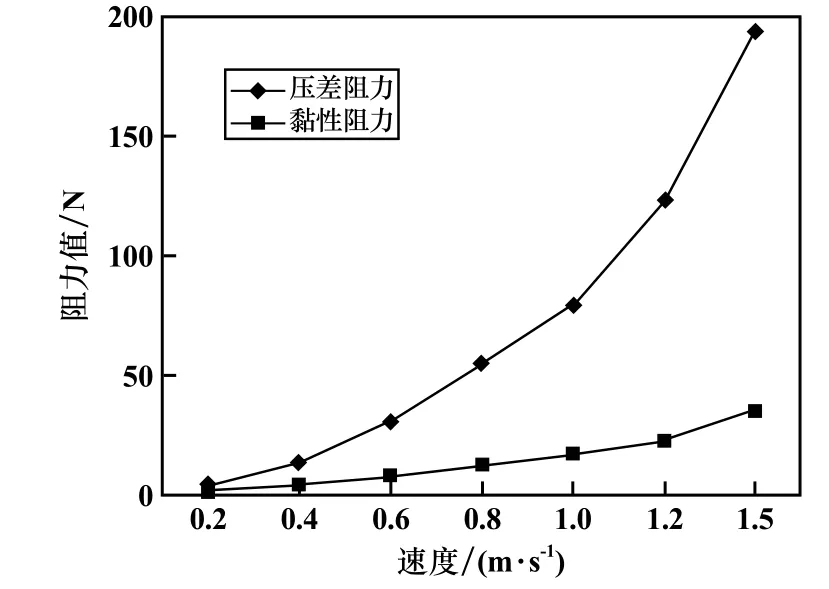
图12 提升舱连接附件阻力

提升舱的总阻力随速度的变化曲线如图13所示。分析可知，主体阻力是提升舱总阻力的主要来源，附体阻力所占比重最小，在速度1.5 m／s时，总阻力可达1 295.82 N。

图13 提升舱总阻力变化

3 布放姿态仿真分析

提升舱在从海面往下运动和往上运动接近海面时都不可避免地会受到海面海流的影响，故分析提升舱在运动时如何调整提升舱姿态使其受海流的影响最小，对于提升舱的控制和节约能源具有重要意义。图14为提升舱下放过程受海流影响示意图，图中所画来流方向为＋X方向，提升舱运动方向为＋Z方向，海流方向假定为与提升舱运动方向垂直，即处于XY平面内。

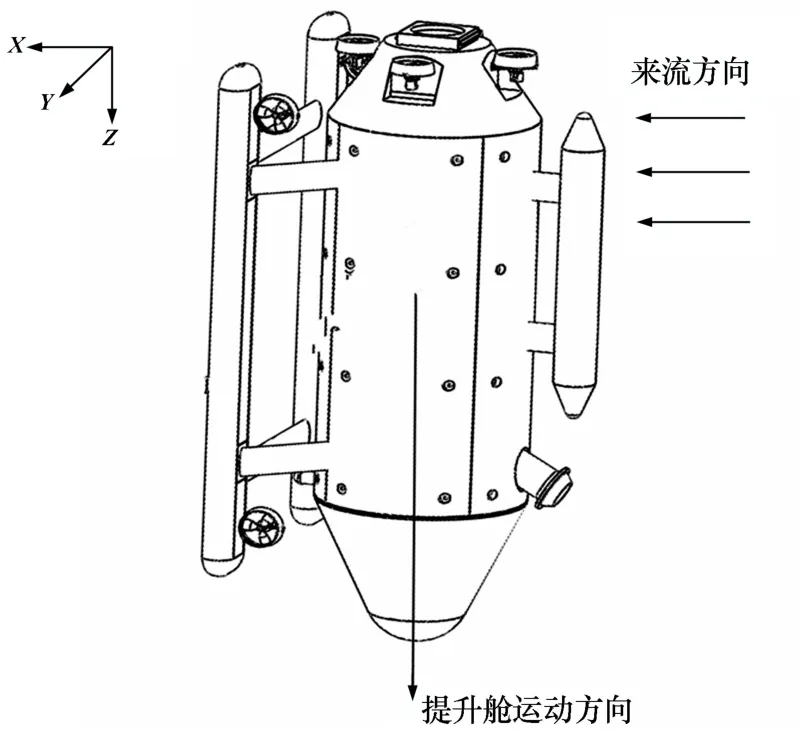
图14 提升舱下放时受海流影响示意图

采用完整的计算域进行计算，在海流速度设定为1 m／s的情况下，对以下几种工况进行分析：

工况1：来流方向为＋X，提升舱运动方向为＋Z；

工况2：来流方向为－X，提升舱运动方向为＋Z；

工况3：来流方向为＋Y，提升舱运动方向为＋Z；

工况4：来流方向与＋X，＋Y夹角为45°，提升舱运动方向为＋Z；

工况5：来流方向与＋X，－Y夹角为45°，提升舱运动方向为＋Z。

3.1 计算条件设置

流体域依然采用六面体网格，网格数量为304万，模型外表面采用边界层网格结构，层数为8；网格质量最小为0.7，平均网格质量达到0.9以上。整个计算域采取多重网格加密的形式，在网格基本尺寸0.5 m条件下，分别按基本尺寸的50%、20%和100%作为3个加密区域的网格尺寸，使从模型表面到外边界层的网格由密到疏，实现网格大小逐步过渡，在达到良好计算精度的同时节约计算资源，加快计算速度（见图15）。同时在后处理过程中，模型附近密集的网格点分布有利于更好地观察其周边流场的变化情况。

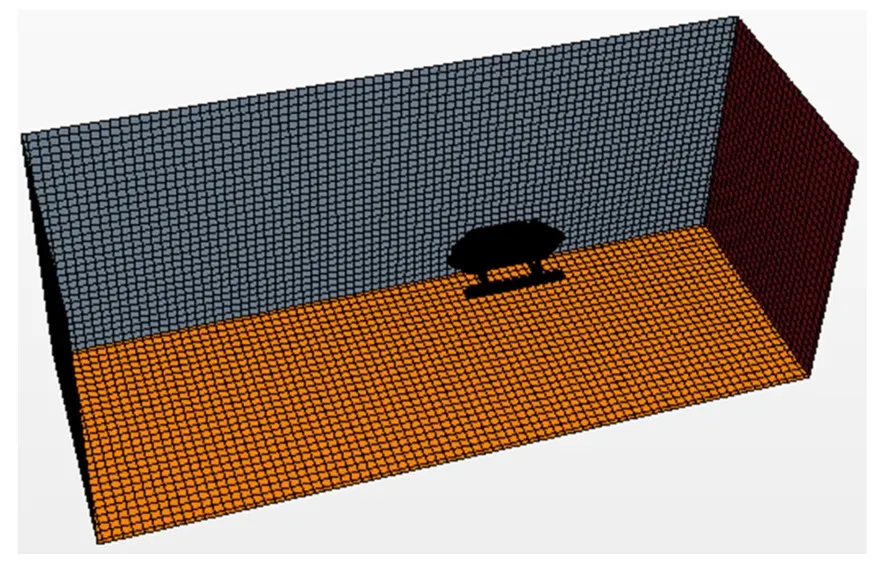
图15 计算域及网格划分

由于海底海流速度一般比较平稳，约为0～3 cm／s，且随着水深增加，海流速度逐渐变小。所以分别模拟计算连接附件在0.2、0.4、0.6、0.8、1.0、1.2和1.5 m／s下的运动情况，通过数值计算得出所受的水阻力大小，并对计算域内流场及模型表面各部分的压力分布情况进行分析。

3.2 计算结果对比分析

分别对以上5种工况进行流体计算分析，结果如表1所示。

根据表1中的提升舱表面流线及压强分布，结合所得的阻力数据可以看出，工况1和工况2条件下，提升舱主要阻力为X方向，工况1阻力相对较小；工况3、4和5条件下，X方向和Y方向均受到较大水阻力，不利于提升竖直方向运动和姿态的控制。因此，从提升舱便于控制和阻力最小的原则来看，工况1更有利于提升舱的水下运动。故建议在提升舱下放和回收过程中，调整提升舱的姿态以声学仓的方向迎流，更有利于矿物的运输。

表1 不同布放姿态仿真分析

3.3 工况1条件下不同速度阻力分析

在工况1条件下对不同海流速度作用下的水阻力进行分析。根据资料统计，大洋表面的流速一般为1～2节，约为0～1 m／s［7］，故分别在边界条件速度入口设置中设置X方向流速为0.2、0.4、0.6、0.8和1.2 m／s，Z方向速度保持为1 m／s，进行数值计算，结果如表2所示。分析表2数据可知，随着海流速度增大，提升舱X方向受力显著增大，呈正相关关系；Y方向由于提升舱结构的对称性，两边流场相似，故计算阻力较小；Z方向由于提升舱的运动速度为恒定值，受力较为稳定，在600 N左右波动。因此，在此种工况下，受海流影响时，应着重考虑X方向的受力，以达到稳定控制提升舱。

表2 不同海流速度下提升舱水阻力

4 结 论

1）针对深海采矿提升系统中难以应对恶劣海况的问题，提出了一种非连续输运模式——潜浮式提升舱，根据其功能需求，综合利用浮力调节、导航定位控制和水下接口技术等，对潜浮式提升舱进行了结构设计。

2）通过流体力学仿真软件对提升仓在水平运动和竖直运动的水力学进行了分析，计算结果表明，提升舱水平运动时，随运动速度增加，水阻力以压差阻力为主，黏附阻力相对较小。通过对提升舱不同迎流方向的计算表明，以声学仓正面迎流时，所受的流体阻力相对较小，且主要表现在X方向。在此工况下分别对不同海流速度下的阻力情况进行了分析，结果表明，随着运动速度增加，X方向阻力变化明显增大，Y和Z方向受力情况变化较小。