基于分数阶偏微分的井下移动设备在线检测数据融合算法∗

左延红程 桦程堂春

(1.安徽建筑大学 机电工程学院，安徽 合肥230601；2.安徽理工大学 土木建筑学院，安徽 淮南232001；3.国投新集能源股份有限公司煤制气项目部，安徽 淮南232001)

井下移动设备已广泛应用于我国地下工程建设和矿产资源开采作业领域之中，为了实现对井下移动设备的自动化管理，近年来，多数专家学者致力于物联网技术在井下移动设备信息监测与管理之中的应用研究，如文献[1]将物联网技术应用于井下移动变压器故障的分析与研究之中，文献[2]应用物联网技术开发煤矿安全生产监控平台，文献[3]应用物联网技术建设煤矿井下机电设备的检测管理平台。 以上研究成果均实现了应用无线传感网络技术对井下移动生产设备监测信息的实时获取功能，但这些研究成果至今未能在井下生产实践中得到推广与应用，究其主要原因在于:因井下移动设备在工作中位置处于随机变化状态，而井下工作环境恶劣，应用无线传感网络技术实时采集移动采煤设备监测信息时，监测信息的检测数据不仅要受到检测设备性能，还要受到设备工作环境和无线传输中信号干扰等诸多因素的影响，致使井下移动设备各类信息的检测数据存在较大的检测误差，直接影响着设备运行的安全性和生产管理系统工作的可靠性。

近年来，一些专家学者尝试将数据融合算法应用于井下生产信息检测系统的数据处理领域，并取得了一定的研究成果。 如王毅然为了准确判断煤矿工作面粉尘的分布状态，将D-S 证据理论和RS 理论两种算法综合应用于煤矿粉尘检测数据的融合处理中[4]；智宁、毛善君等应用一种基于深度融合网络的清晰化复原算法，解决当前煤矿尘雾检测中图像清晰化问题[5]；笔者将基于分数阶微分算子的检测数据融合算法，应用于煤矿监测数据的融合处理之中[6]。 但以上算法只能应用于检测仪器位置固定状态下检测数据的融合处理中，而应用无线传感技术采集井下移动设备检测数据时，因检测设备随着设备一同移动，致使检测数据在测量过程中受多重因素影响，故以上算法无法应用于井下移动设备检测数据的融合处理之中。 本文尝试应用分数阶偏微分方程融合处理井下移动设备的检测数据，并通过在采煤机作业时液压油箱中油温检测数据融合中的应用实验，验证分数阶偏微分方程在井下移动设备检测数据融合处理中有效性。

1 分数阶偏微分方程及其应用

1.1 分数阶偏微分方程

分数阶偏微分方程建立在分数阶微分理论的基础之上，而分数阶微分本质上就是任意阶的分数阶导数。 几百年来，分数阶微分一直缺乏一个严格的定义，当前常用的定义有Riemann-Liouville(R-L)分数阶微分定义、Grunwald-Letnikov(G-L)分数阶微分定义和Caputo 分数阶微分定义[7]，因G-L 定义计算过程相对比较简单，故本文选用分数阶微分的G-L 定义来研究井下移动设备监测信息的处理技术。 分数阶微分的G-L 定义为:

式中:v为分数阶次，为二项式系数，且

现将上述定义推广至二维空间，假设信息采集系统采集到任意给定的二维能量信号S(x，y)，且S(x，y)∈L2(R)，即可得到信号S(x，y)的分数阶偏微分方程:

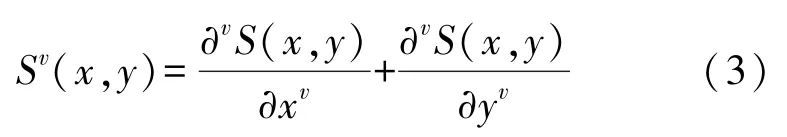
式中:

1.2 分数阶偏微分方程的应用

与整数阶偏微分方程相比，分数阶偏微分方程突出的优势在于它能更好的模拟自然界的物理过程和动态系统过程；与分数阶微分方程相比，分数阶偏微分方程可以将方程中的未知量作为影响因子，实现对方程中多个影响因子的分数阶微分处理。 因分数阶偏微分方程具备以上优点，近年来，对于分数阶偏微分方程特性和应用方面的研究成为了众多专家学者关注的重点，一些研究成果已被广泛应用于温度场分布、图像处理、力学分析和检测技术等领域技术难题的研究之中。 如文献[8]应用分数阶偏微分方程实现了在实际限定条件下高温防护服厚度设计的研究目标；文献[9]通过对分数阶偏微分方程在图像去噪和超分辨率重建中的应用研究，证明了分数阶偏微分方程在图像去噪和减少阶梯效应等方面的优势；文献[10]将分数阶偏微分方程应用于流体力学的研究领域；文献[11]将分数阶偏微分方程应用于离散制造系统检测数据的融合处理技术之中。

2 基于分数阶偏微分的井下移动设备检测数据融合算法

2.1 井下移动设备信息检测数据的特点

假设井下生产系统中存在一台移动设备，为了监测移动设备的实际位置和使用情况，生产管理系统应用物联网技术实时采集移动设备在生产过程中产生的各类信息数据。 众所周知，各类生产信息的采集本质上为实时感知和测量各类传感器发送的能量信号E(t)，故能量信号的检测精度与检测设备性能、工作环境和信息传送能量损失等影响因素息息相关。 在固定设备生产信号检测中，由于设备在生产过程中位置固定不变，各类影响因素在短时间内对生产信号检测精度影响的差异性很小，基本上可以忽略不计。 但在井下移动设备生产信息的检测中，由于设备的位置处于随机变化状态，位置不同检测仪器的工作环境和信号的传送距离就存在着较大的差异性，致使移动设备同一生产信息在不同位置检测时检测误差存在着较大的差异性。

2.2 井下移动设备检测数据的融合算法

为了节约篇幅，假设经无线网路技术采集到的井下移动设备监测信息主要受到仪器性能和信息传输距离两个因素的影响，分别为影响因子x和影响因子y，则信号检测值与影响因子间的函数关系式为J(x，y)。 由于两个影响因子对检测值的影响相互独立，因此函数J(x，y)对于影响因子x和影响因子y的微积分计算方法基本相同。 根据差异化检测数据融合的BVV(Ω)空间函数，可得基于分数阶偏微分方程的物联网下井下移动设备监测信息数据融合算法的变分模型为:

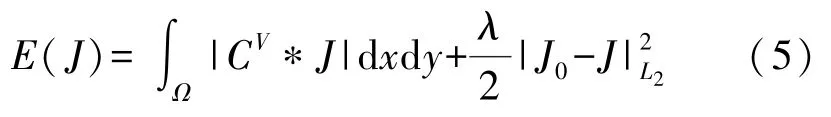
式中:

差异化检测数据表达式的获取，需利用积分离散引导算法的变分法性质构造相应的差异化检测数据的引导函数，假设存在一个任意函数φ，使得以下公式成立:

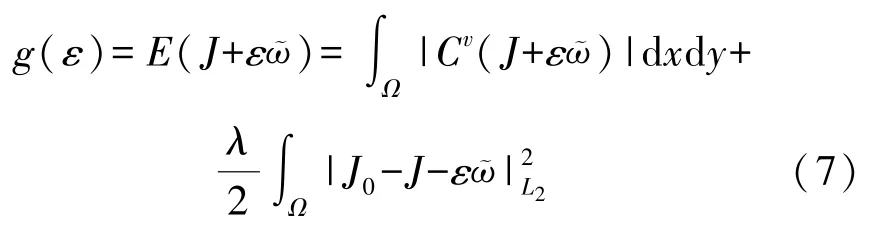
利用泛函极值的基本性质，令g′(o)＝0，可得以下方程:

为了得到最终的差异性检测数据引导模型，需要消除上式中的任意函数φ，采用积分离散引导的差异性检测数据引导模型中的恒等式:

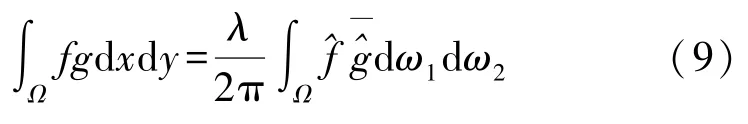
根据积分离散引导的差异性检测数据融合算法的变换性质和函数的任意性，结合式(9)利用差异性检测数据融合算法变分法的基本引理对式(8)进行转换处理，可得:

利用积分离散引导的差异性检测数据融合算法的逆变换可得式(5)所示变分模型的欧拉-拉格朗日方程:

式中:

利用梯度下降法并引入时间t，可以得到G-L定义下基于分数阶偏微分的井下移动设备监测信息检测数据的融合算法模型:

式中:

2.3 井下移动设备监测信息数据的融合处理过程

实现对井下移动设备检测信息处理的前提是实时获取移动设备在工作过程中产生的有效检测数据，随着物联网技术的日益成熟，应用物联网中无线传感网络技术实现井下移动设备监测信息的有效感知和实时采集已不存在技术难题。 首先，数据采集系统根据监测信息的类型，应用相应的传感器有效感知井下移动设备在作业过程产生的监测信息，再应用无线网络实现对所需监测信息检测数据的实时采集；数据采集中心再根据系统设置的检测误差评判检测数据的有效性，如果数据间的误差在系统设置的误差范围内，则将检测数据直接传送至检测系统的数据中心；否则，应用分数阶偏微分方程融合处理检测数据，直至融合后得到的融合数据间误差在系统设置的误差范围内，再将融合后的数据传送至检测系统的数据中心，具体处理过程图1 所示。

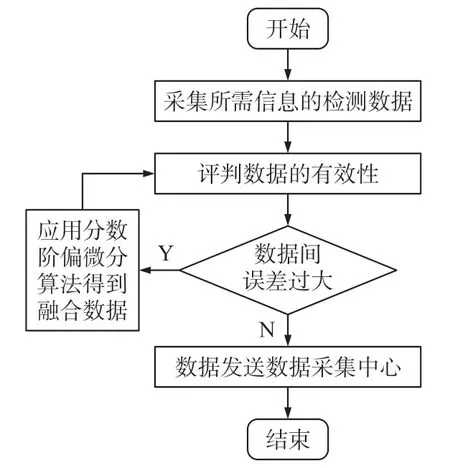
图1 移动设备监测信息数据融合处理流程图

3 算法在井下移动采煤设备监测数据处理中的应用

3.1 实验环境

为了探索井下移动采煤设备检测信息检测误差的形成机理和提高检测精度的科学方法，本案例应用物联网技术实时采集采煤机工作过程中液压油箱油温的监测信息数据，模拟分数阶偏微分方程对采煤机工作过程中液压油箱油温监测数据的融合处理过程。实验地点为淮南某矿地下约700 m 处一综采工作面的采空区。 根据地下空间移动数据源的信息检测特点，本案例采用图2 所示的网络结构实时采集采煤机液压油箱油温检测数据，实验中应用5 只能正常工作的CWDZ11-02-AL-G 型温度传感器测量MG300/730-WD 型采煤机空载运行半小时后，先后采集采煤机距数据采集中心0.20 km、0.25 km、0.30 km、0.35 km、0.40 km 和0.45 km 六处位置工作时液压油箱的油温值，先采用ZigBee 无线网络技术将采煤机的液压油箱油温检测数据传送至井下工作面的数据采集中心，再通过CAN 有线网络将经数据采集中心处理后的检测数据传送到地面上的煤矿生产信息管理中心。 5 只传感器放置在油箱的不同位置且同时工作，在每个采样点间隔5 s 钟取样1 次共取样6 次，取6次检测值的平均值作为传感器在该采样点采煤机液压油箱油温的监测值，则由工作面数据采集中心采集到的采煤机在不同位置工作时各传感器的检测数据如表1 所示。

图2 采煤机液压油箱油温采集系统结构图

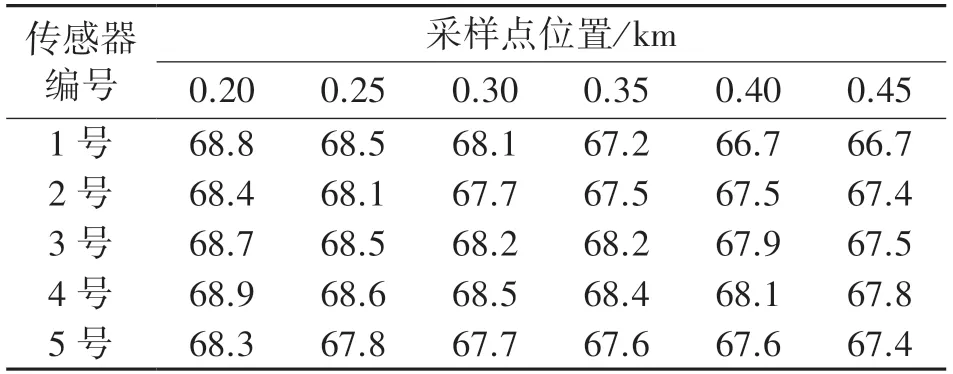
表1 采煤机在不同位置时各传感器的检测数据 单位:℃

3.2 数据分析

从上文的实验环境可以看出，因监测信息需要通过井下远距离无线传输才能到达工作面数据采集中心，故数据采集中心采集到的采煤机液压油箱油温测量值会受到检测设备性能和工作环境等多重因素的影响，设备性能的差异性主要体现在温度传感器间性能的差异性，工作环境的差异性主要体现在信息在无线传输过程中信号干扰和能量衰减的差异性。 结合表1 所示实验数据，将各传感器在不同采样点监测值的平均值作为该传感器对采煤机液压油箱油温的测量值Ji，即可得到表2 所示的各传感器检测数据汇总表；将5 只传感器检测值的平均值作为采煤机在各采样点时采煤机液压油箱油温的测量值Jj，这样就可以得到表3 所示的采煤机在各采样点时液压油箱油温监测值Jj的汇总表。

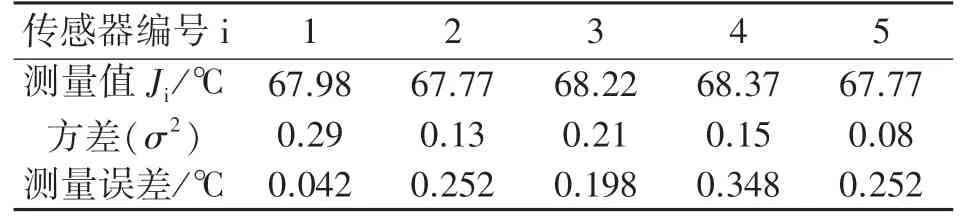
表2 各传感器实验数据汇总表

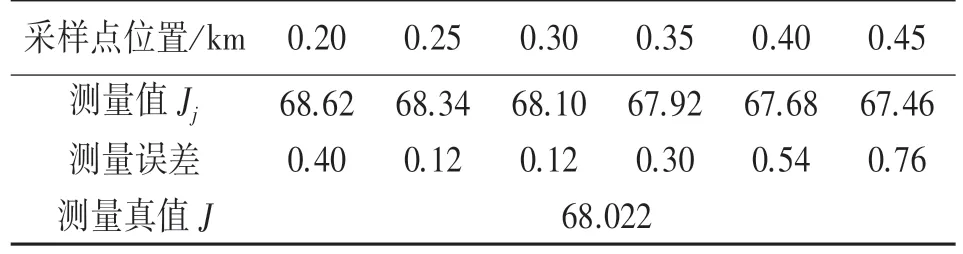
表3 各采样点实验数据汇总表

根据表2 的实验数据可以绘制图3 所示的各传感器检测数据分布曲线，从图3 所示曲线可知:因不同传感器间设备性能存在较大差异性，各传感器对液压油箱油温的检测值离散分布于测量真值附近，致使同一工作环境下不同传感器间的测量误差存在较大差异性。 从表3 所示的实验数据也可以看出:采样点位置不同时传感器的工作环境和信息在无线传送中的能量损失存在差异性，致使同一检测设备在不同采样点间的测量误差也存在较大差异性。 按照常识，采煤机虽处于空载运行状态，但采煤机液压油箱油温应随着时间的推移略有升高，可表3 所示的不同采样点采煤机液压油池的油温值并没有随着工作时间的推移而升高，反而随着工作时间的推移带来检测距离的增加呈现急速下降态势。 因此，本次实验中检测数据间的差异性主要来自于检测仪器间性能的差异性和信息无线传送过程中能耗损失的差异性。

图3 各传感器检测数据分布曲线

3.3 数据融合处理过程

3.3.1 检测值影响因子的选择

根据上文分析，应用5 只型号相同的温度传感器检测采煤机在不同工作位置液压油箱油温时，检测数据间的差异性主要来自于检测仪器间性能的差异性和信息无线传送过程中能耗损失的差异性。 因为方差σ2是衡量检测设备性能的最佳参数，故本案例采用方差σ2作为油温检测值的影响因子x；采样点位于不同工作位置时，检测数据间的差异性主要来自信息传输过程中能量损耗的差异性，检测信息在无线传输时能量损耗与传输距离相关是物理学中的常识，故本案例中将检测信息无线传输距离作为油温检测值的影响因子y，探讨影响因子x、y与采煤机液压油箱油温检测值间的函数关系式J(x，y)。

3.3.2 影响因子与检测值间的函数关系式

①影响因子x与检测值J间的函数关系式

最小二乘法也称为最小平方法，因在函数拟合中无需数据先验信息，且具有较好的数据拟合精度，故被广泛应用于影响因子与检测数据间函数关系式的拟合之中。 因此，本案例根据表2 所示的实验数据，借助最小二乘法求得各温度传感器方差σ2(影响因子xi)与检测值Ji间的函数关系式J(x)，假设测量值Ji及其影响因子xi之间的函数关系式J(x)的数学表达式为:

根据式(14)，可知求出系数ai和阶次n的数值即可获得函数J(x)的关系式。 由最小二乘法的基本定义，可知式(15)所示多项式的阶次应该小于样本数，即n<5。 根据表2 所示实验数据，应用MATLAB 软件中Polyfit 函数，可得出当多项式的阶次n＝1 时，各传感器检测数据的拟合值与测量真值间的误差最小。 此时，检测数据Ji与影响因子xi间的函数关系式为:

②影响因素y与检测值J间的函数关系式

根据无线信号传播理论:在自由空间内，信号的能量损耗与距离的对数(lgy)成正比。 但采煤工作面的工作环境比较复杂，温度、湿度和地形等因素都无法与理想状态下的自由空间相比拟，而且信号在地下隧道中传输时能量损耗还与隧道的形状关系密切[12]。 因此，本案例中需对自由空间中能量衰减公式进行修正处理，根据无线信号室内传输能耗衰减数学公式[13]，则可建立油池油温检测数据J与影响因子y(信号无线传输距离D)间的数学方程式为:

式中:k补偿常数；w为衰减因子。

从式(17)可以看出，检测值J(y)与其影响因子y的对数(lgy)间呈一次函数关系，根据表3 中所示实验数据应用MATLAB 软件中Polyfit 函数拟合出检测值J(y)和lgy间的一次函数关系式，即可得到油温检测数据J与影响因子y间的函数关系式为:

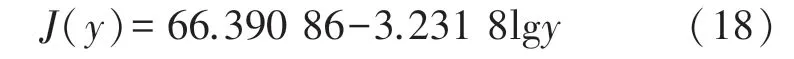
③影响因子x、y与检测值J间的函数关系式

根据上文的分析，可以得知表1 所示实验数据J(xi，yi)为第i只温度传感器在第j个采样点对油池油温的检测数据，这个检测数据既可以将影响因子xi带入式(16)拟合计算，也可以将影响因子yi带入式(18)拟合计算，尽管两种计算方法的计算结果间存在一定的差异性，但差异性不是很大，故可应用数学平均值计算法计算第i只温度传感器在第j个采样点对油池油温的检测数据J(xi，yi)，这样就可以得到检测值J与影响因子x、y间的数学关系式为:

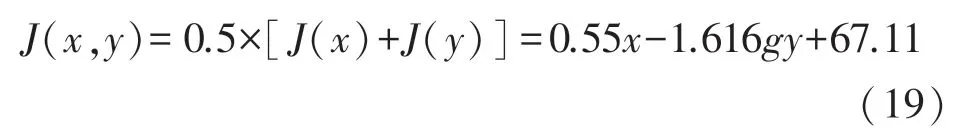
3.3.3 分数阶次v 和步长h 值的选取

根据式(13)，可知获取G-L 定义下基于分数阶偏微分方程的井下移动采煤设备检测数据的融合算法模型的前提是选取式中的分数阶次v和离散步长h的数值。

①分数阶次V的取值

根据分数阶微分算子的幅频特性[14]，可知当微分阶次0

②离散步长h的取值

结合式(13)和式(14)，可以看出:离散步长h的取值直接关系着检测数据间的融合精度和融合速度。离散步长h取值越小，检测数据间的融合精度越高，但数据的融合速度会随着计算工作量的增加而降低。本案例综合考虑融合速度和融合精度两方面因素，根据表2 所示的影响因子x(传感器方差)的取值区间[0.08，0.29]，取离散步长h1＝0.01，需要计算的步数n＝21；根据表所示的影响因子y(信息无线传输距离)的取值范围[0.20，0.45]，取离散步长h2＝0.01，需要计算的步数m＝25。 这样函数J(x，y)对于影响因子x和影响因子y的融合计算步数m、n相近，亦可同时满足计算速度和精度两方面的要求。

3.4 数据融合结果与分析

现将式(19)和相关参数(v、h1、h2、m、n)的数值代入式(13)所示的基于分数阶偏微分方程的移动设备检测数据融合处理数学模型，借助MATLAB 软件即可得到表1 所示的各温度传感器在不同采样点油温检测值J(xi，yj)关于影响因子xi和影响因子yi的0.5 阶偏微分融合处理结果J0.5(xi，yj)，如表4 所示。

表4 测量数据的0.5 阶偏微分融合结果

综合表4 所示的融合结果，我们可以看出采煤机液压油箱油温检测数据经0.5 阶偏微分方程融合处理后，数据呈现以下特点:

①数据的数值明显增大。 表1 中数据经0.5 阶偏微分方程融合处理后数值的平均值为78.26，与融合前的平均值68.022 相比，数值放大了15.05%，说明经分数阶偏微分方程处理后检测信号强度显著增强；

②数据间的差异性明显降低。 将表4 中数据除以增强系数1.150 5，可知融合后的检测数据最大值与最小值间的误差不到0.4%，远小于融合前的2.65%；绘制图4 所示的融合后各传感器油温检测数据分布图，可以看出融合后的检测数据随机的分布在测量真值附近，与图3 相比，数据间的离散性大幅降低。

图4 各传感器检测值经0.5 阶偏微分融合后数据分布图

为便于比较分数阶偏微分算法与其他算法对煤矿移动采煤设备检测数据的融合精度，现将表4 中各传感器的融合结果除以增强系数1.150 5，可得出应用0.5 阶偏微分方程融合处理后，采煤机液压油箱的油温检测值间的标准差为0.045，大幅小于卡尔曼滤波算法的0.21 和平均值法的0.48，说明分数阶偏微分算法对于井下移动设备的检测数据具有较高的融合处理精度。

4 结论

无线传输是井下移动设备监测信息的主要传输方式，而无线网传输过程中因检测设备性能、信号干扰和能量损失导致信号失真是信息检测系统面临的主要技术难题，致使物联网下井下生产信息管理系统采集到的井下移动设备监测信息检测数据，必然会受设备性能、工作环境和信号干扰等多重因素的影响，存在着难以预测的测量误差。 本文针对分数阶微分算子具有较高的数据融合精度，但无法同时实现对多个影响因子的融合处理的不足，将分数阶微分算子拓展至分数阶偏微分领域，建立了基于分数阶偏微分方程的移动设备检测数据融合算法模型，并通过该算法在井下重要采煤设备-采煤机工作时液压油箱油温检测数据融合处理中的应用试验，验证了分数阶偏微分对于井下移动设备检测数据融合处理的有效性。 实现了以低成本对井下移动设备监测信息的快速、高精度检测研究目标。 研究成果对于提升井下移动设备检测数据的准确性和生产管理系统工作的可靠性具有重要的实用价值。