基于MEMS 电容式加速度计的闭环读出电路设计∗

徐 娇张玉龙杨中宝吴次南刘泽文∗

(1.贵州大学大数据与信息工程学院，贵州 贵阳550025；2.清华大学微电子学研究所，北京100084)

加速度计在汽车、手机、航天航空等领域具有广泛的应用。 市场对加速度性能、功耗和尺寸的要求越来越高。 现代集成加速度计通常由传感器与读出电路两个部分组成，传感器将得到的加速度转换成电流、电容等电学信号。 读出电路将所得到的小信号经过一系列处理，输出所需要的、便于检测的与加速度成比例的信号[1]。 所以，读出电路的品质对微加速度计的性能有很大的影响，包括噪声水平、线性度和动态范围。 将传感器和读出电路作为一个系统进行设计，对实现高性能加速度计具有重要意义。

有许多文献对传感器的建模和仿真进行了研究，仿真方法有SIMULINK 电模型、SIMULINK 数字模型[2]、COMSOL 有限元分析等[3]；读出电路结构有开环结构、闭环结构，闭环结构有时分力反馈模型、Σ-Δ闭环检测模型等。 时分力反馈电路结构将连续时间转换为离散时间并进行仿真，仿真结果与连续时间模型一致，但实际电路中结构占用面积大、结构复杂[4]；Σ-Δ闭环检测电路结构仿真中只有高阶结构性能优势，可用于提高动态范围等性能[5]；闭环结构较开环结构具有明显的灵敏度及线性度优势[6-7]，虽占用面积较大，但结构简单。

利用MATLAB SIMULINK 仿真是目前加速度传感器仿真设计的最常用方法。 Biter Boga 等人在设计读出电路时考虑到了噪声参数的因素影响，并得到总噪声为58.7 μg/[8]；Alice Lanniel 等人在传感器中分析了寄生参数对稳定时间的影响[9]；Qian K 等人研究的传感器为梳齿不对称性的结构[10]，并得到理论电压灵敏度为2.02 mV/gn，电压灵敏度误差小于2%。 加速度传感器的信号检测有多种方式[11]，包括谐振式、压阻式、隧穿电流式、电容式等。其中闭环反馈电容式检测方法具有稳定性好、精度高的优点。 本文所设计的闭环反馈读出电路由差分电容器、电容电压转换器、采样保持电路、PID 比例积分微分调节器以及二阶低通滤波器组成。 对所设计的传感器及读出电路用MATLAB SIMULINK 进行系统级别的建模与仿真。 为了全面分析加速度计传感器结构及其读出电路对加速传感器性能的影响，设计仿真中考虑了圆片级封装的寄生参数、噪声影响及工艺导致的梳齿结构不对称等因素。

1 电容加速度计结构及其原理

加速度计的传感器结构图如图1 所示。 它是由质量块、两个蛇型弹性梁以及18 组梳齿所构成的。当有加速度作用于质量块时，梳齿间的距离发生变化，从而导致了电容的变化。

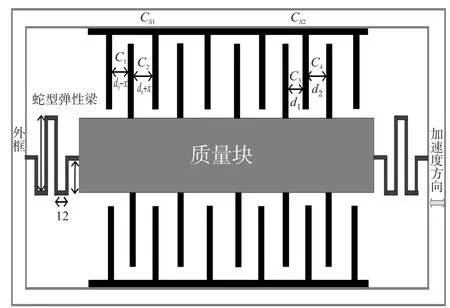
图1 加速度计传感器结构

加速度计传感器的质量块的运动学方程可表示为:

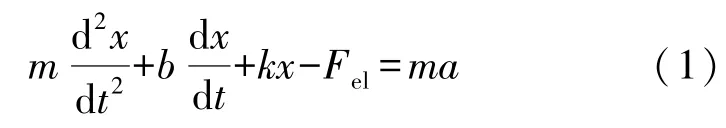
式(1)经过拉普拉斯变化为:

式中:m为质量块的有效质量，a为外部的加速度，b、k、Fel分别为阻尼系数、弹性系数和静电力；w0为系统的固有频率。 因此，可得到阻尼系数:

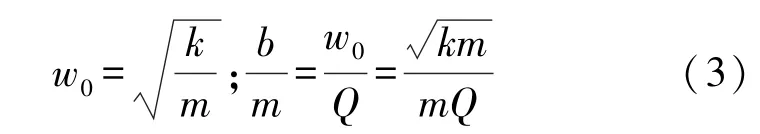
如图1 所示，此加速度计结构是由两个蛇型弹性梁组成，用来固定支撑质量块；它的弹性系数，如式(4)所示:

式中:E为结构材料的杨性模量，t为结构层厚度。

2 梳齿结构分析

2.1 对称结构

如果结构中的梳齿是对称的。 如图2 所示，无加速度时，系统处于平衡，梳齿间距离都为d0，此时电容值如式(5)所示；当有加速度作用于质量块时，梳齿间距离发生变化，电容值变化如式(6)所示(x≪d0)；电容差值如式(7)所示。

图2 加速度计原理图

如果分别在固定电极C1FE、C2FE加上交流电压v1、v2。 那么下面的静电力作用在移动电极板上如图2 所示。

2.2 不对称结构

在实际实验制作中，由于工艺的影响，梳齿结构很可能会发生不对称性，当梳齿不对称，则差分电容、静电力都会发生改变。 为了分析工艺对性能的影响。 假设一共n对梳齿电容，由式(5)～式(7)可得到，并用泰勒展开可表示为:

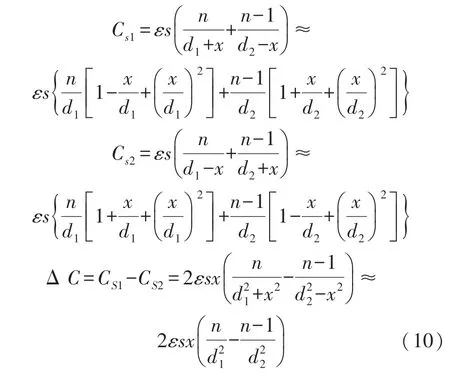
由式(9)、式(10)得到此时的静电力为

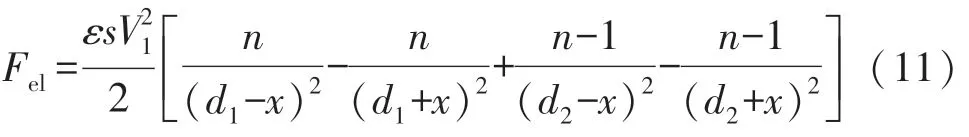
将d1、d2的值设为三组对比数据分为d10、d20；d11、d21；d12、d22，其值如表一所示，并进行仿真对比分析。

3 加速度计及其读出电路等效电路的仿真模型

速度计的等效电路图如图3 所示，由差分电容器、电容电压转换器、采样保持电路、PID 比例积分微分调节器、二阶低通滤波器及反馈电路组成。

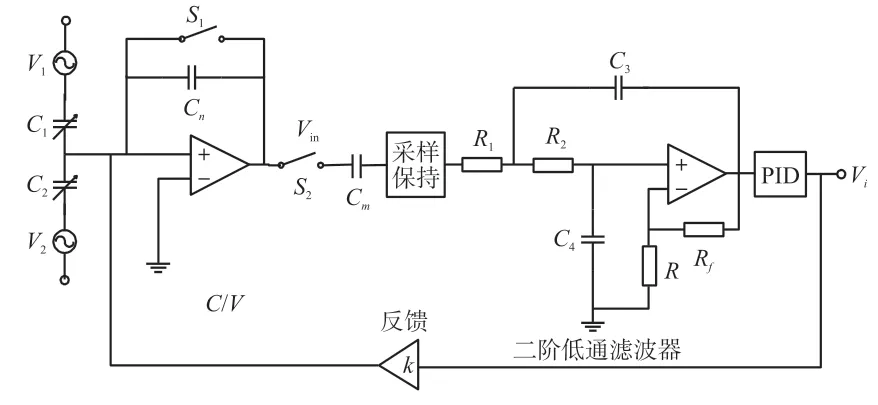
图3 读出电路等效电路图

3.1 寄生参数及噪声分析

3.1.1 寄生参数

在实验制作和封装过程中，传感器及读出电路会产生很大的寄生电容。 所以在仿真过程中需要将寄生电容Cm考虑在电路里。 由图3 可得如下方程:

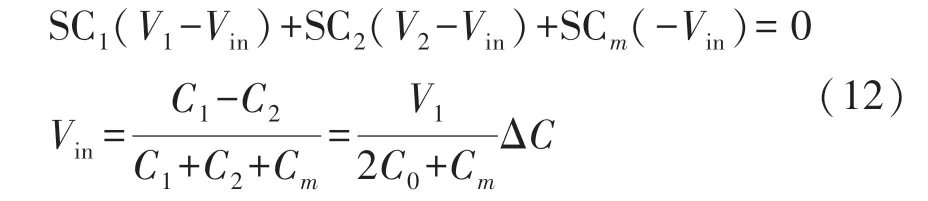
圆片级封装，即将传感器与读出电路封装在一个芯片里，减少了传感器与读出电路的导线连接长度，从而减少了寄生电容。 不同的封装会产生不同的寄生参数。

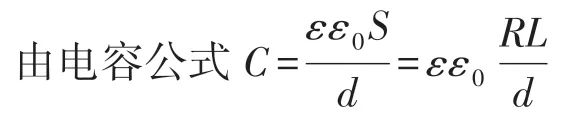
ε:介质介电常数；ε0:真空介电常数；S:电极板正对面积；R:导线直径；d:导线到衬底的距离都为0.05 μm；L:导线长度。 若圆片级封装的导线长度L1为0.5 mm～1.0 mm，普通封装的导线长度L2为10 mm～20 mm。

可以得到，圆片级封装的寄生电容较普通封装减少10 倍～20 倍。 即圆片级封装的寄生电容为4 pF～8 pF，普通封装的寄生电容为40 pF～80 pF。

3.1.2 噪声分析

不同的噪声源会对加速度计产生不同的影响，所以对闭环电路来讲，需要对布朗噪声、放大器噪声及开关噪声考虑分析。

布朗噪声是由于质量块的热运动产生的，在系统中为白噪声输入[12]，它表示为

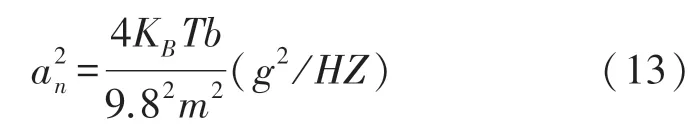
放大器噪声由热噪声和闪烁噪声组成，通常来讲，使用双相关采样可消除闪烁噪声[13]，所以放大器噪声可表示为

fs为采样频率；

KT/C 噪声是电路中主要的噪声源之一[14]，其可表示为

3.2 SIMULINK 模型

本文采用二阶低通滤波器对读出电路进行处理，所采用的二阶低通滤波器的基本原理图如图3所示[15]；二阶低通滤波器的传递函数如下所示:

式中:Auf为通带增益；Q为等效品质因数；wn＝:特征角频率。 当Auf<3 时，滤波器才能正常工作，本文中的参数为Auf＝1.58；R1＝R2＝160 kΩ；C1＝C2＝1.2 nF；a2＝1/w2n＝0.000 192，a1＝1/Qwn＝0.009 796。

当系统在平稳状态时，质量块的位移x必须为零，所以此时需要具有传递函数功能的比例积分微分调节器；因为系统采用的是闭环反馈结构读出电路，灵敏度及线性度性能较好。 当零加速度作用于系统时，采用静电力作为反作用力，才能使质量块在两电极处处于平衡状态。

采用SIMULINK 对读出电路进行建模仿真，如图4 所示。

图4 SIMULINK 模型

4 仿真及结果分析

本文所采用的结构和参数如表1 所示。

此读出电路的输入加速度信号、输出电压信号随采样时间的变化如图5(a)中的a、b 曲线。 传感器质量块位移输出、差分电容输出与加速度输入间的关系如图5(b)所示。

从图5(a)可以看出，当输入正弦的加速度信号时，质量快位移和电压信号的输出具有一致的时变特性。 为了验证本仿真的正确性，曲线c给出了利用F. Chen 在2017 年所发表的文献[16]中的参数仿真得到的输出电压信号，可以看到，采用我们的仿真模型所得到的结果与所发表的文献结果一致。 从图5(b)可以看出，位移输出、差分电容输出与加速度输入成线性关系。 电容灵敏度0.270 fF/gn。

表1 参数

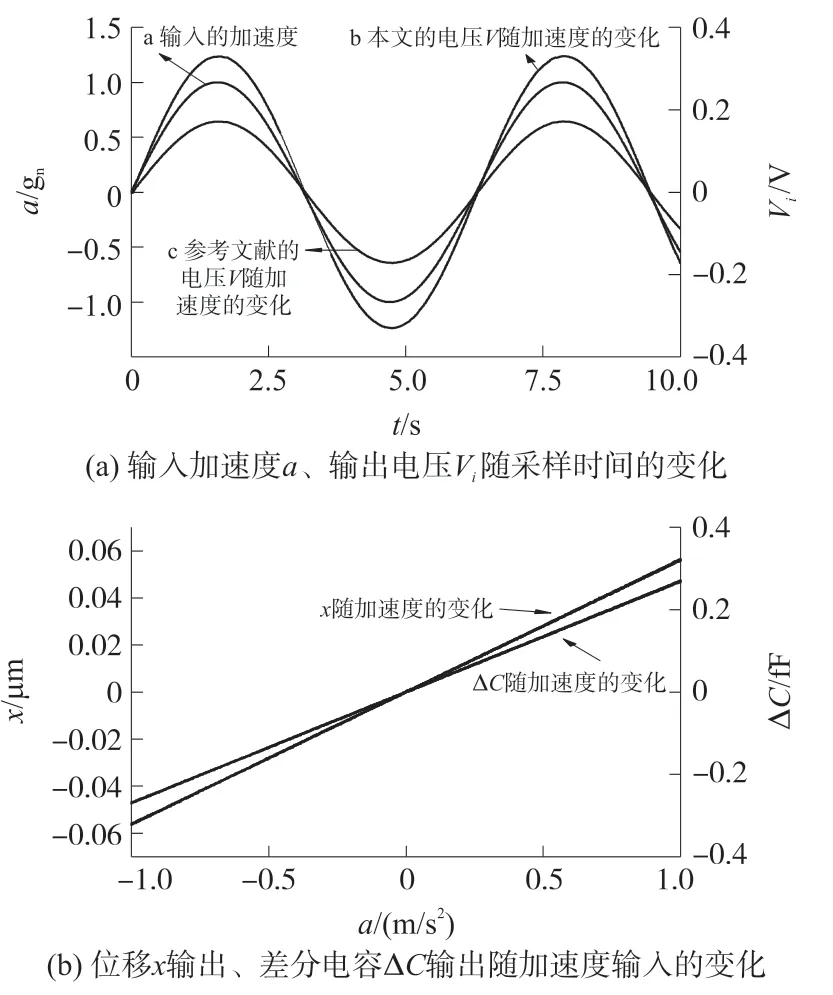
图5 输入加速度a 与输出电压Vi 随采样时间的变化和位移x 输出与差分电容ΔC 输出随加速度输入的变化

加速度a输出随位移x输入的变化如图6 所示。

从图6 可以看出，位移在±1 μm，即梳齿振动为梳齿间距1/10 左右，该图表明利用我们的结构参数设计出的加速度量程为±20 gn。

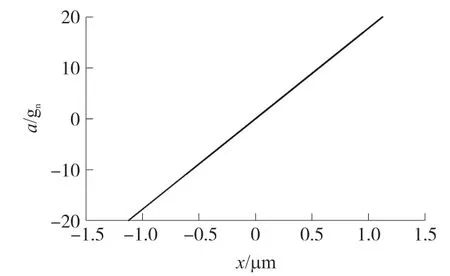
图6 加速度a 输出随位移x 输入的变化

为了考虑工艺所影响的梳齿结构，对对称梳齿及不对称梳齿进行仿真分析。 对称梳齿结构和不对称梳齿结构的输出电压与输入加速度之间的关系如图7 所示。 曲线C、D、E、F分别为传感器的对称梳齿结构、不对称梳齿结构d10＝8 μm；d20＝10 μm、不对称梳齿结构d11＝6 μm；d21＝12 μm、不对称梳齿结构d12＝4 μm；d22＝14 μm 的电压输出随加速度输入的曲线。

图7 对称梳齿结构、不对称梳齿结构的非线性误差对比

从图7 中可以看出，非线性误差均在0.5%内，非线性误差随着不对称结构的梳齿间距离差值的增加而逐渐变大。

圆片级封装与普通封装的输出电压与输入加速度之间的关系如图8 所示。C、J曲线分别为圆片级封装、普通封装。

图8 圆片级封装、普通封装的非线性误差对比

从图8 中可以看出，本电路设计中，普通封装和圆片级封装的非线性误差均在0.5%内，普通封装的非线性误差大于圆片级封装的非线性误差。

圆片级封装与普通封装的稳定时间如图9 所示。 从图9 可以得到，圆片级封装的稳定时间在2 ms，普通封装的稳定时间在4 ms。

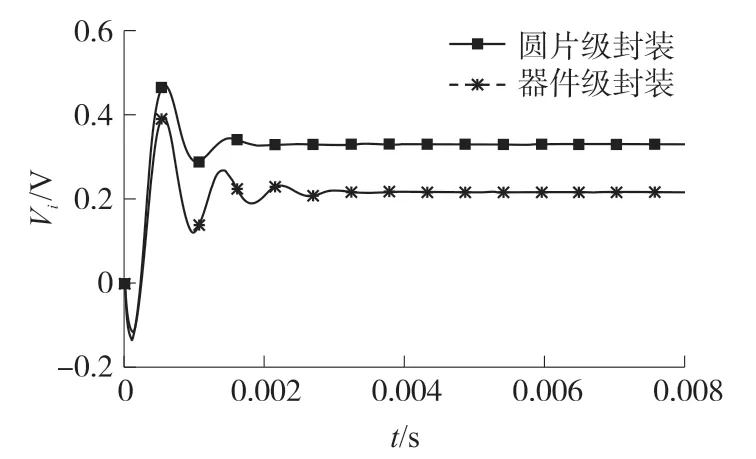
图9 圆片级封装、器件级封装的稳定时间对比

5 结论

由电容式加速度计传感器的运动学理论与基本原理，设计了一款闭环反馈读出电路系统仿真模型。在SIMULINK 仿真过程中分析了噪声、圆片级封装与普通封装的寄生参数比较及实际工艺中流水结构的不对称性。 结果表明，位移、差分电容以及输出电压是与输入加速度成线性关系的；所设计传感器及读出电路的非线性误差在量程±20 gn范围内小于0.5%；且对称梳齿结构的线性度优于不对称梳齿结构，随着不对称梳齿的距离差值逐渐增大时，非线性误差也在逐步变大；圆片级封装的非线性误差小于普通封装的非线性误差。 圆片级封装的稳定时间在2 ms，小于普通封装的稳定时间；基于圆片级封装的对称性梳齿结构的输出电压灵敏度为328 mV/gn。

此读出电路模型可减小非线性误差。 为提高传感器性能，在实际工艺中，应将梳齿尽量对称化进行圆片级封装。