正则化ISU-LSTM 的多传感器故障预测方法

王家能周治平

(1.江南大学物联网学院，江苏 无锡214122；2.江南大学物联网技术应用教育部工程研究中心，江苏 无锡214122)

工业4.0 时代背景下，工业多传感器信息物理系统(CPS)实现了网络计算和传感网络的协同运行[1]，将工业网格化的传感设备带入智能控制时代。 随着CPS 传感系统的广泛使用，故障检测和运行维护在当今工业环境下具有非凡意义[2]。 为了确保CPS 传感系统能够平稳运行并且得到实时的安全性能反馈信息[3]，建立实时故障监测健康管理系统(PHM)[4]成为新的研究热点。

CPS 各子系统配备有网络化布局的传感器，自动化生产线会产生大量实时传感器数据，深度学习处理这些数据可以凸显其计算优势[5]。 近年来，基于神经网络的可靠预测方法在传感器故障检测领域得到广泛应用[6]。 Zhang 等人提出了一种多目标进化集成学习框架和DBN 算法相结合的剩余使用寿命方法，取得较好性能[7]。 Wu 等人结合LSTM 和动态差分特征建立发动机RUL 预测模型[8]，根据动态差分系数提高预测精度。 Namuduri 等人重点研究工业传感器的故障预测，使用LSTM 网络获得较高的准确性[9]。 在健康管理PHM 研究上，Wang 使用相似评估方法在对多传感器故障预测领域十分有效[10]。 Guo 等人基于回归神经网络设计传感故障预测指示模型，充分利用回归网络的反馈优势，准确预测故障警报时间[11]。 为了凸显神经网络的计算优势，更多的研究趋向于对神经网络的改进。 Yu 等人改进了双向回归神经网络，将自编码器结构融入其中[12]。 Verstraete 等人采用半监督式的深度对抗算法有效解决多传感器领域的系统维护，准确预测故障时间[13]。 Zhang 等人从系统的动态性能出发，建立LSTM 的系统寿命预测模型，对实时数据进行准确预测[14]。 传统传感器系统故障预测方法无法有效屏蔽无用信息的影响，无法满足现代CPS 系统多传感器的实时性要求。

工业传感器系统出现故障的过程和时间的推移有密切关系，是缓慢的累积过程[15]。 因此，建立具有准确实时性的故障预测模型，要从时间序列角度出发，提取影响因子较高的序列信息[16]。 传统LSTM 在处理工业大数据集时存在如下问题:①神经网络在提取CPS 传感器系统大量长序列的特征信息时，无法准确捕捉传感器的噪声信息并对其进行屏蔽，使其处理效率低下。 ②实际传感信息融合系统的故障预测模型对实时性要求较高，而传统方法无法对海量数据进行在线更新，在故障真实发生时，很难对控制中心发出及时反馈警报[17]。

针对传统方法存在的问题，本文主要从稀疏神经网络结构的角度出发，满足实时性要求，减少网络训练的计算量[18]。 本文设计的模型包含三个部分:①首先介绍实际场景中多传感器模型以及瞬态故障类型；②其次设计内置稀疏单元，实现神经网络快速计算，使用稀疏单元改进传统遗忘门，建立内置稀疏单元的长短时记忆网络(ISU-LSTM)预测模型；③最后设计故障预测的在线监测系统，在系统运行中时刻监测其安全性能。

1 多传感器模型

含有拓扑传感结构的CPS 系统的数据传输流程:传感器测量到的物理数据传输到控制中心，控制中心得到该数据信息，使用故障预测算法计算得到决策结果并且反馈给与之耦合的执行器，最终执行器执行最后的决策结果并且做出故障警告，完成全部故障预测流程。

本文研究对象是测量相同变量的多个传感器组成的CPS 系统，该系统以周期性的形式(T)采集传感器上传的数据，完成模型训练和在线更新预测模型。 根据已知的动力学公式，建立CPS 离散线性时不变系统:

式中:定义xt＝(xt1，xt2，xt3，…，xtn)∈Rn为t时刻状态，ut＝(ut1，ut2，ut3，…，utp)∈Rp为控制系统的输入数据；yt∈Rm为输出数据；ωt∈Rq和vt∈Rl分别为干扰数据和系统噪声；A∈Rn×m、B∈Rn×p、C∈Rm×n分别是系统的状态矩阵、输入和输出矩阵。

传感器模型的抽象区间定义了传感器测得数据的精度范围，每个传感器测量特定物理对象的数值在一定区间内[Si(t)-δi，Si(t)＋δi]，Si(t)表示t时刻传感器测量值，δi表示容错度，容错度越小表示传感器的安全性要求越高。 传感器Si在t时刻真实值表示为τi(t)，如果测量值与真实值的偏差在容错范围之外，则定义在t时刻传感器发生故障。

定义1(故障依据) 本文用传感器测量与真实的差值δ(Si，t)作为衡量传感器是否发生故障的依据。

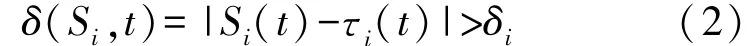
式(2)中表示二者差值超出容错精度范围，此时定义传感器发生故障。

定义2(假阳性故障) 第i组传感器的假阳性故障并非真实故障，由三元组构成:(δi，ξi，wi)，δi是容错度，(ξi，wi)是假阳性阈值，其值表示在任意时间范围为wi的窗口中存在ξi个测量故障值。 假阳性阈值(ξi，wi)定义假阳性故障和真实故障边界值，在任意wi区间范围内，故障点小于阈值的现象称为假阳性故障，反之为真实故障。 假阳性故障F(Si，t)用式(3)表示:

故障检测仅考虑阳性故障的节点，因此，传感器Si系统在运行过程中至少出现一次阳性故障，即可称之为此时发生真实故障。 算法目标就是排除假阳性故障和无故障，准确预测真实故障节点。

2 ISU-LSTM 故障预测算法

ISU-LSTM 网络集中研究了稀疏长短时记忆的网络结构。 预测模型分为2 步:离线预测模型和在线监测，满足传感器运行中对实时检测的要求。

2.1 正则转换门的稀疏原理

现有多传感器系统生产中得到的时间序列数据存在较大的噪声干扰，快速网络中的稀疏门控单元高度识别噪声信息和有效信息，排除假阳性故障。

2.1.1 内置稀疏单元ISU

ISU 单元包含双门结构:直通门(P 门)和正则门(R 门)，如图1 所示。 P 门允许权重因子大于初始化阈值权重的数据通过门控单元；R 是正则门，该门控单元需要数据进行正则变换计算选择性通过，建立选择性机制，排除假阳性故障的影响。

在ISU 单元当中，双门结构协调联动工作，稀疏门控单元的输出由两部分叠加组成，定义神经元的输出y，输入为x。 可从式(4)中看出:

图1 门控结构图

式中:σ(·)是sigmoid 激活函数，WR表示转换门的权重矩阵，br表示故障偏置。

xt表示传感器输入信息，P(xt，WP)是P门的直通函数，二者乘积得到P门输出端口信息；H(xt，Wh)是非线性变化权重矩阵，R(xt，WR)是R门的正则函数；根据式(4)可得到神经元的激活度Sf。 ISU结构单元如图2 所示。

图2 ISU 示意图

本文设计的门控单元实质上是对输入信息矩阵[ht-1，xt]的权重输出表示，当门控函数是0 时，表示该神经元的偏置和权重矩阵在此次训练中没有得到故障更新训练；反之为1 时表示传感器信号全部通过稀疏门控单元；当门控单元属于半开半闭状态下对传感器信号进行权重筛选，排除假阳性故障，捕捉潜在故障节点。

2.1.2 转换门正则化

对于潜在的真实故障数据，本文采用正则化的方法对其进行训练。 正则化用组套索正则化的方法来实现变量组的稀疏，使得变量组别同时为零或同时不为零。 组套索正则化方法将一个神经元的所有输出权值作为同一组，用优化算法将输出权值全部排除。

套索正则化方法的核心内容是考虑三个组级的稀疏性:输入组Gin、隐藏组Gh、偏置组Gb。 输入组是所有传感器输入xt构成的向量，隐藏组是所有隐藏层神经元ht构成的向量，偏置组是对应网络中偏置bR的一维组，输出神经元为y。 三种组级的权值分组策略如图3 所示。

图3 组套索正则化示意图

组稀疏正则化可表达为:

式中:｜g｜是传感器向量g的维度，它保证了每个组都得到统一加权。 相对于l1范数的次优解稀疏方法，式(5)中对于正则化表示采用的是绝对值的形式。 此方法优势在于让更多的传感器系数归结为0，模型参数估计对多传感器进行变量选择，加快收敛速度。 因此，组稀疏正则化用标准一阶优化获得较好的收敛性。

最后，总结出稀疏组套索惩罚(SGL)分别由l1和l2，1惩罚项的叠加构成:

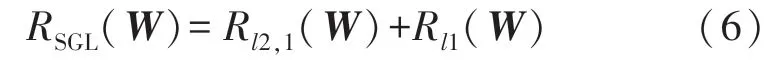
SGL 惩罚与构成它的范数具有相同的性质，通过式(6)即可输出稀疏正则化门的最优故障解。

2.2 离线ISU-LSTM 预测算法

长短时记忆网络具有时间顺序的关联性特点，将传感器序列特征传入LSTM 网络中计算得到隐含层输出。 接着通过隐含层和全连接层的关联获得N_classes 分类结果，最后通过softmax 函数预测出传感器故障信息。

网络结构示意图如图4 所示，在单一LSTM 网络神经元中，含有三个输入，分别是上一时刻的长期记忆单元Ct-1、短期记忆单元Ht-1和传感器输入信息Xt。

内置稀疏单元LSTM 网络分为三个阶段，第一阶段是稀疏遗忘阶段，上一层神经元输出的信息输入到该单元时，记忆单元Ct-1将会遗失部分内容。用式(7)表达为:

图4 嵌入稀疏单元的LSTM 模型

式中:WRx和WRh分别表示对传感器信号Xt和隐藏层长期记忆单元Ct-1的权重矩阵，bR是R门的偏置，σ(·)是sigmoid 激活函数。

内置稀疏单元输出结果ft取代遗忘门输出，ft与上层神经单元的长期记忆单元点乘来排除假阳性信息，其中⊙是元素点乘。 用式(8)表示:

第二阶段是输入选择阶段，此阶段对短期输入信息进行筛选，差值超出容错度的传感器信号元素权重会比假阳性信号大，用式(9)表示:

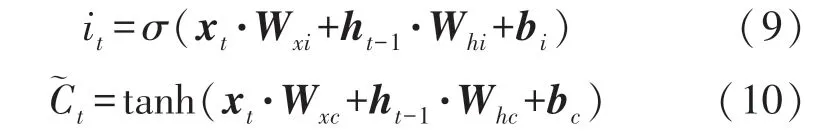
双曲正切函数tanh 对输入信息Xt进行缩放处理，计算出当前时刻的长期记忆单元Ct:

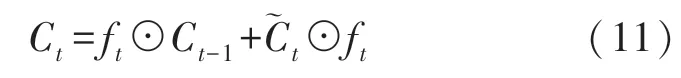
第三阶段是输出汇总阶段，该阶段对稀疏阶段的传感器信息进行汇总，用式(12)表示:

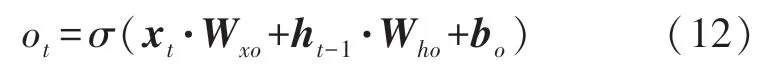
该阶段最终输出是由长期记忆单元和输出门的输出ot决定，用式(13)所示:

tanh(·)表示双曲正切函数。W表示权重矩阵，通过权重矩阵，输入更新ut与三个门(it，ft，ot)用变量隐藏层单元ht-1和输入xt来表示。

最后，将模型的输出ht采用softmax 函数回归的方式得到故障预测结果的概率分布:

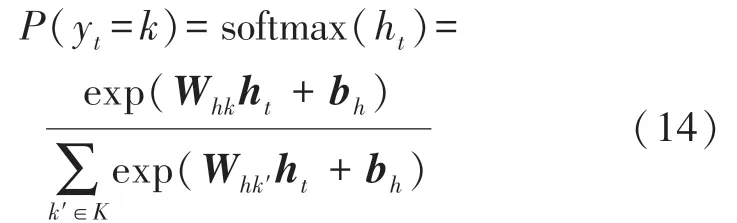
K表示故障预测结果分类区域，K＝[0，1](0 表示正常特征)。

整个模型得到的最终预测故障yt用式(15)表示:

2.3 系统故障在线监测模型的实现

本文设计故障预测的实时监测模型的目的是建立逐步优化的神经网络架构，能够对传感系统进行实时在线维护。 实时监测系统采用均方根误差(MSE)作为优化指标，对网络层参数进行优化，通过迭代实现故障预测结果和实际故障警报时间相一致，排除假阳性故障。

本文将输入的传感器样本分为两类X1和X2。X1作为训练数据，在每层神经元中得到隐含神经元的记忆单元ht和传感器标签Lt直接的转换关系:

A表示两者之间的转移矩阵，它代表了神经元记忆单元和传感器标签之间一一映射。 经过一定矩阵变换得到映射转移矩阵A的表达式:

根据不断深入的网络隐藏层和传感器标签得到相对应的映射转移矩阵。 针对测试数据L2，神经网络根据隐藏层之间的关联参数θ＝{W，a，b}，得到t时刻隐藏层神经单元状态ht，结合训练样本中得到的映射转移矩阵A，表达出测试样本L2表达式:

L2是网络测试中得到的预测值，表示传感器真实值，虽然实时传感器数据没有标签，但通过缩小MSE 的方法实现测试优化，获得更趋近真实的数据曲线。 用式(19)表示:

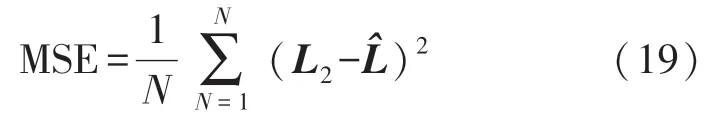
N表示传感器总维数，通过不断缩小MSE 的值来优化网络隐含层的参数，在更新中获得最优映射矩阵。

本文设计的实时传感器监测系统框图如图5 所示，实时监测模型具体实现步骤如下:

步骤1 对传感器信号进行傅里叶变换，并对其进行归一化处理，得到统一的幅值数据。

步骤2 初始化神经网络中的参数:容错度δi、假阳性阈值(ξi，wi)、均方误差阈值MSEmax、权重矩阵Wh、偏置b等，设定合适的迭代次数和误差阈值等超参数值。

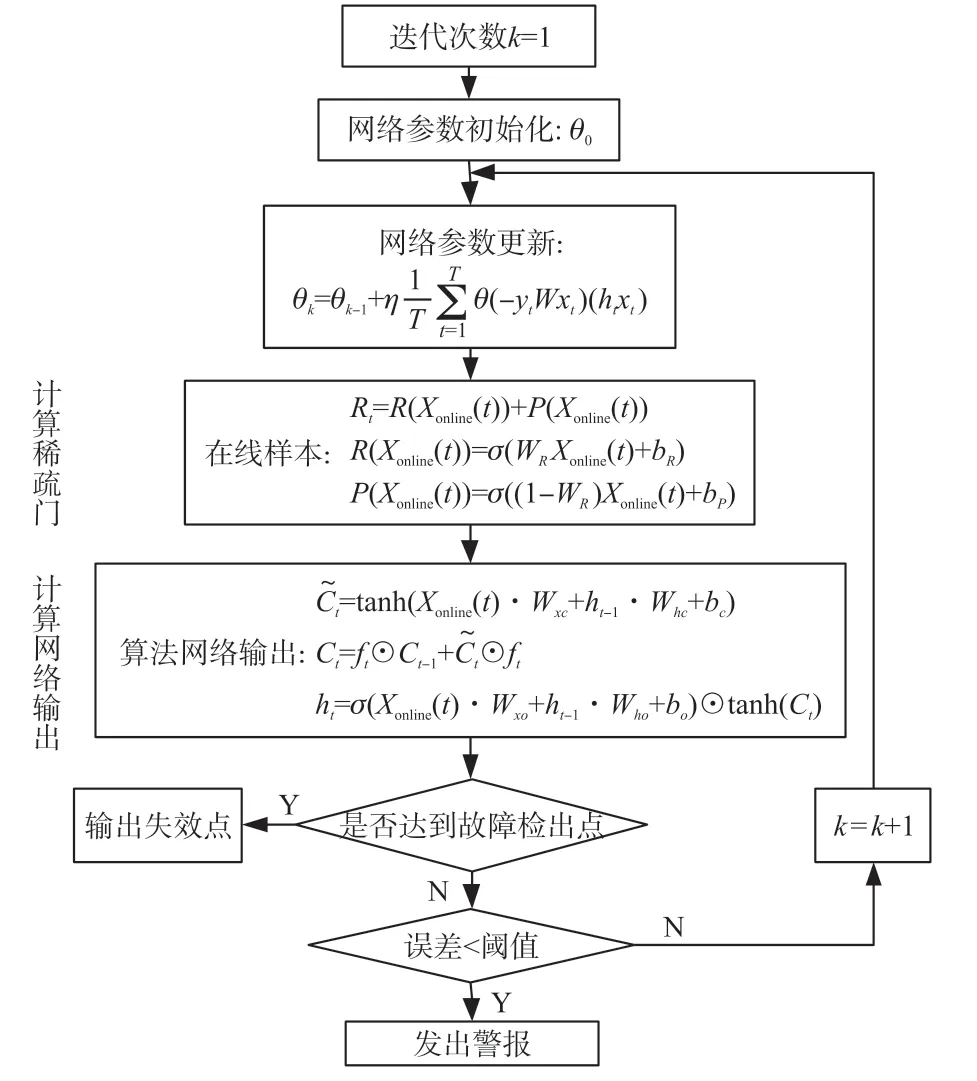
图5 实时监测系统流程框图

步骤3 根据部分传感器数据和真实标签训练原始网络，获得初始全监督预测网络。

步骤4 将实时周期数据作为输入，根据式(13)得到输出信息ht。

步骤5 根据当前时刻预测值与下一周期真实值的均方误差公式得到不同时刻的均方根误差指标MSE。

步骤6 在训练下一采样周期的实时数据时，将已训练好的网络作为该周期的初始预测模型。 使用最小化均方误差的方法迭代更新网络参数；

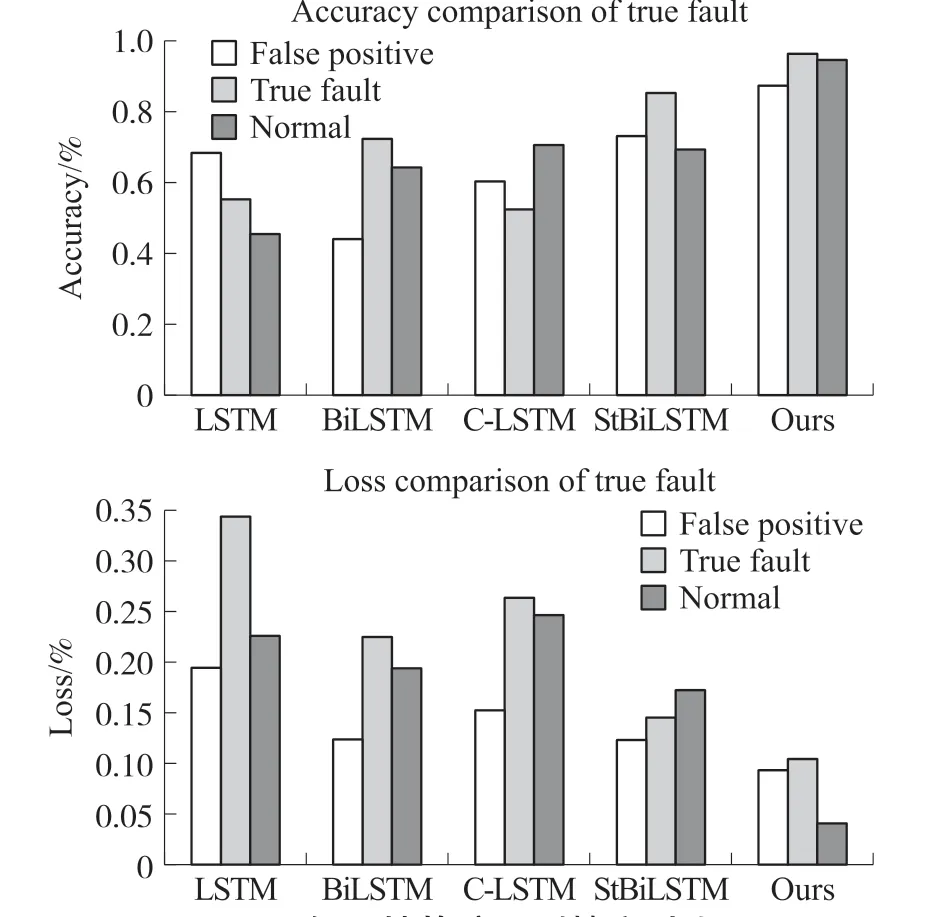
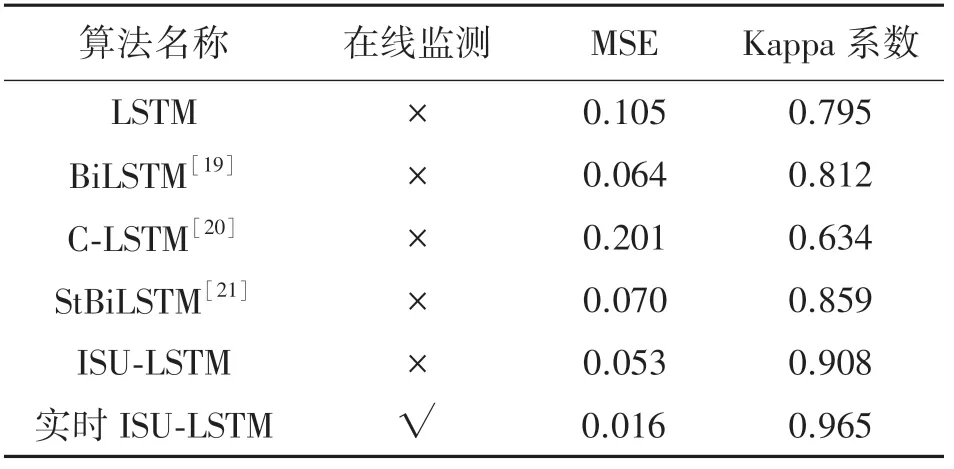
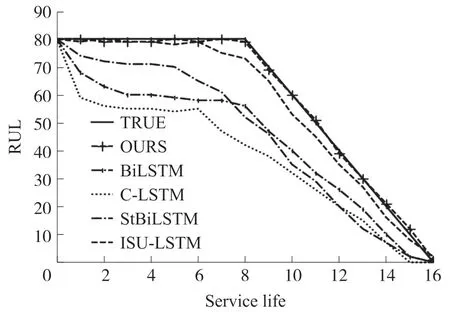
步骤7 假如符合条件MSE

步骤8 不停迭代直到预测值与真实值吻合，此时确定故障信息预测值并且对控制中心传递警报信息。

通过本文算法训练数据集，得到前向运算值MSE。 将实时MSE 值来与参数初始化的阈值进行比较，通过不断迭代减小误差结果，获得最优的故障预测结果。

3 工业CPS 系统故障仿真测试

本文首先通过仿真传感器数据进行算法的有效性分析，通过真实的案例研究对算法的有效性进行验证。 实验数据集为预测与健康管理国际会议(PHM08)上举行的数据挑战竞赛上CPS 传感器相关数据。 本章通过与改进神经算法预测模型进行对比来验证提出方法的有效性，与LSTM、文献[19-21]中BiLSTM、C-LSTM 和StBiLSTM 等经典预测传感器RUL 模型的对比。

3.1 算法参数选择

故障预测模型的核心部分是对系统的剩余使用寿命的准确预估。 RUL 的数值实质上是一种概率统计数据，其预测模型的输入是传感器的数据提取特征。

用式(20)表示RUL 数值:

TEOL是多传感器系统退化到故障阈值的生产总周期；TECL表示多传感器系统当前时刻已经运行的周期，即RUL 的检测起始点。 网络训练时的初始化参数如表1 所示，模型参数的选择依据相关文献[8]LSTM 网络的常规化初始数据，偏置参数的初始值选用为0。

表1 神经网络ISU-LSTM 模型参数

输入输出维度依据所选用的多传感器系统数据集的维度，对于18 个传感器，标号为1、4、5、13 和15的传感器在运行全过程中测量具有恒定值，证明传感器测量数值与发动机退化无关。 将剩余13 位传感器数据作为预测模型输入，最终得到一维真实故障概率发布P(yt＝k)。

3.2 预测性能分析

为了模拟真实场景下的故障检测场景，本文选取每个传感器数量都是随机的，每个维度传感器选用400 个测量数据。 为了获得鲁棒的假阳性故障模型参数，降低实验结果的偶然性，实验采用随机任意的时间窗口进行训练和测试。 表2 中发现本文算法采用有效筛选真实故障信息的正则门方法，使得RUL预测较为精确，寿命预测结果为79，而真实使用寿命大概是80。 文献[20-21]分别在第1 520 周期和1 675 周期时刻检测出系统的故障信息，本文方法在第1 770 采样周期内检测出系统异常并发出危险警报。

表2 不同算法中的预测寿命有效性对比

相对于没有添加在线监测模块的ISU-LSTM 网络，筛选掉噪声信息的作用不仅可以降低神经网络的训练时间，而且剔除假阳性故障F(Si，t)对于真实故障的影响。 实验结果显示在线监测模块的添加将训练时间缩短近5 s，故障检测精度提高3.5%。

为了验证本文网络算法的传感器故障预测性能，实验结果选用预测准确性和误检率来分别作为预测算法的优劣指标。 PF、IF、CF 分别代表永久故障、瞬态故障和间歇故障，本文通过不同算法在不同故障类型的检测精度和误检精度上进行比较。

图6 和图7 中显示，本文有效解决算法处理大数据存在的梯度下降问题，三个故障预测类型的精度都能稳定在95%以上，相对于其他算法有较大的提升。 误检率的实验结果显示数据在瞬态故障发生时的区分度较低，预测误检率较高。

图6 不同故障的预测准确率度对比

图7 不同故障的预测误检率对比

本文算法考虑到假阳性故障带来的影响，加入ISU 单元过滤掉传感器噪声信息，降低误报率。 实验结果关注对传感器假阳性故障误检为真实故障的误检率。 从图8 中可以看出，本文算法误检率可以降到10%以下，相对于其他算法，能较精确的检测出假阳性故障的发生，并将其筛选出来。

图8 假阳性故障预测精度对比

故障预测的准确性还需要将预期样本的数量与实际样本总数量的比例系数来判断预测模型的优劣。 式(19)中MSE 表示均方根误差系数，指标Kappa 表示预测识别率，用式(21)表示:

式中:po表示整体样本的预测精度，pe表示预测样本和真实样本一致的概率。k的大小衡量了模型预测的一致性。 针对参数指标MSE 的评价指标，本文添加参数调整优化模型的方法，通过迭代不断的缩小MSE 值，与传统神经网络和有添加在线监测模块的ISU-LSTM 算法相比，MSE 参数迭代的误差更小，检验的预测一致性系数Kappa 更高。

表3 不同算法中的误差系数对比

图9、图10 分别是不同算法的故障预测指标趋势曲线图，根据对MSE 和RUL 的趋势图发现本文算法相对于其他算法的优越性。

图9 不同算法的MSE 对比

图10 不同算法的RUL 对比

根据实验结果分析得到没有添加检测模型的ISU-LSTM 算法虽然在预测RUL 准确性上与本文算法没有太大差别，但由于没有参数调整优化的过程，与添加了在线模型存在较大的差距，本文算法得到的剩余使用寿命的预测趋势曲线更逼近于真实值。

4 结语

本文受到快速网络的启发，改进LSTM 中遗忘门结构，设计了一种含有内置稀疏单元的ISU-LSTM网络模型。 一方面，网络引入了双门控内置稀疏单元，改变了传统遗忘门结构接纳无用信息的劣势，最大化剔除假阳性故障影响；另一方面，采用实时监测故障模块能有效在线监测系统运作中可能存在的故障隐患，保证故障预测的实时性要求。 针对工业传感系统对故障预测实时性的巨大需求，ISU-LSTM 算法摒弃传统LSTM 繁琐的训练模式，加入稀疏优化单元，极大提高网络的训练速度，在多传感CPS 系统的故障预测领域取得较好的预测结果。