三相不控整流电路的谐波模型及容性电路等值特性分析
2021-05-15张岩王华佳张高峰王庆玉马硕庄静茹
张岩,王华佳,张高峰,王庆玉,马硕,庄静茹
1. 国网山东省电力有限公司 电力科学研究院,山东 济南 250000
2. 山东大学 电气工程学院,山东 济南 250061
近年来,随着分布式电源和多元负荷的接入,电力电子技术的发展使电网的运行与控制趋于复杂多样,大量采用三相不控整流电路的用电设备在工业生产和日常生活中获得了广泛应用[1-3],其广泛且随机分布在配电系统中,具有较高的谐波畸变,影响电力系统的电能质量,已经成为引起普遍关注的谐波源[4-5]。分布式谐波源的特性、各谐波源之间以及谐波源与系统参数之间的相互作用,会直接影响低压配电系统谐波水平的正确估计[6-7]。为减少三相桥式不控整流电路与系统阻抗发生谐振的可能,保证电网供电质量,需分析三相桥式不可控整流电路的谐波等值特性[8-9]。
目前,针对桥式不控整流电路的谐波模型已有一定研究。文献[10]研究单相电力电子负载的集合性谐波特性认为谐波水平与电压谐波畸变率成反比;文献[11]提出分析单相二极管桥式整流器谐波电流的时域方法;文献[12]指出低压配电系统非线性负荷的谐波衰减情况与电压的波形畸变程度有关。部分文献研究了三相桥式整流电路的参数取值和谐波特性,如文献[13]从功率角度分析了电压型三相桥式整流电路的运行机理,提出一种整流滤波电容值的迭代计算方法,证明在同等电压纹波下,该最小电容取值与后级所需功率成正比;文献[14]研究了三相可控整流电路的谐波产生机理及直流侧电流连续和断续的判定条件。三相不控桥式整流电路的对外等值容性特性会随着电路参数的不同而发生变化,此特性将影响到电路是否会与系统阻抗发生谐振,因此需要研究不同参数组合下的三相不控整流电路的对外等值谐波特性。
本文研究了带电容滤波的三相不控整流电路在直流电流断续条件下的频域谐波模型,推导出整流器等效电路阻抗的解析表达式。在此基础上,阐述了畸变电压条件下电路容性特性的机理,并提出给定电压条件下使三相桥式整流电路电容特性的电路参数范围确定方法,为有效分析电路与系统电感之间可能产生的谐振奠定理论基础。
1 三相桥式整流电路的频域谐波耦合导纳矩阵模型
在电容滤波的三相不可控整流电路中,最常用的即为三相桥式结构,图1 为其电路模型。图中C为负载侧滤波电容,R为负载等值电阻,Ia为交流侧电流,Id为整流输出侧直流电流,IC和IR分别为流经电容C和电阻R的电流,Ud为整流输出侧直流电压,VD1~VD6为晶闸管。
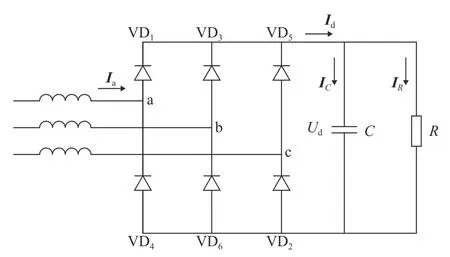
图1 电容滤波的三相桥式不可控整流电路
三相电压源换流器的供电电压中一般含有谐波成分,在三相电压平衡条件下,含谐波的电压源换流器(voltage source converter, VSC)供电端相电压可表示为[7]
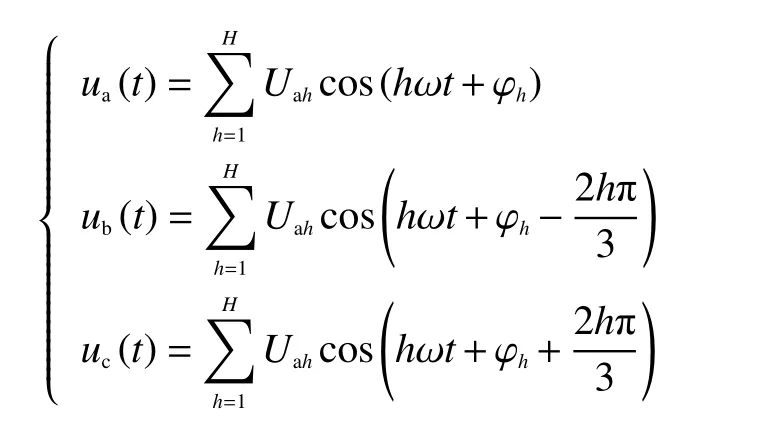
式中:h为谐波电压次数;H为所考虑到的最高阶谐波电压次数;Uah为A 相h次谐波电压幅值; ω为基波角频率,且 ω=2πf,f=50 Hz; φh为h次谐波的电压相位。
VSC 的线电压uab(t)和uac(t)可表示为[7]
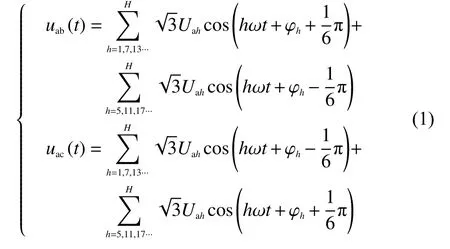
根据负载情况的不同,直流侧的电流可为连续或者断续状态。对于图1 所示的直流侧不含电感L的桥式不可控整流电路,断续时电流Ia波形如图2 所示,其中α和β分别表示不可控整流电路的开通角和截止角,Ia,m表示电流Ia的幅值。

图2 三相桥式不可控整流电路断续状态电流波形
由于直流侧电容的存在,电路在充电和放电2 种状态下交替运行。基于对电路关系分析可知,在不同的充放电阶段,交流侧电流ia为
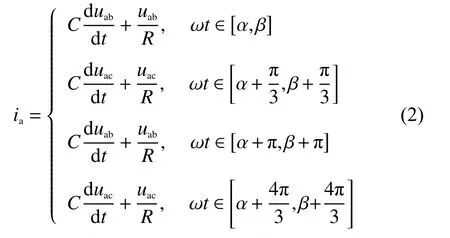
将式(1)代入式(2)进行计算,可求出在各导通区间内,交流侧电流ia(t)。
当α ≤ωt≤β 或α+π ≤ωt≤β+π时:


2 畸变电压下三相整流电路的容性机理分析
2.1 三相桥式整流电路在畸变电压下的等值电路
在三相桥式整流滤波电路中,当输入端电压含谐波时,A 相电压ua(t)及k次谐波电流Iak可分别表示为

三相桥式整流电路在畸变电压下的k次谐波等效电路如图3 所示。其中:R1=R/cosN,R2=-1/(kωC·sinN),C1=-CcosN,C2=-sinN/(kωR)。

图3 畸变电压下三相桥式整流电路k 次谐波等值电路
结合式(11)和图3 所示电路可得,在畸变电压条件下,k次谐波电压不能直接影响Ias,k,但是k次谐波电压会影响导通角、截止角的改变,从而对Ias,k的值仍有间接的影响作用。
2.2 畸变电压下电路容性特性机理分析
由前述分析可知,畸变电压下的k次谐波电流关系满足I1=Ik1+Ik2+Ias,k,而由于滤波电容的作用,Ik1+Ik2表现为容性电流。当Ias,k为容性时,k次谐波电流表现为容性;当Ias,k为感性,且其对等值电路所产生的影响大于等值导纳的影响时,电路即表现为感性。由于Ias,k受到电路基波电压、非k次谐波电压、滤波电容C、等值电阻R以及 α和β等参量的共同影响,因此可通过分别改变Ias,k的k次谐波电压的相位和幅值(直接控制量)、h(h≠k)次谐波电压的幅值和相位(间接控制量),来研究电路对外表现特性的变化规律。
以Ias,5和Ias,7为例,令滤波电容C=500 μF,负载等值电阻R=200 Ω,电源电压为基波、5 次谐波和7 次谐波的叠加。假设A 相的供电电压表示为

分析结果如图4 所示,Ias,5和Ias,7的相位会随着各次谐波电压相位的变化而出现明显变化,但Ias,5和Ias,7的幅值却受各次谐波电压幅值变化的影响较小。
从图4(a)、(b)可以看出,在5 次谐波电压相位变化时,Ias,7的相位变化要比Ias,5更加明显;而从图4(c)、(d)中可以看出,7 次谐波电压相位变化时,Ias,5的相位变化却比Ias,7更明显。此结果可进一步证明,k次谐波电压相位的变化不会直接影响Ias,k,因此当电路参数确定后,Ias,k只会在较小范围内波动。由上述分析可得,k次谐波等值电路中的等效电流源可以看作是一个不受交流侧k次谐波电压影响的基本恒定的电流源。

图4 谐波电压对谐波控制电流相角的影响
2.3 算例分析
根据图3 所示畸变电压下的k次谐波等效电路,以5 次谐波为例进行分析计算。已知导通角α及截止角 β的表达式如下(α ≤ωt≤β)。
1)截止角 β求解公式:

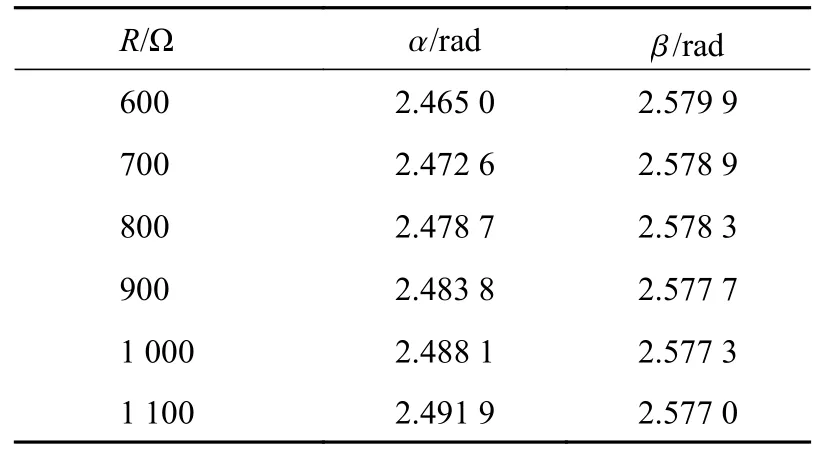
表1 算例1 条件下导通角及截止角的计算结果
将表1 中的数据分别代入式(8)~(11)中,求得当k=5 时,上述条件下的I51、I52、I51+I52、Ias,5和5 次谐波电流I5的5 组数据见表2。在此算例中,谐波电压相位为210°,则相位落后于210°的电流全部呈感性,相位超前于210°的电流全部呈容性,对表2 中的容性相位数值加粗显示。

表2 算例1 条件下各电流计算结果
当改变负载等值电阻R时,I51相对于5 次谐波电压全部表现为容性,且相位分布集中在-60.1°。而I52相对于5 次谐波电压全部表现为感性,但由于I52的幅值与I51相 比较小,所以I51+I52仍全部为容性。Ias,5包含容性或感性2 种特性,进而使I52 种特性均有表现。
对表2 中I5的相位进行分析,当电阻R为800 Ω时,I5的相位为-150°,表现为容性特性;且当电阻小于800 Ω 时,I5的相位均大于-150°,表现为容性;而当电阻大于900 Ω 时,I5的相位均小于-150°,表现为感性。从而可以看出,电路表现为容性还是感性的分界点在电阻R介于800 ~900 Ω的某个值,因此在给定电压条件下,电路表现为容性或感性的分界点可由电阻R处于某个值为界。
3 三相桥式整流滤波电路容性特性下的等值电阻计算
在确定电源电压条件下,三相桥式整流滤波电路对外表现为容性或感性是由滤波电容C与等值电阻R的大小共同确定,而负载在给定电压条件下的滤波电容和等值电阻是可求的。因此可求出在电压及滤波电容C给定时,使谐波电路表现为容性特性的负载等值电阻R的范围,步骤如下:
1)确定电路在负荷侧的电压条件以及负载电容。
2)在步骤1)条件下,计算无穷大电阻对应的截止角,记为 β0,设置截止角 β的取值范围为[β0,π/2]。
3)将电压条件及截止角 β的值代入式(12),求解对应的ωRC。
4)将步骤3)中求出的ωRC值代入导通角 α的求解公式(13)中,使用牛顿迭代法,计算求解 α。
5)将上述步骤中所求得的 α、 β及ωRC值分别代入式(11)的k次谐波电流公式,求解使k次谐波电流超前于k次谐波电压的截止角范围,再次代入式(12),进一步求取ωRC范围。
6)确定滤波电流C的取值,求取能够使k次谐波电路表现为容性特性的R取值范围。
算例2设置电路参数为ua(t)=Ua1cos(ωt)+Ua5·cos(5ωt-120°),以Ua5=3%Ua1,φ5=-120°,C=500 μF为例,根据上述步骤进行计算,即可求得使电路呈容性的R取值范围。其中,β0=2.45,图5 即为负载等值电阻R、 5 次谐波的电流电压相位差Δφ5分别与截止角 β的变化关系。由图5 可知,负载等值电阻R与截止角 β成反比。但是随着截止角的增大,5 次谐波电流与5 次谐波电压的相位差由正变负,电流由滞后变为超前,即三相桥式整流电路对外表现特性从感性变为容性。
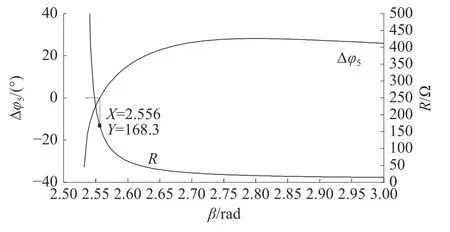
图5 R、Δφ5与β 的变化关系
在上述算例中,当R=168.3 Ω时,5 次谐波电流电压的相位差为0;当R>168.3 Ω 时,Δφ5小于0°,即5 次谐波电路表现为感性,电路在5 次谐波处不存在发生谐波谐振的可能性;当R<168.3 Ω,此时 Δφ5大于0°,电路在5 次谐波处呈容性。同理可得其他次数谐波情况下的分析结果。
4 结论
本文针对直流侧带电容滤波的三相不控桥式整流电路在当直流电流断续时会产生大量谐波电流这一问题,推导了三相桥式不可控整流电容滤波电路的谐波耦合导纳矩阵模型。通过算例仿真,验证了所提出方法的准确性。
1)建立了电容滤波三相不控整流电路在直流电流断续条件下的频域谐波耦合导纳矩阵模型,可更直观地体现整流器谐波电压与谐波电流之间的耦合关系。
2)在频域谐波模型基础上分析了三相桥式整流电容滤波电路在畸变电压条件下的谐波等值特性,研究了不同电压及负载参数下电路对外特性的变化规律。
3)研究了能使电路在一定电压条件下表现为容性的电路参数范围,所提出的分析方法和研究结论可为三相整流电路的谐振分析奠定基础。
