利用Ricker子波相移特性估计地震资料剩余相位

刘传奇 周建科 李 宾 王 腾

(中海石油(中国)有限公司天津分公司，天津 300459)

0 引言

众所周知，零相位地震子波具有旁瓣少、峰值时刻与地层反射界面相对应等优点，能保证零相位地震资料不仅具有较高分辨率，还有利于地震资料的解释[1-9]。确保地震资料的零相位性，无疑对构造精细解释、储层综合研究具有重要意义。在现今实际地震数据处理中，一般基于地震子波为最小相位的假设，从地震道的相位谱中消去子波的相位谱。然而从现场采集到室内处理的各个环节，均可能对地震数据的子波相位特性产生影响，因此最小相位子波的假设条件通常是很难满足的，混合相位假设的子波更符合实情。虽然混合相位地震子波假设能在某些特定条件下取得一定效果，但基于此假设的一些算法在计算量、实用性以及稳定性等方面大多还存在不足。因此，实际地震数据处理中仍大多基于最小相位假设制订处理流程。混合相位子波经最小相位反褶积处理后必然存在剩余相位，即并不是真正的零相位，尚需通过其他技术手段估算出剩余相位并进行校正处理[10-14]。

若认为地震子波相位谱不随频率发生变化，可采用常相位扫描法进行剩余相位估计，该类方法处理结果的好坏很大程度上取决于判别准则的选取。Levy等[15]提出采用最大方差模准则估算剩余相位，有效提高地震剖面的解释能力； 但最大方差模准则也存在诸如计算效率低、对弱反射信息不灵敏、不能反映尖脉冲的极性和时移等不足。Sacchi等[16]、Lu 等[17]分别对最大方差模准则进行局部改进，减弱传统最大方差模准则对较强反射信息的敏感性。针对最大方差模准则对噪声的不敏感性，Ooe等[18]提出指数变换准则，调节噪声压制与恢复小反射系数序列之间的平衡。Claerbout[19]提出的Parsimony准则用降低幂次的方法削弱强反射信息的作用，对强、弱反射信息都有较高灵敏度。单联瑜等[20]改进了常用相位校正判别准则，提出一种新的相位校正方法，实现精确的相位校正。徐刚等[4]通过以离散信息熵作为量化标准，对无井地震记录进行相位扫描，进而求取剩余相位。Fomel 等[21]、刘俊州等[22]使用偏斜度准则实现子波剩余相位的估计。此外，在具有可靠的测井数据情况下，可采用零相位子波制作合成记录，并将其当作标准道，用相似系数作为判别准则[23-24]。

本文通过研究Ricker子波的相移特性，发现主频不同的Ricker子波在相同相位旋转下，峰值时刻存在时差，且该时差与相位旋转量具有线性关系。在常相位假设下，通过该线性关系可实现地震资料剩余相位的估计。该方法不需判别准则的约束，具有精度高、实现过程简捷等优点。

1 方法原理

分别对主频为20、35、50及65Hz的零相位Ricker子波进行相位旋转，旋转角度依次为15°、30°、45°、60°、75°及90°，得到图1所示结果。可见不同主频零相位Ricker子波波峰位置始终位于零时刻处； 随着相位旋转，波峰逐渐偏离零时刻。表1统计不同主频Ricker子波相位旋转量与波峰时移量的关系，可见波峰时移量与主频及相位旋转量有关： ①同一主频Ricker子波随相位旋转量的增加其波峰时移量也增加； ②在相同相位旋转量下，主频越高波峰时移量越小。换而言之，Ricker子波相位与主频、峰值时刻有关，若能定量求出三者的关系，就可通过主频和峰值时刻求取相应相位值。

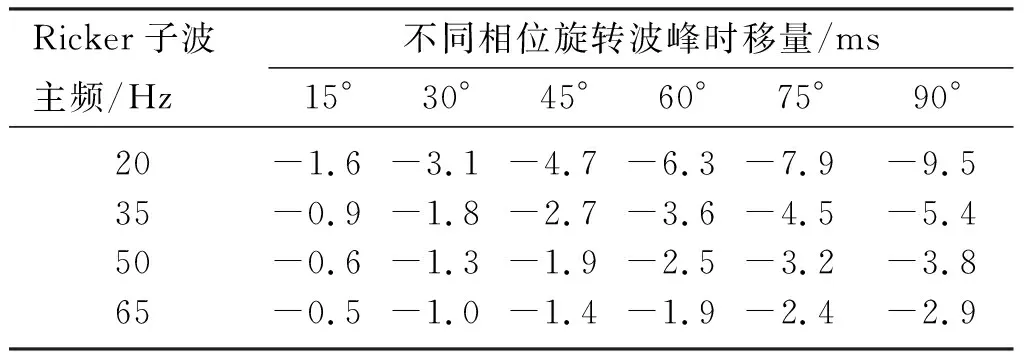
表1 Ricker子波在不同相位旋转下的波峰时移量

主频不同的Ricker子波在相同相位角旋转量下，其峰值时刻存在差异，可尝试通过峰值时刻的差异求取相位旋转量。以主频为20Hz和60Hz的Ricker子波为例。首先将其进行相位旋转(图2)，然后求取相同相位角下的峰值时差，将峰值时差与相位旋转量进行拟合，结果表明峰值时差与相位旋转量存在线性关系(图3)。改变Ricker子波主频，峰值时差与相位旋转量仍然存在线性关系，只是比例系数不同而已，主频差异越大，比例系数越小(图4)。此分析结果表明，利用Ricker子波的主频和峰值时差求取相位旋转量是可行的。

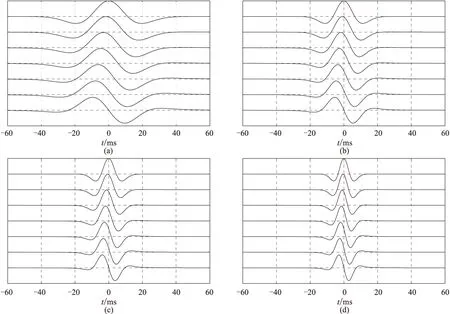
图1 不同主频Ricker子波随相位角旋转的变化

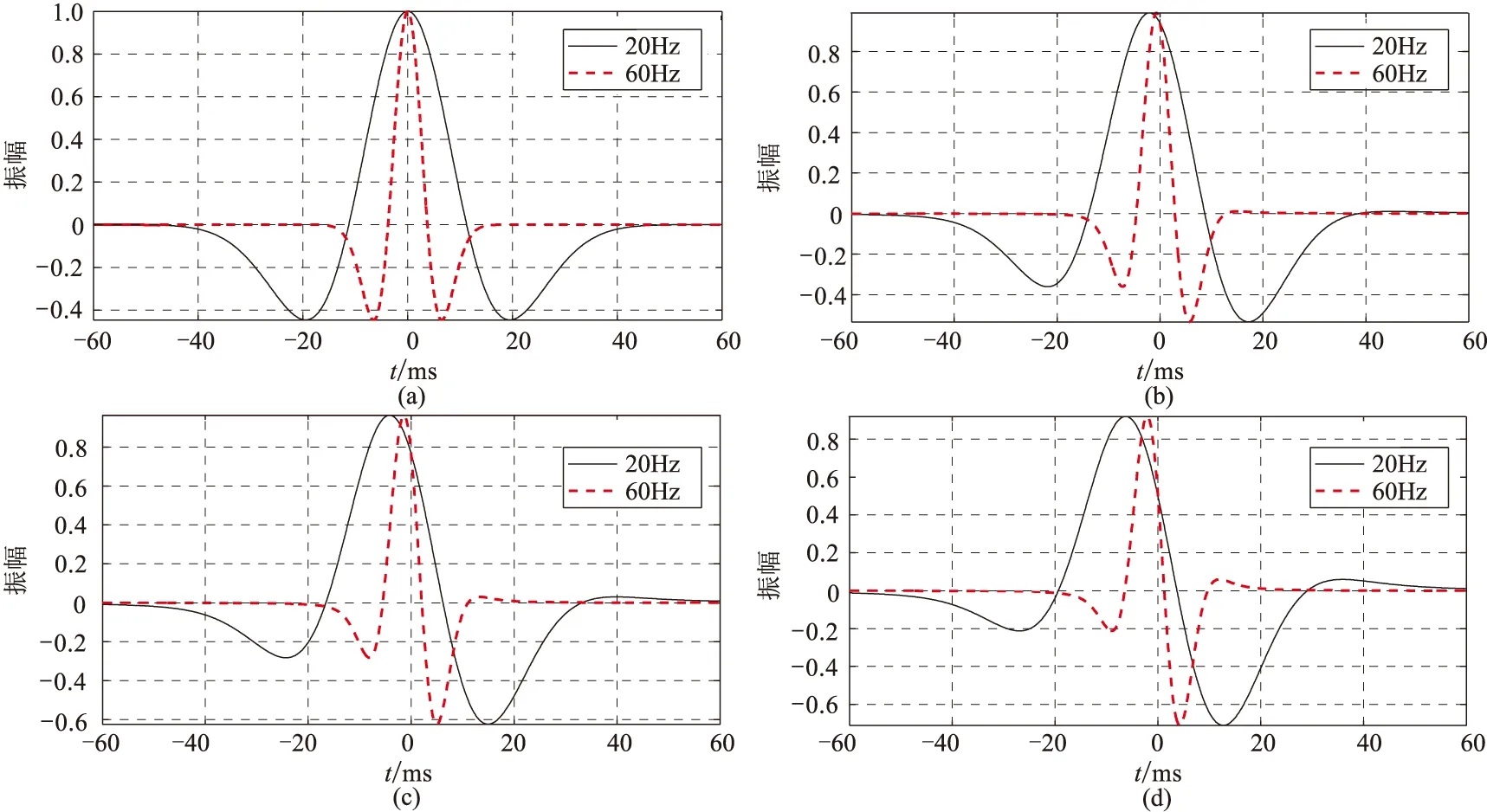
图2 主频为20Hz和60Hz的Ricker子波在不同相位旋转量的波形对比

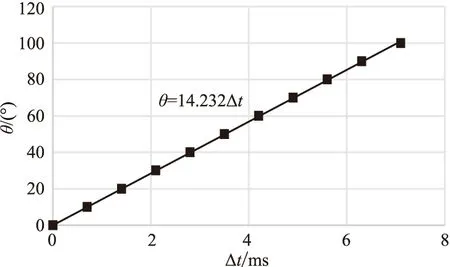
图3 主频为20Hz和60Hz的Ricker子波峰值时差Δt与相位旋转量θ的关系

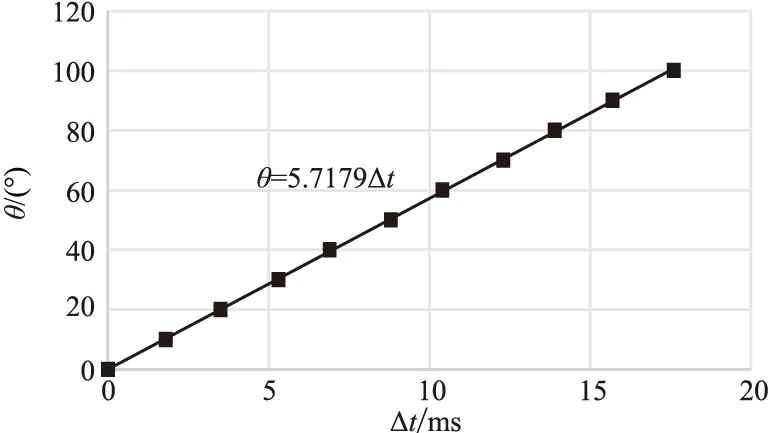
图4 主频为10Hz和60Hz的Ricker子波峰值时差Δt与相位旋转量θ的关系

基于以上研究结果，本文提出一种新的剩余相位估计方法： ①首先对相位未知的地震数据进行频谱分析，确定出有效频带； ②在有效频带的低频和高频两个区域分别选取相应滤波主频，滤波因子为Ricker子波，得到低通和高通两个数据； ③对低通和高通数据做频谱分析，确定各自主频，记为f1和f2； ④求出Ricker子波主频分别为f1和f2时峰值时差与相位旋转量的关系； ⑤求出同一反射界面在低通和高通数据上的峰值时差； ⑥将⑤中峰值时差代入④中的线性关系，得到地震数据剩余相位。

为提高剩余相位估计精度，需注意以下两点：①在有效频带范围内，两次滤波所选主频差异尽可能大； ②为减小求峰值时差的偶然误差，在实际应用中需用多道求取峰值时差，然后取其平均作为最终的峰值时差。

2 理论模型试算

对主频为35Hz，相位角为0°、30°、60°的Ricker子波做滤波处理，滤波主频分别为15Hz和60Hz，得到图5所示结果。对滤波后数据进行频谱分析(图6)，主频为35Hz的Ricker子波经过主频为15Hz和60Hz的Ricker子波滤波处理后，主频分别变为20Hz和43Hz。经过统计分析，峰值时差与相位旋转量的拟合关系式为θ=17.064Δt(图7)。

从图5中可见，当相位角为0°时，峰值时差为0，由拟合关系得出的相位角为0°； 当相位角为30°时，峰值时差为1.7ms，由拟合关系得出的相位角为29.0°，与实际相位值仅差1.0°； 当相位角为60°时，峰值时差为3.5ms，由拟合关系得出的相位角为59.7°，与实际相位值基本一致。

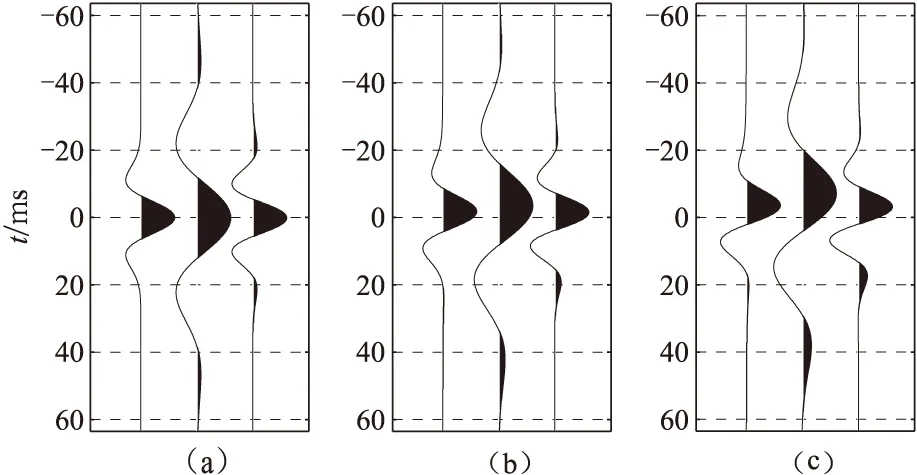
图5 主频为35Hz、相位角依次为0°(a)、30°(b)、60°(c)的Ricker子波滤波后峰值时刻的变化滤波主频分别为15Hz(中)和60Hz(右)

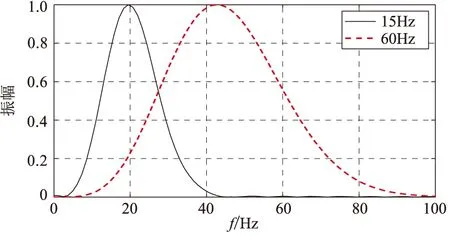
图6 主频为35Hz的Ricker子波经过主频分别为15Hz和60Hz的Ricker子波滤波后的频谱

采用反射系数序列(图8a)与35Hz主频、40°相位Ricker子波进行褶积运算，得到合成地震记录(图8b)，分别采用主频为15Hz和60Hz的Ricker子波对其做滤波处理(图8c、图8d)。为避免干涉效应的影响，选取300ms处的波峰计算峰值时差，对300ms附近滤波后数据进行放大(图8e)，可见15Hz滤波结果峰值时间为295.6ms、60Hz滤波结果峰值时间为298.1ms，对应峰值时差Δt=2.5ms。将该峰值时差代入图7中关系式，计算出剩余相位为42.6°。采用该剩余相位角对原始记录进行零相位校正，所得结果(图9a)与主频相同的零相位Ricker子波合成记录(图9b)相一致。

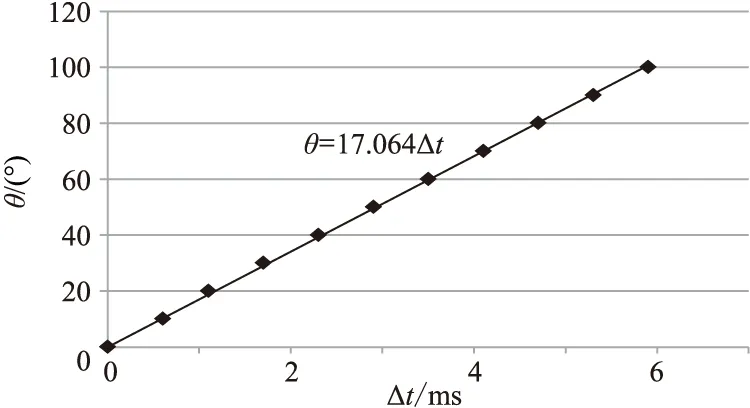
图7 主频为20Hz和43Hz的Ricker子波峰值时差Δt与相位旋转量θ的关系

为进一步验证本文方法的适用性，用带通子波(图10)替换上述的Ricker子波。将该带通子波分别进行30°、60°相位角旋转，采用主频分别为16Hz和43Hz的Ricker子波进行滤波处理，得到如图11所示结果。对滤波后的数据进行频谱分析(图12)，该带通子波经过主频为16Hz和43Hz的Ricker子波滤波处理后，主频变为20Hz和43Hz，因此峰值时差与相位旋转量的拟合关系式为：θ=17.064Δt(图7)。从图11中可看出： 当相位角为0°时，峰值时差为0，由拟合关系得出的相位角为0°； 当相位角为30°时，峰值时差为1.8ms，拟合得出的相位角为30.7°； 当相位角为60°时，峰值时差为3.6ms，拟合得出的相位角为61.4°。

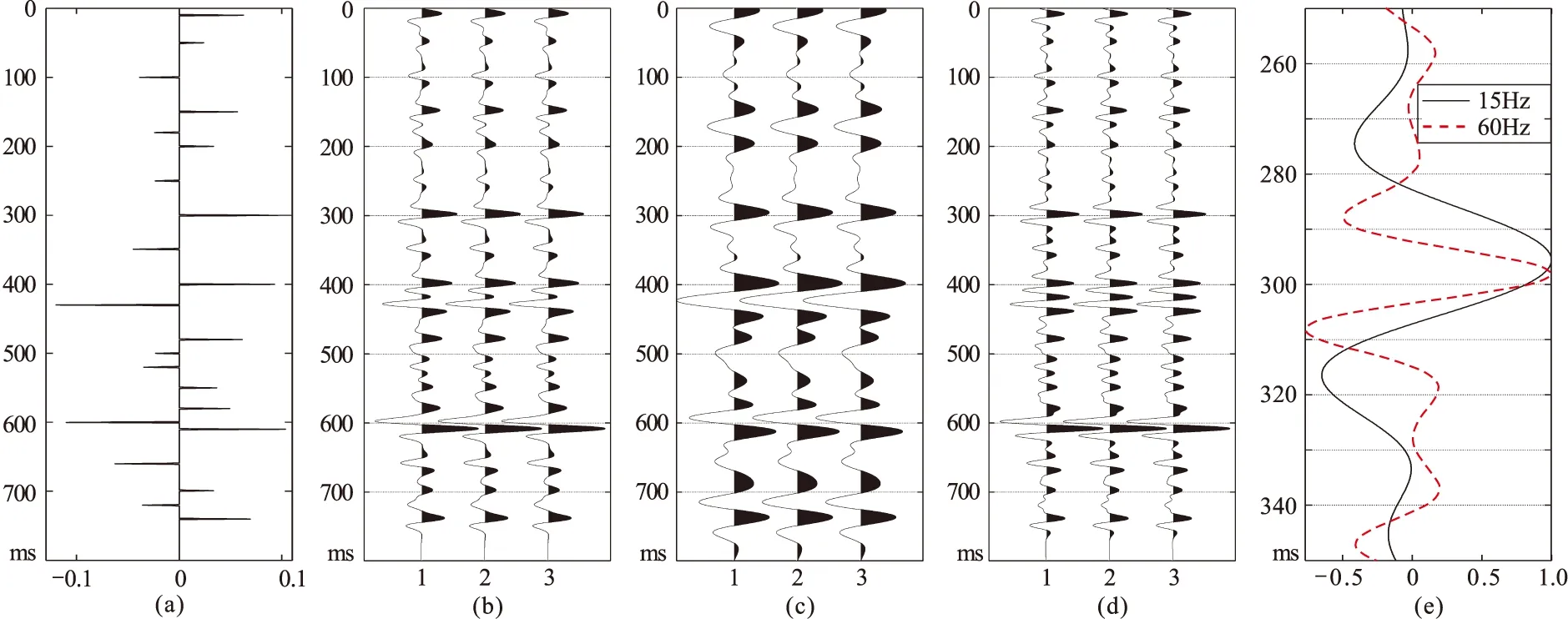
图8 反射系数、40°相位角Ricker子波合成地震记录及滤波结果

采用图8a的反射系数与40°相位角的带通子波进行模拟，得到图13a所示的合成地震记录； 分别用主频为16Hz和43Hz的Ricker子波对其做滤波处理(图13b、图13c)。对300ms附近滤波后数据进行放大显示(图13d)，16Hz滤波结果的峰值时间为295.5ms，43Hz滤波结果的峰值时间为297.8ms，对应峰值时差Δt=2.3ms，将该峰值时差代入图7中关系式，计算出剩余相位角为39.2°，较准确地估计出地震记录的剩余相位角。可见本文方法对带通子波也具有较强适用性。

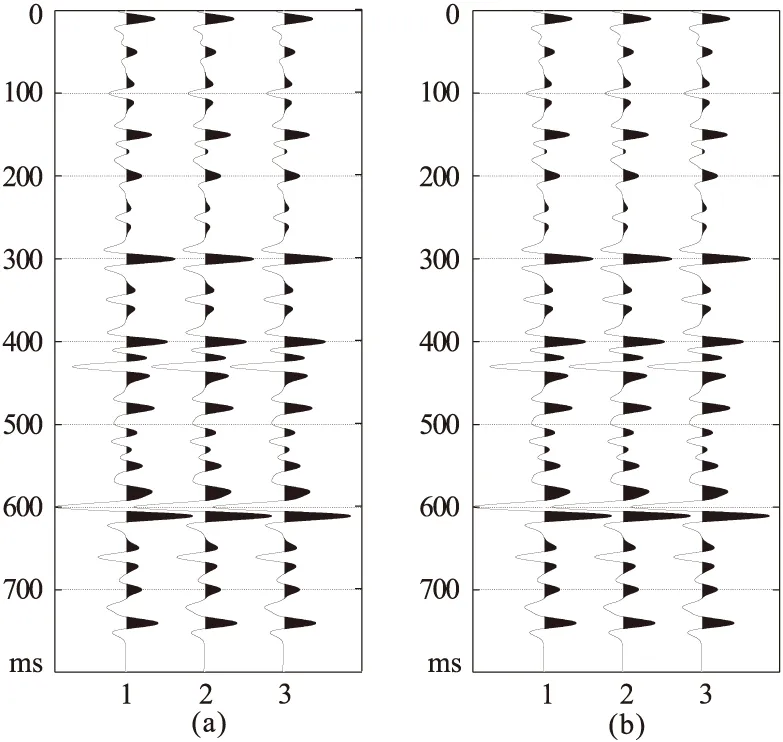
图9 基于本文方法零相位化处理结果(a)及零相位Ricker子波合成记录(b)

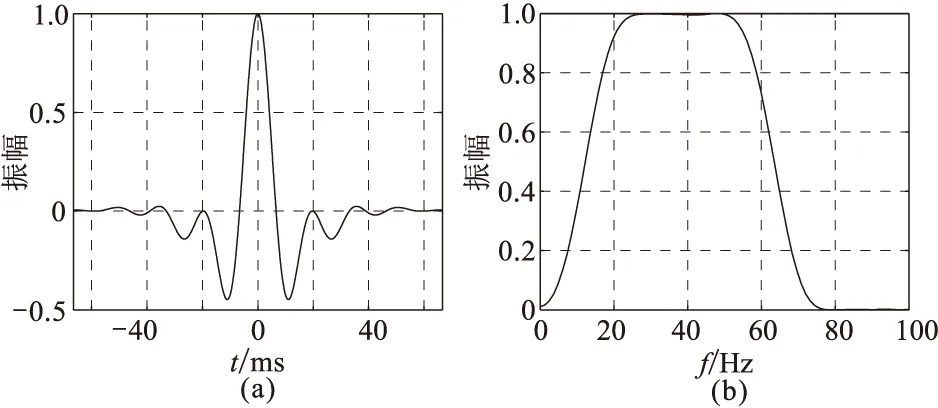
图10 带通子波(a)及其频谱(b)

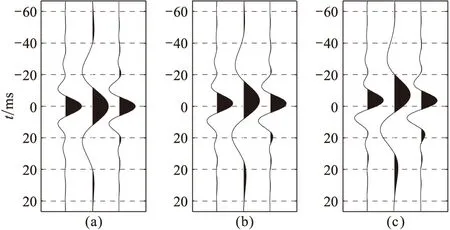
图11 相位角依次为0°(a)、30°(b)、60°(c)的带通子波滤波后峰值时刻的变化滤波主频分别为16Hz(中)和43Hz(右)

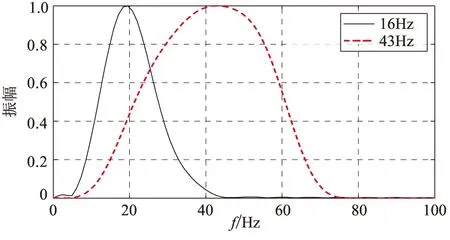
图12 带通子波分别经过主频为16Hz和43Hz的Ricker子波滤波后的频谱

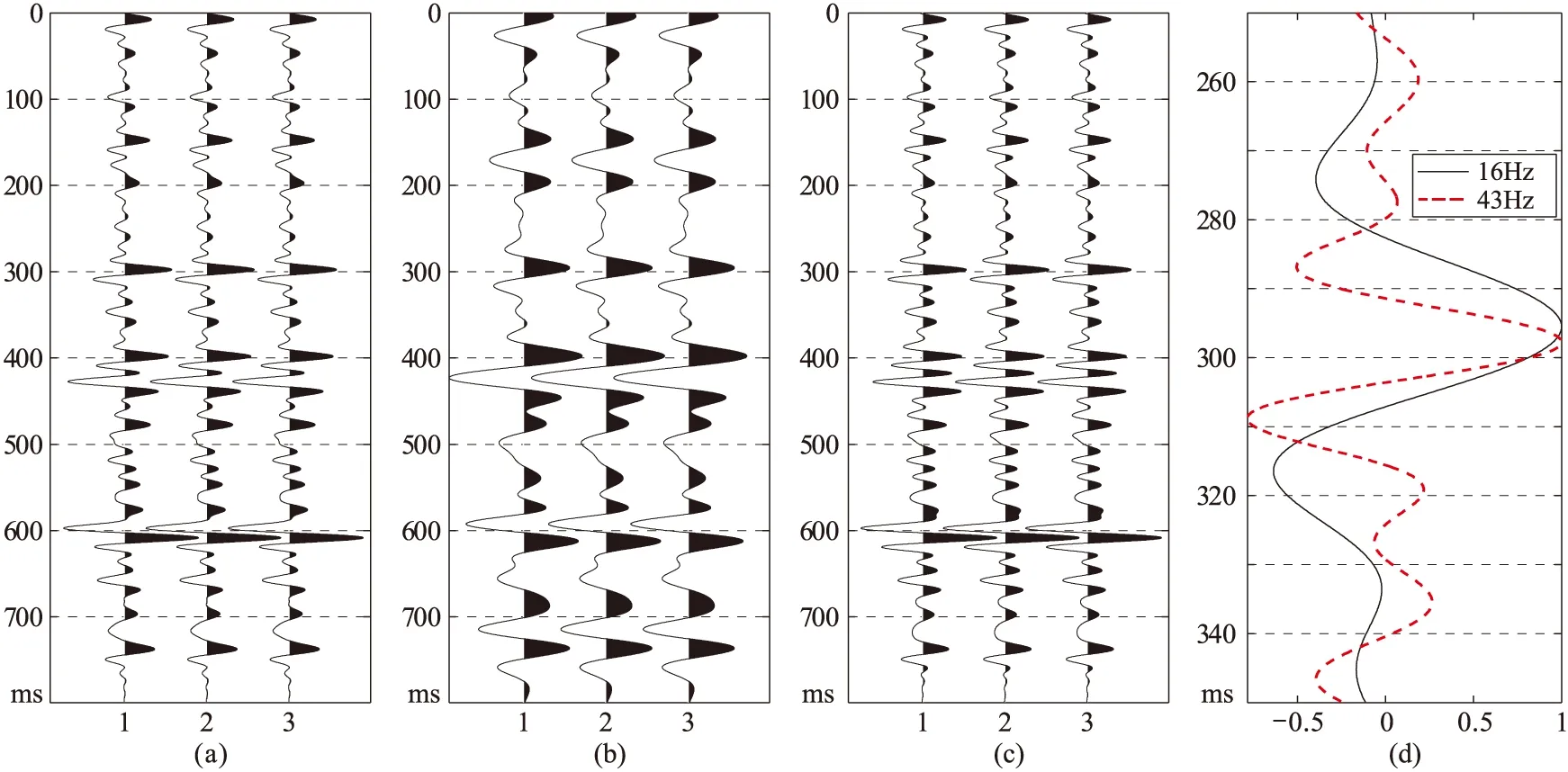
图13 40°相位角带通子波合成地震记录及滤波结果

3 实际数据应用

图14a为渤海M区实际叠后地震剖面，采用本文方法对其进行剩余相位估计并做零相位化处理，得到图14b所示结果。可见经零相位化处理后剖面上弱反射同相轴能量得到增强，分辨率有一定改善(黑色箭头所指)。

为验证本文方法的可靠性，运用本文方法求得该实际地震资料的剩余相位角是40°。 为更好地研究储层的发育特征，对该资料做-40°相移后再进行反演(图15)。原始地震资料反演结果认为目的层处A15井与A16井不连通(黑色箭头所指)，而经相位校正后的资料反演结果认为目的层处A15井与A16井是连通的。油气开采动态资料表明，A15井注水后，A16井很快有反应，表明A15井与A16井之间的储层的确是连通的。这也证实基于本文方法得到的剩余相位角是可信的。

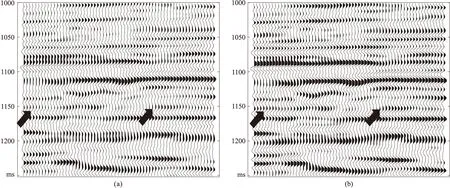
图14 实际地震资料基于本文方法零相位化处理前(a)、后(b)剖面对比

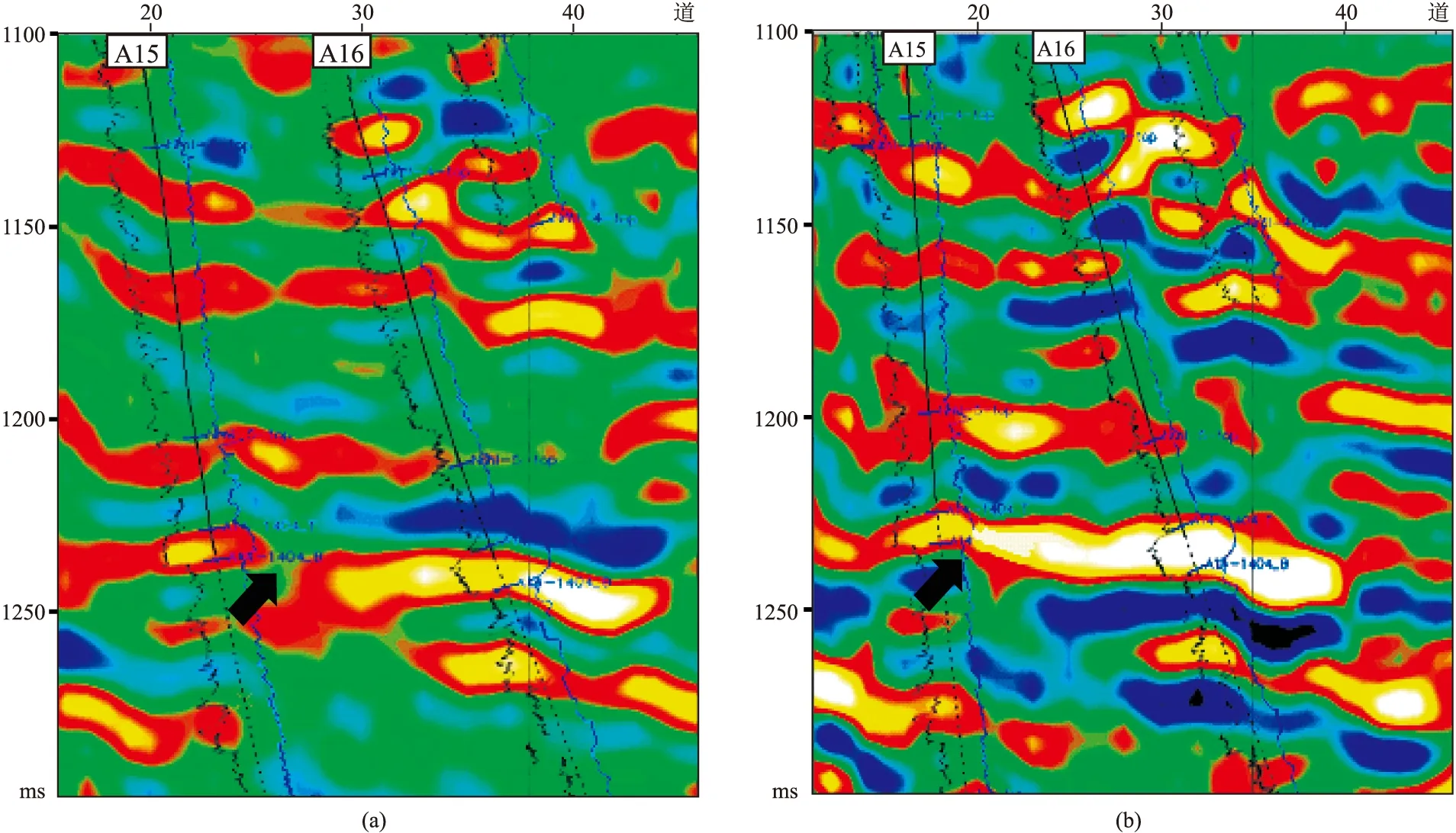
图15 基于本文方法零相位化处理前(a)、后(b)反演剖面对比

4 结束语

对地震数据剩余相位的估计，前人研究成果大多是建立在一定判别准则上进行的，判别准则选取的合理性，直接影响最终结果。本文通过研究Ricker子波的相移特性，发现主频不同的Ricker子波在相同相位旋转下，峰值时差与相位旋转量具有线性关系，通过该线性关系实现地震资料剩余相位角的估计。该方法不需要判别准则的约束，原理简单、运算量小、精度高，具有较强实用性。模型试算和实际资料处理结果表明，本文方法能有效地估计出地震数据的剩余相位角，从而实现地震资料的零相位化。