自适应稀疏反演多次波压制方法

杨旭明,王 丽,陶长江,鲍 伟

(中国石油化工股份有限公司江苏油田分公司物探研究院,江苏南京210046)

地震勘探中多次波问题普遍存在,多次波的存在使得一次反射波的相位、振幅和频率等动力学特征失真,对构造解释和地震反演都造成了不利影响。当一次波和多次波相互重叠时,会更加难以识别和处理多次波。因此,在地震资料处理中,有效压制多次波一直是地震处理研究的重点和难点之一。

BERKHOUT[1]提出了描述复杂多次波系统的反馈理论框架,奠定了反馈迭代多次波压制方法的数学物理基础,提出的多维反演算法通过数据矩阵相乘预测多次波,能够适应任意复杂的地下结构。但消除多次波时需要已知震源子波。VERSCHUUR[2]引入基于一次波能量最小假设的自适应相减方法,成功地从实际地震数据中估计出震源子波,极大地推动了表面相关多次波压制方法(surface-related multiple elimination,SRME)的发展。为了避免因求解震源子波而产生的非线性优化问题,VERSCHUUR等[3]提出了迭代SRME方法,在每次迭代过程中采用最小二乘匹配多次波模型与原始数据,确定震源子波,将原来的非线性问题转化为线性问题,增强了方法的实用性。为了避免自适应相减可能损伤有效信号,SRME被重新定义为反演一次波脉冲响应和震源子波的全波形反演问题,形成了基于稀疏反演的一次波估计方法(estimation of primaries by sparse inversion,EPSI)[4-5]。

传统的EPSI方法需要精确地包含有一次波的时窗和反演参数设定,存在一定的不稳定性。因此,需要对EPSI方法进行改进,将其转化成为双凸优化问题[6],即反演一次波脉冲响应过程中采用的目标函数是一个凸函数,应用的约束集合同样也是一个凸函数,通过交替优化迭代过程,对一次波脉冲响应采用谱梯度投影(SPGL1)[7]算法求解,同时引入帕累托优化(pareto)曲线。改进的EPSI方法[8-10]在求解过程中,需要在输入记录的多维互相关数据中拾取与最强反射一次波相一致的同相轴来估计初始的震源子波。该工作不仅费时费事,还可能由于识别错误和拾取参数设置误差,得不到合适的震源子波。冯飞[11]使用常规最小平方正交三角(QR)分解算法求解震源子波。宋家文等[12]和白兰淑等[13]通过匹配滤波方法求取地震子波。本文提出的自适应稀疏反演多次波压制方法(adaptive estimation of primaries by sparse inversion,AEPSI),不需要人工拾取和时窗设置,完全由数据驱动解决初始震源子波及震源子波迭代更新问题。

1 方法原理

1.1 自适应稀疏反演多次波压制原理

为了便于理解和推导,EPSI频率域方程表示为:

P=GQ+GRP

(1)

式中:P为频率域数据矩阵;G为频率域一次波脉冲响应;R为频率域自由表面反射算子;Q为频率域震源矩阵。如果用q(t)表示对应于时间域数据矩阵p的震源特性,并假定q(t)对所有的炮和道是不变的,则Q=w(ω)I。其中,w(ω)是频率的标量函数,是q(t)的频率域表示;I是单位矩阵。假定自由表面反射算子R=-I。方程通过逆傅里叶变换返回到时间域,G的时间域表示为g,P的时间域表示为p,时间域子波q(t)简记为q,则时间域数据矩阵p可表示为:

p=M(g,q;p)

(2)

由于稀疏约束是施加在时间域,所以用作用在时间域的M(g,q;p)函数讨论问题会更方便。如果基于数据矩阵p的方程(2)用隐式表示,则有:

p=M(g,q)

(3)

对于方程(3)来说,如果给定变量g、q中的一个,则M(g,q)变成了相对另一个变量的线性算子。因此,M(g,q)也叫做双线性算子,可以写成:

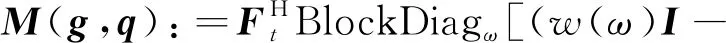
(4)

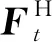
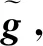
(5)

(6)

根据(5)式和(6)式,定义:

(7a)

(7b)

(8)

式中:q∈Λ表示满足任何所需的或先验约束施加在震源上。这里假定q在时间域是短时窗的震源子波,并允许非因果的描述记录数据中可能出现的时移。当然,也可以施加其它需要的震源特性。

根据迭代求解约束优化问题的方法,则可以通过下列两个子问题的迭代求解EPSI约束优化问题:

(9)

(10)

(11)

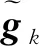
(12)

调整因子sk为:

(13)

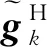
1.2 初始震源子波的确定

实际中的地震子波是一个很复杂的问题,因为地震子波与地层岩石性质有关,地层岩石性质本身就是一个复杂体。为了研究方便,对地震子波进行模拟,这就是理论子波。目前普遍认为Ricker提出的地震子波数学模型具有广泛的代表性,因此,Ricker子波可作为初始震源子波。Ricker子波公式如下:

(14)

式中:t为时间;A为振幅;fm为主频。图1展示了主频从15Hz到45Hz,振幅A为1.0的Ricker子波。

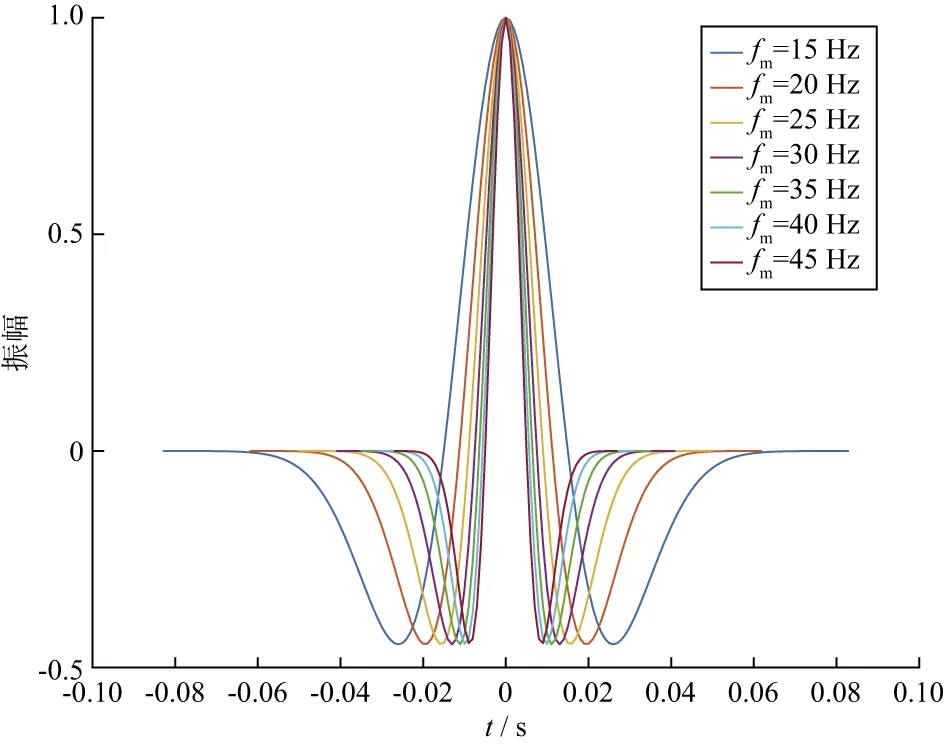
图1 不同主频Ricker子波

假定地震子波已知为q(t),且振幅A=1.0,由(4)式有:

M(g,q):=

=Mqg=Qqg+Pqg=p

(15)

这里定义算子:

(16)

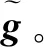
(17)

(18)

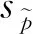
同理,要求多次波的估计值pm和一次波估计值pp,与实际地震记录p也在能量水平上接近,分别用sm和sp表示比例系数,则有:

(19)

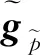
(20)

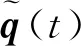
1.3 自适应逼近实际地震子波

通常在EPSI算法中,使用SPGL1方法求解,其中子波求解采用常规的最小平方QR分解算法或匹配滤波算法。这里采用无约束非线性优化算法。定义目标函数为:

(21)

则无约束非线性优化问题为:

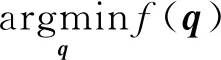
(22)

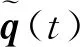
实现流程如下。

1) 输入地震记录p,设定残差值σ(‖p‖2的5%～10%)。

2) 根据地震记录的主频fm计算振幅A=1的Ricker子波q(t)。

5) 迭代计数k=0,L1范数约束τ0=0。

6) 循环开始。

7) 由σ和τk,通过SPGL1确定τk+1。

12)k=k+1。

2 应用算例

2.1 简单岩丘模型

设计一个如图2所示的顶部有水层的岩丘地质模型。该模型的水层深度在200m左右,横向变化的盐丘层大致位于深度400～800m。通过时间二阶、空间四阶有限差分声波程序进行正演模拟,使用主频为25Hz的零相位Ricker子波。震源线与接收线精确重合,道间距为15m。

图2 顶部有水层的简单岩丘模型

2.1.1. 应用效果测试分析

抽取排列在岩丘高点附近的150道数据进行处理。图3a是测线中部相邻两炮原始数据,水层底部和盐丘的顶部产生的一阶及高阶多次波(图中白色箭头指示处)严重影响了一次波同相轴。图3b是采用本文方法压制多次波后的对应单炮记录,图中白色箭头指示处的多次波已得到有效压制,一次波得到很好的恢复,1.6s以下空白,没有信息,这与模型1700m以下没有反射层相对应。图3c是采用EPSI方法压制多次波后的对应两炮记录,白色箭头处的多次波也得到压制。对比图3b和图3c可以看出,图3b中的绕射波更完整,同时最右边的箭头和最下边两个箭头处,原来被多次波掩盖的有效波得到更好的恢复,说明采用本文方法压制多次波时,有效波得到更好的保护和恢复。

图4a为原始数据的零炮检距剖面,多次波严重影响资料品质。图4a中存在两个产生较强多次波的界面,一个是水层顶面,一个是水层底面,图中白色箭头指示了表面相关一阶和高阶多次波。水层顶面产生表面相关多次波,水层底面产生层间多次波。图4b 为采用本文方法进行多次波压制后的零炮检距剖面,可以看出,白色箭头所指水层表面产生的各阶多次波得到大幅压制,被掩盖的一次波同相轴得到了很好的恢复,多次波压制效果良好。在0.8s左右存在由水底产生的层间多次波。在1.2s左右处,存在由水底产生的高阶层间多次波。对于这些层间多次波,可采用其它层间多次波压制方法进一步压制。图4c 为采用EPSI进行多次波压制后的零炮检距剖面。可以看出,图4c整体效果与图4b相当,但图4b中的绕射波信息更完整,同时最下面的两个白色箭头处的弱反射也完整地显现出来了。

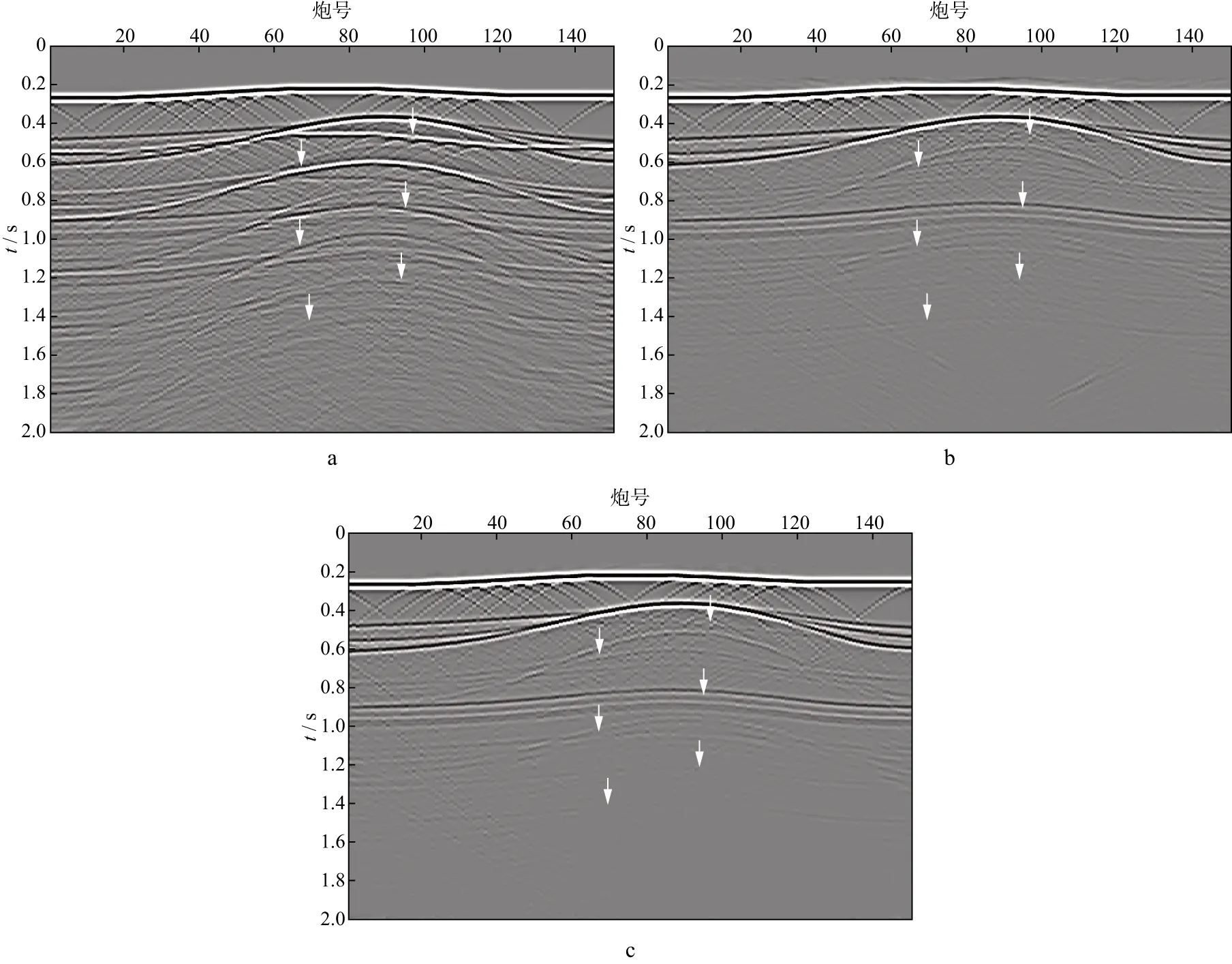
图4 采用不同方法进行多次波压制后的零炮检距剖面a 原始数据; b 本文方法;c EPSI

2.1.2 初始子波误差容忍度分析

为了分析本文方法对初始子波误差的容忍度,基于同样的数据集,分别采用主频为20Hz的零相位、最小相位和混合相位Ricker子波作为初始输入子波,应用本文方法进行处理和分析。

不同相位子波输入的多次波压制结果如图5所示。图5a为原始单炮记录(局部),含有严重的表面相关多次波,图中白色箭头指示了主要多次波。图5b 至图5d分别为零相位子波、最小相位子波和混合相位Ricker子波输入时的多次波压制结果。从图5 可以看出,表面相关多次波得到有效压制(如图中白色箭头所示),一次波得到较好恢复,不同相位子波输入对多次波压制效果影响较小,表明本文方法不受输入子波类型影响,对初始子波误差的容忍度较高。

不同相位子波输入时的子波迭代更新结果如图6 所示。图6a为零相位子波迭代更新结果,初始子波(k=1)经过4次迭代,子波的主频和振幅趋于稳定,并且向实际理论子波逼近。求取的子波(k=4)和模拟正演使用的理论子波(主频为25Hz的零相位Ricker子波)一致。图6b为最小相位子波迭代更新结果,初始子波(k=1)经过5次迭代,求取的子波(k=5)和模拟正演使用的理论子波一致。图6c为混合相位子波迭代更新结果,初始子波(k=1)经过5次迭代,求取的子波(k=5)和模拟正演使用的理论子波一致。

采用主频为20Hz的零相位、最小相位和混合相位Ricker子波作为初始输入子波,应用本文方法进行处理,最终子波都收敛到正演模拟数据的实际理论子波,而多次波压制效果没有明显变化,说明子波迭代更新结果受产生数据的实际子波控制,本文方法对子波误差具有较高的容忍度。

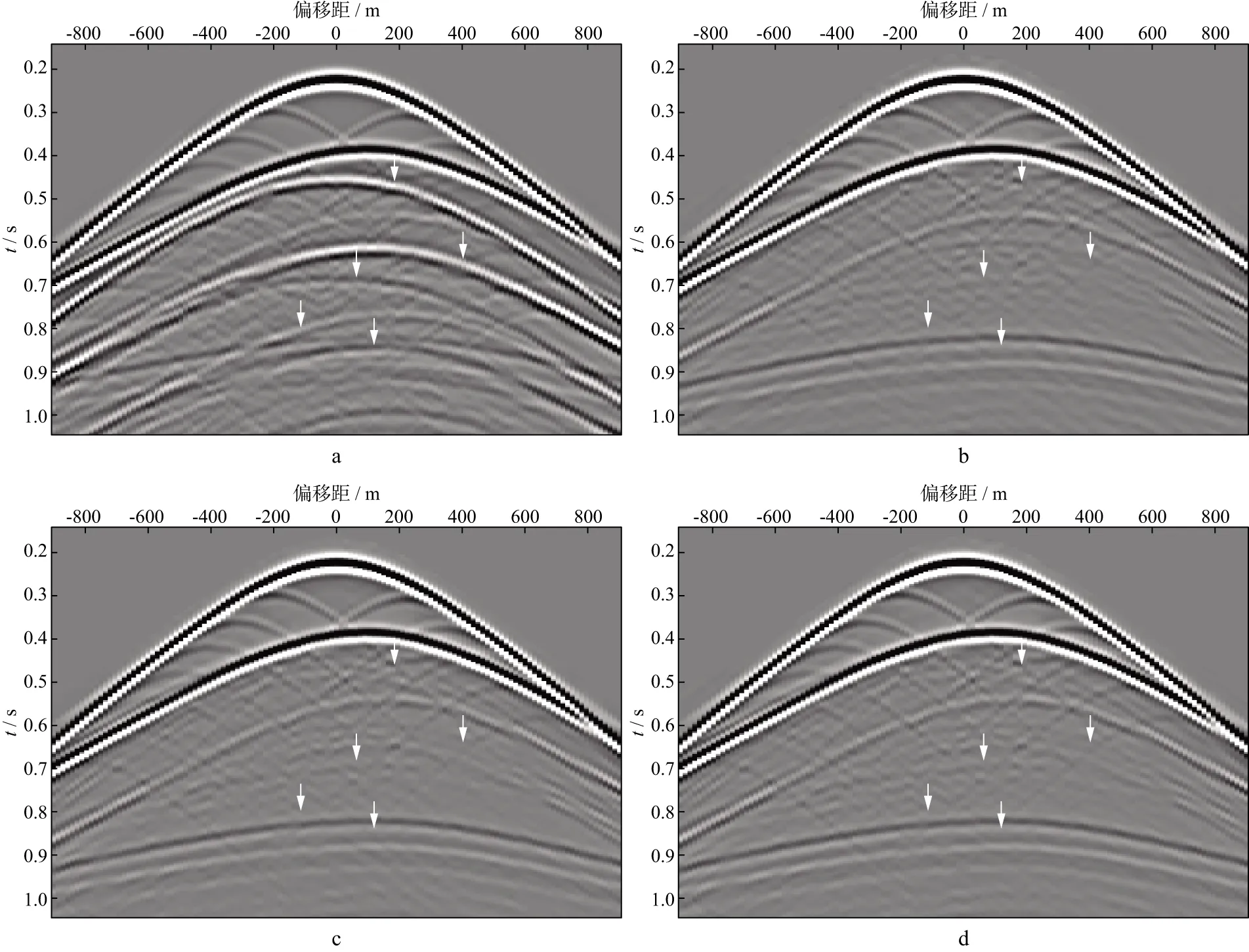
图5 输入不同相位子波的多次波压制结果a 原始数据; b 零相位子波; c 最小相位子波; d 混合相位子波

图6 不同相位子波输入时的子波迭代更新结果a 零相位子波; b 最小相位子波; c 混合相位子波

2.2 实际数据算例

实际地震数据来自苏伊士湾海上地区(Gulf of Suez region),浅海底产生了强烈的多次波,每炮178道,采样间隔为4ms,记录长度为4s。初始子波使用20Hz零相位Ricker子波。

图7a为包含多次波的原始单炮记录,整个数据体被强烈的多次波覆盖。图7b为采用本文方法进行多次波压制后的单炮记录,可以看出,不同阶次的多次波都得到很好的压制,一次波得到恢复。

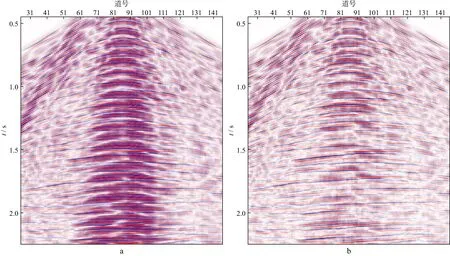
图7 采用本文方法进行多次波压制前(a)、后(b)的单炮记录

图8a为原始数据叠加剖面,多次波在剖面中普遍存在。图8b为采用本文方法进行多次波压制后的叠加剖面,可以看出,海洋表面相关各阶多次波得到很好的压制。

采用本文方法迭代求解时的子波变化情况如图9 所示。可以看出,初始子波(k=1)经过5次迭代,子波趋于稳定收敛,第4次迭代(k=4)和第5次迭代(k=5)的子波几乎重合。

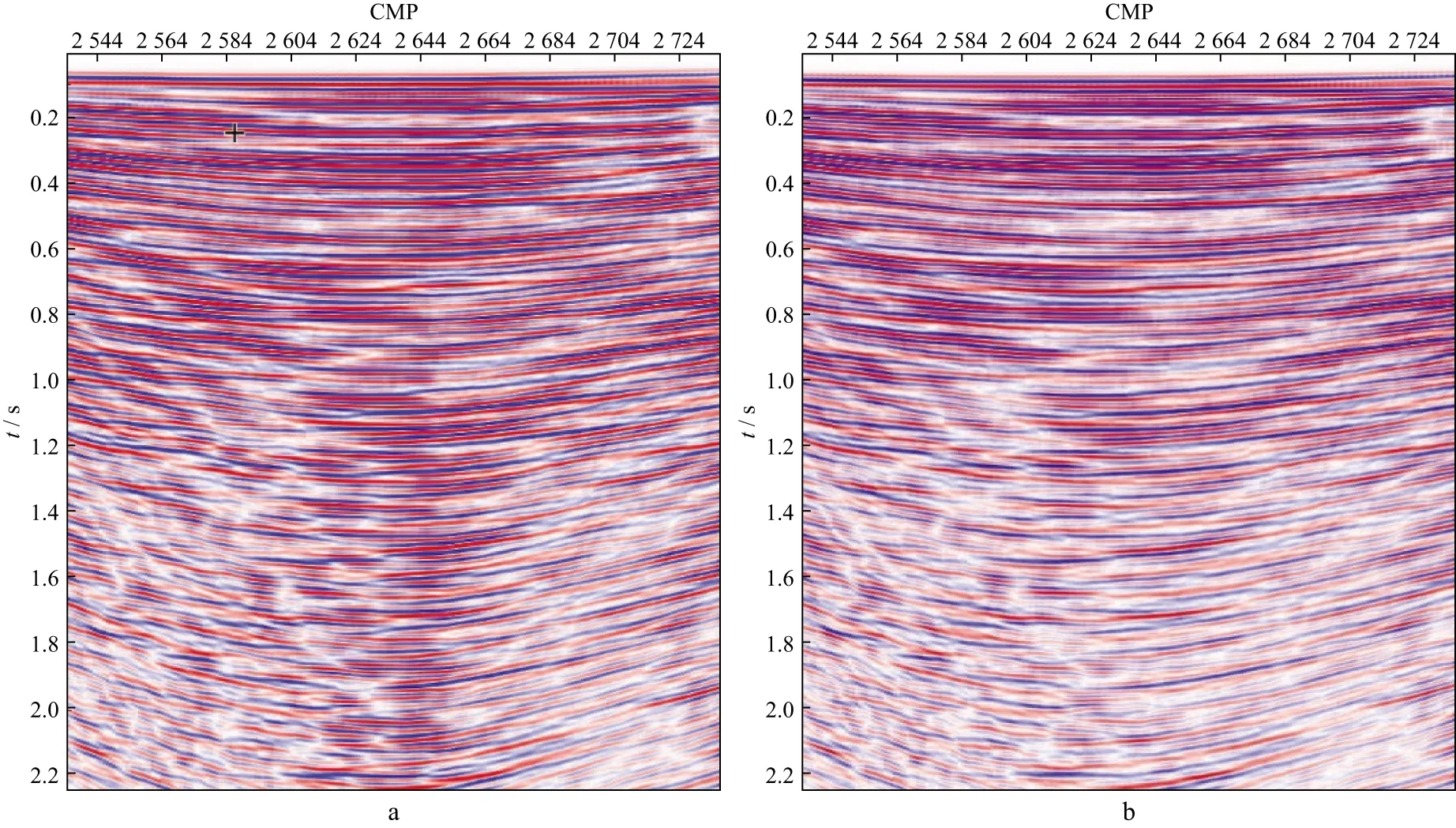
图8 采用本文方法进行多次波压制前(a)、后(b)的叠加剖面

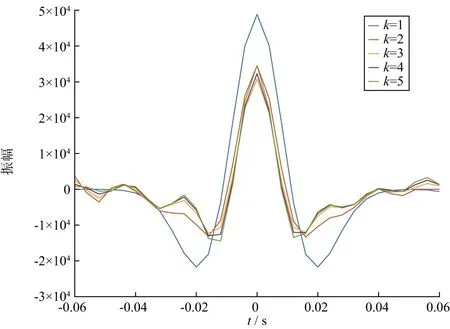
图9 采用本文方法迭代求解时子波变化情况

3 结论

本文以EPSI多次波压制方法频域理论公式为基础,将EPSI过程表示为双线性算子一次波脉冲响应和震源子波的约束优化问题,提出了一种自适应稀疏反演多次波压制方法(AEPSI),在迭代求解的过程中,震源子波的主频、振幅、相位等特性,自适应逐步逼近实际地震子波,避免了通过输入记录的多维互相关数据来估计初始震源子波的不确定性以及求取一次脉冲响应时的人工拾取和时窗设置。模型数据和实际资料处理结果表明,本文方法正确有效,稳定收敛,对子波误差具有较高的容忍度,整个处理过程完全由数据驱动,无需人工干预,具有较好的应用前景。