基于问题驱动,多维度落实解题教学
2021-05-14徐艳
徐艳
一、学情分析
本节课为习题课,在此之前学生已经学习并掌握了一次函数的概念、图像及性质,对一次函数与一元一次方程、一元一次不等式之间的关系有了一定的认识,能够初步解读一次函数的图像,并能运用读取的信息,数形结合地解决简单的实际问题。但学生对函数图像的解读大多停留在较为无序的感知阶段,对复杂情境中的函数图像,难以准确地读取信息,因而无法顺利地解决问题。
该从哪些角度层层解读,从而获取足够多的信息,再结合函数与方程、不等式等模型的关系来解决问题呢?本节课尝试以问题驱动探究,从不同维度逐层深入地解读一次函数图像,从而帮助学生顺利地解决函数类问题。
二、教学实录
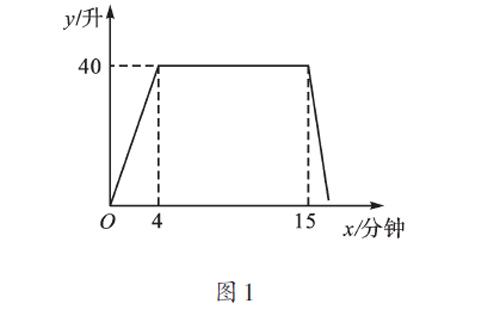
问题1 某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时,洗衣机中的水量y(升)与时间x(分钟)之间的关系如图1所示。根据图像解答下列问题:
(1)洗衣机的进水时间是多少分钟?清洗时洗衣机中的水量是多少升?
(2)已知洗衣机的排水速度为每分钟19升。
①求排水时水量y与x之间的表达式;
②如果排水时间为2分钟,求排水结束时,洗衣机中剩下的水量。
师:读图,首先请根据题意弄清x、y分别表示的量是什么。
生1:根据题意,x表示洗衣机工作的时间,y表示洗衣机中的水量,函数图像表示工作时洗衣机中的水量与工作时间之间的关系。
师:你能根据图像解读一下变化过程分为几段吗?水量随着时间的变化是怎样变化的呢?
生2:从变化过程来看,第一阶段,洗衣机中的水量随着时间的增加而增加,即进水阶段;接着一段时间内,水量保持不变,即清洗阶段;最后,水量随着时间的增加而减少,即排水阶段。
师:很好!下面我们从几个具体的维度来解读这个函数的图像。
维度1 图中有哪些点是已知的?它们对应的实际意义是什么?
生3:图中已知的点有(0,0)、(4,40)、(15,40)。其中(0,0)表示洗衣机没有开始工作时,水量为0;(4,40)表示洗衣机开始工作(进水)4分钟时,水量为40升;(15,40)表示洗衣机工作15分钟(并不是清洗15分钟)时,水量仍为40升。
维度2 图中有哪些线是可以直接用待定系数法求出表达式的?
生4:图中第一阶段的线段(0≤x≤4)上有两个已知点(0,0)、(4,40),因此,我们可以用待定系数法直接求得其对应的函数表达式为y=10x;第二阶段的线段(4
维度3 根据已知数据,你能得出每一阶段水量变化的速度,然后具体地描述这次洗衣服的过程中,洗衣机水量的变化情况吗?
生5:前4分钟,水量均匀增加,洗衣机处于进水状态,4分钟进水40升,因此,进水的速度为40÷4=10(升/分钟);4—15分钟这11分钟内,洗衣机处于清洗状态,水量保持40升不变;15分钟后,水量均匀减少,洗衣机处于排水状态,排水速度为每分钟19升(已知)。
师:水能完全排空吗?相应的图像有什么特征呢?
生6:水并不能完全排空,最后的水量要经过脱水才能为0,因此,图像到最后并没有与x轴相交。
维度4 根据维度3中描述的实际变化情况,你能设法求出洗衣机排水状态所对应的第三阶段线段的函数表达式吗?
生7:可以用待定系数法。但这里只有一个点,无法确定k、b啊,因此,我们还需要再知道一个点的坐标。
师:再找哪一点呢?读题,根据“排水速度为每分钟19升”,你可以得到什么启发呢?
生8:可以求得当x=16(即排水1分钟)时,水量为40-19×1=21(升),由此可得第二个点(16,21)。由点(16,21)、(15,40),可用待定系数法求得对应函数表达式为y=-19x+325。
生9:或者求出排水2分钟后的水量,同样可求得函数表达式,同时完成第(2)②问。
生10:也可以用虚线延长线段与x轴相交,求得交点横坐标为15+40÷19=17[219],从而确定交点坐标为(17[219],0),进而用待定系数法求得函数表达式。
师:大家根据题中“排水速度为每分钟19升”这一信息,找出了1分钟后、2分钟后、如果能排光等多个不同的点,这些点都可以用来求函数表达式,非常好!
生11:我觉得可以不用待定系数法,根据实际意义就可以直接列式。由题意,排水时的水量=排水前清洗时的水量-排出的水量,用式子表示即为y=40-19×(x-15),化简得y=-19x+325。
师:特别地,每一段水量变化的速度,与对应的函数关系式中的│k│完全一致。水量增加,k为正数;水量减少,k为负数。从第一阶段图像对应水量变化速度为每分钟10升,即可知道该段图像对应的函数表达式中的k=10;由排水阶段的水量减少速度为19,即可知道该段图像对应的函数表达式中的k=-19。反之,已知k,也就知道了变化速度。
用待定系数法求函数表达式是常规解法,而根据实际意义找到数量关系,再直接列式表示函数表达式显得更简便,在一次函数类问题中也非常实用。但这要求学生善于思考,能将函数问题回归实际数量关系。
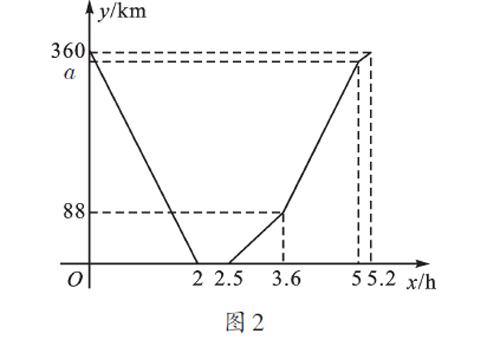
问题2 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶。图2中折线表示快、慢两车之间的距离y(km)与它们的行驶时间x(h)之间的函数关系。小欣同学结合图像得出如下结论:①快车途中停留了0.5h;②快车速度比慢车速度快20km/h;③图中a=340;④快车先到达目的地。其中正确的是( )。
师:读图,首先请根据题意弄清x、y分别表示的量是什么。
生12:根据题意可知x表示两车出发后行驶的时间,y表示两车之间的距离,函数图像表示两车之间的距离与行驶时间之间的关系。
师:你能根据图像解读一下变化过程分为几段吗?两车之间的距离随着时间的变化是怎样变化的呢?
生(思考、讨论、交流、陈述):从变化过程来看,第一阶段两车之間的距离随着时间的增加而减小,即相向而行直到相遇;接着的0.5h内距离一直为0,即两车相遇后停留休息;然后两车距离随着时间的增加而增大,但很显然,变化的速度比两车相向而行时慢得多,说明只有一辆车在行驶,另一辆车原地不动;接着两车之间的距离随着时间增加而增大,目测变化速度与相向而行时一致,可见两车均以原速背向行驶;最后一小段图像,两车之间的距离变化速度再次变小,表明有一辆车到了,仅另一辆车在行驶,最终到达各自终点。
师:大家描述的运动过程很清晰,下面从几个具体的维度来解读这个函数的图像。
维度1 图中有哪些点是已知的?它们对应的实际意义是什么?
生13:图中已知的点有(0,360)、(2,0)、(2.5,0)、(3.6,88)、(5.2,360)。其中(0,360)表示准备出发时两车相距360km,说明两地之间的距离为360km;(2,0)表示2h后两车相遇;(2.5,0)表示2.5h起,其中一辆车准备出发;(3.6,88)表示3.6h时,两车之间距离为88km,此时另一辆车准备出发;(5.2,360)表示5.2h时,两车各自均已到达终点。另外,(5,a)表示自出发行驶到5h时,两车相距akm,其中一辆车到达终点。
维度2 图中有哪些线是可以直接用待定系数法求出表达式的?
生14:根据维度1读出的已知点可知,0≤x≤2、2 维度3 根据已知数据,你能得出每一段路程变化对应的速度,然后具体地描述这段行程吗? 生15:两车开始相距360km,2h后相遇,由此可知两车速度之和为360÷2=180(km/h);2h—2.5h,两车相遇后距离一直为0,两车停住休息;2.5h—3.6h这1.1h,两车间距均匀增大为88km,因此变化速度为88÷1.1=80(km/h),显然是慢车的速度,由此可知快车的速度为180-80=100(km/h);3.6h—5h,两车间距变化的速度变大,变得和最初2h的速度相当,即为180km/h,故而求得a=88+180×(5-3.6)=340(km);5—5.2h,0.2h的间距变化为360-340=20(km),因此速度为20÷0.2=100(km/h),即只有快车在行驶,慢车已于5h时到达终点;5.2h时,快车也到达终点。 师:至此,本题所有答案都已解锁。 维度4 根据维度3中描述的实际变化情况,你能设法求出3.6 生16:由维度3可知,3.6h—5h,两车间距变化的速度为180km/h,因此本段函数式中的k=180,两车间距离=3.6h时的间距+增加的距离,即y=88+180×(x-3.6)。当x=5时,可得a=y=88+180×(5-3.6)=340。由待定系数法求得当5 三、教学反思 本节课,在探究两个问题的解题过程中,4个维度的问题设计分别为:维度1,引导学生探究关键点;维度2,探究关键线段;维度3,定量地探究实际变化过程;维度4,用数学模型解决实际问题。教师通过这4个维度引导学生逐层深入地读取图像中的有效信息:从整体看图像的变化趋势,定性地描述整个变化过程;从局部看关键点、线段的数量及实际意义,进而定量地描述变化过程,顺利解决问题。总之,我们要教会学生一些通法,即先通过图像获取信息,再从点、线、变化过程等多个维度去读图、识图、用图,充分挖掘有用信息,然后才能数形结合地破解一次函数应用问题,以此推广到以后学习的各类函数图像问题。 (作者单位:江苏省南京市竹山中学)
