黔西突出煤的微观孔隙分形特征及其对渗透率的影响

2021-05-14薛海腾李希建陈刘瑜

煤炭科学技术 2021年3期

薛海腾，李希建，陈刘瑜，刘钰

（1.贵州大学矿业学院，贵州贵阳 550025；2.复杂地质矿山开采安全技术工程中心，贵州贵阳 550025；3.贵州大学瓦斯灾害防治与煤层气开发研究所，贵州贵阳 550025；4.中国电建集团贵州电力设计研究院有限公司，贵州贵阳 550003）

0 引言

煤的渗透率是表征煤层气产量及瓦斯运移规律的重要指标，同时也是防治瓦斯灾害的重要参数［1-3］。研究［4］表明煤体的渗透特性具有分形特征，且煤的渗透率与其微观孔隙和裂隙分布有密切关系，因此，利用分形理论研究煤的微观孔隙结构特征对瓦斯吸附能力及瓦斯渗透性的影响具有重要的意义。近年来，诸多学者利用分形理论研究了煤的孔隙结构及其渗透特性。高为等［5］基于压汞试验，运用分形理论探讨了分形维数与煤储层孔渗性的关系。李子文等［6］将高压容量法与液氮吸附试验相结合，研究了不同压力阶段分形维数对瓦斯吸附的影响。郭德勇等［7］得出孔隙度与渗透率的关系，表明渗透率随孔隙度的变化呈幂函数增长。姜文等［8］运用分形理论研究了页岩的孔隙分形特征。宋晓夏等［9］分析了构造煤吸附孔分形维数与吸附能力的关系，指出分形维数越高，孔表面越粗糙，微孔含量越多，吸附能力越强。宋昱等［10］将压汞试验与液氮吸附试验相结合方法，分析了menger、热力学、sierrpinski 和FHH 分形模型对构造煤的适用性。降文萍等［11］分析了不同结构煤体的孔隙特征，说明了煤体破坏强度越大，比表面积和孔体积的分形维数越高，越容易发生煤与瓦斯突出。胡耀清等［12］揭示了裂隙发育与分形维数的关系，得出煤体的渗透率与分形维数呈正指数函数关系。

综上所述，应用分形理论描述煤的孔隙结构，及其对吸附性能和渗透能力的影响研究取得了一定的进展，但都未考虑煤孔隙迂曲度及毛细管对其吸附性能及渗透性的影响。因此，笔者以青龙煤矿和兴隆煤矿的构造煤和原生煤为研究对象，通过计算不同煤样毛细管平均迂曲度分形维数DT，分析了DT对瓦斯吸附及其渗透率的影响，为进一步开发该地区煤层气及瓦斯灾害防治提供重要参考。

1 试验

试验样品分别取自青龙煤矿16 煤遇断层处构造煤和原生结构煤，兴隆煤矿1802 运输巷约258 m处原生煤和1802 回风巷约149 m 断层带处构造煤。利用全自动工业分析仪对煤样进行工业分析，通过美迪全自动密度仪进行煤样表观／骨架密度测定，测得的结果见表1。

液氮吸附孔径测定采用贝士德3H-2000PS1／2型静态容量法比表面及孔径分析仪对4 种煤样进行孔径分析，孔径测试范围为0.35 ～400.00 nm，试验所测煤样孔隙参数见表2。在恒温下，对应一定的吸附质压力，在固体的表面上存在一定量的气体吸附，通过测定一定压力下的吸附量，可以得到吸附等温线。试验所测4 种煤样的液氮吸附曲线如图1 所示。图1 中，p0为气体吸附达到饱和蒸气压；p 为平衡压力；p／p0为相对压力。

表1 煤样参数Table 1 Coal sample parameters

表2 孔隙参数Table 2 Pore parameters

由图1 可知，除青龙煤矿原生煤煤样，其余煤样在相对压力较小（p／p0＜0.3）时，均出现明显的滞后现象，而青龙煤矿原生煤煤样吸附解吸等温曲线重合，究其原因在低压阶段青龙煤矿原生煤煤样微孔尤其发育，难以发生毛细管凝聚现象，滞后现象消失，在此阶段气体分子和煤体之间的作用力主要是范德华力；随着相对压力升高且逐渐趋向于1 时，4种煤样吸附等温曲线和解吸等温曲线先升高后逐渐趋于重合，此时气体分子和煤体之间的作用力主要是毛细管凝聚力。由此说明在不同的压力阶段煤体吸附甲烷的机制有很大的差异。同时由图1 可知，在相对压力约为0.5 时，构造煤和原生煤解吸等温曲线均出现“拐点”，也表明不同压力段煤对气体的吸附具有差异。不同压力阶段煤对气体吸附性差异主要受到煤体微观孔隙结构的控制，而分形维数可以更好地表征煤的微观孔隙结构特征，因此，分析煤体的微观孔隙分形特征，可以更好地深入分析其对煤的渗透率的影响。

图1 液氮吸附／解吸等温曲线Fig.1 Adsorption／desorption isotherm curves of liquid nitrogen

2 煤的孔隙分形特征与渗透率的关系

2.1 分形维数计算

利用液氮吸附试验计算分形维数的方法有BET（Brunauer-Emmett-Teller）模型、FHH（Frenkel-Halsey-Hill）模型、热力学模型等，其中FHH 模型应用最为广泛，计算方法为［13］

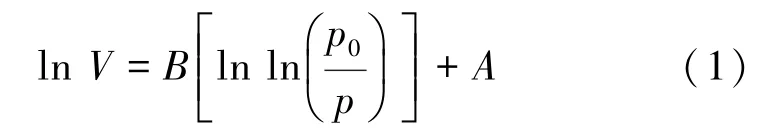
式中：V 为平衡压力p 下的气体吸附量，cm3／g；B 为拟合直线斜率；A 为常数。

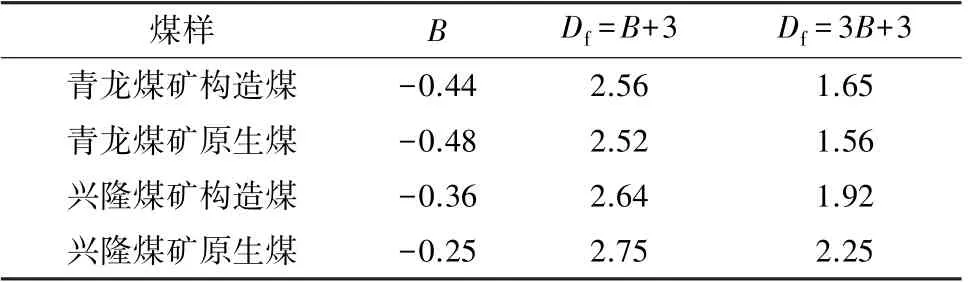
表3 分形维数计算结果Table 3 Calculation results of fractal dimension

依据前人研究成果［4，8］，B 与分形维数Df成线性关系，通常有2 种计算式：Df＝B＋3 和Df＝3B＋3。采用2 种方法计算的分形维数结果见表3，根据分形维数的数值范围（2＜Df＜3）可知：用公式Df＝K＋3计算结果与实际更符合。因此，笔者计算分形维数的公式为

2.2 毛细管平均迂曲度分形维数

煤岩是典型的多孔介质，其内部大量孔隙形成了非常复杂的流体运移通道，瓦斯在通道内流动的迂回程度可由迂曲度τ 表示，表达式［14］为

式中，φ 为孔隙度。

二维空间毛细管的特征长度Lm可表示为［15］

式中：Df为分形维数，二维空间内，1＜Df＜2，三维空间内，2＜Df＜3。

COSTA［16］认为三维空间和二维空间孔隙分形维数的数值差为1，因此可以用二维空间孔隙分形维数求得三维空间孔隙分形维数； rmax为最大孔隙半径，μm。

毛细管平均迂曲度分形维数DT和迂曲度τ、平均毛细管半径rav的函数关系为

式中：rav为平均毛细管半径，rav＝Dfrmin／（Df-1）；rmin为最小孔隙半径，μm。

将孔隙度代入式（3）可求得煤体孔隙迂曲度，由式（4）可得煤岩毛细管特征长度，将式（3）、式（4）所得结果代入式（5）可得煤岩毛细管平均迂曲度分形维数DT，计算结果见表4。

2.3 DT、τ 对瓦斯吸附的影响

煤的吸附能力与其物理性质有着极其重要的关系。在Langmuir 方程中VL代表最大单分子层的吸附能力；PL代表吸附量达到VL一半时的压力，因此DT、τ 与VL、PL有着密切的联系，如图2 所示。

表4 毛细管平均迂曲度分形维数计算结果Table 4 Calculation result of capillary mean tortuosity fractal dimension

图2 DT、τ 对瓦斯吸附的影响Fig.2 Effect of DT and τ on gas adsorption

随着DT、τ 的增大，VL逐渐增大，PL逐渐减小。主要是因为随着DT的增大，煤孔隙表面越粗糙，比表面积越多，可供瓦斯吸附的点位增多，而随着τ 的增大，瓦斯运移所经过路径复杂，瓦斯难以从煤层中释放出来，故瓦斯的吸附能力增强。而PL逐渐减小，说明瓦斯吸附时所需的能量减少，瓦斯吸附速度加快，反之说明，VL增大，PL减小，更有利于瓦斯解吸。

2.4 DT对渗透率的影响

煤岩渗透率与其孔隙度和微观孔隙结构有密切关系，通过分形维数、孔隙度及迂曲度与渗透率的关系可估算出其理论值，其表达式为［17］

式中：K 为渗透率，10-3μm2；β 为常数，β ＝4π／3。

将上述所得参数代入式（6）可得构造煤和原生煤的理论渗透率K。

渗透率是反映煤岩储层渗透特性的重要参数，其大小与煤岩表面粗糙程度以及孔隙结构的复杂程度有一定的相关性。由图3 可知，无论是构造煤还是原生结构煤，渗透率K 随DT的增大而减小，两者具有较好的负相关性（图3）。

对同一研究区煤样，青龙煤矿构造煤的渗透率K均小于原生煤，但随着DT的增加，兴隆煤矿构造煤的渗透率逐渐大于原生煤，究其原因贵州省区域煤层都较为复杂，无论是原生煤还是构造煤，其原生孔隙结构受破坏程度较大，孔隙结构都较为复杂，渗透性较差，与其他区域内的煤有较大区别，这也是贵州省矿区频发煤与瓦斯突出的重要原因。