深刻认识“在误差允许范围内”——以电火花打点计时器测速度为例

戴耀东

(海门市证大中学，南通 海门 226100)

我们经常说“在误差允许范围内……”,误差允许的范围究竟是多大?我们的实验结果真的在误差允许的范围内吗?笔者将利用误差分析理论,定量计算误差允许范围,为我们评估实验数据分析提供参考．

1 误差传递理论介绍[1-2]

假设直接测量数据为x,y,z……,其对应误差为Δx,Δy,Δz……,间接测量数据为q,其对应误差为Δq.

若间接测量数据与直接测量数据的关系为q=x+y-z……,则误差为

Δq=Δx+Δy+Δz…….

电火花打点计时器测速度的实验中,时间与长度为直接测量数据,速度为间接测量数据．

2 直接测量数据的误差估计

电火花打点计时器测速度过程中,主要的误差来源有电源频率浮动带来的时间误差,刻度尺测量误差与点迹直径大小造成的长度误差．

2.1 时间误差

笔者从国家电网官网查得,民用电正常运行电源频率为50.0 Hz,误差不超过±0.2 Hz.记为Δf=±0.2 Hz.

2.2 长度误差

常用的毫米刻度尺在进行测量时,读数不可避免会产生误差．

如图1,我们可以合理确定所示长度肯定更接近36 mm,由于刻度尺最小分度为1 mm,估读误差取一个分格的一半,即0.5 mm,因此这里的长度为36 mm,误差为±0.5 mm.记为Δx1=±0.5 mm.

图1

同时,查询说明书可知,电火花打点计时器(以LJ-DJ-F-20(J0207)为例)打下的点迹是有大小的,直径≤0.8 mm,测量点迹位置时会以中心为参考点,因此点迹位置读数的最大误差为±0.4 mm.记为Δx1=±0.4 mm.

于是,在用毫米刻度尺测量纸带上点迹之间的长度时,误差包含了点迹中心的读数误差、刻度尺估读误差,此两项误差不独立,即点迹中心误差的读数误差上叠加了刻度尺估读误差,因此,此实验的长度误差Δx=Δx1+Δx2.记为

Δx=Δx1+Δx2=±0.9 mm.

3 间接测量数据的误差估计

本文用到笔者发表在2013年12期《物理教师》上的《探究逐差法处理纸带时奇数段位移该如何取舍》中的第9组数据,以此为例具体计算相关物理量．

3.1 原始实验数据[3]

表1

3.2 速度及对应误差

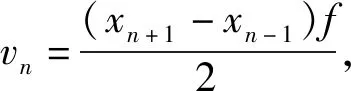
图2

代入数据,在Excel中编辑公式可求各点速度及对应误差,如表2.

表2

在Excel中画带误差条的v-t图像,可得

3.3 结果分析

如图3,拟合的直线虽然没有经过所有点,但经过1、2、3、5、7、8点的误差条,可知: ① 第4、6两点需舍弃; ② 其他点满足线性关系v=9.40t+0.90.

图3 v-t图

因此我们可得出结论:“在误差允许范围内”物体在做匀加速直线运动．

4 小结

本文利用误差分析理论定量计算了打点计时器测物体速度时误差,把高中常用的“在误差允许范围内”这句术语进行了深刻剖析,旨在表明,只有在合理的科学的误差估计的前提下,我们才能有理有据地说出“在误差允许范围内”．