基于前馈神经网络的等离子体光谱诊断方法*
2021-05-14王彦飞朱悉铭2张明志孟圣峰贾军伟柴昊王旸宁中喜2
王彦飞 朱悉铭2)† 张明志 孟圣峰 贾军伟柴昊 王旸 宁中喜2)‡
1) (哈尔滨工业大学, 哈尔滨 150001)
2) (工信部“航天等离子体推进”重点实验室, 哈尔滨 150001)
3) (北京东方计量测试研究所, 北京 100086)
光谱诊断在等离子体刻蚀、材料处理、等离子体设备和工艺开发, 以及航天等离子体推进等领域得到了广泛的应用.光谱诊断依赖的碰撞辐射模型会受到碰撞截面等基础物理数据所含偏差的影响, 导致诊断结果出现误差.针对这一问题, 本文开发了一种基于前馈神经网络的等离子体光谱解算方法.通过对比新方法与以往常用的最小二乘诊断方法的误差特性, 发现神经网络诊断方法能够通过辨识光谱向量的主要特征, 减小基础数据偏差向诊断结果的传递.对实验光谱数据的分析进一步印证了这一点.本文还对神经网络算法对抗基础数据偏差的机理进行了分析.这种方法在等离子体参数在线监测、成像监测海量数据处理等领域具有良好的应用前景.
1 引 言
随着集成电路中半导体器件集成密度和复杂度的不断提高, 半导体器件的尺寸不断缩小, 对刻蚀、材料处理等工艺流程的加工精度提出了日益严苛的要求.在上述工艺中, 实时监测刻蚀速率、掌握加工进程, 对于保证加工精度、提高产品良率、控制加工成本有重要的意义, 是更高水平的新制程工艺开发中不可或缺的手段[1−3].等离子体发射光谱诊断是一种非浸入式的监测方法, 能够在不干扰等离子体的前提下实时原位地监测等离子体特征参数, 被广泛地应用于等离子体设备开发、运行状态监测和等离子体加工工艺流程开发中[4−8]; 凭借不易受高能离子束流轰击和复杂电磁场干扰的优点, 等离子体发射光谱诊断在航天等离子体推进领域也得到了广泛应用[9,10].
对等离子体发射光谱进行量化分析的基础是碰撞辐射模型.该模型通过求解等离子体中激发态粒子的速率平衡方程, 将发射光谱特性与等离子体密度、电子温度等特征参数建立联系.光谱诊断就是找寻模型预测结果与待测等离子体发射光谱的最佳逼近, 获取待测等离子体特征参数的过程.研究人员在这一领域开展了大量的研究工作.有研究者在氯、氧等离子体中混入氖、氩、氪、氙等示踪气体, 通过监测这些稀有气体的发射光谱, 实现对氯、氧等离子体中电子能量分布函数和电子温度的监测[11−13].发射光谱方法在材料表面处理等离子体设备中的等离子体动力学过程研究中的应用也得到了发展[14−16].研究人员面向使用氩、氮、氙、氪等工质的感性、容性耦合射频等离子体, 介质阻挡放电以及霍尔推力器等多种放电形式等离子体中电子温度、等离子体密度、气体温度等特征参数监测需求, 开展了一系列研究[17−19].
碰撞辐射模型对等离子体中激发、电离等物理过程速率的描述依赖于碰撞截面等基础物理数据.碰撞截面的主要来源有两个: 一是通过实验方法测量; 二是从第一性原理出发, 基于量子力学和原子物理学相关理论计算得到.在当前技术条件下, 通过实验测量所能获得的数据较为有限[20−23].由于信噪比、测量系统标定等方面的问题, 上述测量工作中普遍存在一定的测量误差.理论计算方面, 由于求解过程中涉及到碰撞体系中任意两电子坐标的相互纠缠, 求解过程需要使用多级展开的方法对体系进行描述, 并进行适当的截断处理, 这对截面计算结果的准确性产生了一定的限制[24−26].在这一背景下, 有部分研究人员通过向模型中引入调整因子对碰撞辐射模型使用的速率系数进行修正[11,27,28].然而, 由于等离子体中各种物理反应过程众多, 且相互耦合, 难以通过有限的实验对描述这些反应过程的截面数据进行恰当的修正, 导致截面数据所含偏差通过碰撞辐射模型向诊断结果传递, 给等离子体光谱诊断工作带来了困难.
近年来, 机器学习方法在物理领域得到了广泛的应用.经过训练的神经网络, 可构建起不同物理量间的映射关系.凭借在特征辨识方面具有的优势, 这一方法在诊断监测[29,30]、天体活动研究[31,32]、地球物理科学[33,34]、理论计算[35]等方面的应用得到了发展.常用的机器学习方法包括前馈神经网络、循环神经网络、残差神经网络等[35,36].前馈神经网络是一种神经元分层排列、各层神经元只与前一层中的神经元连接、层间不存在反馈的神经网络, 具有较强的多维映射能力[35], 适合解决光谱诊断这类问题.
本文以稀有气体放电为例, 基于前馈神经网络开发了一种能够辨识等离子体光谱特征, 减小截面数据偏差向诊断结果传递的光谱诊断方法.分析了以往常用的最小二乘拟合诊断方法与新方法的误差特性.并通过解算实验光谱数据, 进一步验证了基于神经网络的诊断方法对抗基础数据偏差的能力.
本文的章节安排为: 第2 节介绍文中使用的碰撞辐射模型, 第3 节介绍实验设置, 第4 节阐述使用的光谱解算方法和误差分析方法, 第5 节介绍神经网络的训练过程和验证结果, 对比最小二乘和神经网络两种诊断方法的误差特性, 并比较两种方法解算实验光谱数据的性能, 第6 节对全文进行总结.
2 碰撞辐射模型
本文的研究工作以一个稀有气体(氩、氪、氙)碰撞辐射模型为基础开展[10,18,19].碰撞辐射模型是描述等离子体中激发态粒子数密度分布的动力学模型.模型利用碰撞截面、速率系数等信息描述激发、电离、辐射等物理过程的速率, 通过构建和求解激发态粒子产生-损失速率平衡方程, 获得激发态粒子的密度分布和谱线强弱信息.
本文使用的碰撞辐射模型中考虑了以下动力学过程.
1)电子碰撞激发过程:
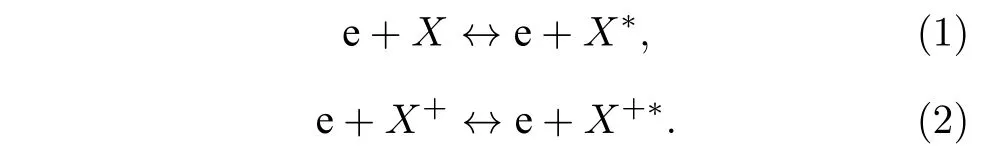
2)电子碰撞电离过程:
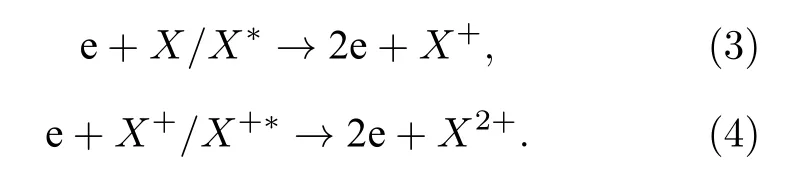
3)电子碰撞电离激发过程:
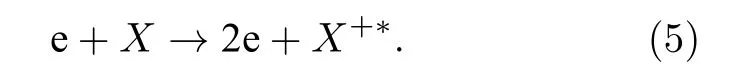
4)离子轰击激发和电离激发过程:
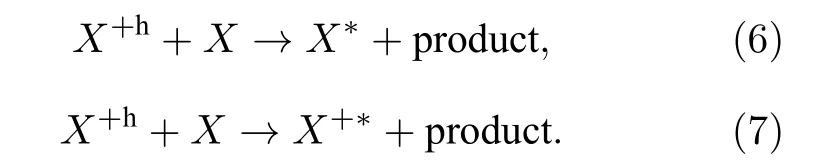
在(1)—(7)式中, e 代表电子,X代表稀有气体原子,X+代表稀有气体离子,X+h表示高能稀有气体离子, 上角标“ * ”表示该粒子处于激发态,product 表示反应的其他产物.除这些过程外, 模型中还考虑了激发态的自发辐射跃迁、亚稳态自吸收过程、电荷交换过程和粒子的迁移和扩散过程导致的壁面淬熄.
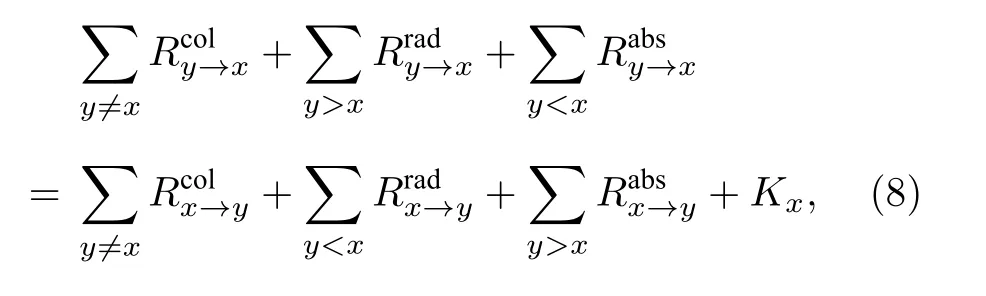
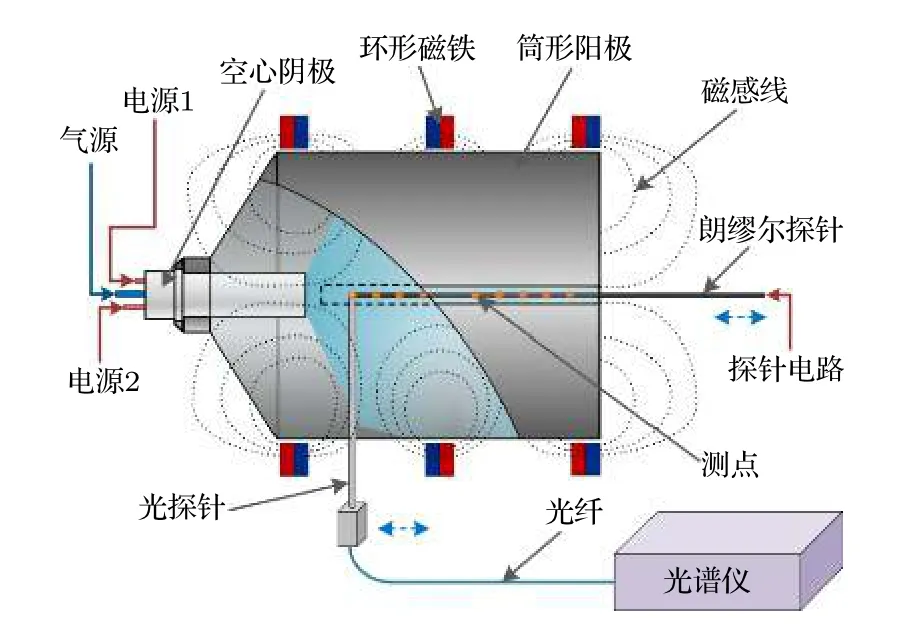
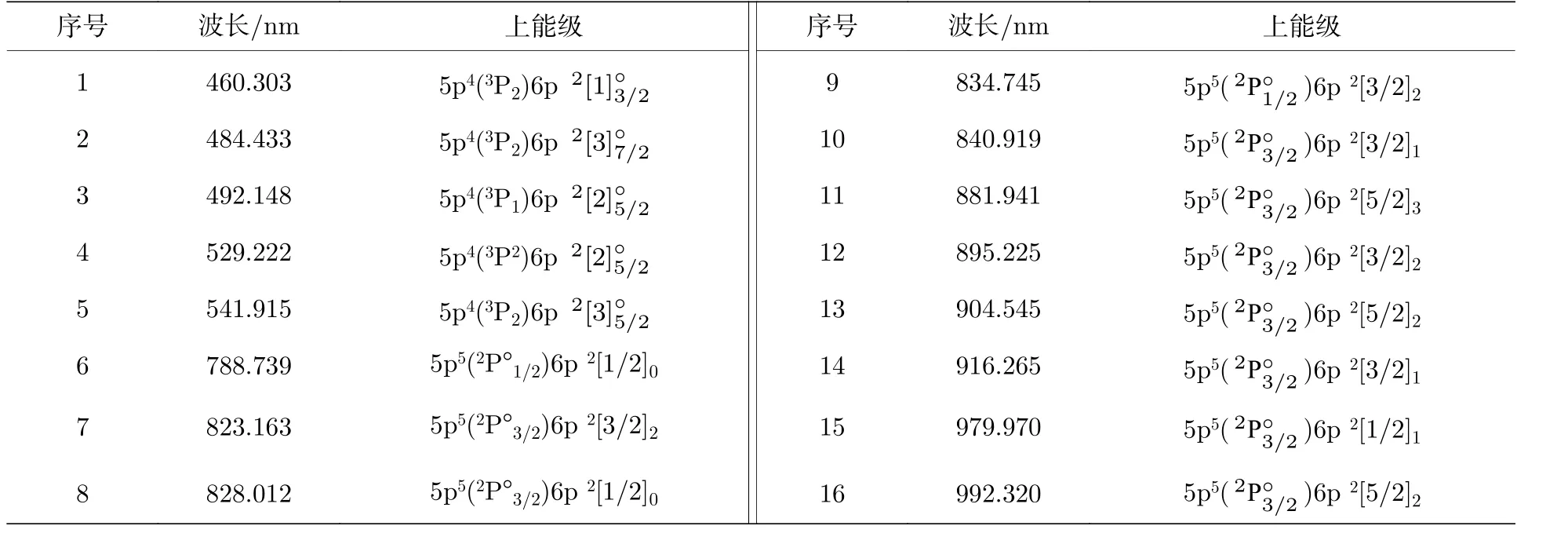
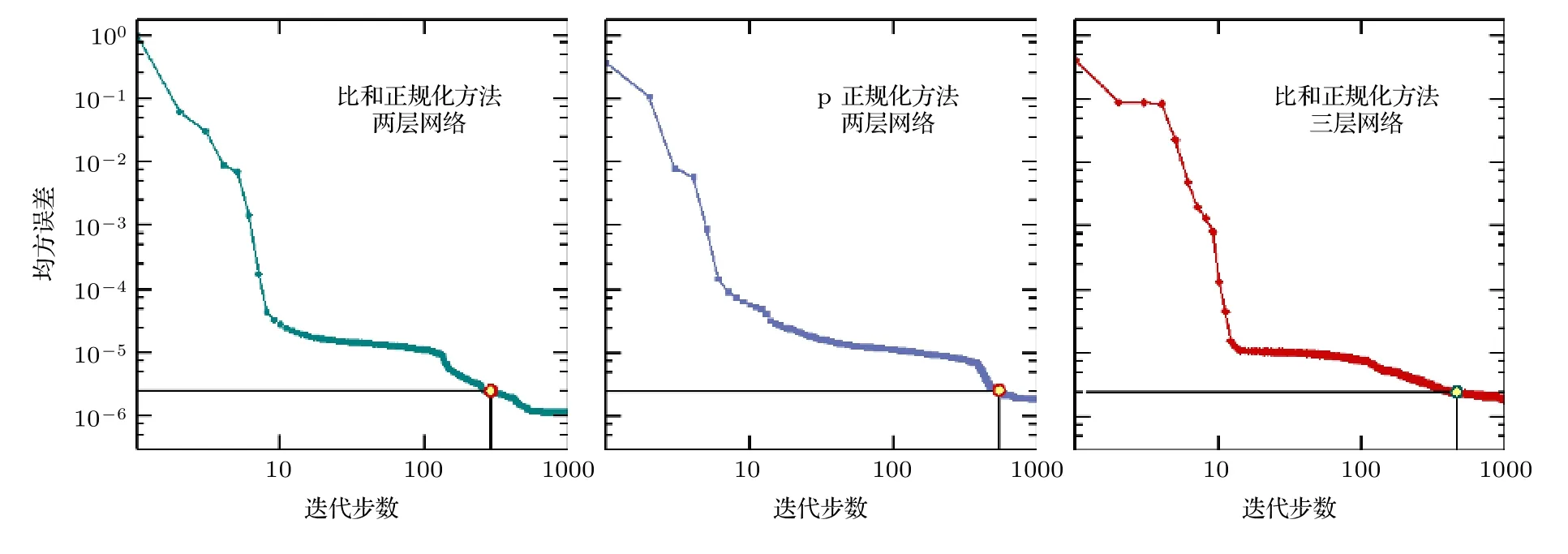
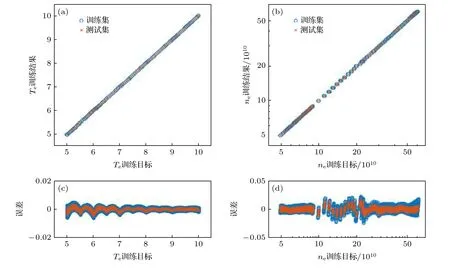
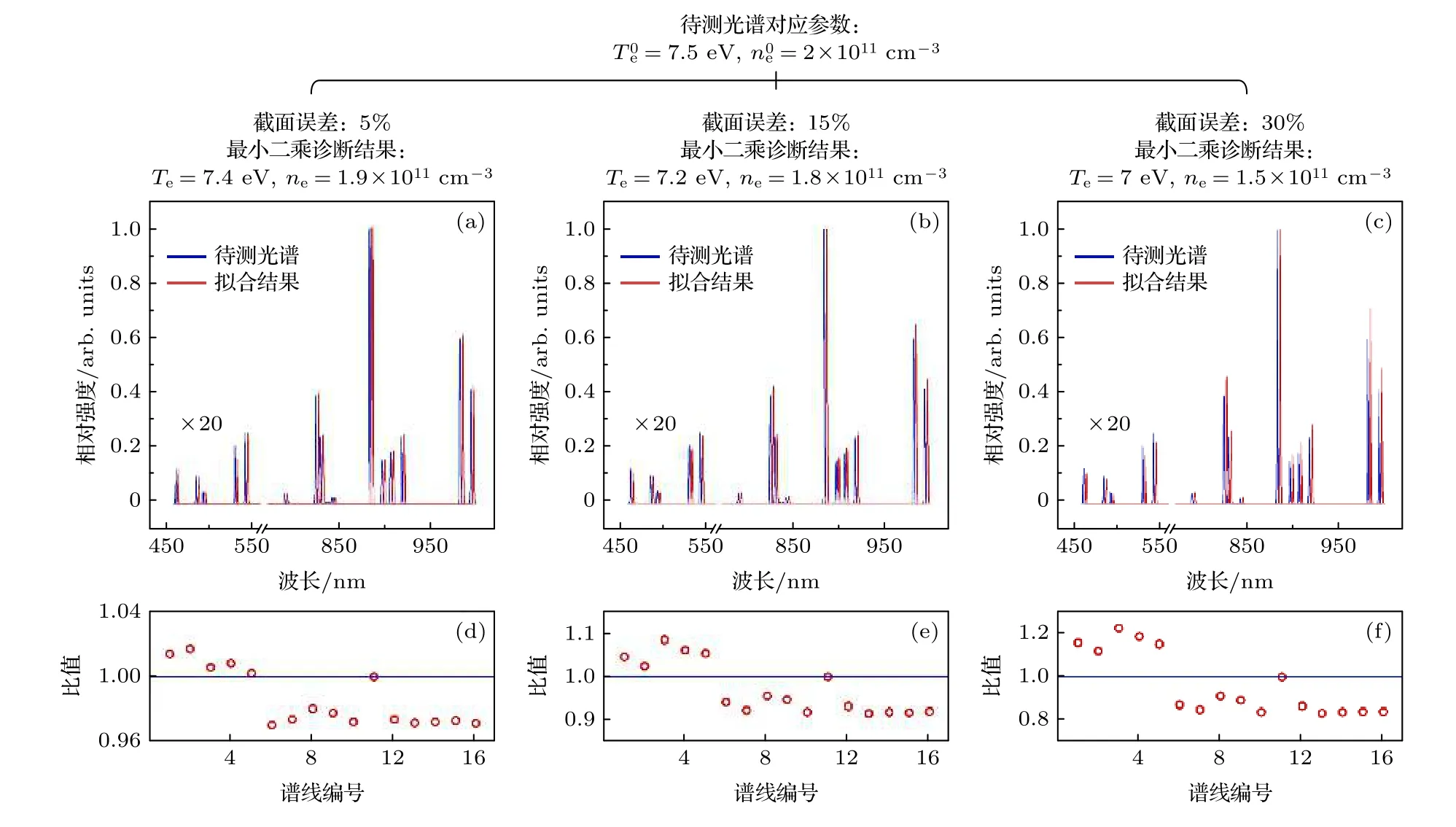
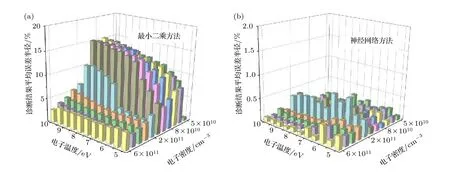
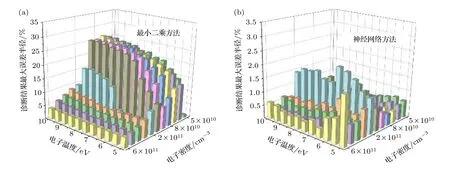
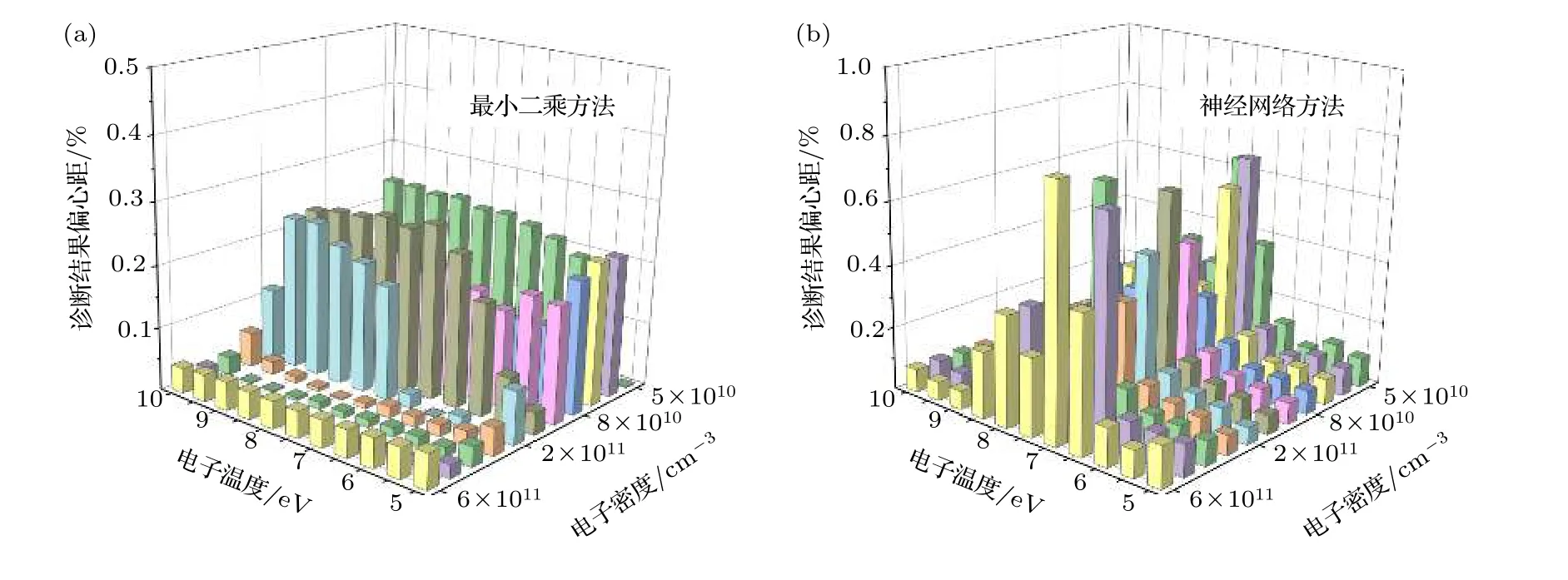
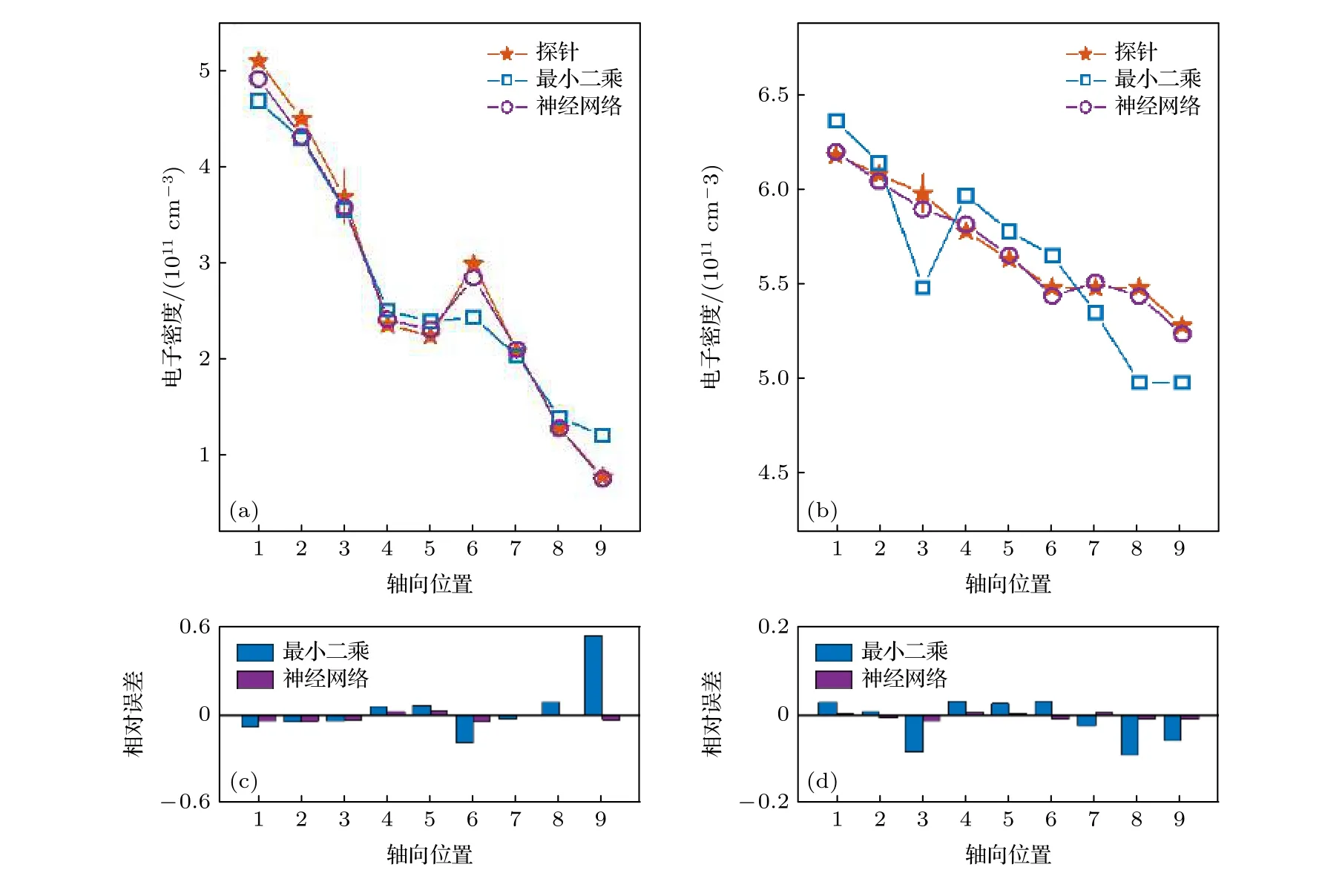
考虑这些过程, 激发态x的速率平衡方程写为这里R表示反应速率; “col”, “rad”和“abs”分别指碰撞、辐射和自吸收过程.K是由于壁面淬熄导致的损失率; 下标y指的是x之外的能级, 其中包括原子和离子基态能级(y 碰撞过程反应速率Rcol的计算需要使用速率系数Q, 计算公式为 这里σ表示碰撞过程的截面;E和m是电子能量和质量;E0是反应的阈值能量;g(E)是能量分布函数. 辐射和自吸收项则由下式给出: 式中,A是自发辐射的爱因斯坦系数,Γ是逃跑因子. 最后, 稀有气体原子由扩散导致的壁面淬熄频率由下式给出: 式中,D代表扩散系数,R代表等离子体尺度,v0为平均速度,χ01= 2.405. 将电子温度、电子密度等参数连同截面等基础数据代入, 联立求解方程(8)—(11), 可以得到激发态密度和等离子体发射光谱.本文以氙等离子体为例开展研究, 碰撞辐射模型求解所使用截面数据的详细描述和模型的实验验证见文献[10]. 本节对诊断实验使用的装置和测量方案进行介绍.实验中使用的装置如图1 所示.放电装置为一个考夫曼型等离子体源, 由空心阴极、环形钐钴磁铁、筒形阳极和石英筒组成.环形磁铁按同性磁极相对的方式排布, 在等离子体源内形成会切磁场位形.筒形阳极直径90 mm, 长86 mm, 侧面开有一8 mm 宽的窗口, 用于光谱采集.筒形阳极外安装一个石英玻璃筒, 避免电离室内气体从窗口泄漏. 实验中使用的朗缪尔探针为直径0.3 mm 的钨丝和陶瓷管制成的端面探针.光谱采集系统由Horiba FHR-1000 型光谱仪和Synapse CCD 探测器组成, 在400—1000 nm 波段的光谱分辨率优于0.05 nm.实验前使用卤钨灯校准光谱采集系统的光谱响应.采集光谱时, 光谱仪狭缝设置为20 µm,光探针垂直于等离子体源轴线布置.实验中, 使用步进电机驱动朗缪尔探针和光探针沿等离子体源轴向运动, 实现对等离子体源轴线上9 个不同测点处光谱和探针伏安特性的采集.实验时阴极供气流量为5 sccm (1 sccm = 1 mL/min), 电流为7 A.本文使用的实验装置与文献[37]使用的装置相同. 图1 考夫曼电离室结构及测量实验方案Fig.1.Structure of the Kaufmann discharge chamber and the scheme of measurement. 本节介绍数据分析方法.首先介绍基于最小二乘拟合的光谱诊断方法, 之后介绍基于前馈神经网络的光谱诊断方法, 最后对两种光谱诊断方法进行了比较. 首先对基于最小二乘拟合的光谱诊断方法进行介绍.碰撞辐射模型可看作如(12)式所示的, 以等离子体参数向量P为自变量, 以发射光谱向量I为因变量的函数, 而光谱诊断则可视为已知发射光谱向量I, 利用碰撞辐射模型F求参数向量P的过程.由于碰撞辐射模型较为复杂, 涉及到多种非线性过程, 方程(12)无法直接求解.研究人员常使用最小二乘拟合方法, 由待测光谱I*与模型预测光谱I构建误差函数, 迭代找寻待测光谱的最佳逼近, 来获得待测光谱对应的等离子体参数.图2 给出了这一方法的流程. 图2 基于最小二乘的光谱诊断方法流程Fig.2.Diagram of optical emission spectroscopy based on least square method. 表1 本文研究中选用的氙谱线表Table 1.Xenon spectral lines used in this work. 使用光谱中各谱线相对强度诊断等离子体参数的方法因为不需要对测量系统进行绝对标定, 在实践中得到了普遍应用[38−40].不失一般性, 本文使用如(13)式所示的, 利用所选谱线组中所有谱线对该组谱线强度总和作归一化的正规化方法(比和法), 获得表征谱线相对强弱关系的向量R: 本文以电子温度和电子密度为待诊断参数, 以刻蚀和材料处理中涉及的典型非平衡等离子体参数范围为例进行研究(电子温度5—10 eV, 电子密度5 × 1010—6 × 1011cm–3).在发射光谱方法常用的波长范围内, 选择了光谱诊断中常用的, 相对较强的16 条氙原子和氙离子谱线进行研究, 所选谱线见表1. 所选谱线构成的光谱向量I= [I1,I2, ···,I16]经比和法正规化后得到比和向量R= [R1,R2, ···,R16].由比和向量构建的误差函数为 使用莱文伯格·马夸特(Levenberg-Marquardt)方法寻找目标Te-ne范围中误差函数E的最小值.该值所对应的等离子体参数即为最小二乘方法的诊断结果. 基于前馈神经网络建立的光谱诊断方法流程和使用的神经网络结构如图3 所示.输入层由16 个神经元组成, 对应本文所选的16 条谱线; 输出层由两个神经元组成, 对应电子温度和电子密度2 个待测等离子体参数.本文选用一种双隐层结构(两个隐藏层分别含有10 个和5 个神经元)和一种三隐层结构(三个隐藏层分别含有12 个、8 个和4 个神经元)的网络结构进行训练.隐藏层使用S函数(Sigmoid)进行激活, 其表达式为 图3 基于前馈神经网络的光谱诊断方法流程Fig.3.Diagram of optical emission spectroscopy based on feedforward neural network. 训练神经网络所使用的数据集由碰撞辐射模型生成.考虑到本文使用的碰撞辐射模型在实验验证中存在10%—15%的偏差[10], 这里通过向模型所使用的截面数据上引入–30%—30%的均匀分布随机偏差, 模拟模型基础数据上可能存在的偏差,生成含有偏差的光谱构成训练集.参考其他使用神经网络开展的研究工作常用的方案, 对于两种网络结构, 使用模型生成数据集中80%的数据作为训练集, 并使用误差反向传播方法进行1000 次迭代;使用20%的数据作为测试集, 对训练结果进行评估.我们希望通过使用这种带有偏差的光谱数据对神经网络进行训练, 使网络能够对等离子体发射光谱的特征进行辨识, 降低基础数据偏差对诊断结果的影响. 分别利用由碰撞辐射模型和光谱测量实验获得的数据, 对前文介绍的最小二乘和神经网络两种光谱诊断方法进行比较和误差特性分析.一方面,使用碰撞辐射模型, 设定电子温度和电子密度并输入碰撞辐射模型生成光谱数据向量I0.分别使用最小二乘诊断方法和神经网络诊断方法对得到的光谱I0进行诊断得到诊断结果.并使用误差半径和偏心距, 通过分析两种诊断方法获得结果的误差特性对诊断方法进行比较.另一方面, 通过第3 节介绍的实验, 可获得考夫曼等离子体源电离室内的光谱数据向量IExp以及对应位置处朗缪尔探针测量的电子温度和电子密度分别使用最小二乘诊断方法和神经网络诊断方法对得到的光谱IExp进行解算, 并将两种方法获得的诊断结果与探针测得的进行比较, 进而对两种诊断方法进行比较.误差半径和偏心距的定义如图3 所示. 这里定义由第i条光谱获得的诊断结果对应的点与真实值对应的点间的距离为该点对应的误差半径ri, 距离真实值最远点的误差半径为最大误差半径rmax, 所有诊断结果对应的误差半径的平均值为平均误差半径rmean; 所有测量结果平均值与真实值对应的点间的距离定义为偏心距l.诊断方法获得的诊断结果的误差半径r和偏心距l越小, 诊断结果越接近设定值. 图4 误差半径及偏心距定义(真实值)Fig.4.Definition of error radius and eccentricity. 本节分为3 个部分.首先介绍本文开发的光谱诊断神经网络的训练和验证结果; 之后分析和讨论最小二乘和神经网络光谱诊断方法的误差特性, 并使用4.3 节中定义的误差半径和偏心距对两种方法进行比较; 最后, 对比两种诊断方法解算实验数据的表现. 本文训练神经网络所使用的数据由碰撞辐射模型生成.生成训练集使用的Te-ne组合由51 个Te和47 个ne值两两组合而成, 共计2397 种.所涵盖的参数范围为Te= 5—10 eV,ne= 5 × 1010—6 × 1011cm–3.误差引入方案为对所选的16 条谱线涉及的15 个谱线上能级, 使用–30%—30%范围内的60 个随机数作为相对偏差, 引入每个上能级对应的截面数据.以上述2397 种Te-ne组合作为碰撞辐射模型输入参数, 配合900 种误差引入方案, 形成包含2397 × 900 组数据的光谱数据集, 用于训练神经网络. 考虑到光谱向量向等离子体参数的映射属于回归问题, 本文使用均方误差作为损失函数.图5所示的是使用两种数据正规化方法和两种神经网络结构时, 神经网络的训练情况.图中纵坐标表示训练时的均方误差, 由每步迭代中的网络输出值与训练目标值作均方差得到.由图5 可见, 在本文所选网络结构和正规化方法中, 双隐层网络结构搭配比和正规化方法有最快的收敛速度和最小的残差. 图6 所示的是电子温度和电子密度的训练目标和神经网络预测结果的对应关系.可以看出, 无论是对训练集还是测试集, 使用双隐层网络搭配比和正规化方法训练得到的网络都可以较好地预测电子温度和密度信息.网络预测结果在电子温度5—7 eV, 电子密度1 × 1011—3 × 1011cm–3的参数范围内误差较大, 不过整体上Te的预测结果与目标值间偏差均小于1%,ne的网络预测结果与目标值误差均小于3%.在5.3 节对神经网络诊断方法和最小二乘诊断方法的对比分析中, 使用双隐层网络结构搭配比和正规化方法训练的网络进行讨论. 首先就基础数据偏差对最小二乘方法的影响进行探讨.这里使用未含偏差的碰撞辐射模型生成待测光谱, 使用带有偏差的模型对其进行最小二乘拟合, 模拟实际诊断中基础数据存在偏差的情形,以揭示模型所使用基础数据上存在的偏差对最小二乘诊断方法的影响.进行最小二乘拟合时, 电子温度和电子密度作为拟合参数, 其他等离子体参数设置为与生成待测光谱时相同的值. 图7 所示的是在向氙等离子体光谱诊断中经常使用的881.941 nm 谱线对应的上能级的截面数据中分别引入5%, 15%和30%的偏差时, 待测光谱与使用最小二乘方法得到的最佳拟合的对比.生成图中待测光谱的参数设定值为电子温度=7.5 eV, 电子密度= 2 × 1011cm–3. 图5 使用不同网络结构和数据正规化方法获得的均方误差随迭代次数的变化Fig.5.Variation of mean square error with the number of iterations using different network structures and data normalization methods. 图6 网络预测结果与训练目标的对应关系 (a)电子温度的对应关系; (b)电子密度的对应关系; (c)电子温度的预测误差;(d)电子密度的预测误差Fig.6.Corresponding relationship between the network prediction result and the training target: (a) Corresponding relationship of the electron temperature; (b) corresponding relationship of the electron density; (c) prediction error of the electron temperature;(d) prediction error of the electron density. 图7 使用最小二乘方法获得的拟合结果(为保证图的可读性, 对离子谱线强度进行了放大处理, 并将拟合所得光谱的波长进行了偏置)Fig.7.Fitting results obtained by the least square method (in order to improve the readability of the image, the intensity of the ion spectral line is amplified, and a bias is introduced into the wavelength of the fitting spectrum). 图7 (a)是向拟合使用的模型中引入5%的偏差时, 待测光谱与光谱的对比情况.图中蓝色谱线为使用设定参数和代入模型生成的待测光谱;红色谱线为使用最小二乘拟合得到的最佳拟合光谱.图7(d)中红圈所示的是引入5%偏差时拟合结果与待测光谱谱线归一化强度的比值.可以看出此时谱线拟合的最大残差为3%; 诊断结果为电子温度Te= 7.4 eV, 电子密度ne= 1.9 × 1011cm–3.图7(b)和图7(e)为向拟合所用模型引入15%偏差时的结果, 此时谱线拟合的最大残差为9%; 诊断结果为电子温度Te= 7.2 eV, 电子密度ne=1.8 × 1011cm–3.图7(c)和图7(f)是向拟合所用模型引入30%偏差时的结果, 此时谱线拟合的最大残差为22%; 诊断结果为电子温度Te= 7 eV, 电子密度ne= 1.5 × 1011cm–3. 可见, 基础数据所含偏差导致最小二乘方法的拟合存在残差, 并使得诊断结果与参数设定值间产生偏差.基础数据的偏差大小与最小二乘方法的拟合残差和诊断结果偏差大小呈正相关.从上述例子还可以发现, 向一条谱线引入的偏差会导致所有谱线的拟合结果存在残差.这是最小二乘方法的特性使然: 由于等离子体中各种物理反应过程的强耦合作用, 寻找所有谱线均方误差最小的过程, 会导致单条谱线的偏差向其他谱线传递.导致实践中难以锁定偏差的根源来自哪些谱线, 无法通过实验获得恰当的调整因子.这正是使用调整因子方法进行光谱诊断的困难. 之后通过对比两种光谱诊断方法的误差半径和偏心距, 对两种方法的误差特性进行比较.在本文所研究的参数范围内, 选择Te和ne各11 个值作为设定值使用碰撞辐射模型生成待测光谱数据.对这11 × 11 个Te-ne组合的每个点, 使用一组均匀分布在–30%—30%间的60 个随机数作为偏差值, 依次作用于碰撞辐射模型中的15 个能级截面,得到包含121 × 15 × 60 组待测光谱的数据集.对于这组待测光谱, 分别使用基于最小二乘拟合和神经网络的诊断方法得到诊断结果.使用4.3 节中定义的误差半径和偏心距, 对最小二乘诊断方法和神经网络诊断方法得到的结果进行评价. 图8 (a)最小二乘方法诊断结果的平均误差半径; (b) 神经网络方法诊断结果的平均误差半径Fig.8.(a) Average error radius of the diagnosis result of the least square method; (b) average error radius of the diagnosis result of the neural network method. 图9 (a)最小二乘方法诊断结果的最大误差半径; (b) 神经网络方法诊断结果的最大误差半径Fig.9.(a) The maximum error radius of the diagnosis result of the least square method; (b) the maximum error radius of the diagnosis result of the neural network method. 图10 (a)最小二乘方法结果的偏心距; (b) 神经网络方法结果的偏心距Fig.10.(a) Eccentricity of the diagnosis result of the least square method; (b) the eccentricity of the diagnosis result of the neural network method. 图8 和图9 分别给出两种诊断方法诊断结果的平均误差半径和最大误差半径.图10 所示的是两种诊断方法诊断结果的偏心距.可以看出, 在本文讨论的参数范围内, 最小二乘方法诊断结果的平均误差半径在0.60%—15.88%之间, 最大误差半径在1.0%—26.70%之间, 偏心距在0.0007%—0.28%之间; 而神经网络方法诊断结果的平均误差半径在0.06%—0.71%之间, 最大误差半径在0.31%—2.08%之间, 偏心距在0.05%—0.79%之间.总体上, 神经网络诊断方法结果的误差半径明显小于最小二乘方法获得的误差半径; 在偏心距方面, 神经网络方法获得的结果与最小二乘方法基本相当, 两种方法获得的偏心距均在1%以下. 在本文讨论的等离子体参数空间内, 两种方法获得的误差半径和偏心距的分布有所不同.对于最小二乘诊断方法, 在电子密度高于1011cm–3时, 诊断结果的误差半径和偏心距普遍比电子密度低于1011cm–3时大; 而神经网络诊断方法获得的误差半径和偏心距分布较为平缓, 呈现中间高两边低的分布特性. 可见, 截面数据上的偏差向诊断结果的传递量的大小与电子温度密度参数范围也有关系, 这可能是由不同参数条件下, 等离子体中各种动力学过程此消彼长导致的: 被引入截面偏差的过程在激发态粒子产生或损失中的占比会随着等离子体参数的变化而改变.当被引入截面偏差的过程在激发态产生或损失中占据主导地位时, 截面数据上的偏差便会对激发态密度产生更大的影响, 进而导致最终的诊断结果出现更大的偏差.以后的工作中还将针对这一问题开展更深入的研究. 本节对神经网络和最小二乘两种光谱诊断方法解算实验采集的光谱数据的性能进行比较.图11所示的是两种光谱诊断方法获得的电子密度和电子温度与朗缪尔探针所得结果的对比.图11(a)和图11(b)分别给出了电子密度和电子温度的对比结果.图11(c)和图11(d)分别给出了两种光谱方法获得的电子密度和电子温度相对于朗缪尔探针所得结果的误差.可以看出, 整体上, 电离室内电子密度随着测点位置远离阴极, 呈现逐渐下降的趋势.这是由于随着测点远离阴极, 阴极发射的电子沿电离室径向逐渐扩散, 轴线上的电子密度因而逐渐减小.受到电离室内会切型磁场的影响, 电子在磁尖端附近存在一定的聚集效应, 导致6 号位置处电子密度有所抬升. 同时, 由于电离室筒形的阳极结构, 电场沿电离室轴线远离阴极的方向逐渐减弱, 电子获能随之变差, 导致电子温度随着测点远离阴极位置呈减小的趋势.由图10(c)和图10(d)可以看出, 在解算实验光谱时, 神经网络方法的误差均小于最小二乘方法.神经网络方法获得的结果相对于朗缪尔探针所获结果的误差不超过5%, 而最小二乘方法在部分测点处的误差超过了50%. 图11 (a)考夫曼离子源中电子密度的诊断结果; (b)考夫曼离子源中电子温度的诊断结果; (c)最小二乘方法和神经网络方法获得的电子密度结果的相对误差; (d)最小二乘方法和神经网络方法获得的电子温度结果的相对误差.“探针”、“最小二乘”和“神经网络”分别表示由朗缪尔探针、最小二乘方法和神经网络方法获得的诊断结果Fig.11.(a) Diagnostic results of ne in Kaufman ion source; (b) diagnostic results of Te in Kaufman ion source; (c) relative error of ne by least-square method and neural network method; (d) relative error of Te by least-square method and neural network method.“探针”, “最小二乘”, “神经网络” denotes the diagnostic results obtained by Langmuir probe, least-square diagnostic method and neural network diagnostic method, respectively. 从本文的研究结果可以发现: 1)由于等离子体中各种物理反应过程众多, 相互耦合作用强, 最小二乘法会使截面数据偏差在不同谱线间传递, 导致无法从拟合光谱与待测光谱得到的误差向量中锁定误差的来源.这给利用调整因子修正模型的方法带来了困难.2)神经网络方法能够辨识等离子体发射光谱的特征, 进而减弱部分谱线存在的偏差对整体诊断结果的影响.从本文的研究结果来看,截面数据偏差向诊断结果的传递量平均可由最小二乘方法的70%减小至神经网络方法的7%, 即神经网络方法可以减少60%以上的误差传递量.3)本文基于前馈神经网络开发的诊断方法能够对抗截面数据上存在的偏差.从5.3 节中两种诊断方法解算实验光谱数据的结果对比来看, 神经网络诊断方法所得结果的误差明显小于最小二乘拟合方法. 神经网络方法不仅可用于电子温度密度的诊断, 在利用分子转动谱测量气体温度、使用绝对光强方法测量激发态密度等问题的求解中同样具有良好的应用前景.此外, 使用神经网络方法分析等离子体发射光谱所消耗的时间要远小于基于最小二乘拟合的光谱诊断方法, 能够实时在线处理光谱数据.使其在刻蚀、材料处理等的等离子体加工工艺流程, 以及空间等离子体装置工作时对等离子体参数的在线监测上也具有良好的应用前景. 本文基于前馈神经网络发展了新的等离子体光谱诊断方法.通过对比新方法和以往常用的基于最小二乘拟合的诊断方法在截面数据存在偏差时的误差特性, 发现神经网络诊断方法在对抗基础数据偏差方面有更好的性能.对实验测量光谱的解算结果也证实了神经网络方法在这方面具有的优势.这种诊断方法在气体温度、激发态密度测量中具有较好的应用前景, 还可推广到等离子体刻蚀、材料处理等工艺流程的等离子体参数的在线监测中, 有望进一步提高测量的实时性和监测精度. 感谢Maxime Bezanilla 先生对本文工作的启发.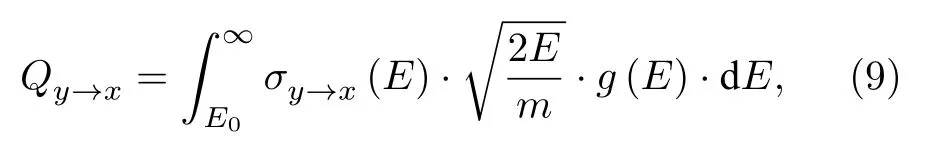
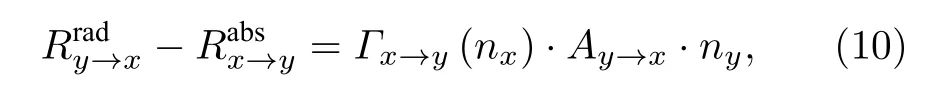
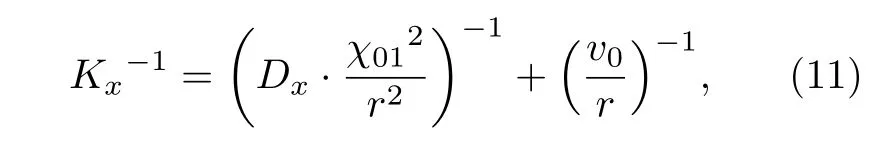
3 诊断实验
4 数据分析方法
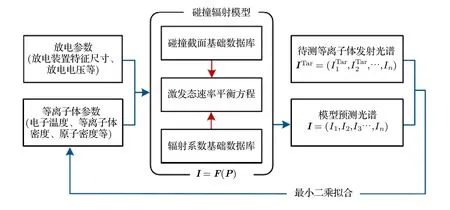
4.1 基于最小二乘拟合的光谱诊断方法

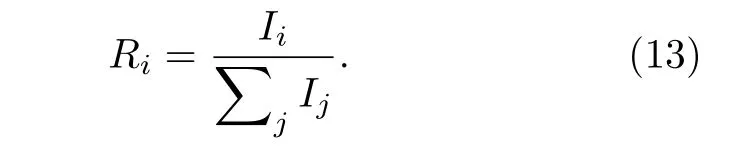
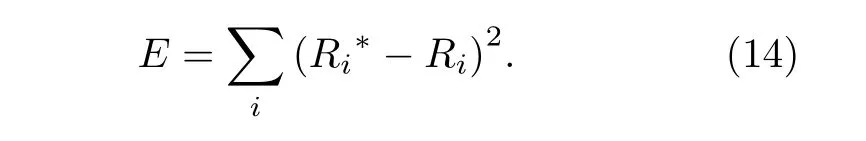
4.2 基于前馈神经网络的光谱诊断方法
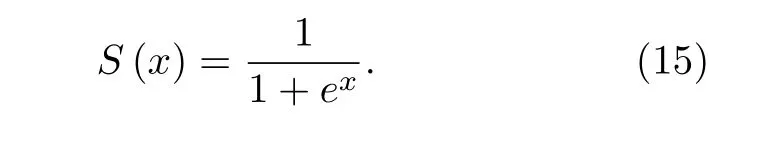
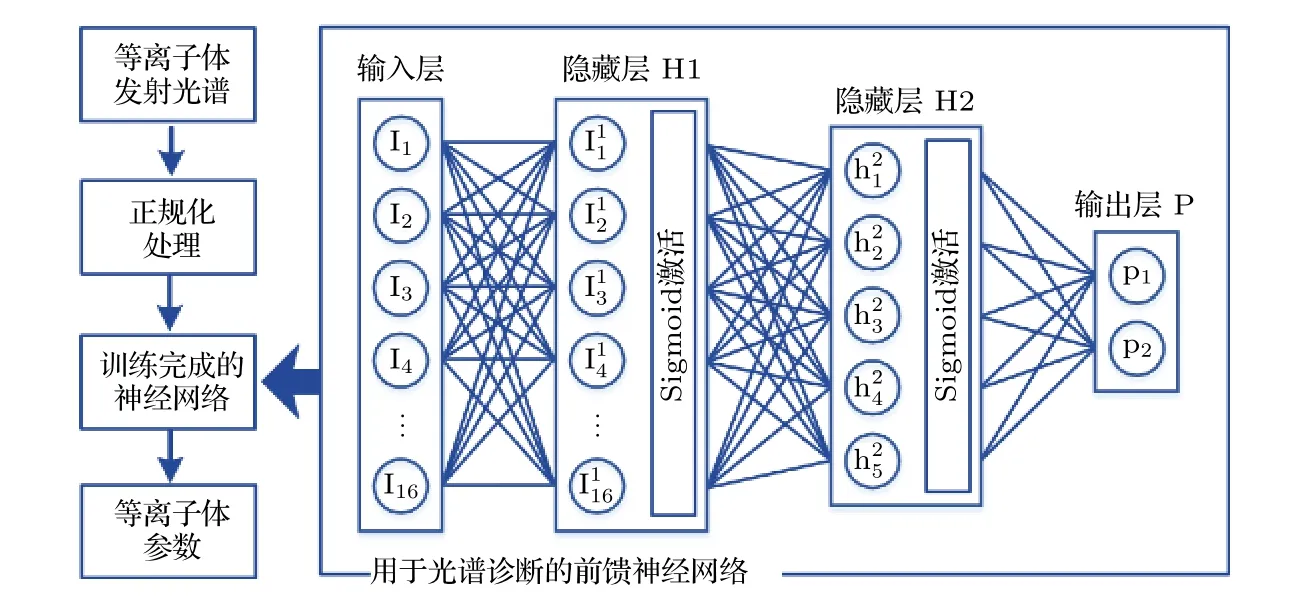
4.3 诊断方法的比较

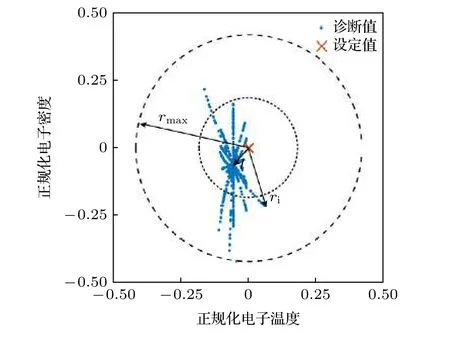
5 结果与讨论
5.1 神经网络训练及验证
5.2 最小二乘诊断方法和神经网络诊断方法误差特性的对比
5.3 诊断方法的考核实验
6 结 论
