基于Elman神经网络的信号降噪方法研究

（沈阳理工大学装备工程学院 辽宁·沈阳 110159）

0 引言

雷达工作环境具有开放性和复杂性，由于工作环境及雷达系统元器件等诸多因素的影响，其回波信号中往往伴随着杂波噪声和热噪声等多种噪声干扰。因此，对雷达回波信号降噪技术的研究已成为信号处理领域及军事领域的热点问题。针对雷达回波信号的传统降噪方式主要是基于傅里叶变换的思想，通过频域滤波来实现。传统算法需要预先知道雷达回波信号的具体频谱特征，这大大限制了传统算法在雷达回波信号降噪中的应用。神经网络技术具有自我学习、自行组织、平行处理的特点，能够实现对无法预知信号的降噪处理。Elman神经网络是一种典型的动态递归神经网络，它是在BP神经网络的基础上，在隐含层增加一个关联层，作为延时算子，达到记忆的目的。因此，Elman神经网络具有适应时变特性的能力，其网络全局稳定性更强，与前馈型神经网络相比，Elman神经网络具有更强的降噪精度。

本文通过分析Elman神经网络结构的特点，构建了Elman神经网络降噪模型，并利用该模型对连续波回波信号和方波回波信号进行网络训练和降噪仿真。仿真结果表明Elman神经网络对雷达回波信号降噪效果明显。

1 Elman神经网络降噪模型

Elman神经网络是应用较为广泛的一种典型的反馈型神经网络模型，包含输入层、隐含层、关联层和输出层。关联层用来记忆隐含层单元前一时刻的输出值，隐含层的输出通过关联层的延迟与存储，自联到隐含层的输入，这种自联方式使Elman神经网络对历史数据具有敏感性，内部反馈网络的加入增加了网络本身处理动态信息的能力，从而达到动态建模的目的。关联层中的神经元具有的都是线性函数，它接收到隐含层的反馈信号后会记住前一时刻的输出值，然后会经过一段储存与延迟的时间，这样能让整个神经网络可以很好的适应时变的特性，并增强神经网络处理动态信息和整体稳定性的能力。构建单输入单输出的Elman神经网络降噪模型如图1所示。

令u(i)为输入的雷达回波信号，x(i)为 Elman神经网络隐含层神经元信号，y(i)为输出神经元信号，w1为关联层到隐含层的连接权值；w2为输入层到隐含层的连接权值；w3为隐含层到输出层的连接权值，d(i)为期望输出的雷达回波信号，为误差函数。则有：

2 Elman神经网络模拟训练

基于所建立的Elman神经神经网络降噪模型，分别将连续波回波信号、方波回波信号及其目标信号作为样本，对该非线性网络进行模拟训练，直至网络性能达到最小误差阈值10-5。其他训练参数设置如下：训练次数为 103次，学习速率为5×10-2，最小性能梯度为10-6，最大确认失败次数为5，动量因子为0.95。连续波回波信号和方波回波信号的Elman神经网络模拟训练误差分别如图2和图3所示。

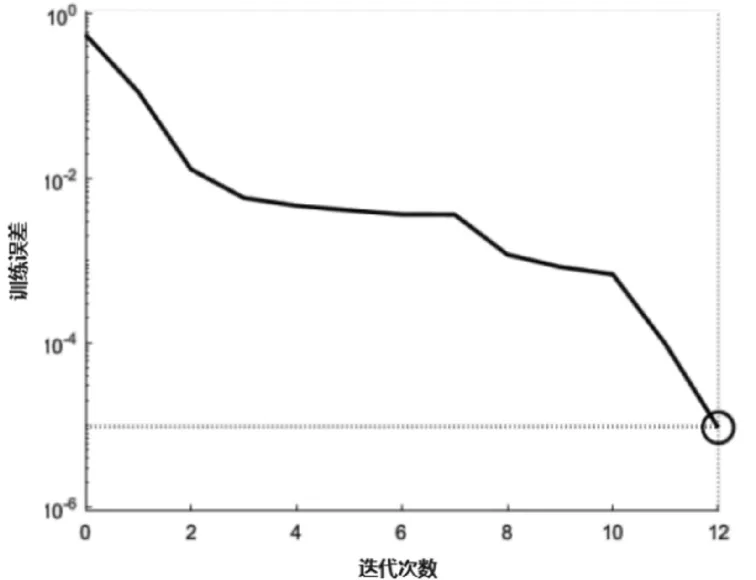
图2：连续波模拟训练误差

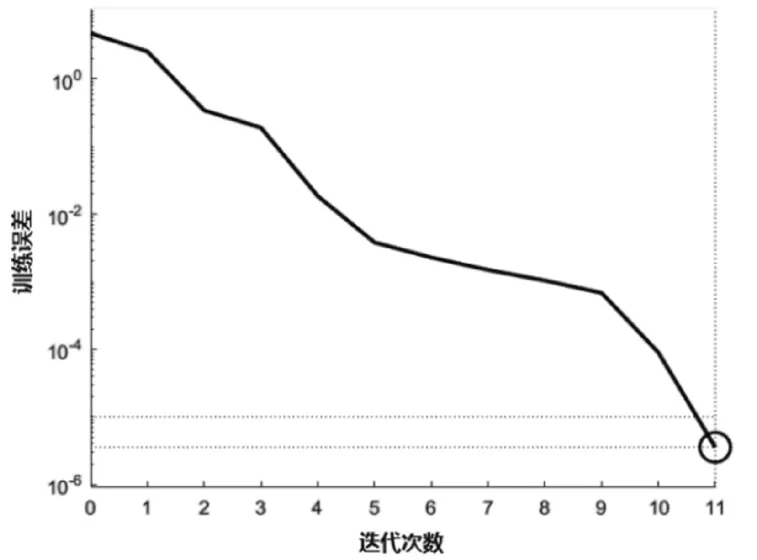
图3：方波模拟训练误差

由图2和图3可以看出，分别经过12次迭代训练和11次迭代训练，Elman神经网络性能即能够达到设定的最小误差阈值10-5。训练结果表明，所设计的Elman神经网络降噪模型可以很好的模拟出连续波回波信号降噪系统和方波回波信号降噪系统。但实际应用中应注意，最小误差阈值的变化将改变迭代次数的大小，而过小的阈值可能导致Elman神经网络无法正常训练。因此，在实际应用中要根据不同雷达的性能指标设定合适的最小误差阈值。

3 雷达回波信号降噪仿真

降噪前的连续波回波信号如图4所示，将该湮没在噪声中的连续波回波信号输入到训练后的Elman神经网络进行降噪处理，降噪结果如图5所示。

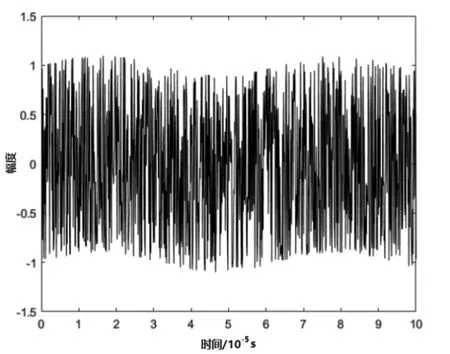
图4：湮没在噪声中的连续波回波信号

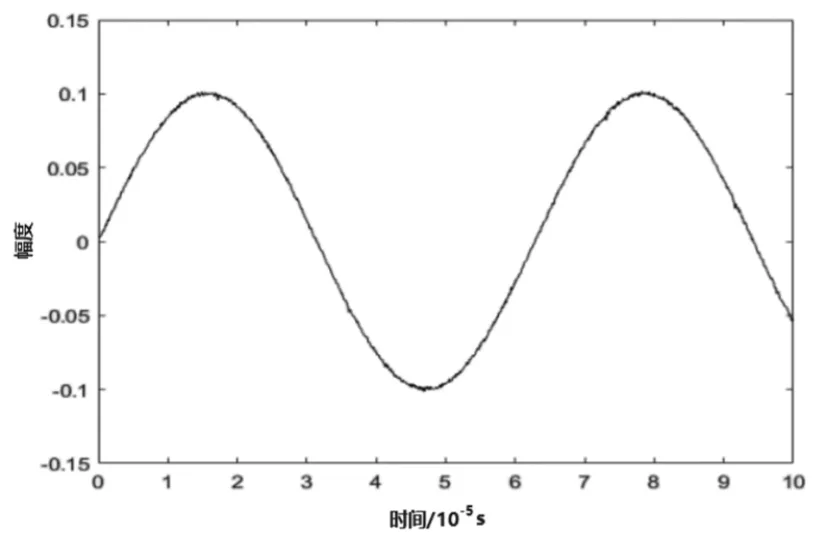
图5：Elman神经网络降噪后的连续波回波信号

由图5可以看出，降噪后的输出波形能够很好的拟合理想输出波形，其降噪后的输出波形平整均匀，毛刺较少。显然，本文设计的Elman神经网络对连续波回波信号有明显的降噪效果。

将方波回波信号输入到训练后的Elman神经网络进行降噪处理，降噪结果如图6所示。

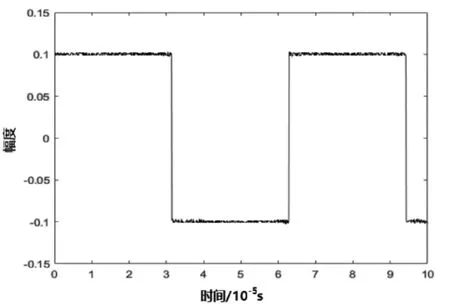
图6：Elman神经网络降噪后的方波回波信号

由图6可以看出，Elman神经网络对方波回波信号同样具有明显的降噪效果，降噪后的方波波形毛刺较少。

将上述连续波回波信号和方波回波信号输入到训练后的Bp神经网络进行降噪处理，其降噪结果分别如图7和图8所示。

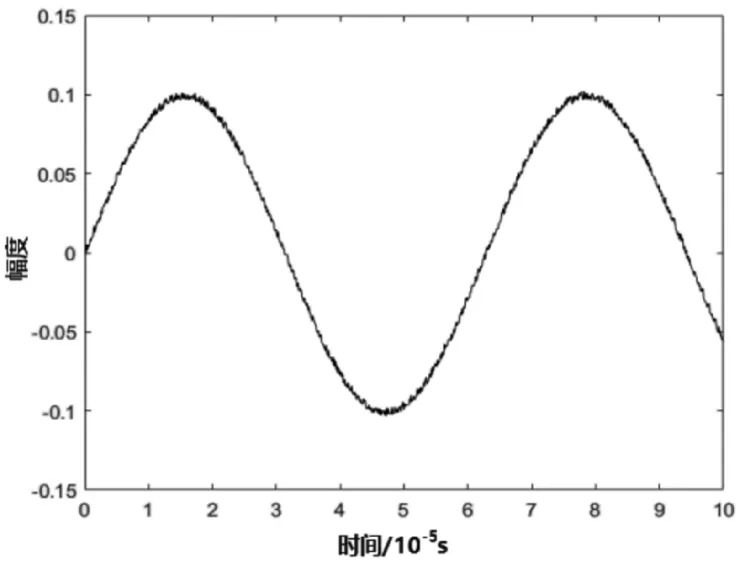
图7：Bp神经网络降噪后的连续波回波信号

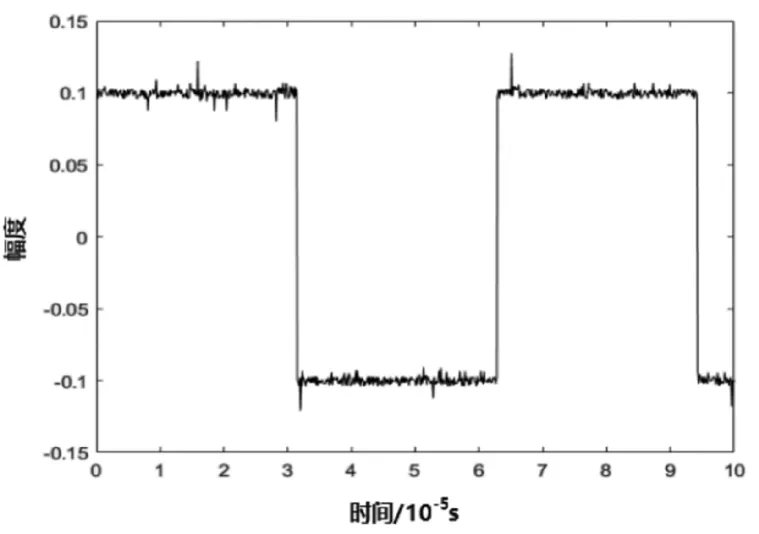
图8：Bp神经网络降噪后的方波回波信号

显然，与传统的Bp神经网络相比，本文设计的Elman神经网络对雷达回波信号降噪效果更优。

4 结论

雷达回波信号的降噪处理对提高雷达的探测识别性能至关重要。因此，本文在研究了Elman神经网络结构的基础上，建立了Elman神经网络降噪模型，并通过仿真验证了Elman神经网络对连续波回波信号和方波回波信号的降噪效果优于传统的Bp神经网络。