把握周长中的“变”与“不变”——小学数学“一图一课”备课模式课例分享

（深圳宝安区西乡街道径贝小学 广东·深圳 518102）

1 “一图一课”备课图

2 教学环节剖析

环节一：认识2×3的长方形

师：黄老师这里有一个比较特殊的长方形，它是由6个边长为1的正方形片拼成的，它的周长是几？给出你的算式。

（学生上来后，引导学生先“摸”出这个长方形的周长在哪里？）

生1：3×2 ＋ 2×2

生2：（2 ＋ 3）×2（长方形的周长公式）

生3：2＋ 3＋2＋ 3

环节剖析：在此环节中，有两个小细节的处理特别关键，一是在学生上后，教师要引导学生先“摸”出这个长方形的周长在哪里？明确里面的边都不算作周长；二是让学生结合图形说出算式！算式在一定程度能比较直接地反映出学生计算该图形周长的思路，如生1的思路就是长长＋宽宽，生2的思路就是（长＋宽）×2。

环节二：为了维持周长不变，我们可以拆走哪一片？

【示范拆走①号】：

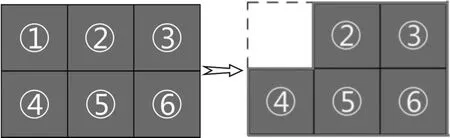
在此环节中，我首先示范拆走①号，然后让学生看着图形讨论大概20秒—“拆走了①号，和原来的长方形相比，周长变了吗？”

（学生上来后，引导学生先摸出拆了①号后的图形，它的周长在哪里？）

生1：我认为周长没有变，因为拆了①号后，不见了这两条边，但是这里又多出两条边（指着图形解释），所以周长还是10；

生2：我认为周长不变，因为拆了①号后，这条边移到这里，这条边移到这里（指着图形解释），还是原来的长方形；

师（总结）：黄老师想用四个字来归纳大家的想法，“少2补2”（板书），你能看得懂吗？结合图形说说！

环节剖析：在此环节中，要明确拆了①号后的图形，它的周长在哪里？让学生结合图形分享自己的想法！引导学生关注“拆走几条边？又补回来几条边？”给予学生一种表述的方法，即“少（ ）补（ ）”。

【自主探索其他拆法】：

为了维持周长不变，我们可以拆走哪一片？

学生通过操作学具以及小组合作，绝大部分都能找到全部的拆法（①、③、④、⑥），因此在分享环节中，不需要一一让学生上来说每一种拆法，因为经过前面的示范，学生基本都能用“少2补2”来解释“为什么周长不变！”我个人会抛出以下两个问题：

问题一：这四个图形的形状有什么联系？

生1：这四个图形的形状是一样的，只不过有些是“调过来”的；

生2：它们拆的都是“角”。

环节剖析：学生的发现其实是逐步深入的，当有学生发现形状都是一样时，也就会指向拆的都是长方形的一个角！这时，教师可以追问“为什么拆四个角，周长不变？”，引导学生发现拆四个角的共同特征就是“少2补2”。

问题二：为什么不能拆中间的②号或⑤号？（结合图形分享想法）

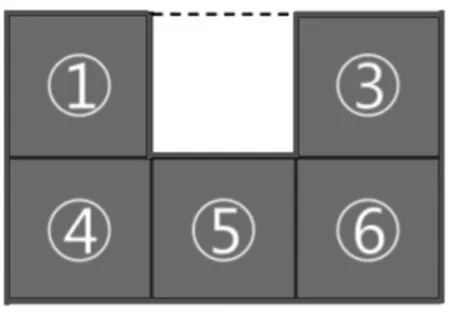
生1：拆去②号或⑤号，少了这条边，但是这里多出了3条边，所以周长变为了12，周长变了。

师：如果用四个字归纳，应该怎么说？

生1：少 1 补 3！

环节剖析：这节课的课题是《周长变了吗？》，那必须指向两个方面，即：周长变了和周长没变！因此，要重点让学生结合图形分析：为什么不可以拆中间的②号或⑤号，因为“少1补3”，周长变了！

环节三：已经拆走了①号，还可以再拆走哪一片？

【操作前的思考】：

师：先不动学具，小组看着图形讨论一下，还能再拆走哪一片？

（1min左右）

生1：我觉得还可以拆走③号或者⑥号，因为...

生2：我觉得②号也可以拆，因为...

环节剖析：有了拆一片的经验——拆四个角！学生在考虑再拆一片的时候，一般会优先考虑“角”，即③、④、⑥号，然后用“少2补2”排除④号。那②号呢？在拆一片时是不可以拆中间的②号或⑤号，那拆去两片时，②号到底可不可以呢？

此环节，教师可放开让学生说出他的想法，但不必引导说的太清楚，毕竟学生还要动手验证，还有机会通过自己的努力摸清其中的奥秘！

【操作、讨论、分享】：

这里，我会让学生关注三个问题：

问题一：如果把①号和③号看作是一起拆走的，那是少（ ）补（ ）？

生1：少 4 补 4（①③/①⑥）。

问题二：拆两片时为什么可以拆中间的②号？（这是上课时，一个小女孩提出的问题，当时我没有做预设，于是把问题抛给学生解决。）

生1：因为拆①号是“少2补2”，再接着拆②号也是“少2补2”，所以中间的②号可以拆。

生2：因为同时拆去①②号就是“少3补3”周长不变！（这是之后的课里，我抛出这个问题时，学生的回答）。

问题三：为什么不能拆①④号？谁能结合图形说说！

生1：把④号拆走，那是“少3补1”，这是不可以的！（从再拆一个的角度分析）。

生2：我们看作同时拆走①④号，那就是“少4补2”（已经学会了整体分析了。）

环节剖析：在分享的环节，引导学生关注“两片同时拆走”，从之前单一的“少2补2”扩展到“少4补4”、“少3补3”、“少4补2”等等。最后带着学生一起总结—少几补几，则周长不变！

环节四：要使周长不变，最多可以拆掉几块正方形片？

【探索前的猜想与验证】：

学生有了前面的学习，会马上联想到“角”，可以拆掉四个角（少8补8），因此周长不变！但是也有的同学“脑洞”比较大，认为最多可以拆掉5块，四个角＋中间的⑤号（首先这在学具上是实现不了的，其次，拆了中间的⑤号，那就是“少0补4”了）。

面对学生的猜想，我想以一种“参与感”很强的方式来进行验证，即依次抽一名同学，让该同学“建议”黄老师拆去哪一片？而学生一般会按照：①③⑦⑨的方法进行“建议”。当然，也一定会有其他的方法，只要学生明白“少几补几”的号即可拆去。

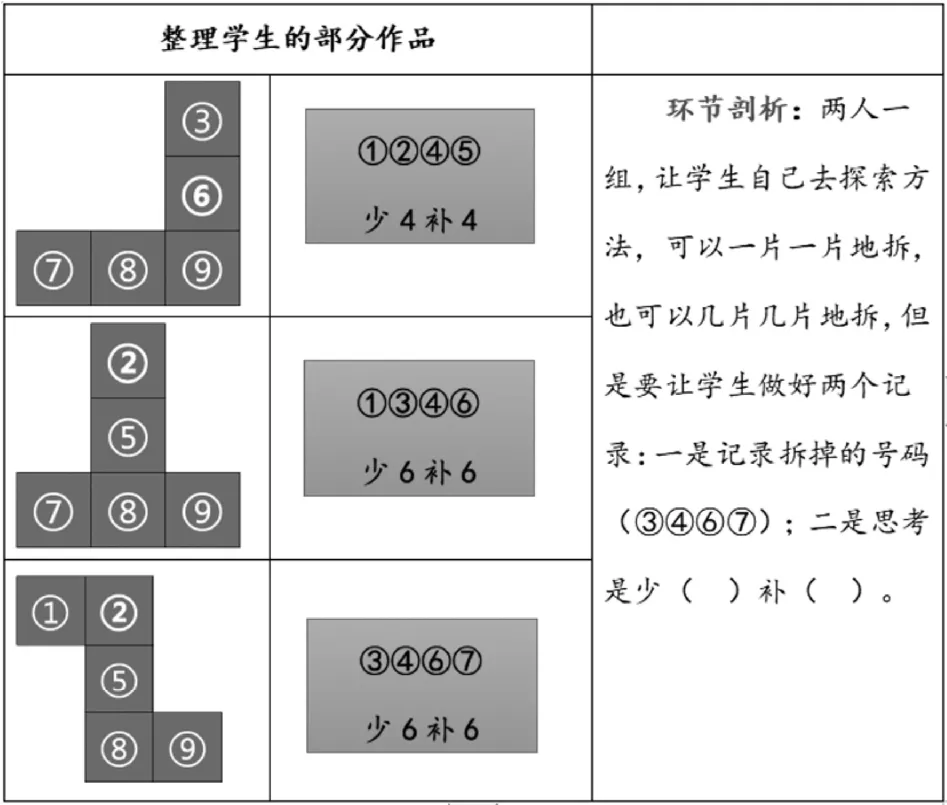
【探索拆去四片的其他方法】：

整理学生的部分作品。

环节剖析：两人一组，让学生自己去探索方法，可以一片一片地拆，也可以几片几片地拆，但是要让学生做好两个记录：一是记录拆掉的号码（③④⑥⑦）；二是思考是少（ ）补（ ）。