动力学中功和能综合分析

赵诗华 朱 琴 艾 茜

（[1]中国矿业大学（北京）理学院 北京 100083；[2]北京市昌平区第二中学 北京 102208）

功和能都是标量函数，对应的规律如动能定理、机械能守恒定律等等是标量函数方程。所以从功和能的角度上解决动力学问题是常用的重要方法。动力学中的功和能内容是物理教学的重点之一，本文对动力学中功和能问题做一综合分析，并举例解析。

1 定义

1.1 功

1.2 功率

作用在物体上的力在单位时间内做的功称为功率，即

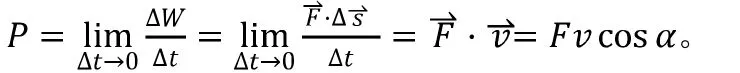
1.3 动能

1.4 保守力、非保守力、势能函数

做功与路径无关的力称为保守力，做功与路径有关的力称为非保守力．在数学上为了描述保守力做功与路径无关的特性引入的函数称为该保守力的势能函数。

常见的保守力有四种：万有引力，重力（万有引力的分力，一般单独为一种力），弹簧弹性力，电场力。常见的非保守力有两种：摩擦力，安培力（洛伦兹力永不做功）。

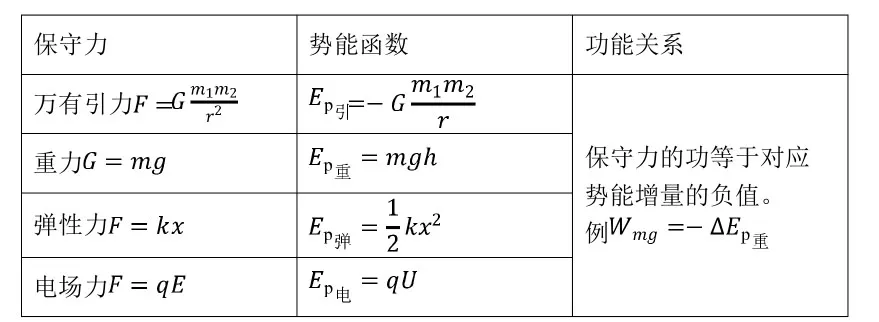
保守力 势能函数 功能关系万有引力重力弹性力保守力的功等于对应势能增量的负值。例电场力

2 求功的方法

2.1 按定义求功

2.2 由功能关系求功

（1）动能定理：

①质点动能定理：质点所受外力做功代数和等于质点动能的增量，即

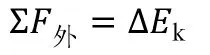
②质点系动能定理（由质点动能定理推得）：作用于质点系所有外力做功之和加上所有内力做功之和等于质点系总动能的增量，即

动能定理解题见例1。

（2）机械能守恒定律：在只有重力或弹力做功的系统内，动能与势能相互转化，总的机械能恒定不变。即

（3）在只有重力、弹力、电场力做功的系统内，动能、重力势能、弹性势能、电势能相互转化，总能保持不变，即（见例2）。

（4）热力学第一定律：一个热力学系统的内能增量等于外界向它传递的热量与外界对它所做功的和，即。

（5）伯努利方程：作定常流动的液体中，在同一流管中任何一点处，流体每单位体积的动能和势能以及该点压强之和是个常量，即。

（7）能量守恒定律：能量既不会消灭，也不会创生，它只会从一种形式转化为其它形式，或者从一个物体转移到另一个物体，而在转化和转移的过程中，能量的总量保持不变。

实际上功能关系求功中前6种求功的方法，都是能量守恒定律的特例。

2.3 图像法求功（见例3和例4）

2.4 微元法求功（见例5）

图1

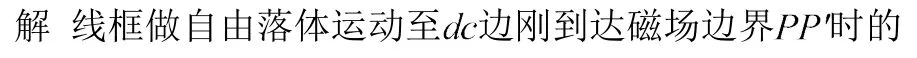
图2

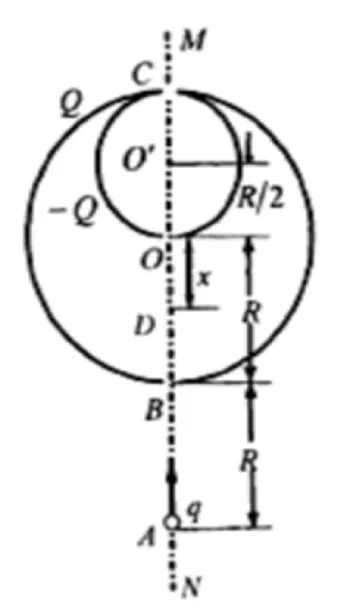
图3

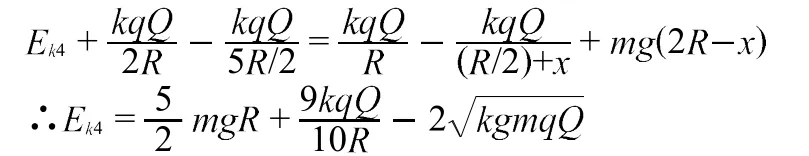
例3跳水运动员从高于水面H=10m的跳台自由落下。设运动员质量m=60kg，其体形可等效为一长度L=1.0m，直径d=0.30m的圆柱体。略去空气阻力，运动员入水后，水的等效阻力F作用于圆柱体的下端面。F的量值随水的深度 变化的函数曲线如图4所示。该曲线可近似看作椭圆的一部分，该椭圆的长、短轴分别与坐标轴OY和OF重合。椭圆与Y轴相交于Y=h处，与F轴交于F=5mg/2处。为了确保运动员的安全，计算水池中水的深度h至少应等于多少？（水的密度ρ=1.0×103kg/m3）

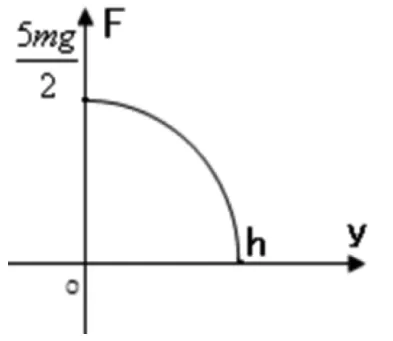
图4

解 如图5，根据受力不同，把运动员直线运动分为三个过程。

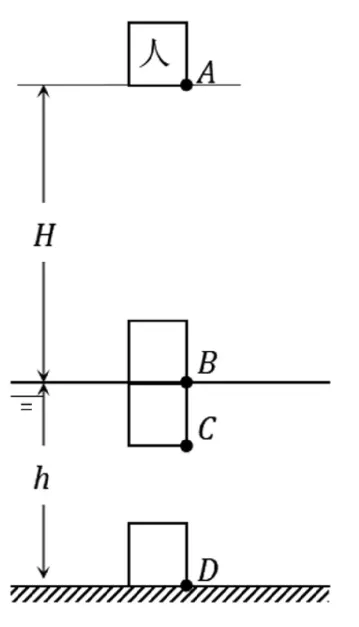
图5

（1）A→B自由落体运动，只受重力作用，重力做功。

（2）B→C减速运动，刚浸入水到完全浸入水中，受重力mg、浮力f1、阻力F作用，三力均做功。

（3）C→D减速运动，完全浸入水中到刚好速度为零时接触水池底面，受重力mg、浮力f2、阻力作用，三力均做功。

下面先求f1，如图6

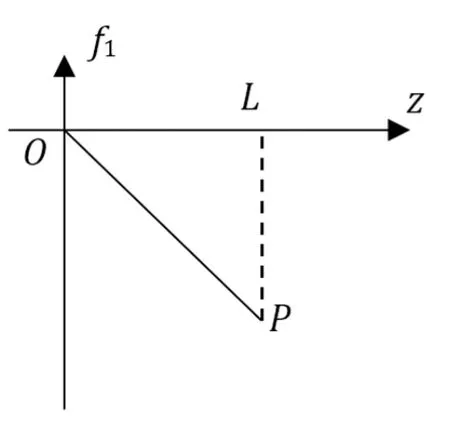
图6

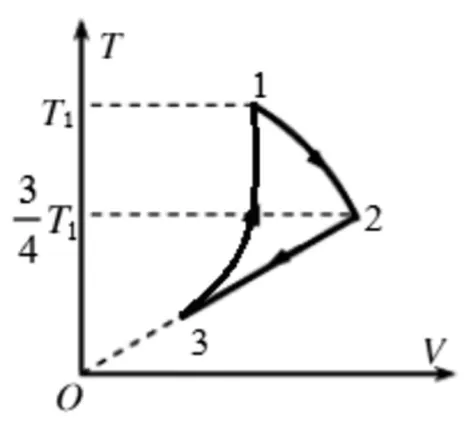
图7

在p-V图中画出循环过程1-2-3-1图线，如图8所示．气体在此循环过程中对外做正功，其值W等于△123的面积，即

图8

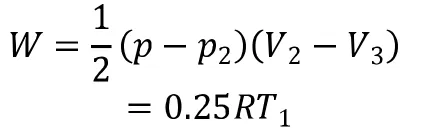
图9