试卷分析中主要分析指标的效用探讨

（空军航空大学航空作战勤务学院 吉林·长春 130022）

0 引言

考试是根据考核的目的，让考生在规定的时间内，按规定的方式，完成事先所编制的题目，并按解答的结果给予评分的过程。考试完毕后进行的试卷分析，是教学过程中的一个重要环节，是教学考核与评估中的内容之一。试卷分析就是在输入试卷基本信息及分析样本数据后，由计算机进行数据处理，直接输出分析及评价结果。通过结果，一方面相当于建立了教学系统中的信息反馈渠道，可以了解学生学习效果和教学中的薄弱环节，教师可以及时地调整和改进教学内容和方法，学生可以及时地加强薄弱环节的学习内容、改进学习方法。另一方面，根据结果可以发现试卷命题及组卷中的问题，对于试卷命题本身具有评价作用，客观反映出试卷命题的好坏，对于评价教学、规范命题等都具有现实指导意义。所以，进行试卷分析包含有两个方面的内容：试题质量分析和考试成绩分析。

1 试题质量分析

一般考试中最常见的是学业成就测验，它依据教育目标进行考试命题，命题水平的高低直接影响能否正确的评价学生的学习质量和教师的课堂教学水平。对于选拔考试来说，甚至于直接决定了能否客观公平的鉴定考生资格、筛选人才。进行客观的试题质量分析是试卷分析的必要环节，也是教育教学评价的重要内容之一。试题质量分析包含以下若干内容：

1.1 一致性分析

试卷命题的一致性是命题的基本要求，它要求试题不偏离课程标准或考试大纲，符合对知识点的认知要求和学生素质能力培养要求，体现教学过程和方法，间接蕴含情感态度与价值观。通常可以从试卷上反应的测试内容、认知要求、价值取向等几方面考察命题一致性的质量。

命题一致性优秀的试卷有助于师生在教学中注重对于课程目标的明确，有目的的教学有助于教师教学中围绕课程标准，有的放矢，具有针对性；有目的的学习有助于学生学习积极性的调动，提高学习效率，事半功倍。

1.2 科学性分析

试卷命题的科学性，是指试题包含的知识点的分布合理性，包括知识点的覆盖度、题目难度分布，题型选择，题量大小等内容。一套科学性较好的考试试题，应该是课程标准中知识点的覆盖度高，并且是一个有机的整体。要根据试卷的知识点分布和对知识点要求掌握程度的高低，来合理分布单个试题的难度系数，不可机械的堆砌大量试题、更不能出现知识点和计算方法与计算技巧重复的现象。

命题科学性高的试卷更能公平、公正的反映学生的客观成绩，有助于客观衡量学生学习质量与反应教师教学水平。

反映科学性的一个分析指标就是信度。信度就是指试卷的可靠性和稳定性程度。由于试卷分析多用于期末测试，不可能重复测试，所以目前试卷分析多为计算内部一致性信度。内部一致性信度是同一试卷的两个部分，例如分为奇数题和偶数题，通过计算得分的相关程度。计算方法有分半法、库德理查森公式法及克龙巴赫所创的系数公式法。

1.3 有效性分析

试卷有效性分析是指试卷的准确性程度，它反映了测量结果与被测量的二者之间的符合程度，也就是指在命题组卷时选取的具有代表性的样本组成的考试内容，是否能够恰当的代表教学内容总体。有效性的评估有助于客观、真实的反应学生的整体学习水平，特别是在选拔考试中，准确度高的甄选出优秀可塑性人才。

实际上到目前为止，还没有一种切实可行的统计方法可以用来合理地评价试题取样的恰当程度。大多采取的办法是由有经验的老师或者专家依据考试大纲对每道试题进行比较分析来作出估计。或者采用通常效标关联效度来评估，也就是说用公认的比较客观的一次同类标准考试成绩来评估，两者之间的相关系数就是效标关联效度，具体计算可以采用积差相关法。

1.4 技术性分析

1.4.1 难度分析

难度分析指对试题的难易程度的分析，在经典教育测量理论中，通常采用通过率和平均得分率这两种办法。通过率的难度计算公式为P=M/N，M为对某题作出正确答案的考生数，N为参加测试的总人数。平均得分率的难度计算公式为P=X/W，X为全体被试者在某题上得分的平均值，M为该题的满分。

试题难度系数的大小可以根据命题人的意图进行确定和调整。难度系数一方面可以体现出试卷的指导思想，难度系数大可以严格控制高分数的出现，可抑制学生骄傲浮躁情绪出现；而难度系数小又可以让学生相对容易地得到较高分数，有鼓励学生增强自信心的作用。另一方面可以为筛选试题、确定难度建立试题题库做准备。

1.4.2 区分度分析

试题的区分度能充分体现学生的学习水平及应用知识的能力。区分度较好的试卷，学习能力强的学生实际得分就高，真实反映了学生的实际情况。试题的区分度是测验试题否具有效度的指标，用来评价试题质量、筛选试题。

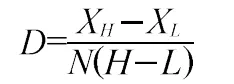
公式中，D为区分度指数，XH为高分组(总人数的25%)的得分总数，XL为低分组(总人数的25%)的得分总数，H为这试题或试卷的最高得分，L为这试题或试卷的最低得分，高分组人数与低分组人数相等，用N表示。

一般认为区分度大的为优秀试题，区分度较小试题较差，应进行适当的改进，区分度过小的为“劣题”，必须淘汰。通常难度系数和区分度是紧密联系，难度过高或过低都会降低区分度。要出一套完整合理而又科学的试题，就要充分考虑其难度系数和区分度。

2 考试成绩分析

如果试卷质量优良的基础上，对试卷成绩进行汇总分析，既有助于教与学的反馈轮回，在这其中教师可以不断改进教学方法，提高教学水平。分析考试成绩的常用的指标有平均成绩、正态分布、两极差、方差、标准差等，这些方法可以分为集中量和差异量两类。

2.1 用集中量进行分析

一个是利用平均成绩，平均成绩是这个学生集体考试成绩的平均分数，是该集体学习成绩集中趋势和典型水平的代表值，其计算公式为

其中，M为平均成绩，Xi为第i个学生的考试成绩，N为参加考试的学生人数。平均成绩反映了整体水平，例如一个班的整体水平，能够局部反映一个班的学习状况。

另一个指标是成绩的正态分布，如图所示。正态分布又称分布是数理统计学的一种很重要的连续型分布，正态分布的主要特征是对称性，以平均数为中心左右呈现对称。

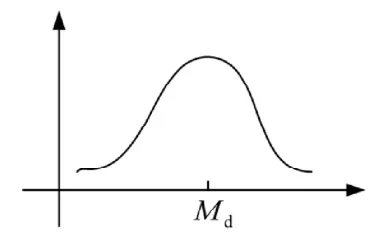
为了保证判断分布是否成正态分布的准确性，样本的抽取应该尽量多。如果样本呈现正态分布，能够发现学习优异生和特困生，可以在在教学过程中给予特殊关照。如果样本不服从正态分布，例如呈现偏态分布或多峰分布，则需做相应的深入分析。如果分布曲线高峰向左偏，则反映低分较多，平均分较低，试题偏难。如果曲线高峰向右偏，则反映高分较多，平均分较高，试题偏简单。如果学生学习情况两极分化情况严重，试卷会出现成绩分布畸形的情况，如出现双峰值状态。

进一步还可以计算出样本的均值 X和方差 Sn2。其中 x为样本平均分，可以用来近似地表示全年级各学科的平均分。而Sn2反映了数据的分散情况，Sn2越大表示考试成绩的波动性较大，Sn2越小表示考试成绩的波动性较小。

2.2 用差异量进行分析

差异量通常有两极差R和标准差 来表示。

两极差R指最大数与最小数之差。考试成绩抽取的样本中的极差反映了最高成绩与最低成绩的差异，对这个差异的分析希望在排除偶然因素的情况下，可以具体追踪到个人，分析出现成绩低的原因，反馈指导以后的教学。

标准差 的计算公式为：

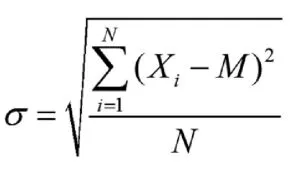
其中，M为平均成绩，Xi为第i个学生的考试成绩，N为参加考试的学生人数。

标准差反映了一组数据离散程度最常用的一种量化形式。例如两个期班的平均成绩可能一样，可是标准差并不一样，标准差越大，说明样本的离散程度越高，也就是说高分与低分的越多，两极分化越大。

3 试卷分析的主要分析指标应用

从收集到的大量文献分析看，目前试卷分析实践的理论基础还是基于经典教育测量理论为主，也就是试题的难度和区分度分析以及试卷的信度和效度分析。大量文献可以看出，许多高校在试卷分析研究与实践中仅针对难度、区分度和信度三个指标进行了有效性分析，效度由于其不容易采用有效的指标进行衡量，效标的选择是计算试卷效度的难点，所以很少见有涉及效度研究文献。

从文献中也发现，我国研究着开发的试卷分析系统多以Windows作为操作平台，包括Windows95/98/NT/2000/XP/7，前台开发工具包括面向对象的可视化程序设计语言VisualFoxPro、Delphi5.0、VisualBasic6.0等。后台采用的数据库包括Microsoft Access97/2000、FoxPro、Excel等。大部分系统功能单一，仅仅算是涉及到了试卷分析，只有部分系统功能强大，既包括试卷分析，还包括题库建设和维护，部分系统还增加考务分析等功能。单一系统工作范围十分局限，综合系统大都可在网上运行。

大多数高校的试卷分析仅仅出于经典理论框架下的应用探讨，虽然部分研究者在实践中对计算公式进行了优选和改进，但都没有取得太大突破。甚至于有些高校试卷分析研究还停留在手工统计，尚未利用计算机技术。可以看出关于试卷分析工作研究的任务很艰巨，急需大量人力物力的投入研究。

4 结论

通过综合试卷各项指标信息，对试卷质量进行定量化分析，从难度、区分度、信度和效度等方面进行研究，以便确定试卷结构是否合理。另外，通过分析试卷的应试结果，可以得到考生群体的成绩分布，用来评估学生对于知识的掌握和运用情况，诊断出学生在学习过程中遇到的疑难点，教师可以以此为依据进行相应的教学反馈，开展因材施教的个性化教学。目前许多高校对试卷分析的工作已逐渐加以重视，但是由于前期投入有限，急待大量工作者的研究并付诸于实践。