基于统计分布的近距平行跑道配对进近纵向碰撞风险评估
2021-05-14谢春生梁献匀
谢春生, 梁献匀, 卢 飞
(中国民航大学空中交通管理学院, 天津 300300)
近年来,由于民航业的迅猛发展,空中交通拥堵问题日渐突出。为缓解空中交通拥堵现状,在不扩建机场跑道的前提下,如何充分利用现有近距平行跑道成为民航领域的研究热点。研究配对进近为提高近距平行跑道的利用率提供了理论依据,也为中国繁忙机场早日实现近距平行跑道配对进近奠定了理论基础,具有强烈的现实意义。
针对近距平行跑道配对进近的研究目前虽尚处于发展阶段,但中外已有一定的相关研究成果。国外方面,Hammer[1]最先阐述了配对进近的想法;Landry等[2]探讨了配对进近的安全区域;Teo等[3]深入探究了配对进近的危险区域;Eftekari等[4]研究了前机尾流对配对进近的影响,并讨论了配对进近的可行性;Burnham等[5]进一步分析了在侧风条件下前机尾流对配对进近的影响。中国方面,胡明华等[6]总结了在机场近距平行跑道进近的方法;卢飞等[7-8]给出了评估配对进近纵向和侧向碰撞风险的模型;田勇等[9]求解了配对飞机的运行间隔;何昕等[10]研究了两种配对方式下的安全区域;谷润平等[11]描述了配对进近的过程,并计算了配对飞机在运行中的碰撞风险;卢飞等[12-13]构建了后机遭受前机尾流影响时的力矩平衡模型,从而确定了配对飞机的尾流安全区域。
在以往的研究中,建立碰撞风险评估模型时或是未研究实际数据的统计分布,直接假定飞机定位误差服从正态分布;或是未量化配对进近各个阶段的时间;或是未引入后机的侧向偏置进近程序。基于上述问题,先通过广播式自动相关监视(automatic dependent surveillance-broadcast, ADS-B)数据拟合出飞机纵向定位误差的统计分布;随后分为5个阶段研究配对进近的过程,量化配对进近各个阶段的时间,在后机侧向偏置进近的情形下,评估配对进近全程中飞机的纵向碰撞风险。
1 配对进近过程
配对进近是指在跑道中心线间距小于或者等于762 m的近距平行跑道上,在满足最小碰撞风险安全间隔的条件下,前机与后机建立各自的航向道后,在间隔足够小的情形下能够同时进行进近,依次完成着陆。
将配对进近过程分为5个阶段研究:准备阶段,前机与后机处于起始进近定位点(initial approach fix, IAF)和最后进近定位点(final approach fix, FAF)之间,配对飞机具备各自的起始进近速度,在给定的高度飞行直到捕捉其下滑道,后沿下滑道进近。配对进近中规定后机的最后进近速度vtf应大于前机的最后进近速度vlf,故后机将先于前机停止减速。第1阶段,前机率先到达FAF,以起始进近速度vli,加速度al做近似匀减速运动,后机因为延迟,以起始进近速度vti做时间ttu的匀速运动。第2阶段,后机以起始进近速度vti,加速度at做近似匀减速运动。第3阶段,前机在到达稳定进近点(stable approach point, SAP)时,基本停止减速。最后阶段,配对飞机保持其最后进近速度继续进近,直至前机飞越其跑道入口(threshold, THR)。
在起初的配对进近中,配对飞机的进近航迹是平行的。探究在前机尾流影响下的配对进近,可以发现当后机以一定的角度侧向偏置进近时,能够有效地避开前机的尾流[1],如图1所示。
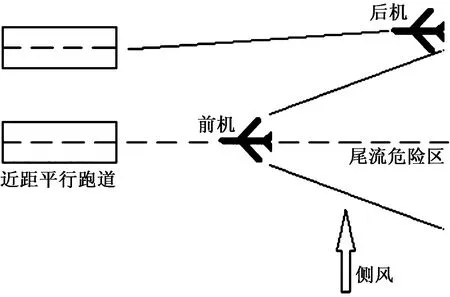
图1 配对进近
2 基于ADS-B的飞机进近纵向定位误差统计分布
在以往的研究中,一般假定定位误差服从常见且易于处理的正态分布。因为不同的定位误差分布会造成存在差异的碰撞风险结果,所以很有必要研究定位误差的真实分布。
收集2020年4—6月在上海虹桥国际机场18L跑道进行着陆的部分航班的ADS-B数据,从中共筛选得到824组飞机最后进近的数据。先对数据做线性插值,得到周期为1 s的飞机定位序列;后将飞机实际位置坐标与标称位置坐标相减,求得飞机最后进近的纵向定位误差,进而研究其分布情况。
利用Kolmogorov-Smirnov单样本分布检验(K-S检验),检验定位误差的样本是否服从正态分布F0(x),假定定位误差的真实分布为F(x),做出问题的假设如下。
H0:F(x)=F0(x),对所有x值⟺,
H1:F(x)≠F0(x),对至少一个x值。
检验统计量为
Dn=supx|S(x)-F0(x)|
(1)
式(1)中:S(x)为该组数据的经验分布。
对于给定的显著性水平χ,临界值为dχ,满足
P(Dn>dχ)=χ
(2)
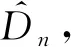
利用SPSS对定位误差做K-S检验,检验结果如表1所示。
定位误差的K-S值为Z=9.685,P<0.05,对于给定的显著性水平χ=0.05,应拒绝零假设,故不可以直接假定定位误差服从正态分布。
鉴于定位误差分布的未知性,利用Python,从其80个分布中筛选出误差平方和较小的3个分布,表2给出拟合效果较好的3个分布的均方差。
从表2可以看出,在所有的分布中,无界约翰逊分布(Johnsonsu)的均方差最小,拟合效果最佳,如图2所示。
综上所述,通过假定飞机纵向定位误差的分布为无界约翰逊分布来评估配对进近纵向碰撞风险。假定无界约翰逊分布的定位参数为μ,尺度参数为σ,形状参数为a、b,其概率密度函数为

表1 K-S检验结果

表2 均方差
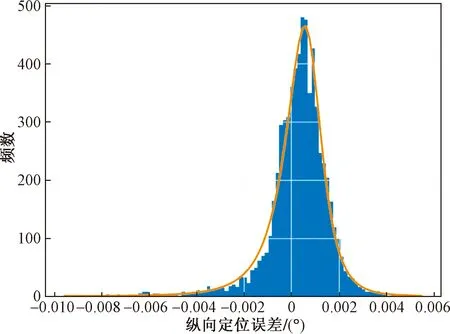
图2 定位误差分布拟合
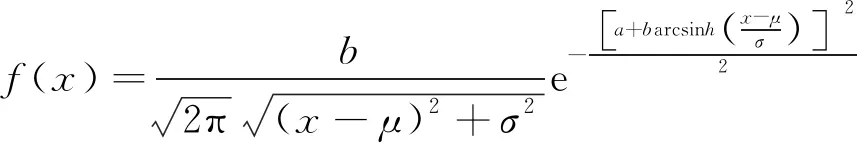
(3)
3 配对进近纵向碰撞风险评估
3.1 建立配对进近纵向碰撞风险评估模型
假定在时刻t,配对飞机实际位置的纵向间隔为S′(t),则S′(t)=S(t)+ε(t),其中,S(t)为在时刻t,配对飞机标称位置的纵向间隔,ε(t)为在时刻t,配对飞机之间的纵向定位误差。经上述分布拟合,假定ε(t)服从无界约翰逊分布。
S′(t)的概率密度函数为
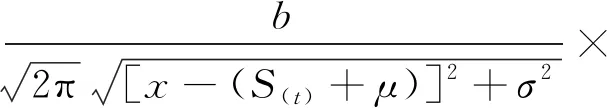

(4)
此时前后两机配对进近纵向碰撞风险评估模型为
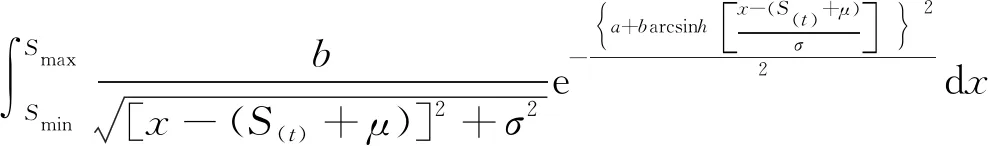
(5)
在考虑下滑角和后机侧向偏置进近的情形下,第1阶段至最后阶段各个阶段的配对飞机标称位置的纵向间隔S(t)的表达式为
第1阶段,当0≤t≤ttu时,
第2阶段,当ttu≤t≤ttu+ttd时,

cosβcosγ。
第3阶段,当ttu+ttd≤t≤tld时,
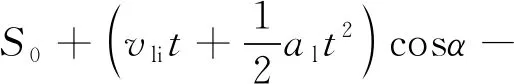
最后阶段,当tld≤t≤tld+tlu时,
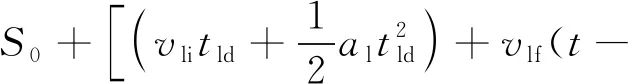
式中:S0为配对飞机的起始纵向间隔;β为后机的下滑角;γ为后机的侧向偏置角。
3.2 确定模型积分区间
配对进近纵向碰撞风险评估模型积分下限主要考虑前机偏航,两机的纵向间隔可以允许后机执行机动避让,从而避免两机相撞;积分下限为两机机身长度和的一半,即
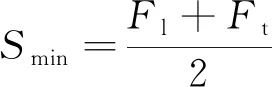
(6)
式(6)中:Fl、Ft分别为前机与后机的机身长度。
积分上限主要考虑后机可以在前机尾流到达其进近航迹之前飞行,从而避开尾流。尾流的起始危险区域宽度[14-15]为
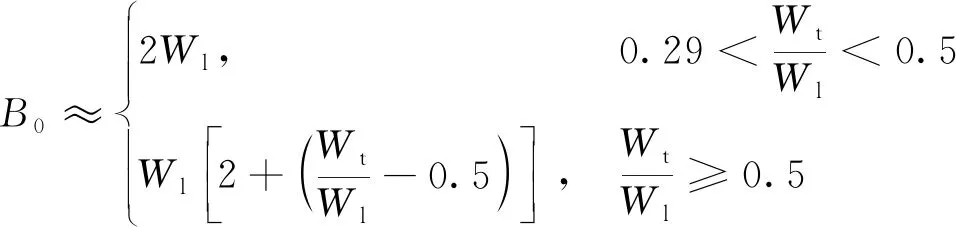
(7)
式中:Wl、Wt分别为前机与后机的翼展。
综合考虑地面效应和不利侧风对尾流的影响,假定前机产生的尾流到达后机进近航迹的时间为
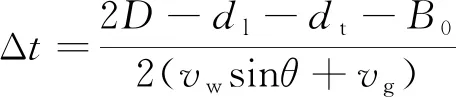
(8)
式(8)中:D为跑道中心线之间的距离;dl、dt分别为平行跑道的宽度;vw为侧风风速;θ为侧风风向,vg为在地面效应作用下尾流的侧移速度。
静风时,尾流相对前机的运动速度为
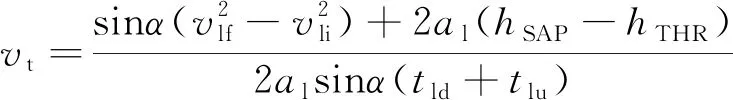
(9)
将上述参数代入计算可得积分上限为
(10)
4 算例仿真
对上海虹桥国际机场的近距平行跑道做配对进近仿真,跑道18L的宽度为45 m,跑道18R的宽度为60 m,跑道中心线的间距为365 m。选取配对进近前机为中型机B737-800,后机为重型机B747-400。通过调研,给定配对进近运行过程和配对飞机的相关参数,如表3、表4所示。
计算各个阶段的近距平行跑道配对飞机的纵向间隔和纵向碰撞风险。仿真结果如表5、图3和图4所示。
由图3可知,随着配对时间的增加,配对飞机的纵向间隔不断减小,在前机飞越其跑道入口时,配对飞机的纵向间隔达到最小。

表4 配对飞机相关参数
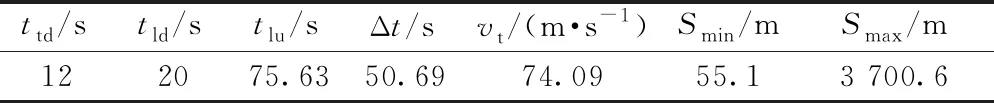
表5 相关参数仿真结果

图3 配对飞机纵向间隔与时间的关系
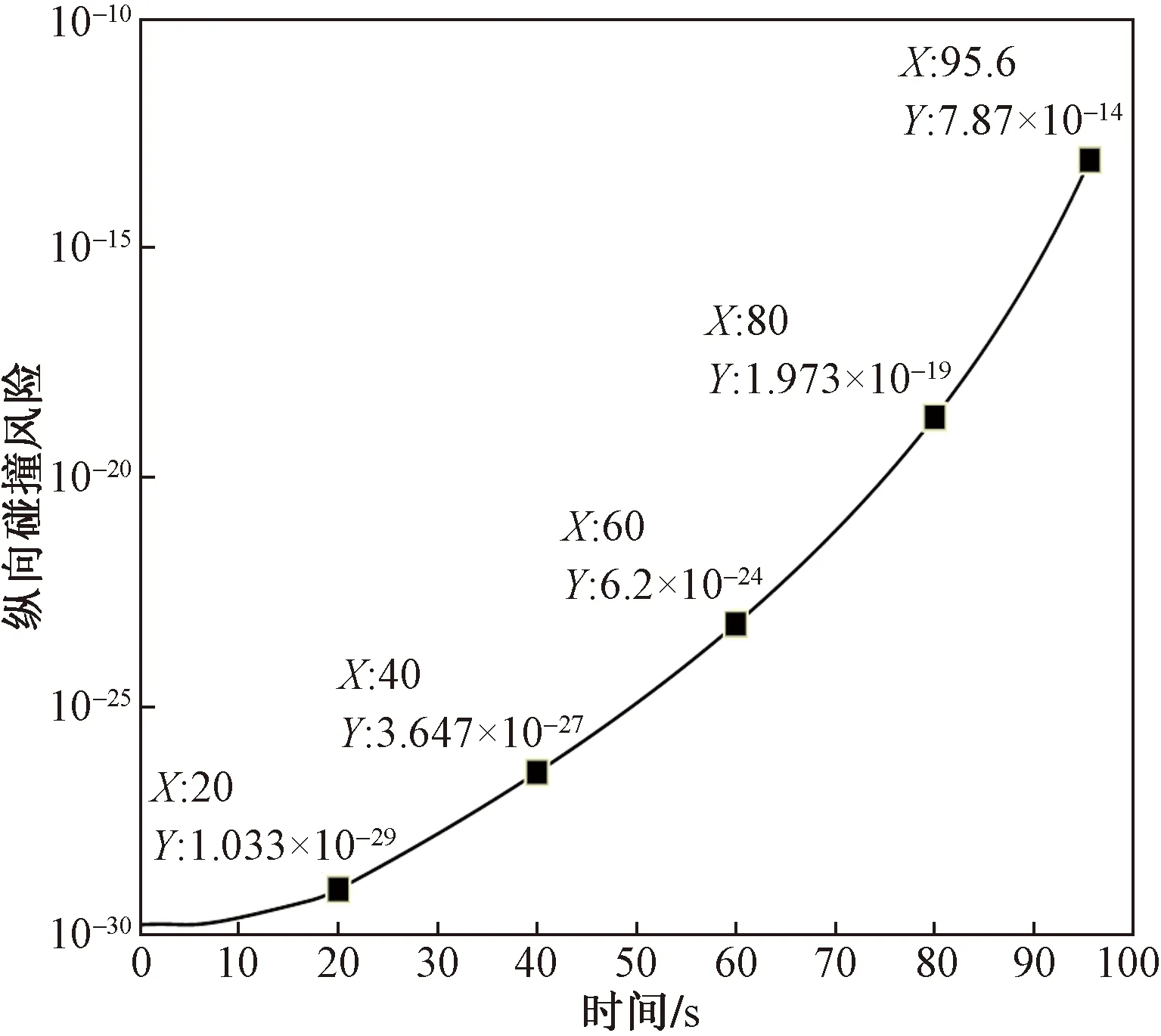
图4 配对飞机纵向碰撞风险与时间的关系
由图4可知,随着配对时间的增加,由于配对飞机的纵向间隔减小,使得配对飞机的纵向碰撞风险不断增大,纵向碰撞风险在前机飞越其跑道入口时达到最大值7.87×10-14。国际民航组织对纵向碰撞风险的规定是1.5×10-9[16],因此在配对进近的整个过程,纵向碰撞风险都在安全目标水平之内,由此可检验模型的有效性。
5 结论
(1)分析了配对飞机在近距平行跑道进近的过程,量化了配对进近各个阶段的时间,并建立了相应的运动学模型;拟合了基于ADS-B的飞机进近纵向定位误差的统计分布,在后机侧向偏置进近的情形下,给出了评估配对进近纵向碰撞风险的模型;借助算例仿真,检验了模型的有效性。
(2)由于机场跑道入口存在内移现象,后续可以考虑错列情形下的配对进近纵向碰撞风险,并对给定的相关参数做灵敏度分析,讨论参数的变化如何影响纵向碰撞风险。
(3)可以将本文研究思路进一步应用于侧向和垂直方向上的配对进近碰撞风险评估。
