车辆非线性悬架系统时滞瞬时最优控制

闫 盖， 方明霞

(1.上海第二工业大学工学部， 上海 201209； 2.同济大学航空航天与力学学院， 上海 200092)

随着科技的发展，车辆悬架进入了电子控制时代，主动/半主动悬架得到越来越多的应用，而由于信号采集传输、控制运算及作动延迟，时滞在控制回路中不可避免。已有研究表明即使很小的时滞也可能导致系统控制效率降低，甚至导致系统失稳。因此，近年来考虑时滞的汽车主动/半主动悬架系统成为学者的研究热点，取得了一些研究成果。文献[1]以含时滞的1/4车辆悬架为对象，分析了时滞天棚开关控制半主动悬架控制系统的时滞渐进稳定性机理；文献[2]提出采用基于自适应模糊逻辑的滑模控制策略，针对磁流变悬架系统执行器件非线性和时滞的不确定性具有良好的控制效果；文献[3]利用平均法对含时滞的半主动汽车悬架进行了解析研究，得到了时滞和稳定性的关系；文献[4]采用多项式判别定理和全时滞稳定性定理绘制了悬架阻尼与控制增益参数平面内的全时滞稳定性区域图，并通过遗传算法优化了参数，获得了更好的减振效果；文献[5]通过多项式判别定理和常微分理论分析了车辆悬架系统的时滞稳定性，并通过状态变换设计时滞反馈最优控制律，保证了系统的稳定性，改善了减振性能；文献[6]采用随机预瞄控制策略对存在控制时滞的车辆主动悬架进行研究，并指出了如果不考虑时滞的影响，悬架系统可能发生不稳定现象；文献[7]采用理论与实验相结合，通过H∞控制理论设计了在一定时滞量下的H∞控制律，并分析了系统的时滞稳定性，最后仿真和实验结果说明了理论推导的正确性和有效性。

虽然目前研究给出了一些卓有成效的时滞消除、补偿和利用方法，但多数将悬架系统简化为线性振动控制系统，而主动/半主动车辆悬架系统结构复杂，且悬架与车架之间的连接多使用橡胶衬套元件，致使悬架系统具有较强的结构非线性。因此，综合考虑悬架系统非线性、控制回路时滞的影响，研究系统的减振特性，是当前研究的热点和难点。现通过理论与仿真方法对含时滞车辆非线性悬架系统动力学特性进行研究，分析非线性参数和控制回路时滞对系统性能的影响，采用最优控制理论和龙格库塔法设计时滞瞬时最优控制律，最后通过仿真验证设计的有效性。

1 含时滞车辆非线性悬架系统动力学模型

因为橡胶衬套具有迟滞非线性特性，目前应用较为广泛的迟滞非线性模型有双线性滞后非线性模型、Bouc-Wen模型、多项式模型、Davidenkov模型和非对称滞后非线性模型等。采用立方非线性多项式模型，即利用系统位移和速度的多项式函数拟合迟滞非线性力。另外，车身的垂直振动是影响车辆平顺性的主要因素，而且车辆的结构复杂，现忽略车身的俯仰和侧倾运动，采用磁流变阻尼器作为执行器，建立了1/4车辆二自由度含时滞非线性悬架模型，如图1所示。

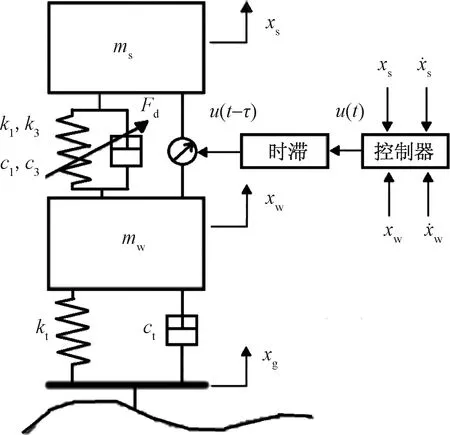
ms为簧载质量，kg；mw为非簧载质量，kg；Fd为悬架系统非线性力，N；k1、k3分别为非线性悬架的线性刚度和非线性刚度，N/m；c1、c3分别为非线性悬架的线性阻尼和非线性阻尼，N·s/m；kt、ct分别为轮胎刚度(N/m)和阻尼(N·s/m)；xs、xw分别为簧载质量位移和非簧载质量位移，m； u(t)为控制器计算输出的控制力，N；τ为悬架控制系统控制回路中的时滞，s；u(t-τ)为系统实际控制力，N；xg为路面不平度，m

利用牛顿运动定律，得到非线性悬架系统的动力学方程为

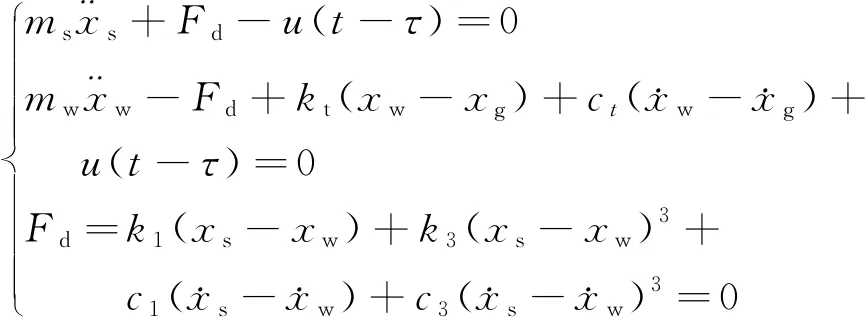
(1)

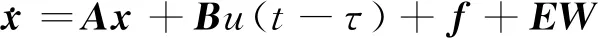
(2)

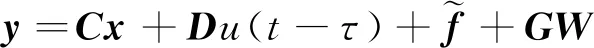
(3)

2 非线性悬架系统时滞瞬时最优控制律设计

采用状态变换方法[8-10]对含时滞的非线性悬架系统时滞瞬时最优控制律进行设计，以保证系统的稳定性。且文献[5]中通过状态变换法设计了时滞反馈控制律，通过理论和实验研究了线性车辆悬架系统主动控制，基于此，将该方法推广应用到非线性悬架系统。针对含时滞的状态方程(2)，进行如下状态变换，即

(4)

则

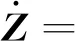
Bu(τ+η)+Be-Aτu(t)

(5)

根据式(3)～式(5)可将状态方程转换为不显含时滞的非线性状态方程，即

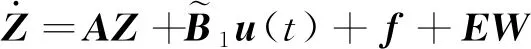
(6)

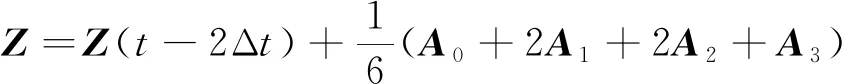
(7)

式(7)中：Δt为数值计算的步长；A0、A1、A2、A3为t-2Δt、t-Δt和t的函数。

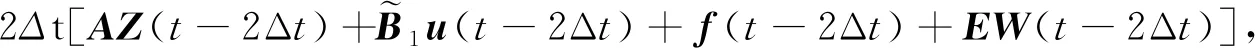
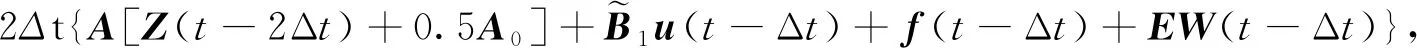
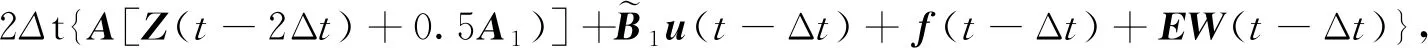
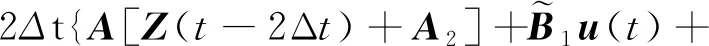
f(t)+EW(t)}。

为了简化式子，令

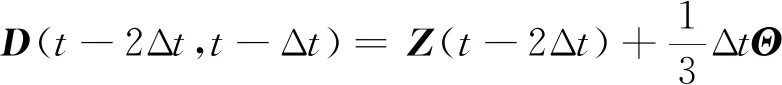
(8)

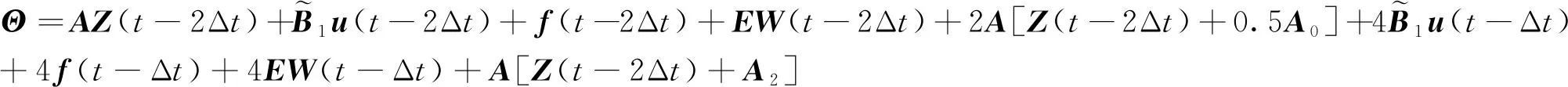
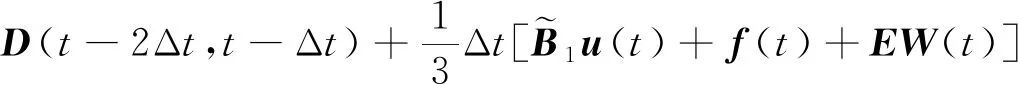
(9)

取时滞反馈最优控制器性能指标为

J(t)=ZT(t)QZ(t)+uT(t)Ru(t)

(10)

式(10)中：Q为非负定对称矩阵；R为正定增益矩阵。非线性系统时滞反馈最优控制是在式(9)的约束下使得系统性能指标J(t)取得最小值。现定义Hamilton函数为

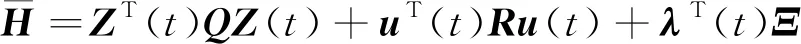
(11)

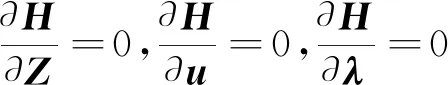
(12)

将式(11)代入式(12)，可以获得非线性系统时滞反馈最优控制律：

(13)

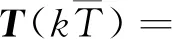
(14)

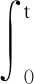
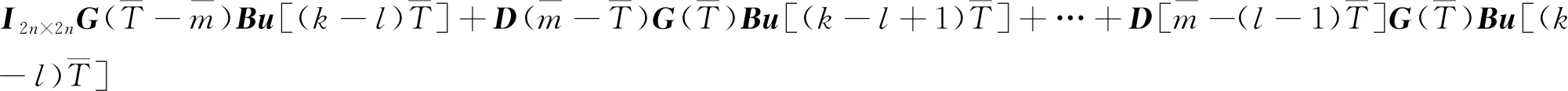
(15)

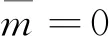
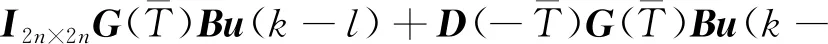
(16)

式中：G(t)可通过式(17)进行迭代计算：

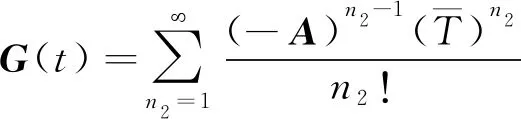
(17)

当t给定时，G(t)将于有限步趋于常数矩阵[11]。

3 车辆非线性悬架系统时滞瞬时最优控制仿真分析

3.1 确定性激励下系统控制特性

以某汽车悬架系统参数为参考，仿真分析中取悬架系统参数为ms=843 kg，mw=98 kg，k1=45 482 N/m，c1=2 546.5 N·s/m，k3=111 324 N/m，c3=4 102 N·s/m，kt=604 685 N/m，ct=370 N·s/m，路面不平度取正弦激励xg=A0sin(2πft)，激励幅值分别取A0=0.004 m，激励频率取f=5 Hz，并令Q=diag([1×108,1×108,1×108,1×108])，R=1。由于时滞在控制中不可避免，在文献[4]也证明了即使很小的时滞也会导致系统失稳发散，因此为了证明非线性悬架时滞瞬时最优控制的有效性，现分析不同时滞下系统的响应特性，图2所示为部分不同固有时滞下非线性悬架系统时滞瞬时最优控制簧载质量加速度。

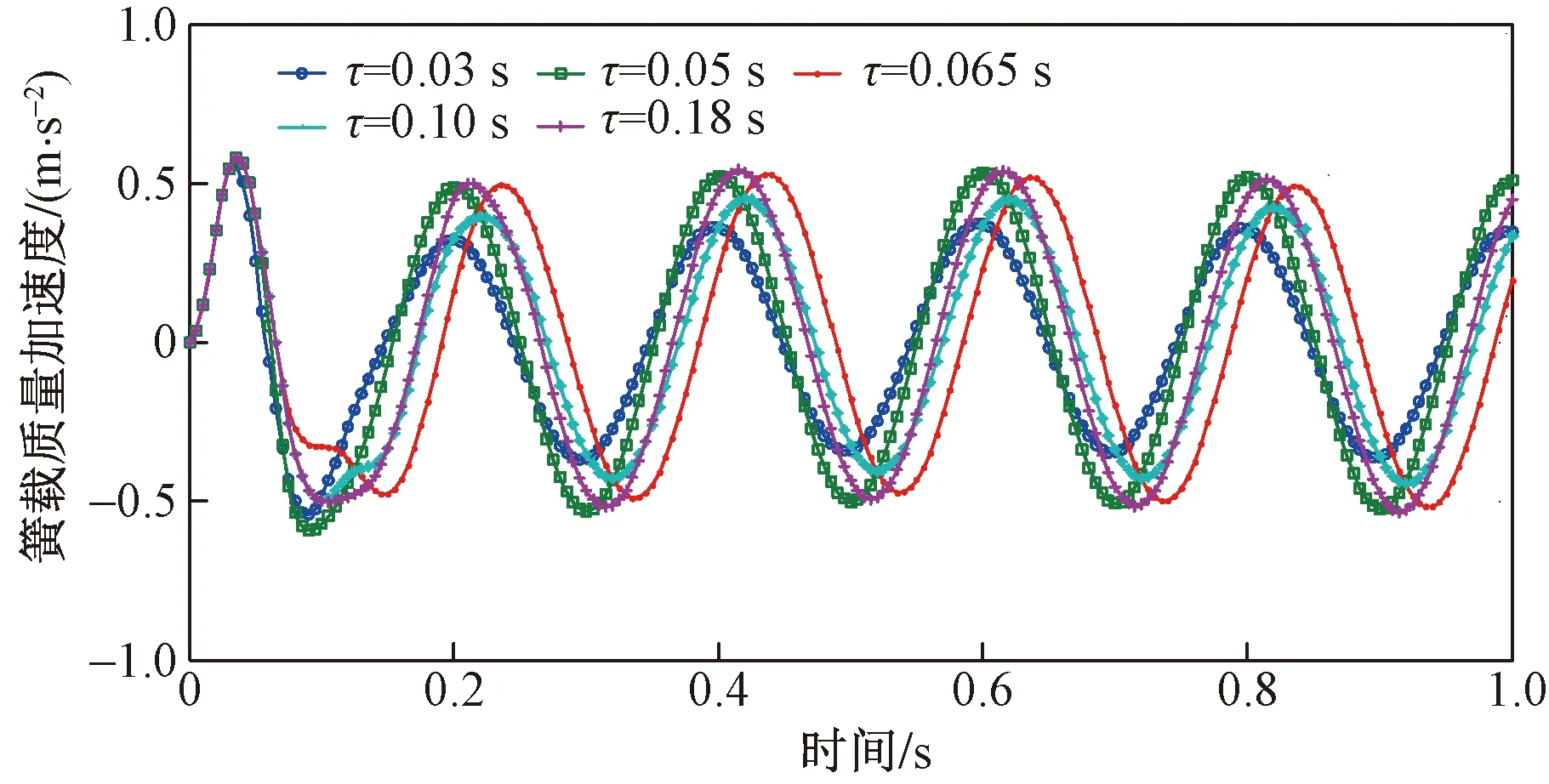
图2 确定性激励下非线性悬架系统时滞瞬时最优控制簧载质量加速度

从图2可以看出，非线性悬架系统在非线性时滞瞬时最优控制下保持稳定，当时滞为0.03 s时，簧载质量加速度幅值为0.36 m/s2；当时滞为 0.065 s 时，簧载质量加速度幅值为0.50 m/s2；当控制回路时滞继续增大时，发现簧载质量加速度值变化不大，且悬架动行程和轮胎动载荷均在允许范围内，保证了悬架的减振性能。响应幅值还受到控制加权矩阵影响，通过调节控制加权矩阵可获得更好的减振效果，如Q=diag[5×108,1×104,5×108,1×106]、R=0.01时，在控制回路时滞为0.065 s时，系统簧载质量加速度如图3所示。

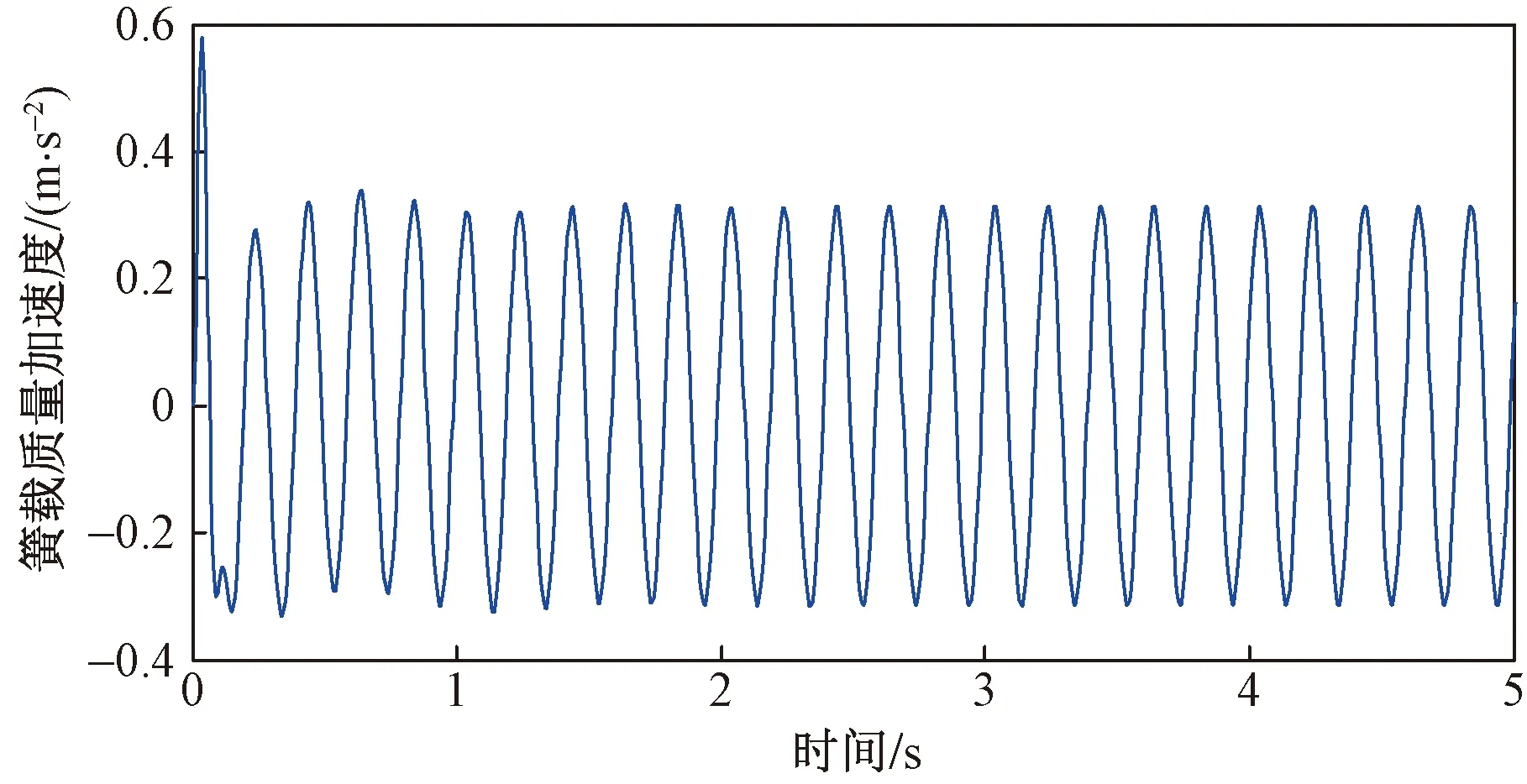
图3 非线性悬架时滞瞬时最优控制簧载质量加速度

从图3可以看出，调整控制加权系数后，在控制时滞为0.065 s时，悬架系统簧载质量加速度幅值从0.50 m/s2降为0.31 m/s2，降幅达38%；悬架动行程和轮胎动载荷均在允许范围内，悬架系统的舒适性被大幅提高。因此在具体实践中，可先测量系统控制回路中时滞量，通过优化算法获取最优的控制加权系数矩阵，进而保证悬架系统实现最好的减振性能。

3.2 随机激励下系统控制特性

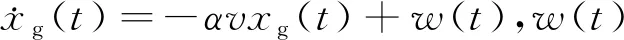
从图4可以看出，随时滞的变化，簧载质量加速度也有所变化，将系统输出响应幅值的均方根(RMS)值填入表1中。

由表1可以发现，随着时滞的变化，簧载质量加速度幅值均方根值随之变化，与确定性激励下响应变化趋势一致，系统均保持稳定，同样可以通过改变控制加权矩阵进一步提高悬架性能。另外，从图2和表1中还可以发现：随着控制回路时滞的增大，确定性激励下系统响应幅值和随机激励下系统的响应均方根值有的变小，有的变大，即控制效果可能变好，也可能变差，这为如何在系统固有控制回路时滞基础上，人为引入控制主动时滞[13]，获得更好的减振性能提供了理论依据，为工程应用奠定了基础。

图4 随机激励下非线性悬架系统时滞瞬时最优控制簧载质量加速度

4 结论

以1/4车辆二自由度含时滞非线性悬架系统为研究对象，采用理论与仿真相结合的方法，研究了非线性悬架系统时滞瞬时最优控制特性，获得以下主要结论。

(1)用立方多项式模型描述悬架非线性力，建立了含时滞车辆非线性悬架动力学模型。通过状态变换思想，将含有时滞的系统状态方程转换成不显含时滞的状态方程。

(2)采用最优控制理论与龙格库塔法设计了车辆非线性悬架时滞瞬时最优控制律，并通过数值仿真分析了确定性激励和随即激励下系统的输出响应。结果表明，时滞瞬时最优控制律可以保证系统的稳定性，优化控制权重矩阵可以获得更好的减振效果。

(3)随着控制回路时滞的变化，系统减振效果可能变好也可能变差，为将时滞作为可调参数，在系统固有时滞基础上，人为引入控制主动时滞获得更优的减振性能提供了理论依据，为主动控制提供了新的思路。