基于修正加速度的对数归一化变步长自适应滤波的心率估计算法

谭 拥， 余成波, 张 林

(重庆理工大学电气与电子工程学院， 重庆 401320)

光电容积脉搏波(photoplethysmography，PPG)描记图法的原理是利用心脏泵血导致外周动脉发生血液容积变化，通过特定波长的光去检测这种变化，将这种变化以反射光强的方式记录下来。与心电图(electrocardiogram，ECG)不同，PPG测量设备不需要紧贴皮肤，减少了佩戴者的不适感，但这也使得PPG信号易受到因人体运动而产生的运动伪影(motion artifact，MA)的影响，致使PPG信号质量变差，提取相关信息困难，这也是目前测量PPG信号面临最大的挑战。

针对上述问题，研究者们提出许多去运动伪影方法。传统的频域分析法，如快速傅里叶变换[1]，通过能量分析来滤除运动噪声，继而获得心率。但该方法只适用于静止或噪声较小的情况。Zhang等[2]提出了TRIOKA框架，该方法利用带通滤波、奇异值分解，对奇异值聚类分组，以加速度作为参考信号去除相关噪声，从而使信号稀疏化，最后利用稀疏信号重构(sparse signal reconstruction，SSR)获得一个高分辨率的PPG信号，对一般运动下的PPG信号能够获得较为准确的心率，然而该方法复杂度较高，易造成冗余,资源浪费，不适用于长时间监测。孙斌等[3]学者统计静止状态下PPG信号的峰度、偏度等指标，以此判断PPG信号是否被污染，并将污染的PPG信号片段剪切，以达到去除运动伪影的目的，虽然降低了复杂度，但去除运动伪影的同时也把有用信息剪切掉。Dragomiretskiy等[4]学者在经验模态分解的基础上提出一个完全非递归的变分模态分解(variational mode decom-position，VMD)模型，有效的解决了模态混叠的问题。Sharma[5]使用VMD对PPG信号进行分解、重构，但只对静止状态下的PPG信号进行了研究。此外，还有其他抗运动伪影方法，如集合经验模态分解、自适应滤波法[6-7]等，均未在复杂度和准确率之间寻找到折中点。

运动伪影主要由外部运动所造成的，因此研究者将加速度[2,6-7]作为去除MA的参考信号。然而加速度计是基于惯性参考系[8-9]测量，得到的加速度信号会受到重力分量的影响。Jarchi等[10]在采集多种运动下PPG信号时，还采集了加速度以及三轴角速度。利用陀螺仪测出的三轴角速度将加速度映射到传感器参考系[8]，从而修正加速度，获得更准确地心率估计值。

结合加速度和运动伪影的特点，提出一种基于修正加速度的对数归一化变步长自适应滤波算法。该算法对PPG信号进行0.4～5 Hz的带通滤波，用三轴角速度对三轴加速度进行卡尔曼滤波修正，然后将修正后的加速度作为Log-NLMS自适应滤波器的参考信号，滤除运动伪影，从而得到高质量的PPG信号，最后，通过频域的谱峰准追踪来估计心率值。此外，从同步采集的ECG信号中获取真实心率，来验证本文算法的抗运动干扰能力与心率估计的准确性。

1 心率估计算法

所提出的基于修正的加速度的运动伪影去除算法主要包含：数据预处理、加速度的修正、PPG信号的自适应滤波和谱峰追踪，其流程图如图1所示。

1.1 数据预处理

根据人体正常心率范围，首先对原PPG信号进行0.4～5 Hz的带通滤波[2,11]。去除该范围以外的运动噪声、工频干扰以及基线漂移，不仅达到使信号稀疏化的目的，而且还消除了多余的噪声干扰，为接下来的信号自适应滤波创造更有利的去噪条件。

1.2 加速度修正

在运动状态下，加速度计测量的惯性参考系下加速度信号是由重力加速度和外部加速度的共同作用的结果，如式(1)所示，这样会导致外部加速度测量误差较大。

YA=Sg+Sa+nA

(1)

式(1)中：上标S表示惯性参考系；下标A表示加速度计；YA、nA分别表示加速度计测量值和测量误差；Sg为重力分量；Sa为外部加速度分量。

根据文献[8]基于旋转的过程，将惯性参考系下的重力映射到传感器参考系下，消除重力分量影响，修正加速度，可分别表示为

Sg=g×SZ

(2)

SZ=[-sinβcosβsinγcosβcosγ]

(3)

式中：β、γ分别为俯仰角和翻滚角，可由陀螺仪获得；g为重力加速度，9.8 m/s2；SZ为旋转向量。

利用六轴加速度传感器获得的加速度和角速度。然而，陀螺仪测量的角速度需要通过积分才能获得俯仰角和翻滚角，由测量误差积分所产生的误差是令人无法接受的，因此陀螺仪不能用于长时间的角度测量，需要隔一段时间对陀螺仪测量姿态角进行修正。这种误差可以通过卡尔曼滤波的方法来减小[10,12]，从而有效将传感器参考系下的加速度中的重力分量去除。采用线性卡尔曼滤波，其定义为

Xk=AXk-1+wk

(4)

zk=HXk-1+vk

(5)

式中：A为状态转移矩阵；H为测量矩阵；Xk为k时刻的状态向量；zk为测量值；wk为均值为0、协方差矩阵为Q、且服从正态分布的过程噪声；vk为均值为0，协方差矩阵为R，且服从正态分布的测量噪声。利用捷联式积分，式(1)、式(2)可将状态转移方程和测量方程描述为

SZt=[I-dt(YG,t-1×)]SZt-1-dt(SZt-1×)nG

(6)

(7)

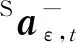
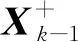
(8)

(9)

计算卡尔曼增益Kk可表示为

(10)

应用卡尔曼增益对当前估计值进行修正：

(11)

(12)

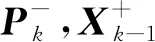
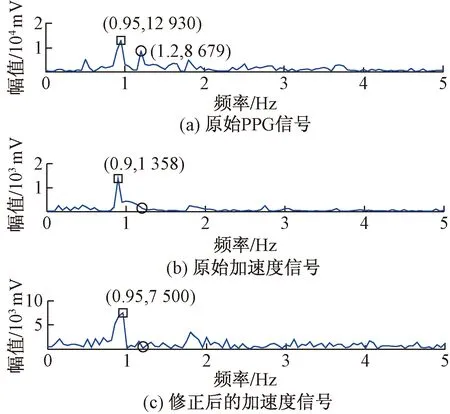
图2 原始PPG信号、原始加速度及修正加速度FFT频对比

1.3 Log-NLMS变步长自适应滤波

归一化最小均方差算法(normalized least mean square，NLMS)是一种改进的自适应滤波算法，它有效解决了最小均方差(least mean square，LMS)算法在收敛速度和误差稳态相互矛盾的问题[6]。该算法用步长和输入信号的功率之比来对原有的固定步长进行归一化处理，在迭代计算中调整步长以及抽头系数，使均方误差快速达到最小，这样既保证了收敛速度，又使得收敛误差稳定在可接受范围内。NLMS算法的步长更新公式为

(13)

(14)

式(14)中：c为一个极小的常数，其作用是避免步长分母为零；W(n)为n时刻的抽头系数；e(n)为n时刻期望信号与输入信号之间误差。

对数函数的最小均方算法(log-least mean square，Log-LMS)是以减小稳态误差，提高收敛速为前提，对传统的sigmoid函数[13]、反正切函数[14]的变步长LMS进行改进的算法。该算法将步长和误差设置为对数关系，有效地解决了收敛速度和误差稳态之间的矛盾[15]。其步长更新表达式为

μ(n)′=blg[a|e(n)|m]

(15)

式(15)中：a表示控制曲线的整体形状走向；m表示控制曲线底部变化速度；b表示控制曲线的幅度大小。

NLMS和Log-LMS虽然在一定程度改善了传统LMS算法的缺点，但NLMS使用了全局步长因子，在一定意义上仍会存在传统LMS算法同样的问题，而Log-LMS算法对输入信号比较敏感[16]。将两种方法的优点进行融合，其步长表达式为

(16)

将修正的加速度信号作为自适应滤波输入， 设置参数滤波器阶数L=3，m=2，a=1 000，b=0.001。如图3所示，Log-NLMS分别将修正前后的加速度作为参考信号所得到的滤波后PPG频谱进行对比。图3(a)为原始PPG信号的频谱图，清楚显示了心率和MA两个主峰，图3(b)为原始加速度信号作为参考信号的Log-NLMS滤波。由于原始加速度主频与图3(a)中的MA主频有所偏差，无法去除与加速度有关的MA，以至于接下来的谱峰追踪无法定位真实心率位置。如图3(c)所示，修正后的加速度作为参考信号，MA主频与图3(a)的MA主频重合，能够较为有效地消除MA，得到准确地心率估计值。

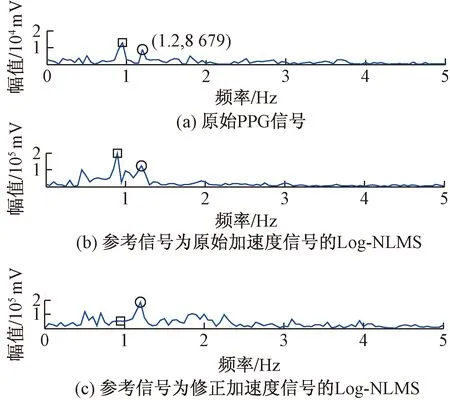
图3 PPG经两种算法滤波后的FFT频对比

1.4 谱峰追踪

经过滤波处理后的PPG信号在时域上的波形如图4(c)所示，虽然在前半段波峰不太突出，但整体上还是能和ECG波峰一一对应，而且接下来的谱峰追踪是从频域上对图3(c)进行心率估计，就更加保证心率估计的正确性。

在心率估计算法中，谱峰追踪是算法中一个重要组成部分。其要求主要包含两点：①Q1：人类的心率短时间内不会发生突变；②Q2：PPG频谱中存在与心率对应的谐波峰，尤其是二次谐波，与基波形成峰值对。谱峰追踪具体如下。

(1)初始化：在该阶段，首先要求测试者保持静止不动，以获得静止时的心率来作为下一个时间窗口心率估计的先验信息。

(2)峰值选择：用Nprev表示上个时间窗口心率在频谱中波峰所对应的索引值。根据Q1可得，存在一个Δs使得当前时间窗口的心率索引在R0=[Nprev-Δs,Nprev-Δs+1,…,Nprev+Δs]这个范围内，而对应的二次谐波则在R1=[2(Nprev-Δs-1)+1,2(Nprev-Δs)+1,…, 2(Nprev+Δs-1)+1]内，在(R0,R1)搜索峰值对。注意，在对应区域中只寻找该区域内大于该区域内最大峰值的30%的峰[2]。

(3)验证：为了防止错误追踪，导致心率估计错误，因此验证结果可靠性是有必要的。根据Q1，规定相邻时间窗口心率不允许相差10 BPM(BPM为每秒钟心脏搏动次数)。因此需要对心率进行验证，其表达式为

(17)

式(17)中：N-表示当前时间窗口选择的峰值索引；Ncur表示验证后的峰值索引；α=6是根据频谱划分网格数N=5 120和采样频率Fs=256 Hz所决定。参数a根据具体情况设置，设a=2。

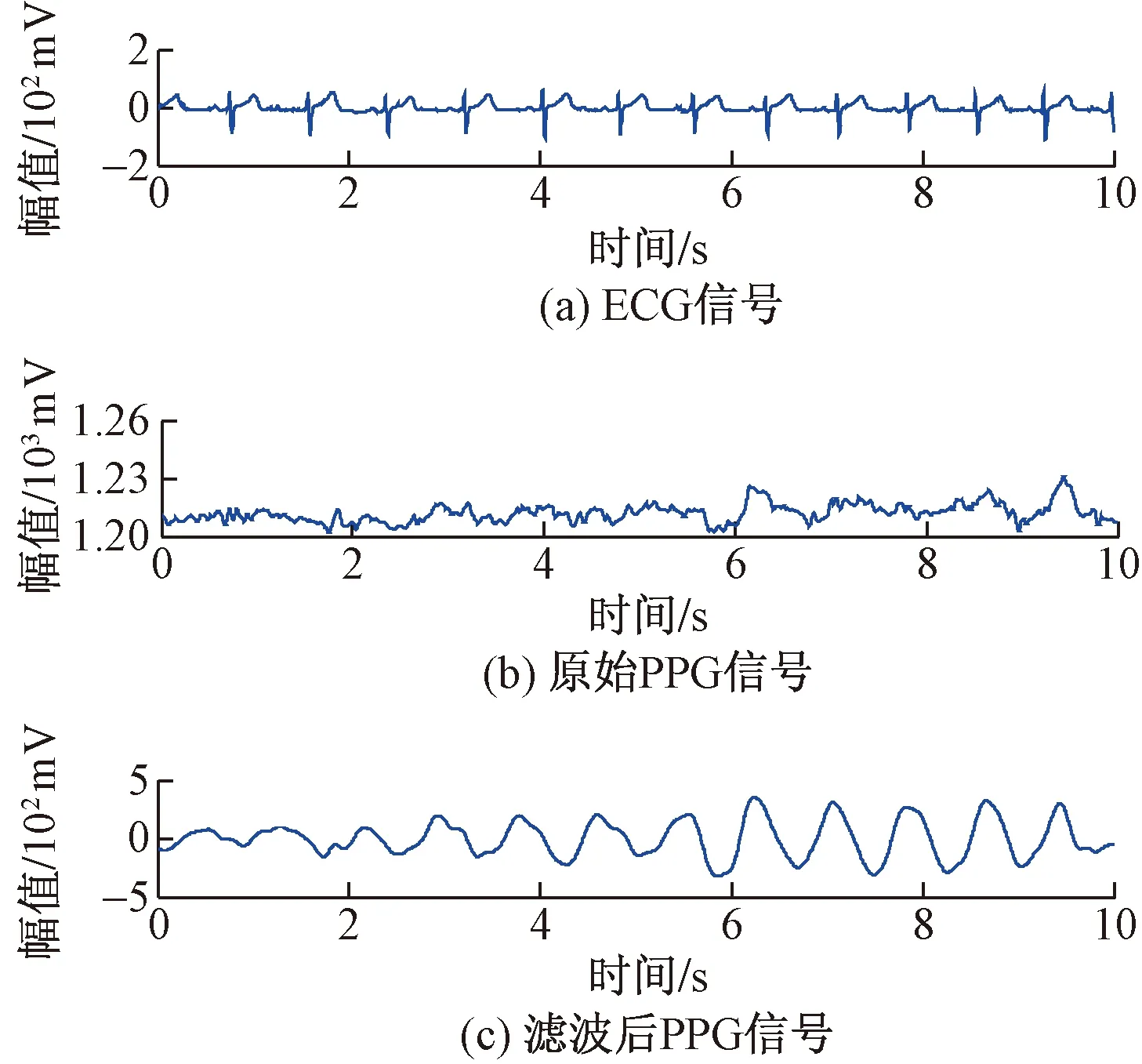
图4 ECG信号与自适应滤波后的PPG信号的对比

2 结果与讨论

2.1 实验数据

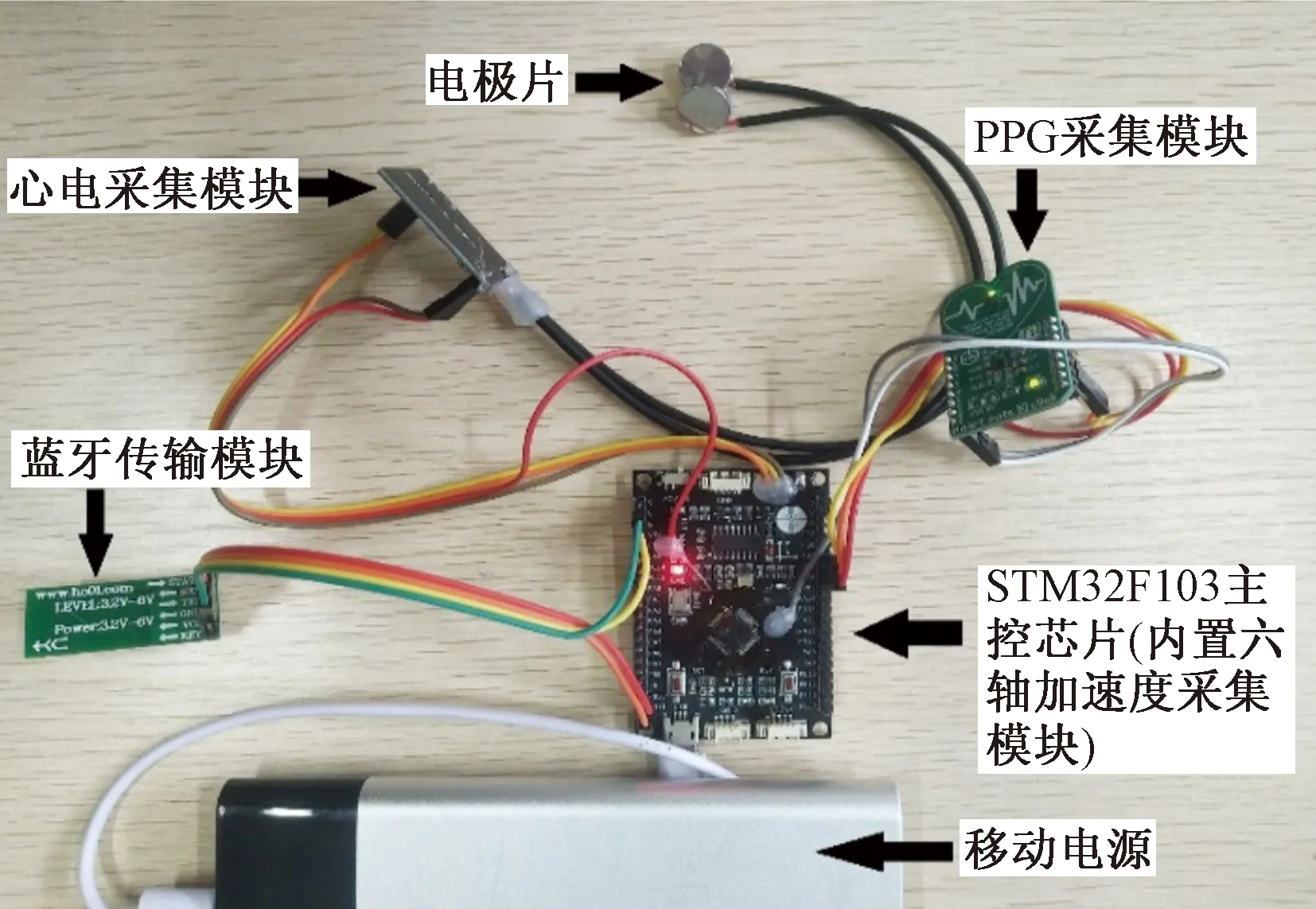
图5 PPG采集装置实物图

主要以模块化的方式采集数据。如图5所示，PPG采集装置以STM32F103为主控芯片，控制PPG信号采集、六轴加速度信号采集、心电信号采集以及蓝牙数据发送。模拟手环戴在手腕上，使用波长535 nm的绿光从手腕采集PPG信号，同时，从六轴加速度采集模块和心电采集模块同步获取六轴加速度信号和心电信号。共采集了常见3种状态：步行、低速骑行、高速骑行。每一种状态都是先保持30 s静止，接下的3 min实施相应的动作，最后保持30 s静止，每实施一种动作需要间隔10 min。实验分别对年龄在20～50岁的3名和2名女性测试者进行了数据采集，每名测试者采集3组数据，分别对应3种不同运动状态。

2.2 评价指标

实验采用平均绝对误差(average absolute error，AAE)和平均相对误差(average relative error，ARE)作为估计心率与真实心率的评价指标，同时还采用Bland-Altman[17]图来验证两者之间的一致性。平均绝对误差定义为

(18)

式(18)中：M表示总的时间窗口个数；HRECG(i)、HRPPG(i)分别表示第i个窗口的真实心率和估计心率。平均相对误差定义为

(19)

Bland-Altman图用来检验估计值与真实值之间的一致性，其横坐标为两者的均值，纵坐标为两者之间的差值，以此来展示每个估计值和对应的真实值之间的差异。Bland-Altman图划定了一个置信区[Mean-1.96σ, Mean+1.96σ]，其中Mean表示所有估计心率与真实心率差值的均值，σ表示估计心率与真实心率差值的标准差。如果95%及以上数据点的在这个区域内，表示置信度高，一致性好。

2.3 实验结果

PPG采集装置的采样频率统一设置为256 Hz。用一个长为T=10 s的时间窗口以步长S=2 s在每组信号上滑动。采用原始加速度作为参考信号的Log-NLMS(对比算法)和修正加速度作为参考信号的Log-NLMS(本文算法)进行实验，得到的AAE和ARE如表1所示，步行、低速骑行、高速骑行3种状态下，经过本文算法去噪后，测试者的AAE和ARE整体上都比对比算法要低，尤其是高速骑行状态下，本文算法5名测试者的AAE均值2.62 BPM要远低于对比算法AAE均值5.66 BPM。结果表明修正后的加速度作为自适应滤波的参考信号比原始加速度作为自适应滤波的参考信号去噪效果要好，心率估计更加准确。如Bland-Altman图(图6)所示，大部分数据点都在划定的95%置信区内，经计算，本文算法计算的心率与真实心率的误差有93.33%的概率在置信区内，表明本文算法去运动伪影效果以及心率估计都有较高的准确性。

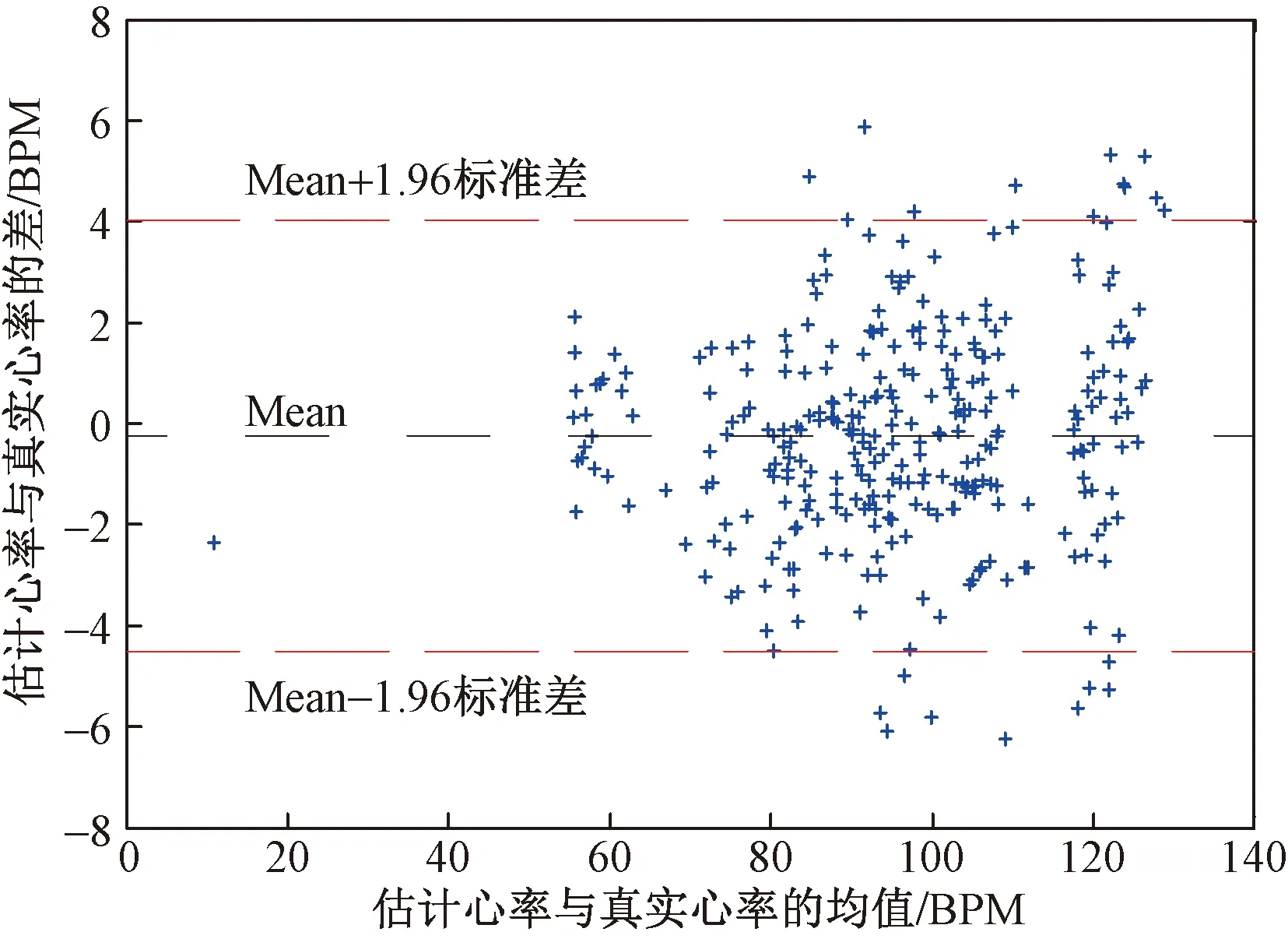
图6 真实心率与本文估计心率的Bland-Altman图

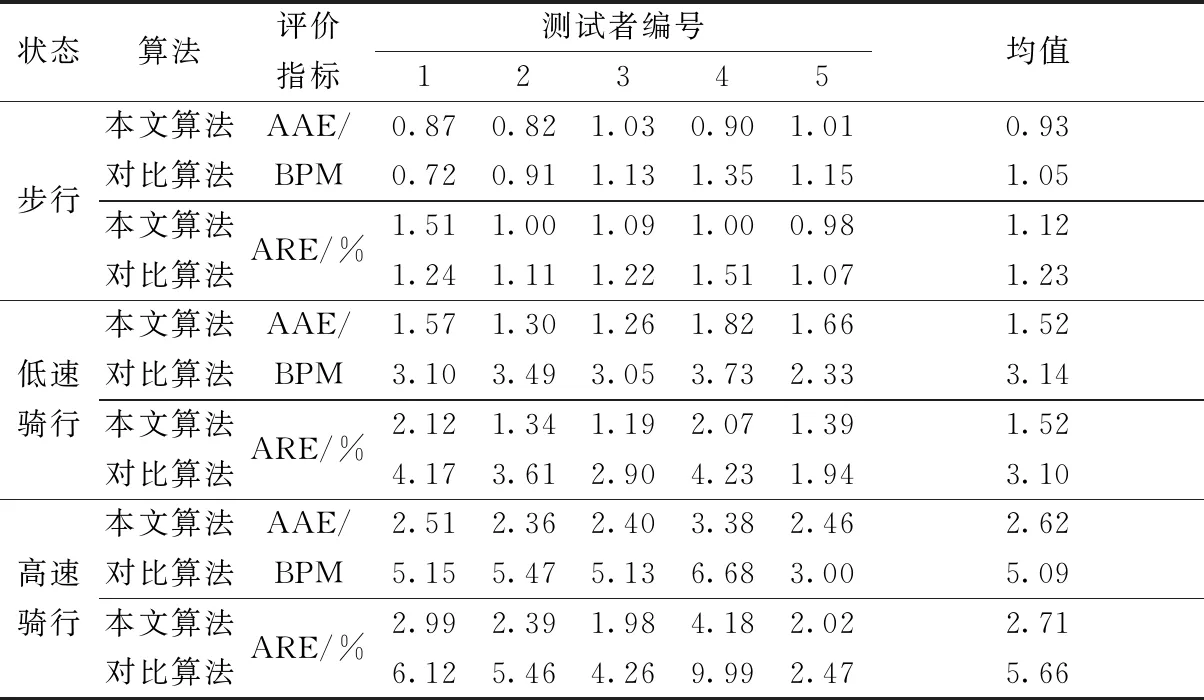
表1 步行、低速骑行和高速骑行状态下两种算法心率提取的AAE、ARE

3 结论

为消除PPG信号中运动伪影的影响，提高心率估计的准确性，设计了一种基于修正加速度变步长自适应滤波的心率估计算法，得到以下结论。

(1)由于加速度计测量是基于惯性参考系，所以测量的加速度包含重力分量，为了得到外部加度，采用卡尔曼滤波对加速度进行修正，消除重力分量的影响，相较于以原始加速度信号为参考信号的心率估计算法，去除MA能力效果更好，心率估计更加准确。

(2)穿戴设备要求的计算准确、功耗低，大部分抗MA算法都未能解决复杂度和精确度两者之间的矛盾。Log-NLMS自适应滤波算法简单，收敛速度块，误差稳态高，符合可穿戴设备的需求。