基于组合信号源的非线性系统的子空间辨识

侯玉雯， 王宏伟,2*

(1.新疆大学电气工程学院， 乌鲁木齐 830047； 2.大连理工大学控制科学与工程学院， 大连 116024)

在非线性系统辨识中，基于块结构非线性动态模型辨识是其中一个研究方向。这类模型同时结合了动态线性模型和静态(无记忆)非线性函数模块，具有较易辨识、计算量少的优点，能较好地反映过程特征，应用非常广泛。这类模型中，Hammerstein模型是经常使用的模型。这种模型能够较好地反映一大类非线性过程，如酸碱度(pH)中和滴定过程、干燥过程、非线性预报器[1]等。近年来，很多学者围绕着Hammerstein模型展开了广泛和深入的研究。

在Hammerstein模型的非线性环节的研究中，Sung等[2]提出一种特殊测试信号对多项式类的非线性进行研究辨识。但对于这种方法，只能针对于多项式，在实际应用中，具有一定局限性。在此基础上，Lü等[3]提出应用神经模糊方法来逼近非线性环节。该方法既可避免迭代，又可以应用于分段非线性函数。而神经网络、模糊系统、神经模糊系统等方法可以任意精度逼近任意非线性系统，所以该法的研究是当前的热点[4-6]。

在Hammerstein模型的参数辨识研究中。主要包括非线性模块的参数辨识和线性模块的参数辨识。这类的辨识方法主要有：迭代法[7]、过参数法[8]、频域法[9]、组合信号源方法。采用组合信号源方式，可以将静态非线性环节和动态线性环节解耦分离，再通过重构中间变量等方法辨识各环节参数。由于利用组合信号将静态非线性环节和动态线性环节隔离开，便于采用不同信号进行分离辨识，这种辨识方法具有简单、计算量小等优点[1,3,10-14]。

在Hammerstein模型中，系统动态模块也可以采用状态空间方程描述，这样更可以准确描述系统外部变量和内部状态变量的变化[15]。文献[16-17]斜交投影的子空间方法对静态非线性模块和动态线性模块的参数进行辨识，但这种方法需要多次采用矩阵奇异值分解方法，计算量较大。另外，基于子空间技术的Hammerstein模型辨识，往往要求静态非线性模块是非线性多项式或者非线性基函数，对于不能用非线性多项式或者非线性基函数描述的复杂非线性系统就不能使用。

针对上述问题，提出基于组合信号源，将模糊神经和子空间辨识算法相融合的辨识方法。本文方法的特点是: ①将伪随机逆M序列编码信号与随机编码信号作为组合信号源，实现非线性模块和线性模块分离；②使用模糊神经网络模型去逼近静态非线性模块，这可以有效避免传统Hammerstein模型的迭代算法，也可以有效避免采用多项式方法逼近非线性函数时的限制，从而拓宽了非线性模型的适用范围；③实现非线性模块和线性模块的状态空间方程模型分离辨识，其中状态空间方程模型采用子空间技术辨识，这样整体计算量小、效率高。

1 模型描述

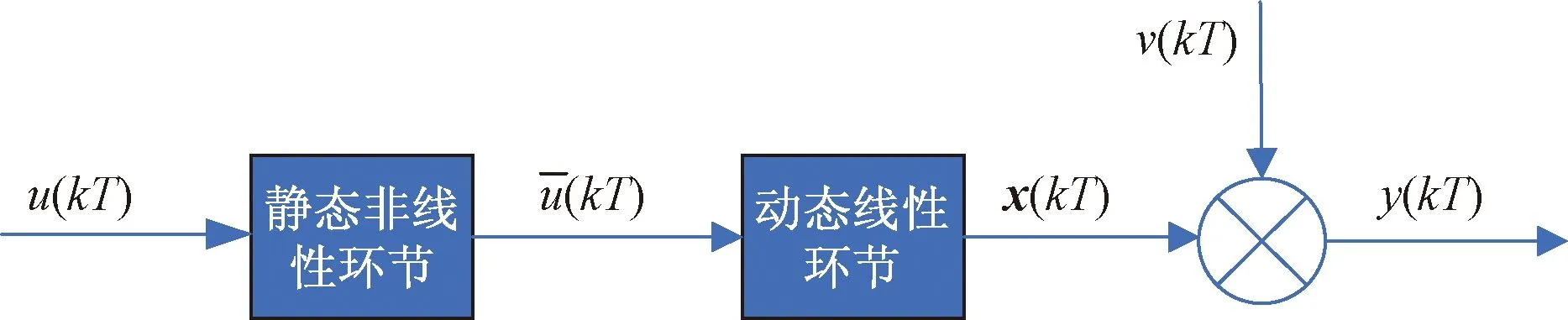
图1 单输入单输出Hammerstein系统结构

图1中，线性环节环节的状态空间方程模型为

(1)

式(1)中：A、B、C为适当维数的矩阵；D为一个常数;u(kT)∈Rr为输入信号；y(kT)∈Rr为系统输出；x(kT)∈Rn为状态向量；v(kT)∈Rr为零均值的随机白噪声，k为当前时刻；T为采样周期。

非线性环节模型为

(2)

实际上，考虑到过程噪声和干扰的影响，式(2)代入式(1)得

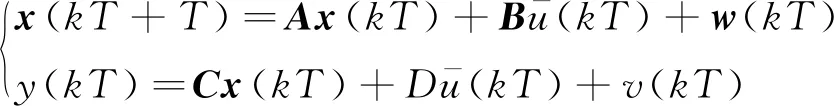
(3)

式(3)中：w(kT)、v(kT)分别为过程噪声和测量噪声，两者均为不可测信号。

采用模糊神经模型拟合静态非线性环节模型，其用Takagi-Sugeno(T-S)模糊模型表示为

(4)

式(4)中：Rl表示第l条规则；u(kT)为输入信号；wl为第l条规则的后件参数；c为规则总数；Fl为模糊集。

模糊神经模型共有四层，具体如下。

(1)第一层为输入层，该层由输入信号u(kT)直接传递给下一层。

(3)第三层为模糊规则层，模糊规则数等于该层的节点数。

(4)第四层为输出层，该层进行反模糊化操作。

模糊神经模型的输出为

(5)

辨识目的是使得如下目标函数最小，即

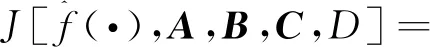
(6)

2 基于组合信号源的模糊神经Hammerstein模型的辨识

2.1 混合激励信号的设计

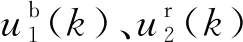
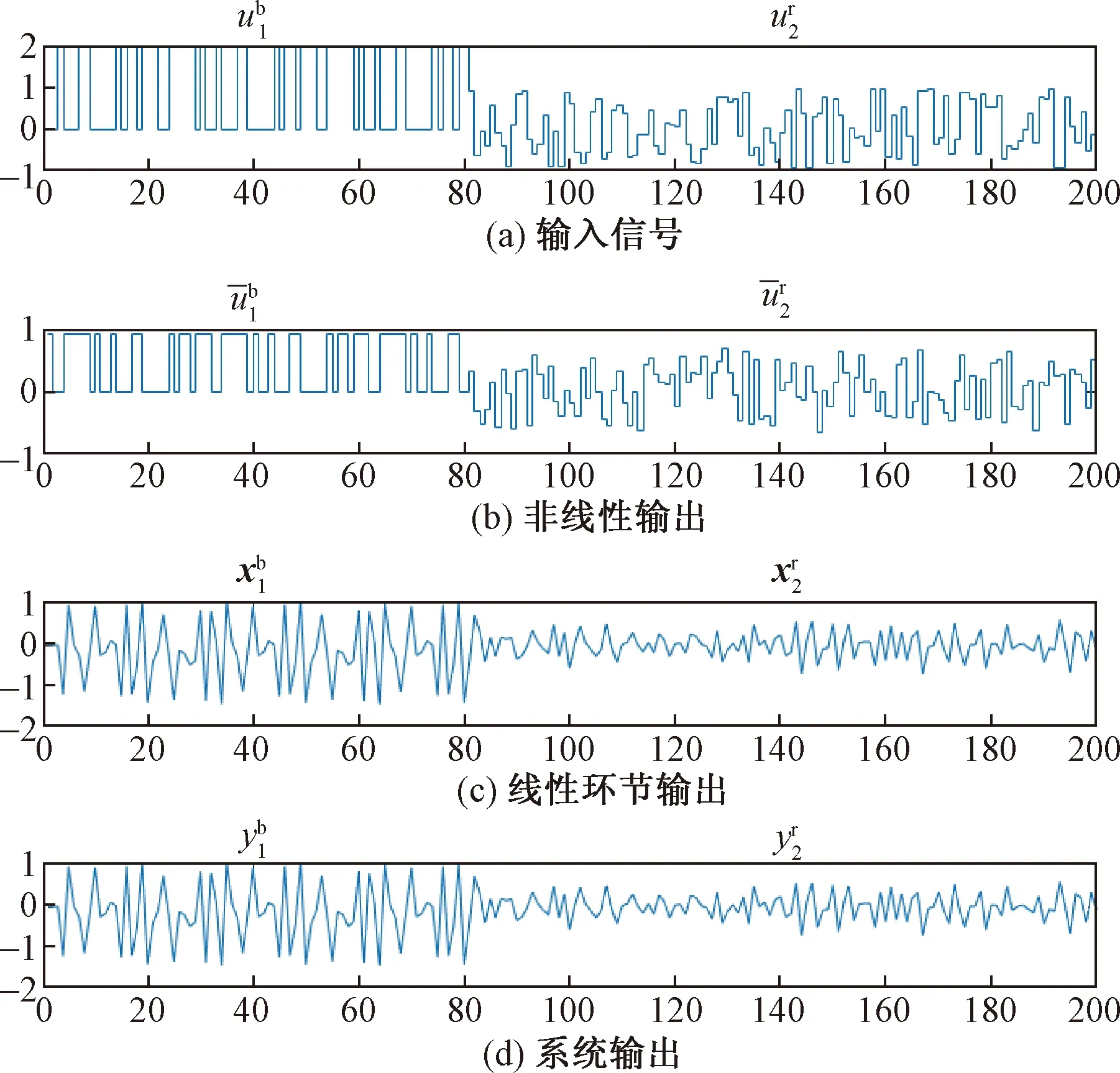
图2 混合信号组成

2.2 动态线性环节模型的子空间辨识

(7)

针对状态空间方程[式(7)]，离散系统的输出方程形式为

(8)

式(8)中：Yf为广义输出矩阵；下标f表示未来的时间标度；Xi为状态序列；Uf为输入的Hankel矩阵；增广观测矩阵Γi可表示为

Γi=[CCACA2…CAi-1]T

(9)

(10)

(11)

重新定义输入输出的Hankel矩阵分别为

(12)

(13)

为了更方便的表达，简记为

(14)

式(14)中：下标p和f分别表示可定义的过去和未来的时刻标度。根据输入输出的Hankel矩阵，同理可得wk和vk的Hankel矩阵，分别记为M0|i-1、Mi|2i-1、N0|i-1、Ni|2i-1，简记为Mp、Mf、Np、Nf。

定义状态序列Xi为

Xi=[xixi+1xi+2…xi+j-1]

(15)

投影的定义如下。

定义一矩阵A的行空间在矩阵B行空间上的正交投影为

A/B=ABT(BBT)+B

(16)

定义二矩阵A的行空间在矩阵B行空间的正交补空间上的正交投影为

A/B⊥=A-ABT(BBT)+B

(17)

式中：上标+表示Moore-Penrose伪逆；B⊥表示B行空间正交补空间，(B⊥)TB=0。

将子空间辨识算法分为两个步骤，具体如下[18]。

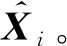
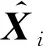
(18)

(19)

选择合适的加权矩阵W1和W2，并在式(19)两端分别左乘W1和右乘W2，可得

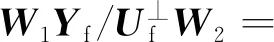
骨折创伤后骨缺损是创伤骨科常遇到的棘手问题。对于较小的缺损（＜5 cm），自体松质骨移植效果良好，但对于较大的缺损（＞5 cm），骨重建过程中易发生骨吸收和骨化不全，导致再骨折。Ilizarov技术、带血管的骨移植是治疗较大骨缺损的经典方法。但Ilizarov技术治疗周期长，操作繁复，患者在治疗期间佩戴外固定架，生活不便。带血管骨移植需要显微缝合血管，手术操作要求高，且移植骨骨化、塑形慢，并存在手术失败的风险。

(20)

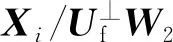
如果均满足上述条件，则定义加权映射矩阵Oi

(21)

将Oi进行奇异值分解(singular value decomposition，SVD)分解,有

(22)

式(22)中：U=[U1，U2]与V[V1，V2]均为正交矩阵，其中U为m维单位正交基，V为n维正交阵，即满足UTU=I和VTV=I。

选择恰当的W2，可得系统状态序列的卡尔曼滤波估计：

(23)

基于子空间的动态线性模型辨识方法总结如下。

Step 1计算Oi和Oi+1,其表达式为

(24)

Step 2对Oi进行SVD分解得

(25)

Step 3根据S1中非零奇异值的个数来确定系统的阶数n。

Step 4计算Γi和Γi-1，则有

(26)

式(26)中：Γi表示由Γi前(i-1)×1行组成的矩阵。

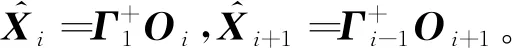
Step 6通过最小二乘估计系统的参数，可得到A、B、C、D。

(27)

式(27)中:ρw和ρv为残差矩阵。

Step 7噪声协方差矩阵Q、S、R由残差值确定。

2.3 静态非线性环节模型的辨识

非线性环节模型为

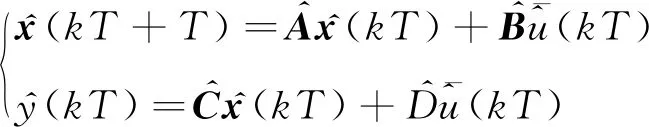
(28)

静态非线性模型辨识方法总结如下。

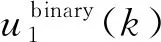
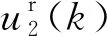
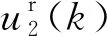
3 仿真算例

3.1 仿真算例1

考虑仿真对象，静态非线性模型选取死区饱和模型为

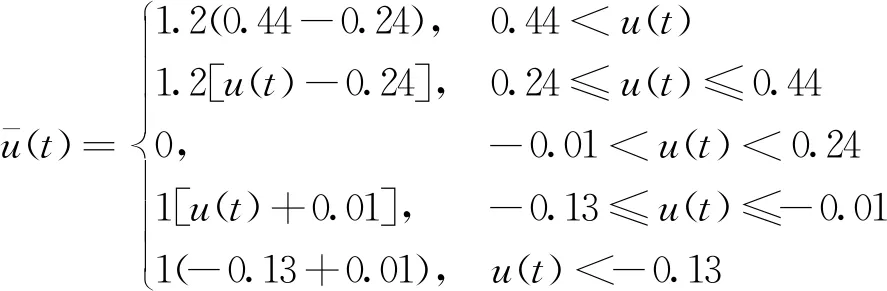
(29)

线性系统选取的离散时间状态空间模型为

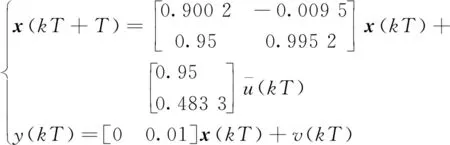
(30)

从图3可以看出，估计模型的奇异值在第一、第二阶时最大，其余都近乎为0。故将模型阶数选为2阶。为了避免实验结果的偶然性，以不同的噪声序列进行100次蒙特-卡罗实验。样本数据长度j=4 000，样本数据行块数i′=10。实验结果如图4、图5所示。

图4分别给出了不同噪信比下的状态空间模型辨识结果。从图4可以看出，当噪声的方差σ2=0.062，信噪比δns=17.8%时，在低频段范围内，辨识模型的bode曲线与原系统的bode曲线基本重合。

图3 估计模型奇异值的变化

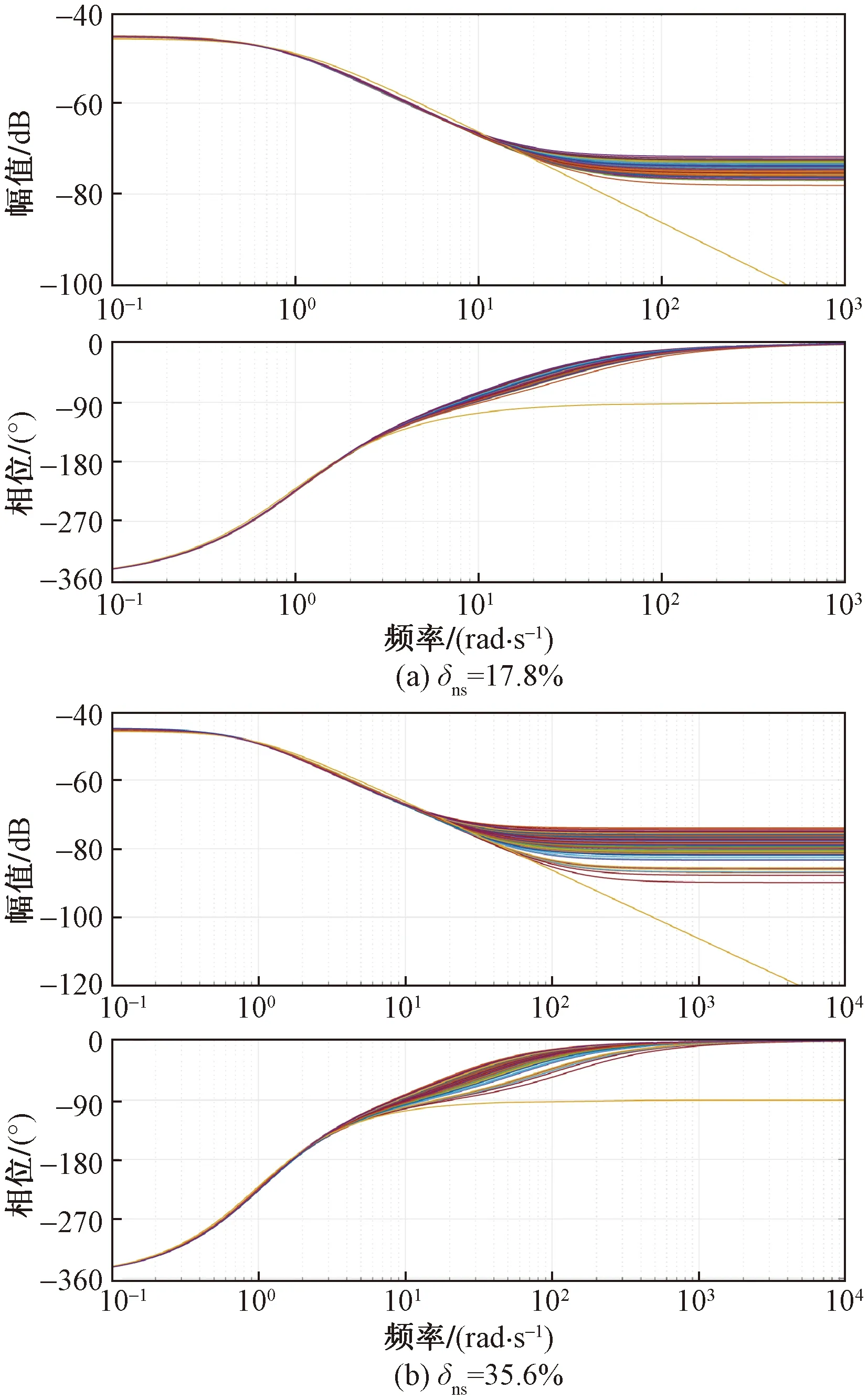
图4 δns=17.8%、35.6%估计模型的bode图

图5 δns=17.8%、35.6%特征值变化

当噪声的方差σ2=0.382，信噪比δns=35.6%时，在低频段范围内，辨识模型的bode曲线与原系统的bode曲线仍能保持基本重合。当信噪比增大时，在低频段范围内，该系统的辨识模型仍然能够良好地跟踪到原采样系统的变化。

当信噪比为δns=17.8%时，状态转移矩阵A的特征值的估计分布如图5(a)所示。当信噪比为δns=35.6%时，状态转移矩阵A的特征值的估计分布图如图5(b)所示。原系统状态转移矩阵A的特征值为{0.947 7±0.082 3i}。从图5可以看出，当信噪比不同的情况下，本文方法给出的特征值估计可以几乎重合实际系统的真实特征值。因此，本文算法具有一定的鲁棒性，能够很好地估计模型参数。

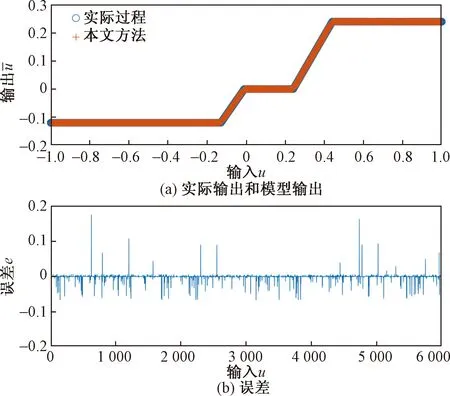
图6 静态非线性模糊神经模型的辨识结果

3.2 仿真实例2

为了进一步验证本文方法的有效性，考虑更加复杂的一类非线性过程：

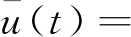
(31)

从图7可以看出，估计模型的奇异值在第一、第二阶时最大，其余都近乎为0。故将模型阶数选为2阶。为了避免实验结果的偶然性，以不同的噪声序列进行100次蒙特-卡罗实验。实验结果如图8、图9所示。

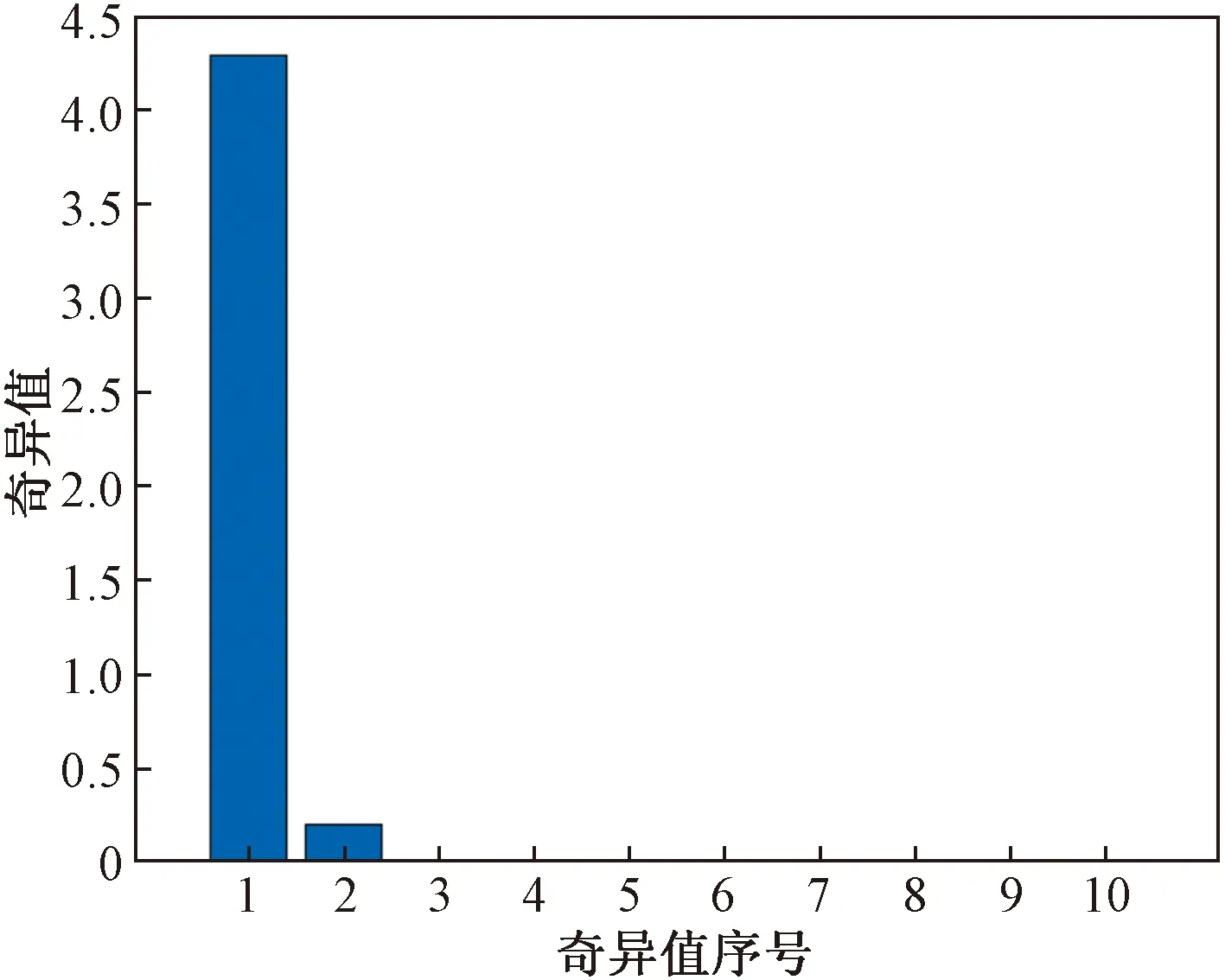
图7 估计模型奇异值的变化

当信噪比δns=14.53%时，状态转移矩阵A的特征值的估计分布如图9(a)所示。当信噪比为δns=29.06%时，状态转移矩阵A的特征值的估计分布图如图9(b)所示。原系统状态转移矩阵A的特征值为{0.947 7±0.082 3i}。从图9可以看出，当信噪比不同的情况下，本文方法给出的特征值估计可以几乎重合真实系统的特征值。因此，本文算法具有一定的鲁棒性，能够很好地估计模型参数。

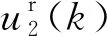
图8给出了不同噪信比下的状态空间模型辨识结果。从图8可以看出，当噪声的方差σ2=0.062，信噪比δns=14.53%时，在低频段范围内，辨识模型的bode曲线与原系统的bode曲线基本重合。当噪声的方差σ2=0.382，信噪比δns=29.06%时，在低频段范围内，辨识模型的bode曲线与原系统的bode曲线仍能保持基本重合。所以，当信噪比增大时，在低频段范围内，该系统的辨识模型仍然能够良好地跟踪到原采样系统的变化。

4 结论

通过融合模糊神经和子空间算法，提出了一种非线性采样系统的状态空间Hammerstein模型的辨识方法。先利用组合信号源解耦静态非线性模块和动态线性模块，以简化辨识过程；再采用模糊神经模型，能够很好地拟合非线性模块；最后利用子空间方法，状态空间方程系数矩阵可以简单、快捷地估计出来，使系统鲁棒性更好。两个仿真结果均验证了基于组合信号源的非线性子空间辨识方法的有效性。对于多变量的非线性采样系统，如何采用组合信号源的方式去解耦静态非线性模块和动态线性模块，再对其分别进行辨识，是今后的主要研究工作。